【高阶数据结构学习笔记】高阶数据结构之B树B+树B*树

【高阶数据结构学习笔记】高阶数据结构之B树B+树B*树

🔥个人主页：大白的编程日记

🔥专栏：高阶数据结构学习笔记

---

前言

哈喽，各位小伙伴大家好!上期我们讲了Linux基本指令及其分析(一) 今天我们讲的是Linux基本指令及其分析(二)。话不多说，我们进入正题！向大厂冲锋！

1. 常见的搜索结构

种类	数据格式	时间复杂度
顺序查找	无要求	O(N)
二分查找	有序	O($log_2 N$)
二叉搜索树	无要求	O(N)
二叉平衡树(AVL树和红黑树)	无要求	O($log_2 N$)
哈希	无要求	O(1)

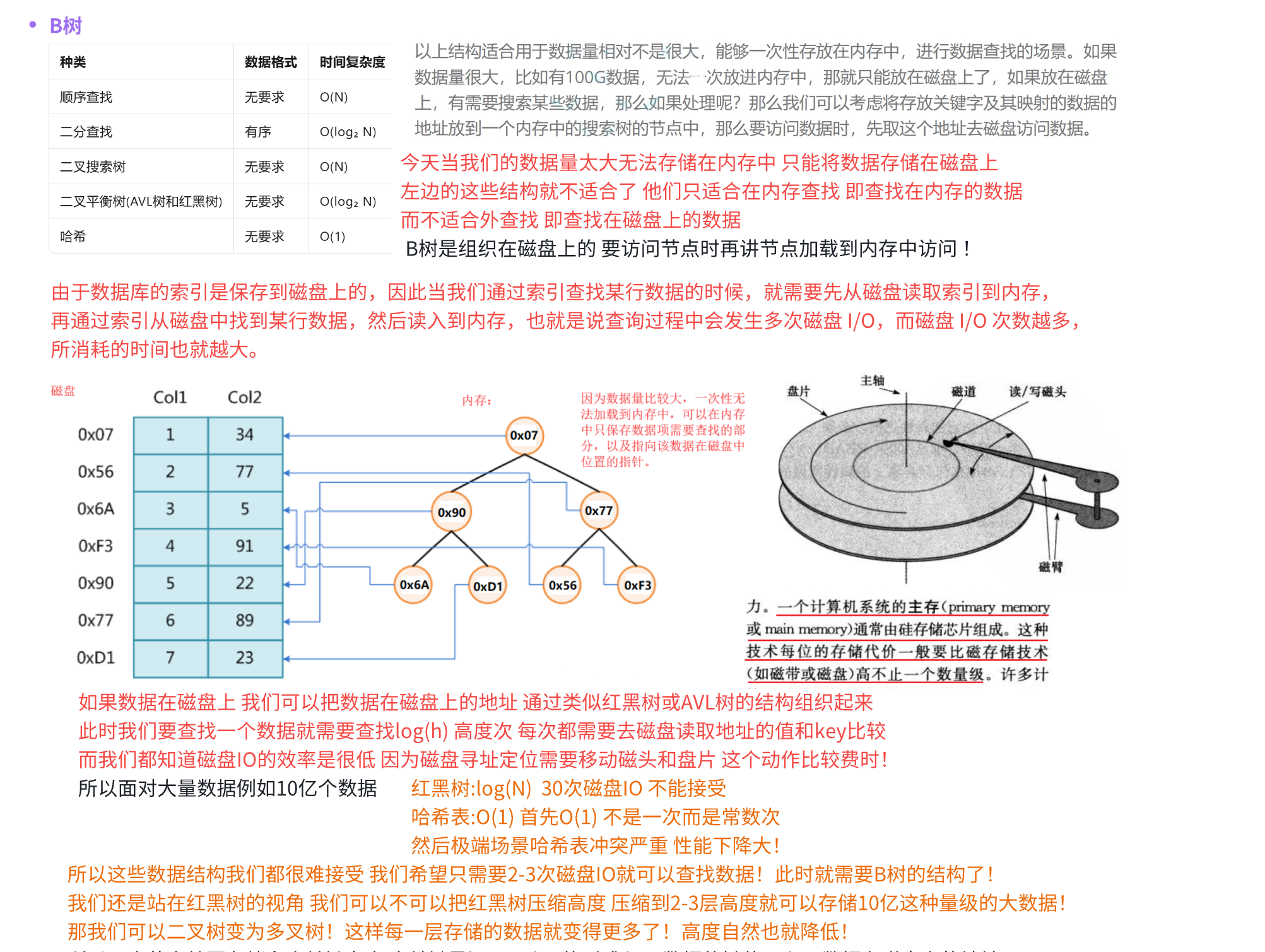
以上结构适合用于数据量相对不是很大，能够一次性存放在内存中，进行数据查找的场景。如果数据量很大，比如有100G数据，无法一次放进内存中，那就只能放在磁盘上了，如果放在磁盘上，有需要搜索某些数据，那么如果处理呢？那么我们可以考虑将存放关键字及其映射的数据的地址放到一个内存中的搜索树的节点中，那么要访问数据时，先取这个地址去磁盘访问数据。

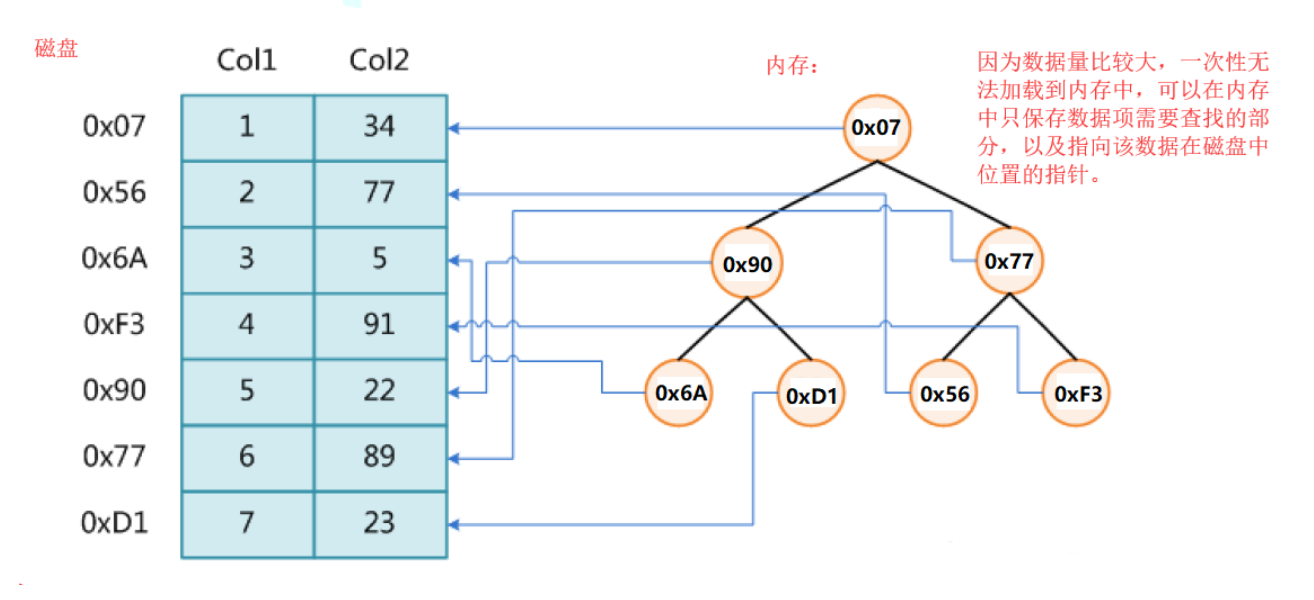
磁盘

以下内容来源《算法导论》

1.1 辅存上的数据结构

计算机系统利用各种技术来提供存储能力。一个计算机系统的主存（primary memory 或 main memory）通常由硅存储芯片组成。这种技术每位的存储代价一般要比磁存储技术（如磁带或磁盘）高不止一个数量级。许多计算机系统还有基于磁盘的辅存（secondary storage）；这种辅存的容量通常要比主存的容量高出至少两个数量级。

图18-2是一个典型的磁盘驱动器。驱动

图18-2 一个典型的磁盘驱动器。它包括了一个或多个绕主轴旋转的盘片（这里画出的是两个）。每个盘片通过磁臂末端的磁头来读写。这些磁臂围绕着一个共同的旋转轴旋转。当读/写磁头静止时，由它下方经过的磁盘表面就是一个磁道

器由一个或多个盘片(platter)组成，它们以一个固定的速度绕着一个共同的主轴(spindle)旋转。每个盘的表面覆盖着一层可磁化的物质。驱动器通过磁臂(arm)末尾的磁头(head)来读/写盘片。磁臂可以将磁头向主轴移近或移远。当一个给定的磁头处于静止时，它下面经过的磁盘表面称为一个磁道(track)。多个盘片增加的仅仅是磁盘驱动器的容量，而不影响性能。

尽管磁盘比主存便宜并且具有更多的容量，但是它们比主存慢很多，因为它们有机械运动的部分。磁盘有两个机械运动的部分：盘片旋转和磁臂移动。在撰写本书时，商用磁盘的旋转速度是 $5400\sim 15000$ 转/分钟(RPM)。通常看到的15000RPM的速度是用于服务器级的驱动器上，7200RPM的速度用于台式机的驱动器上，5400RPM的速度用于笔记本的驱动器上。尽管7200RPM看上去很快，但是旋转一圈需要8.33ms，比硅存储的常见存取时间50ns要高出5个数量级。也就是说，如果不得不等待一个磁盘旋转完整的一圈，让一个特定的项到达读/写磁头下方，在这个时间内，我们可能存取主存超过100000次。平均来讲，只需等待半圈，但硅存储存取时间和磁盘存储存取时间的差距仍然是巨大的。移动磁臂也要耗费时间。在撰写本书时，商用磁盘的平均存取时间在 $8\sim 11\mathrm{ms}$ 范围内。

为了摊还机械移动所花费的等待时间，磁盘会一次存取多个数据项而不是一个。信息被分为一系列相等大小的在柱面内连续出现的位页面（page），并且每个磁盘读或写一个或多个完整的页面。对于一个典型的磁盘来说，一页的长度可能为 $2^{11}\sim 2^{14}$ 字节。一旦读/写磁头正确定位，并且盘片已经旋转到所要页面的开头位置，对磁盘的读或写就完全电子化了（除了磁盘的旋转外），磁盘能够快速地读或写大量的数据。

通常，定位到一页信息并将其从磁盘里读出的时间要比对读出信息进行检查的时间要长得多。因此，本章将对运行时间的两个主要组成成分分别加以考虑：

1.2 使用平衡二叉树搜索树的缺陷：

平衡二叉树搜索树的高度是logN，这个查找次数在内存中是很快的。但是当数据都在磁盘中时，访问磁盘速度很慢，在数据量很大时，logN次的磁盘访问，是一个难以接受的结果。

1.3使用哈希表的缺陷：

哈希表的效率很高是O(1)，但是一些极端场景下某个位置冲突很多，导致访问次数剧增，也是难以接受的。

那如何加速对数据的访问呢？

1. 提高IO的速度(SSD相比传统机械硬盘快了不少，但是还是没有得到本质性的提升)
2. 降低树的高度—多叉树平衡树
   

2. B树概念

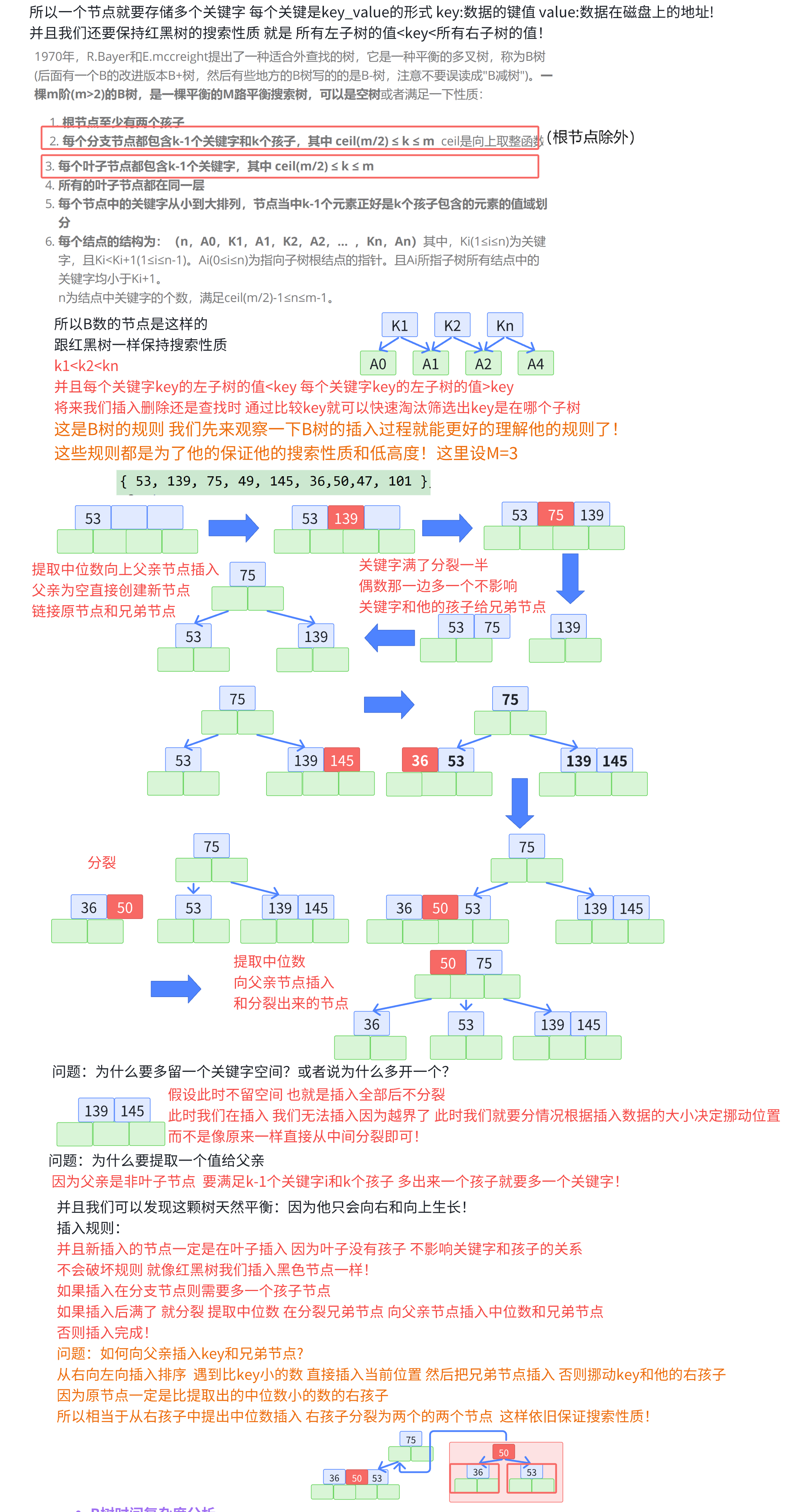
1970年，R.Bayer和E.mccreight提出了一种适合外查找的树，它是一种平衡的多叉树，称为B树(后面有一个B的改进版本B+树，然后有些地方的B树写的的是B-树，注意不要误读成"B减树")。一棵m阶(m>2)的B树，是一棵平衡的M路平衡搜索树，可以是空树或者满足一下性质：

1. 根节点至少有两个孩子

2. 每个分支节点都包含k-1个关键字和k个孩子，其中ceil(m/2) ≤ k ≤ mceil是向上取整函数

3. 每个叶子节点都包含k-1个关键字，其中ceil(m/2) ≤ k ≤ m

4. 所有的叶子节点都在同一层

5. 每个节点中的关键字从小到大排列，节点当中k-1个元素正好是k个孩子包含的元素的值域划分

6. 每个结点的结构为：（n，A0，K1，A1，K2，A2，...，Kn，An）其中，Ki(1≤i≤n)为关键字，且Ki<Ki+1(1≤i≤n-1)。Ai(0≤i≤n)为指向子树根结点的指针。且Ai所指子树所有结点中的关键字均小于Ki+1。

n为结点中关键字的个数，满足ceil(m/2)-1≤n≤m-1。

2.1 B-树的插入分析

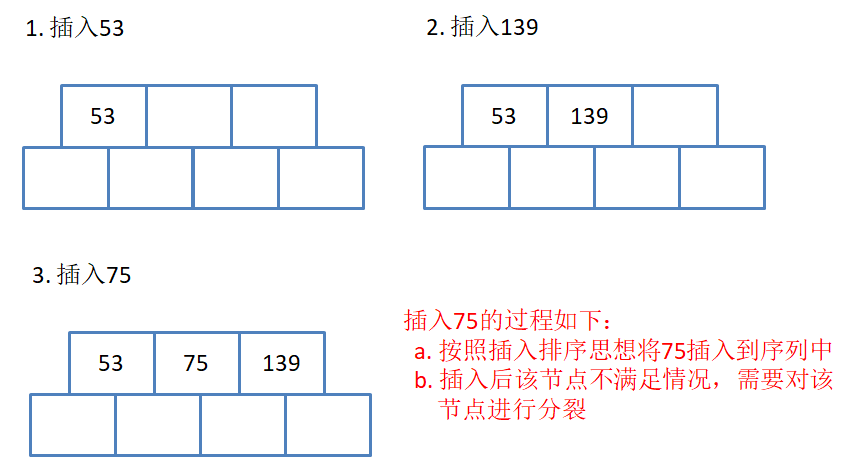
为了简单起见，假设 $M=3$ 。即三叉树，每个节点中存储两个数据，两个数据可以将区间分割成三个部分，因此节点应该有三个孩子，为了后续实现简单期间，节点的结构如下：

注意：孩子永远比数据多一个。

用序列{53, 139, 75, 49, 145, 36, 101}构建B树的过程如下：

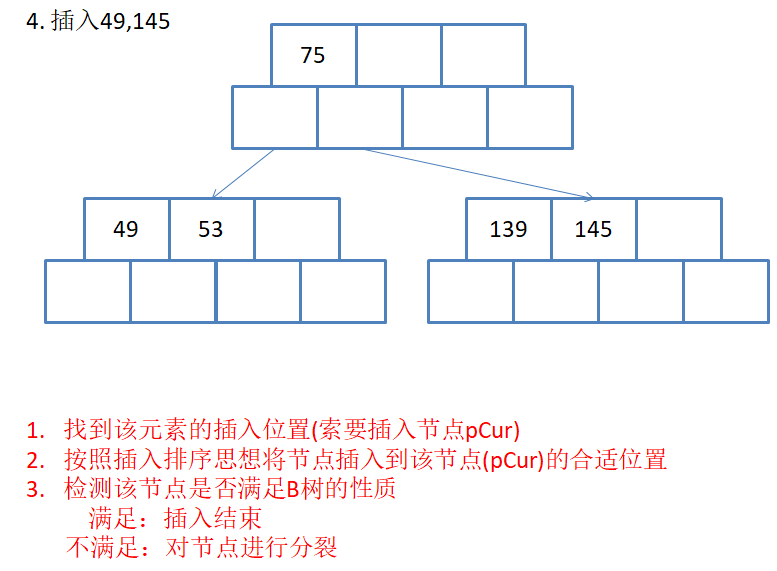
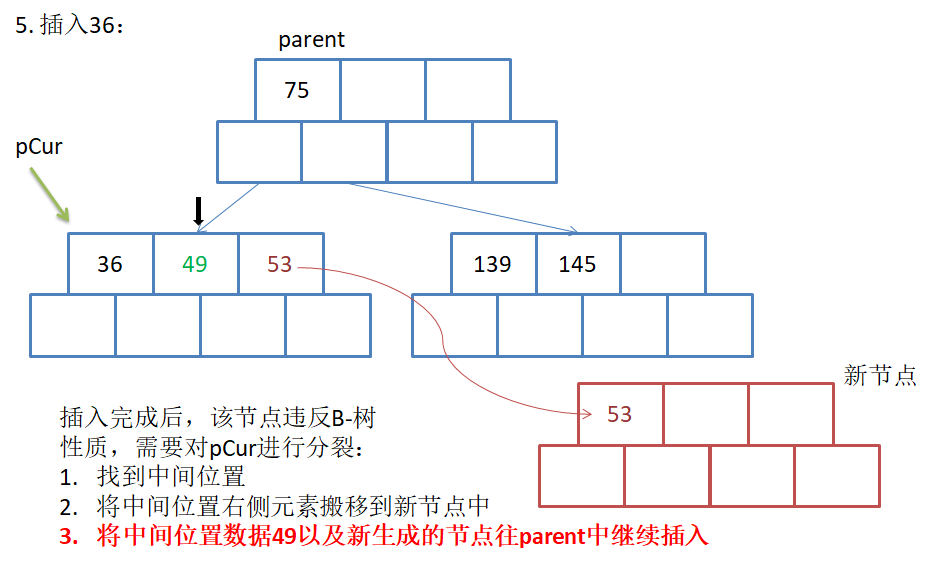
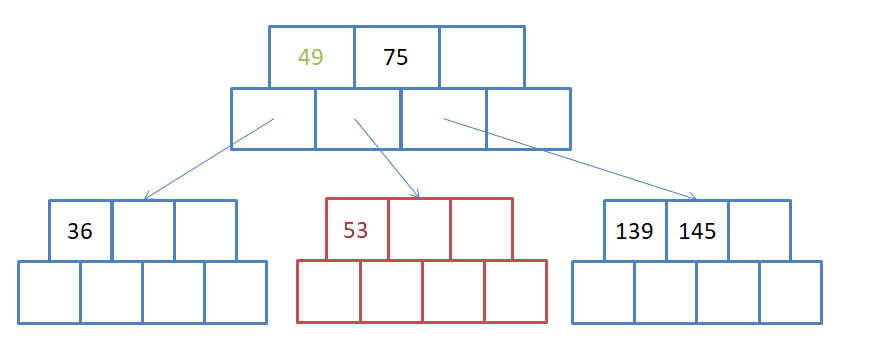
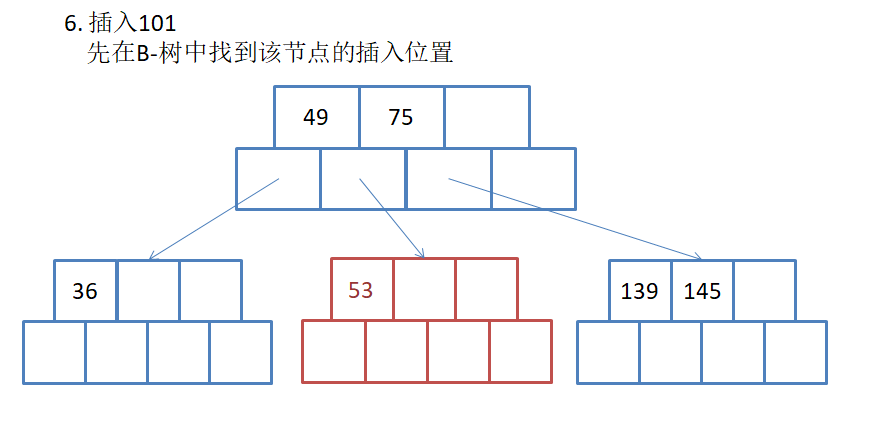
// 参数：key为待查找的元素
// 返回值：PNode代表找到的节点，int为该元素在该节点中的位置
pair<PNode, int> Find(const K& key)
{
// 从根节点的位置开始查找PNode pCur = _pRoot;PNode pParent = NULL;size_t i = 0;
// 节点存在while(pCur){i = 0;// 在该节点的值域中查找while(i < pCur->_size){// 找到返回if(key == pCur->_keys[i])return pair<PNode, int>(pCur, i);else if(key < pCur->_keys[i])  // 该元素可能在i的左边的孩子节点中break;elsei++;  // 继续向右查找}// 在pCur中没有找到，到pCur节点的第i个孩子中查找pParent = pCur;pCur = pCur->_pSub[i];}
// 没有找到return pair<PNode, int>(pParent, -1);
}

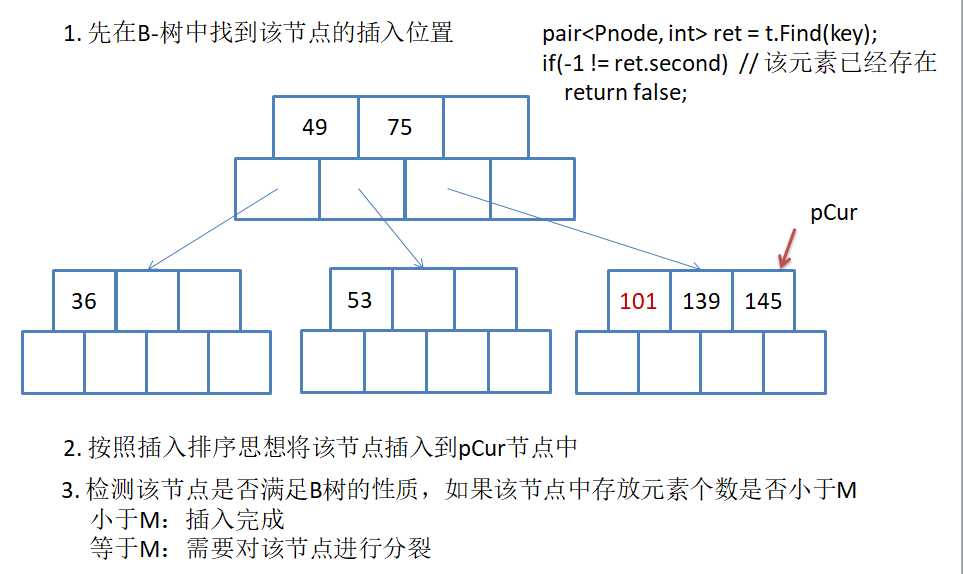
2.2 插入过程总结：

1. 如果树为空，直接插入新节点中，该节点为树的根节点

2. 树非空，找待插入元素在树中的插入位置(注意：找到的插入节点位置一定在叶子节点中)

3. 检测是否找到插入位置(假设树中的key唯一，即该元素已经存在时则不插入)

4. 按照插入排序的思想将该元素插入到找到的节点中

5. 检测该节点是否满足B- 树的性质：即该节点中的元素个数是否等于M, 如果小于则满足

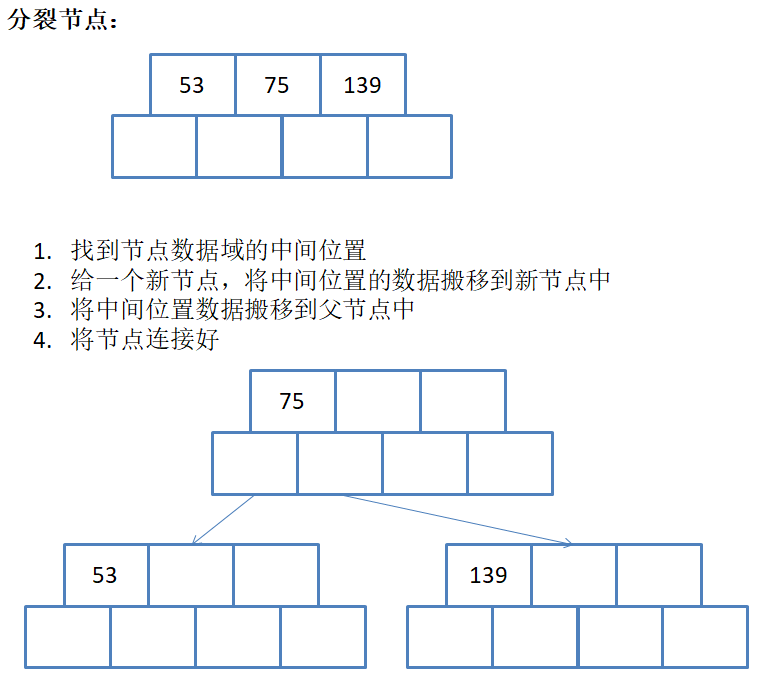
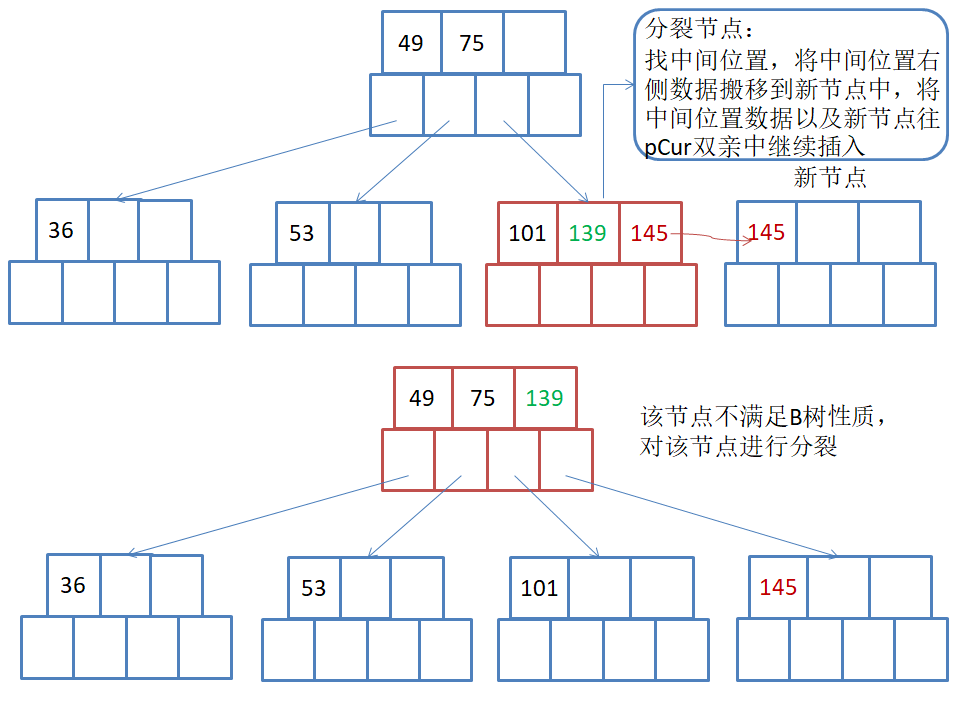
6. 如果插入后节点不满足B树的性质，需要对该节点进行分裂：

   • 申请新节点
   • 找到该节点的中间位置
   • 将该节点中间位置右侧的元素以及其孩子搬移到新节点中
   • 将中间位置元素以及新节点往该节点的双亲节点中插入，即继续4

7. 如果向上已经分裂到根节点的位置，插入结束

3. B-树的插入实现

3.1 B-树的节点设计

// M叉树：即一个节点最多有M个孩子，M-1个数据域  
// 为实现简单期间，数据域与孩子与多增加一个（原因参见上文对插入过程的分析）  
template<class K, int M = 3>  
struct BTreeNode  
{  K keys[M]; // 存放元素  BTreeNode<K, M>* _pSub[M+1]; // 存放孩子节点，注意：孩子比数据多一个  BTreeNode<K, M>* _pParent; // 在分裂节点后可能需要继续向上插入，为实现简单增加parent域  size_t size; // 节点中有效元素的个数  BTreeNode()  : _pParent(NULL)  , _size(0)  {  for(size_t i = 0; i <= M; ++i)  _pSub[i] = NULL;  }  
};

3.2 插入key的过程

按照插入排序的思想插入key，注意：在插入key的同时，可能还要插入新分裂出来的节点。

void _InsertKey(PNode pCur, const K& key, PNode pSub)  
{  
// 按照插入排序思想插入key  
int end = pCur->_size - 1;  
while (end >= 0)  
{  if (key < pCur->_keys[end])  {  // 将该位置元素以及其右侧孩子往右搬移一个位置  pCur->_keys[end + 1] = pCur->_keys[end];  pCur->_pSub[end + 2] = pCur->_pSub[end + 1];  end--;  }  else  break;  
}  // 插入key以及新分裂出的节点  pCur->_keys[end + 1] = key;  pCur->_pSub[end + 2] = pSub;  // 更新节点的双亲  if(pSub)  pSub->_pParent = pCur;  
pCur->_size++;

3.3 B-树的插入实现

bool Insert(const K& key)
{//第一个节点if (_root == nullptr){Node* root = new Node();root->_keys[0] = key;root->_n = 1;_root = root;return true;}auto ret = Find(key);//如果存在该值直接返回if (ret.second >=0 ){return false;}// 循环每次往cur插入 newkey和childNode* parent = ret.first;K newKey = key;Node* child = nullptr;while (1){//向叶子节点插入InsertKey(parent, newKey, child);if (parent->_n < M){return true;}Node* brother = new Node;size_t j = 0;size_t mid = M / 2;//分裂[mid+1,M-1]的值给兄弟节点for (int i = mid+1;i < M; i++){//分裂key和他的左孩子节点brother->_keys[j] = parent->_keys[i];brother->_subs[j] = parent->_subs[i];//更新节点的父亲if (parent->_subs[i]){parent->_subs[i]->_parent = parent;}//清空原节点的key和孩子节点parent->_keys[i] = K();parent->_subs[i]=nullptr;j++;}//分裂最右孩子节点brother->_subs[j] = parent->_subs[M];if (parent->_subs[M]){parent->_subs[M]->_parent =brother;}//更新数目parent->_subs[M] = nullptr;brother->_n = j;parent->_n -= (brother->_n+1);K midkey = parent->_keys[mid];parent->_keys[mid] = K();//原节点是根节点直接连接左右节点if (parent->_parent == nullptr){Node* root = new Node;root->_keys[0] = midkey;root->_subs[0] = parent;root->_subs[1] = brother;parent->_parent = root;brother->_parent = root;root->_n = 1;_root=root;break;}//向上一级父亲节点递归插入else{parent = parent->_parent;newKey = midkey;child = brother;}}return true;
}

3.4 B-树的简单验证

对B树进行中序遍历，如果能得到一个有序的序列，说明插入正确。

void _InOrder(PNode pRoot)
{if(NULL == pRoot)return;for(size_t i = 0; i < pRoot->_size; ++i){_InOrder(pRoot->_pSub[i]);cout<<pRoot->_keys[i]<<" ";}_InOrder(pRoot->_pSub[pRoot->_size]);
}

3.5 B-树的性能分析

对于一棵节点为N度为M的B-树,查找和插入需要$logM-1N$_{$/log{M/2}N$次比较,这个很好证明:对于度为M的B-树,每一个节点的子节点个数为M/2}(M-1)之间,因此树的高度应该在要$logM-1N$和$/logM/2N$之间,在定位到该节点后,再采用二分查找的方式可以很快的定位到该元素。

B-树的效率是很高的,对于N = 62*100000000个节点,如果度M为1024,则 l o g { M / 2 } N log_{\{M/2\}}N log{M/2}​N <= 4,即在620亿个元素中,如果这棵树的度为1024,则需要小于4次即可定位到该节点,然后利用二分查找可以快速定位到该元素,大大减少了读取磁盘的次数。

4.6 B-树的删除

学习B树的插入足够帮助我们理解B树的特性了，如果对删除有兴趣的同学们参考《算法导论》–伪代码和《数据结构-般人昆》–C++实现代码。

4. B+树和B*树

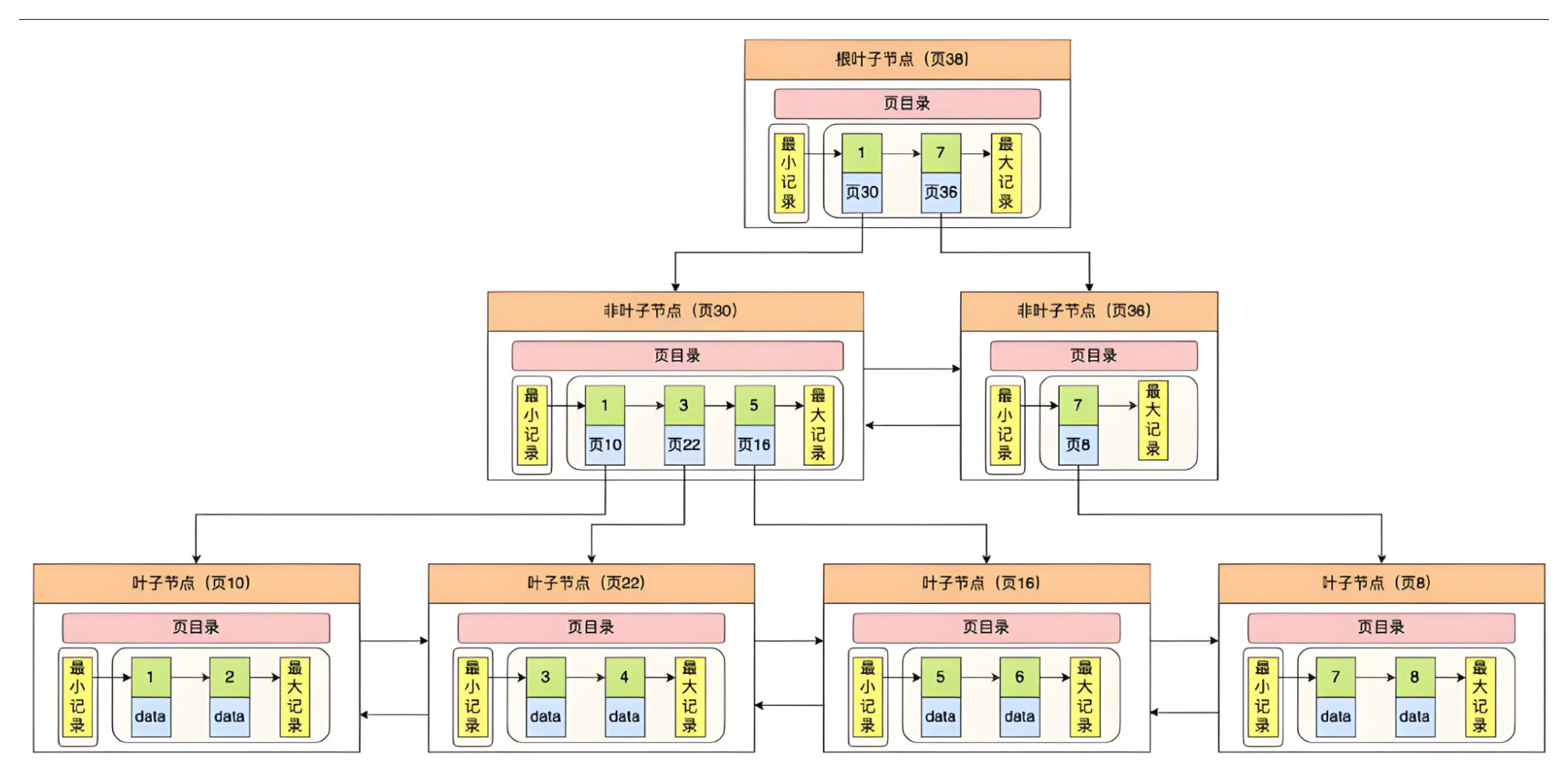
4.1 B+树

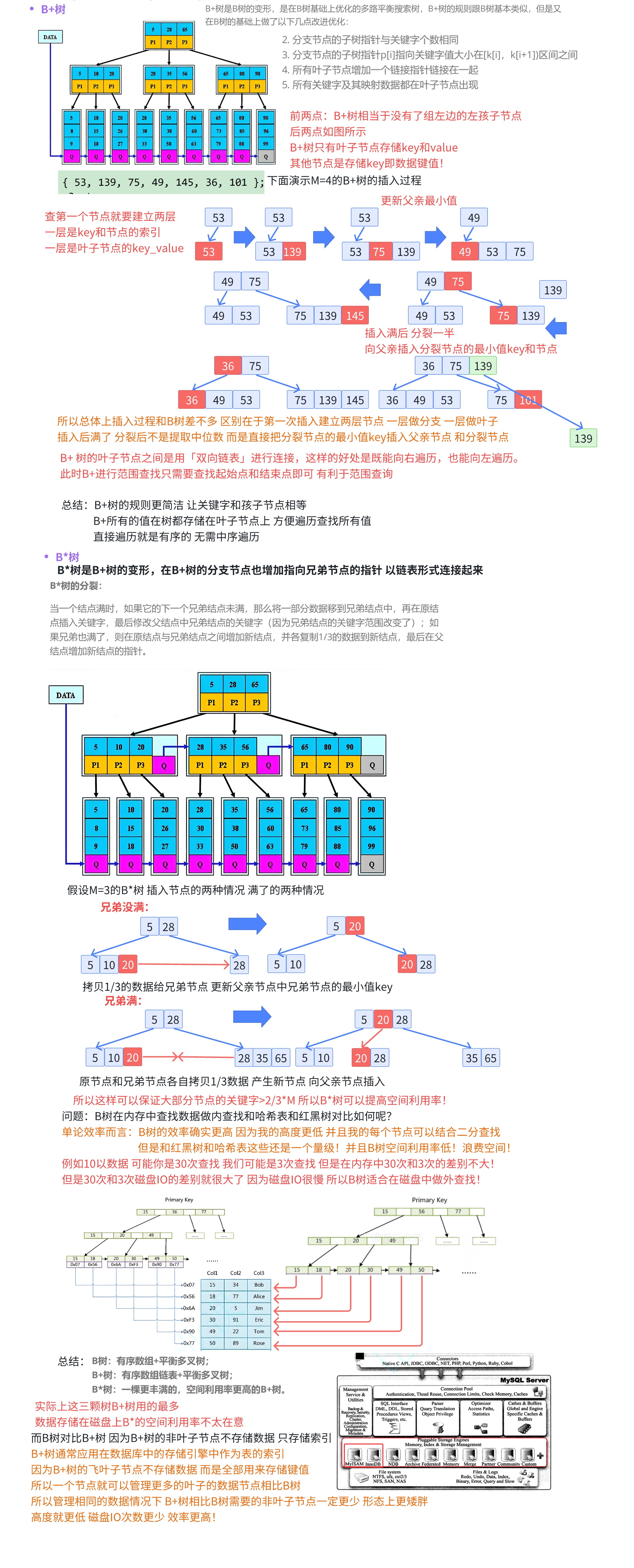
B+树是B树的变形，是在B树基础上优化的多路平衡搜索树，B+树的规则跟B树基本类似，但是又在B树的基础上做了以下几点改进优化：

2. 分支节点的子树指针与关键字个数相同
3. 分支节点的子树指针p[i]指向关键字值大小在[k[i], k[i+1])区间之间
4. 所有叶子节点增加一个链接指针链接在一起
5. 所有关键字及其映射数据都在叶子节点出现

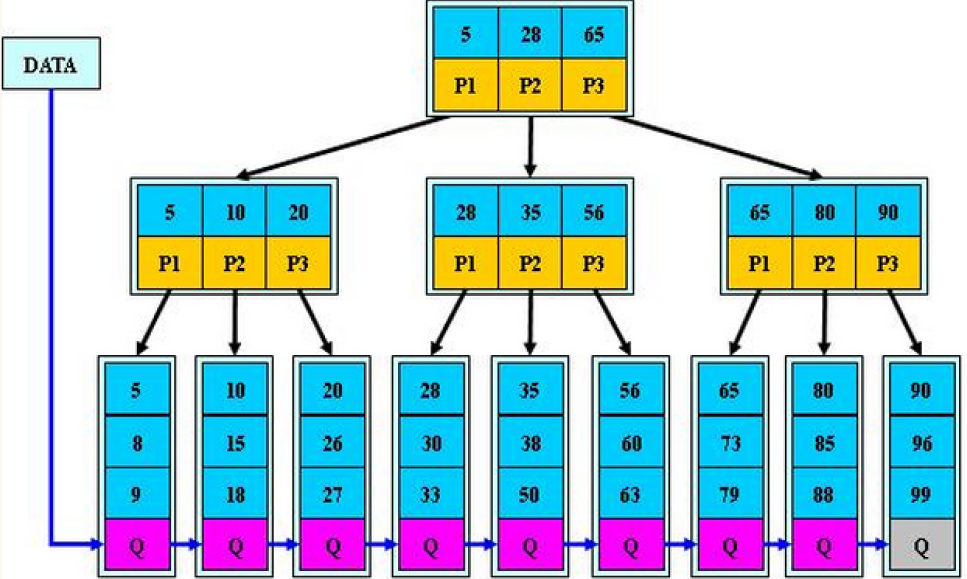
4.2 B+树的特性：

1. 所有关键字都出现在叶子节点的链表中，且链表中的节点都是有序的。
2. 不可能在分支节点中命中。
3. 分支节点相当于是叶子节点的索引，叶子节点才是存储数据的数据层。

4.2 B*树

B*树是B+树的变形，在B+树的非根和非叶子节点再增加指向兄弟节点的指针。

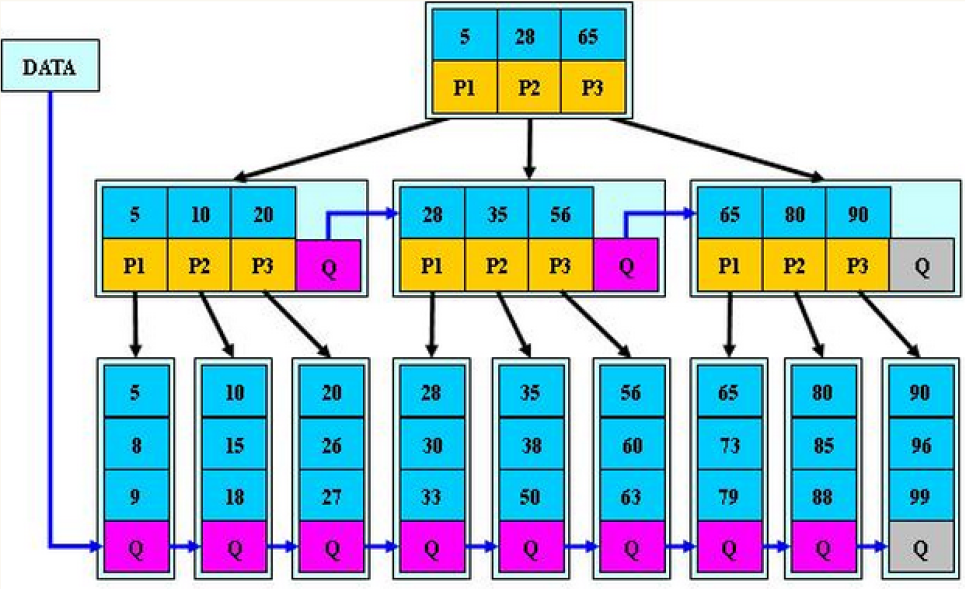
4.3 B+树的分裂:

当一个结点满时，分配一个新的结点，并将原结点中1/2的数据复制到新结点，最后在父结点中增加新结点的指针；B+树的分裂只影响原结点和父结点，而不会影响兄弟结点，所以它不需要指向兄弟的指针。

4.4 B*树的分裂:

当一个结点满时，如果它的下一个兄弟结点未满，那么将一部分数据移到兄弟结点中，再在原结点插入关键字，最后修改父结点中兄弟结点的关键字（因为兄弟结点的关键字范围改变了）；如果兄弟也满了，则在原结点与兄弟结点之间增加新结点，并各复制1/3的数据到新结点，最后在父结点增加新结点的指针。

所以，B*树分配新结点的概率比B+树要低，空间使用率更高；

4.5总结

通过以上介绍，大致将B树，B+树，B*树总结如下：

B树：有序数组+平衡多叉树；

B+树：有序数组链表+平衡多叉树；

B*树：一棵更丰满的，空间利用率更高的B+树。

5. B-树的应用

5.1索引

B-树最常见的应用就是用来做索引。索引通俗的说就是为了方便用户快速找到所寻之物，比如：书籍目录可以让读者快速找到相关信息，hao123网页导航网站，为了让用户能够快速的找到有价值的分类网站，本质上就是互联网页面中的索引结构。

MySQL官方对索引的定义为：索引(index)是帮助MySQL高效获取数据的数据结构，简单来说：索引就是数据结构。

当数据量很大时，为了能够方便管理数据，提高数据查询的效率，一般都会选择将数据保存到数据库，因此数据库不仅仅是帮助用户管理数据，而且数据库系统还维护着满足特定查找算法的数据结构，这些数据结构以某种方式引用数据，这样就可以在这些数据结构上实现高级查找算法，该数据结构就是索引。

5.2 MySQL索引简介

mysql是目前非常流行的开源关系型数据库，不仅是免费的，可靠性高，速度也比较快，而且拥有灵活的插件式存储引擎，如下：

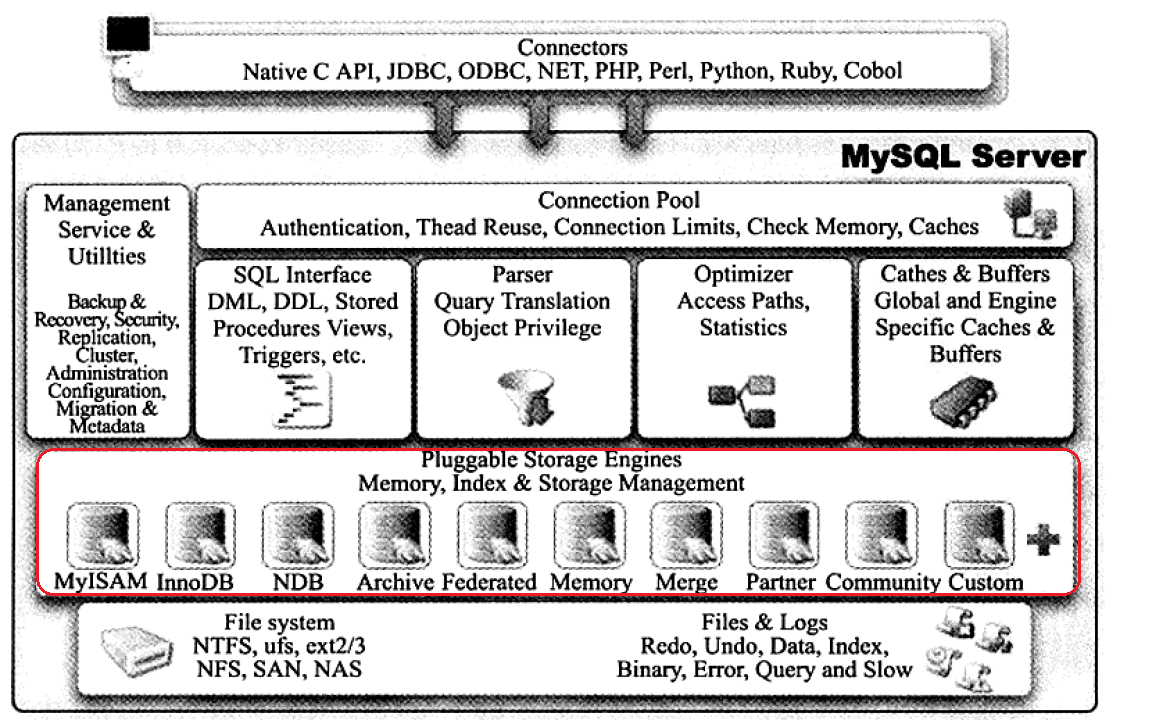
MySQL中索引属于存储引擎级别的概念，不同存储引擎对索引的实现方式是不同的。

5.2.1 MyISAM

MyISAM引擎是MySQL5.5.8版本之前默认的存储引擎，不支持事物，支持全文检索，使用B+Tree作为索引结构，叶节点的数据域存放的是数据记录的地址，其结构如下：

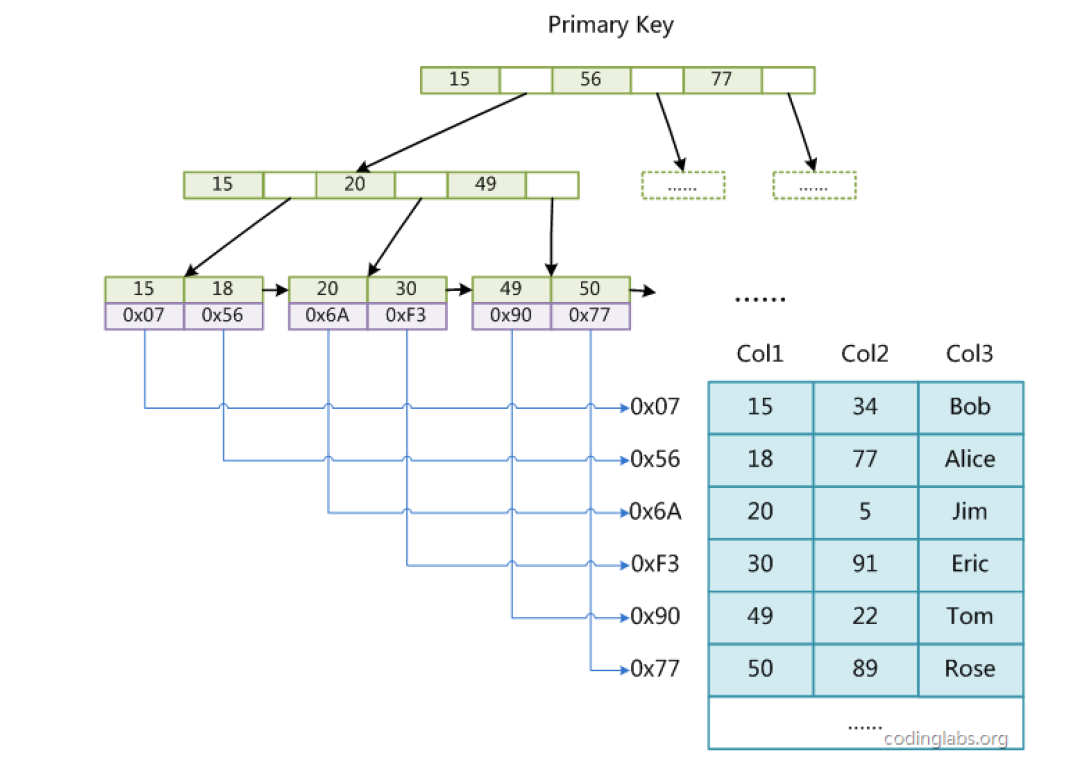
上图是以以Col1为主键，MyISAM的示意图，可以看出MyISAM的索引文件仅仅保存数据记录的地址。在MyISAM中，主索引和辅助索引（Secondary key）在结构上没有任何区别，只是主索引要求key是唯一的，而辅助索引的key可以重复。如果想在Col2上建立一个辅助索引，则此索引的结构如下图所示：

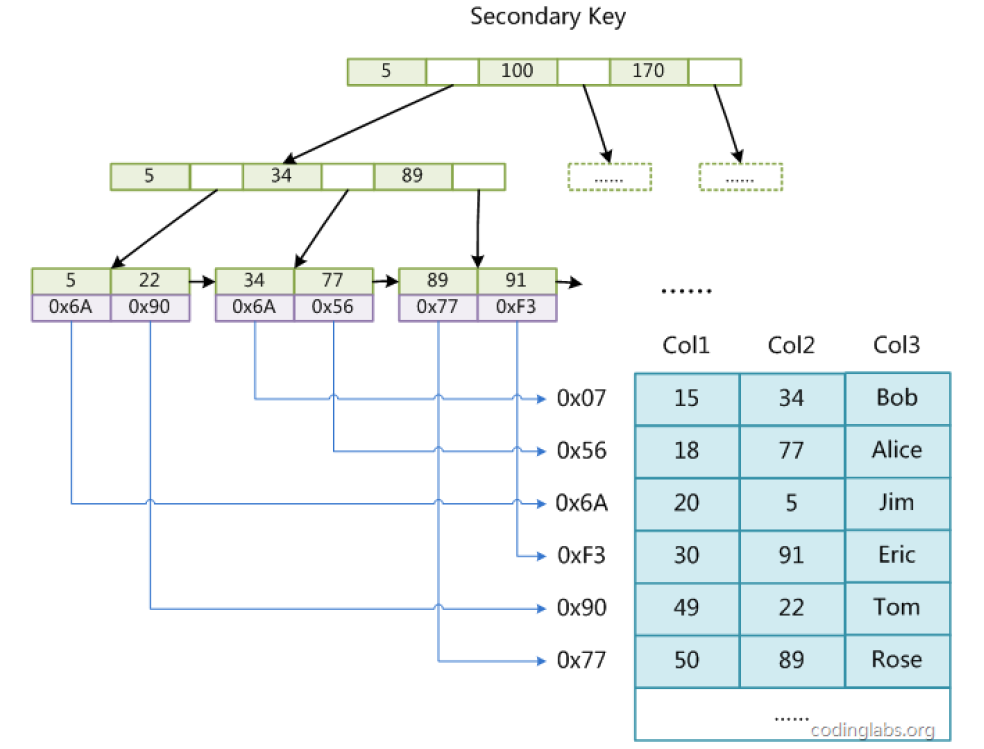
同样也是一棵B+Tree，data域保存数据记录的地址。因此，MyISAM中索引检索的算法为首先按照B+Tree搜索算法搜索索引，如果指定的Key存在，则取出其data域的值，然后以data域的值为地址，读取相应数据记录。MyISAM的索引方式也叫做“非聚集索引”的。

5.2.2 InnoDB

InnoDB存储引擎支持事务，其设计目标主要面向在线事务处理的应用，从MySQL数据库5.5.8版本开始，InnoDB存储引擎是默认的存储引擎。InnoDB支持B+树索引、全文索引、哈希索引。但InnoDB使用B+Tree作为索引结构时，具体实现方式却与MyISAM截然不同。

第一个区别是InnoDB的数据文件本身就是索引文件。MyISAM索引文件和数据文件是分离的，索引文件仅保存数据记录的地址。而InnoDB索引，表数据文件本身就是按B+Tree组织的一个索引结构，这棵树的叶节点data域保存了完整的数据记录。这个索引的key是数据表的主键，因此InnoDB表数据文件本身就是主索引。

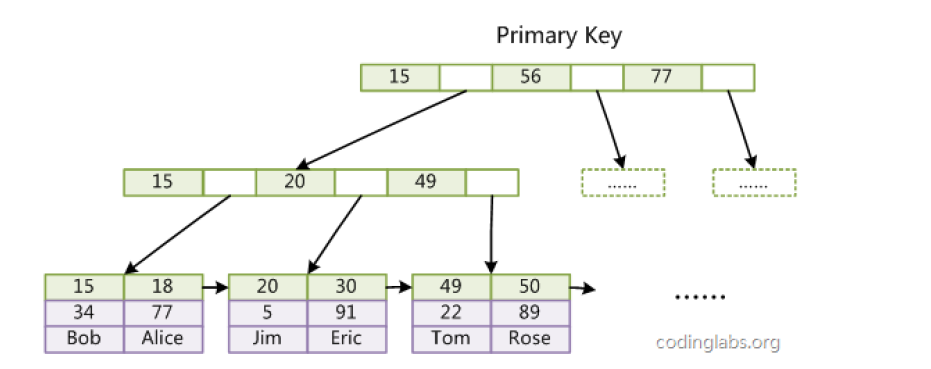
上图是InnoDB主索引（同时也是数据文件）的示意图，可以看到叶节点包含了完整的数据记录，这种索引叫做聚集索引。因为InnoDB的数据文件本身要按主键聚集，所以InnoDB要求表必须有主键（MyISAM可以没有），如果没有显式指定，则MySQL系统会自动选择一个可以唯一标识数据记录的列作为主键，如果不存在这种列，则MySQL自动为InnoDB表生成一个隐含字段作为主键，这个字段长度为6个字节，类型为长整型。

第二个区别是InnoDB的辅助索引data域存储相应记录主键的值而不是地址，所有辅助索引都引用主键作为data域。

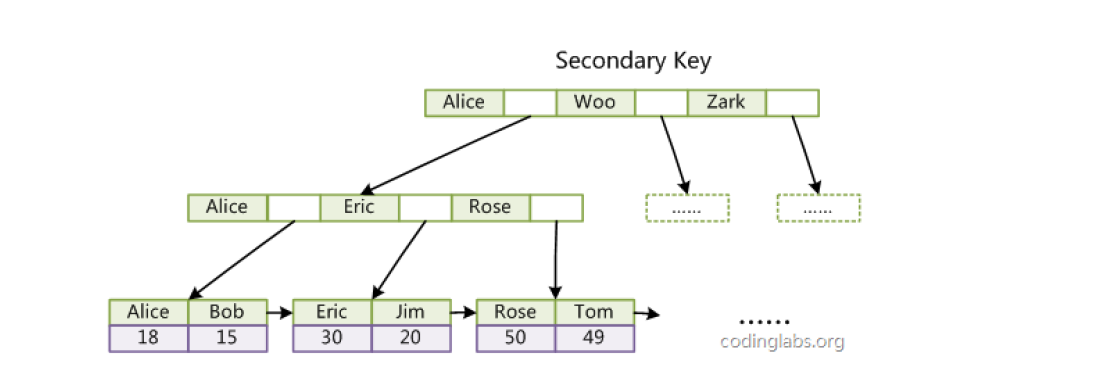
聚集索引这种实现方式使得按主键的搜索十分高效，但是辅助索引搜索需要检索两遍索引：首先检索辅助索引获得主键，然后用主键到主索引中检索获得记录。

后言

这就是B树B+树B*树。大家自己好好消化！今天就分享到这！ 感谢各位的耐心垂阅！咱们下期见！拜拜~