自然科学笔记-微积分

（2018年考研数学三（16））平面区域D是由 $x=0$, $y=\sqrt{3(1-x^2)}$, $y=\sqrt{3}x$ 围成的，求二重积分 $I=\underset{D}{\iint }{x}^2\mathrm{d}x\mathrm{d}y$。

% 通用方法，适用于各种方程
figure;
hold on;% 创建网格
[x, y] = meshgrid(linspace(-2, 2, 500));% 定义三个方程
f1 = sqrt(3) .* x - y; % 直线y = sqrt(3) * x
f2 = x.^2 + y.^2/3 - 1; % 椭圆: x^2/9 + y^2/4 = 1
f3 = x;             % 直线 x = 0% 绘制等高线（方程曲线）
contour(x, y, f1, [0 0], 'r-', 'LineWidth', 2);  % f1=0
contour(x, y, f2, [0 0], 'b-', 'LineWidth', 2);  % f2=0
contour(x, y, f3, [0 0], 'g-', 'LineWidth', 2);  % f3=0% 填充满足所有不等式的区域
% 例如：在f1以上、f2椭圆内、f3右侧的区域
region = (f1 <= 0) & (f2 <= 0) & (f3 >= 0);
contourf(x, y, double(region), [0.5 0.5], 'FaceColor', 'cyan', 'FaceAlpha', 0.3);grid on;
axis equal;
xlim([-2, 2]);
ylim([-2, 2]);
xlabel('x');
ylabel('y');
title('三个方程围成的区域');
legend('x^2+y^2=4', 'x^2/9+y^2/4=1', 'y=x^2', 'D');
legend on;hold off;

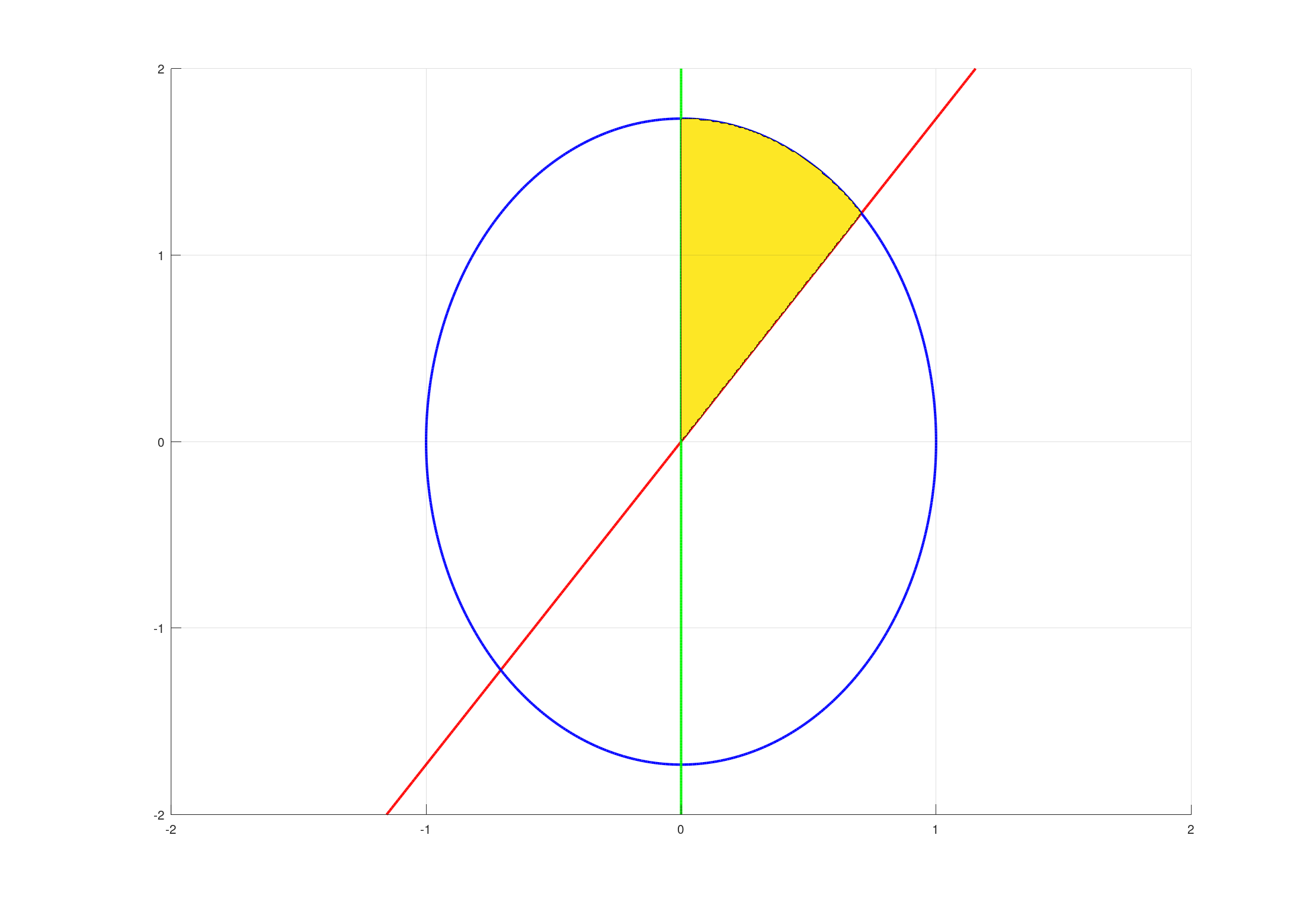
黄色部分是平面区域D。先对y积分，上下界是椭圆和直线方程。再对x积分，上下界是$0$到$\frac{\sqrt{2}}{2}$。

$\begin{array}{rl}I& ={\int }_0^{\frac{\sqrt{2}}{2}}\mathrm{d}x{\int }_{\sqrt{3}x}^{\sqrt{3(1-x^2)}}{x}^2\mathrm{d}y\\ & =\sqrt{3}({\int }_0^{\frac{\sqrt{2}}{2}}{x}^2\sqrt{1-x^2}\mathrm{d}x-{\int }_x^{\frac{\sqrt{2}}{2}}{x}^3\mathrm{d}x)\\ & =\sqrt{3}(I_1-I_2)\end{array}$

$\begin{array}{rl}{I}_1& \stackrel{x=\sin \theta }{=}{\int }_0^{\frac{\pi }{4}}{\sin }^2\theta {\cos }^2\theta \mathrm{d}\theta \\ & =\frac{1}{4}{\int }_0^{\frac{\pi }{4}}{\sin }^{2}2\theta \mathrm{d}\theta \\ & =\frac{1}{8}{\int }_0^{\frac{\pi }{4}}1-\cos 4\theta \mathrm{d}\theta \\ & ={\frac{1}{8}(\theta -\frac{1}{4}\sin 4\theta )|}_0^1\\ & =\frac{\pi }{32}\end{array}$

$\begin{array}{r}{I}_2={\frac{1}{4}{x}^4|}_0^{\frac{\sqrt{2}}{2}}=\frac{1}{16}\end{array}$

$\begin{array}{rl}I& =\sqrt{3}(I_1-I_2)\\ & =\sqrt{3}(\frac{\pi }{32}-\frac{1}{16})\\ & =\frac{\sqrt{3}(\pi -2)}{32}\end{array}$

---

计算二重积分$I={\int }_0^{\pi }{\int }_0^x\frac{\sin t}{\pi -t}\mathrm{d}t\mathrm{d}x$
$\begin{array}{rl}I& ={\int }_x^{\pi }{\int }_0^x\frac{\sin t}{\pi -t}\mathrm{d}t\mathrm{d}x\\ & ={\int }_0^{\pi }\mathrm{d}t{\int }_t^{\pi }\frac{\sin t}{\pi -t}\mathrm{d}x\\ & ={\int }_0^{\pi }\mathrm{d}t{\frac{\sin t}{\pi -t}x|}_t^{\pi }\\ & ={\int }_0^{\pi }\mathrm{d}t\frac{\sin t}{\pi -t}\times (\pi -t)\\ & ={\int }_0^{\pi }\sin t\mathrm{d}t\\ & ={-\cos t|}_0^{\pi }\\ & =2\end{array}$

---