【机器学习10】项目生命周期、偏斜类别评估、决策树

---

视频链接
吴恩达机器学习p83-p91

---

一 机器学习项目生命周期与部署

1.1 机器学习项目的完整生命周期

一个完整的机器学习项目包含四个主要阶段：

1. 项目范围定义 (Scope project)：此阶段的目标是定义项目。
2. 数据收集 (Collect data)：此阶段的目标是定义数据并进行收集。
3. 模型训练 (Train model)：此阶段包含训练、错误分析和迭代改进。这是一个循环过程，分析结果可能会指导重新收集数据或调整训练方法。
4. 生产部署 (Deploy in production)：此阶段的目标是部署、监控和维护整个系统。部署后，系统的表现可能会反馈至数据收集和模型训练阶段，形成一个更大的迭代循环。

1.2 模型部署与MLOps

部署是将训练好的模型投入实际应用的过程。一个常见的架构是：

• 客户端（如 Mobile app） 通过API调用，将输入数据 x（例如一段音频）发送到推理服务器（Inference server）。
• 推理服务器内嵌有训练好的机器学习模型（ML model）。
• 服务器接收输入 x，进行推理计算，并将预测结果 ŷ（例如文本转录）返回给客户端。

将模型部署到生产环境需要大量的软件工程工作，这一领域被称为MLOps（机器学习运维）。MLOps关注以下几方面：

• 确保预测的可靠性和效率。
• 系统的扩展性（Scaling）。
• 记录系统行为的日志（Logging）。
• 对系统状态进行监控（System monitoring）。
• 建立模型更新的流程（Model updates）。

二 偏斜类别下的模型评估

2.1 准确率的陷阱

当数据集中正负样本数量严重不均衡时，即存在偏斜类别（skewed classes），准确率（Accuracy）会成为一个有误导性的评估指标。

以一个罕见病分类为例：

• 一个分类器 f(x) 被训练用于检测疾病（y=1 代表患病）。
• 该分类器在测试集上达到了1%的错误率（即99%的准确率）。
• 然而，该疾病在人群中的真实患病率仅为0.5%。
• 一个不进行任何学习，只是简单地对所有人都预测y=0（健康）的程序，其错误率仅为0.5%，准确率高达99.5%。
• 这个结果（0.5%错误率）优于训练好的模型（1%错误率），这表明在偏斜类别问题中，高准确率并不能证明模型的有效性。

2.2 精确率与召回率

为解决偏斜类别下的评估问题，我们使用精确率（Precision）和召回率（Recall）。这些指标基于一个混淆矩阵（Confusion Matrix），该矩阵展示了模型的四种预测结果：

• 真正例 (True Positive, TP): 15
• 假正例 (False Positive, FP): 5
• 假负例 (False Negative, FN): 10
• 真负例 (True Negative, TN): 70

精确率 (Precision)：

• 问题：在所有被模型预测为y=1的病人中，真实患病的比例是多少？
• 公式：Precision = TP / (TP + FP)
• 计算：15 / (15 + 5) = 0.75

召回率 (Recall)：

• 问题：在所有真实患病的病人中，被模型成功检测出的比例是多少？
• 公式：Recall = TP / (TP + FN)
• 计算：15 / (15 + 10) = 0.6

2.3 指标的权衡

精确率和召回率之间存在权衡关系，这种关系可以通过调整分类器的**阈值（threshold）**来控制。

• 逻辑回归输出一个0到1之间的概率 f(x)。预测 y=1 的条件是 f(x) >= threshold。
• 高阈值（例如 0.99）：只有在模型极度确信时才预测 y=1。这会使精确率变高，召回率变低。
• 低阈值（例如 0.01）：只要模型对 y=1 存在一丝可能性就进行预测。这会使召回率变高，精确率变低。
• 图中的精确率-召回率曲线展示了随着阈值的变化，两个指标此消彼长的关系。

2.4 F1分数：综合评估指标

为了在只有一个数值的情况下比较不同算法的精确率和召回率表现，我们使用F1分数（F1 Score）。

• 简单的算术平均 (P+R)/2 是不可取的，因为它可能会给一个极端但无用的模型高分（如算法3）。
• F1分数是精确率（P）和召回率（R）的调和平均数（Harmonic Mean）。
• 公式：F1 Score = 2 * (P * R) / (P + R)
• F1分数要求P和R都比较高时，其值才会高。如表格所示，算法1的F1分数为0.444，而算法2的F1分数为0.175，这提供了一个明确的比较基准。

三 决策树模型详解

3.1 模型结构与预测

决策树是一种用于分类和回归的模型。以一个猫分类任务为例，输入数据 X 包含三个离散特征：耳朵形状（Ear shape）、脸部形状（Face shape）和是否有胡须（Whiskers）。输出标签 y 为1（是猫）或0（不是猫）。

决策树的结构包含：

• 根节点 (root node)：树的起点，代表第一个判断特征（例如 Ear shape）。
• 决策节点 (decision nodes)：树的中间节点，代表后续的判断特征。
• 叶节点 (leaf nodes)：树的终点，代表最终的分类结果（Cat 或 Not cat）。
  对一个新样本进行预测时，从根节点开始，根据其特征值沿树的分支向下，直至到达一个叶节点，该叶节点即为预测结果。

3.2 决策树学习的核心问题

对于同一份数据，可以构建出多种不同结构的决策树。

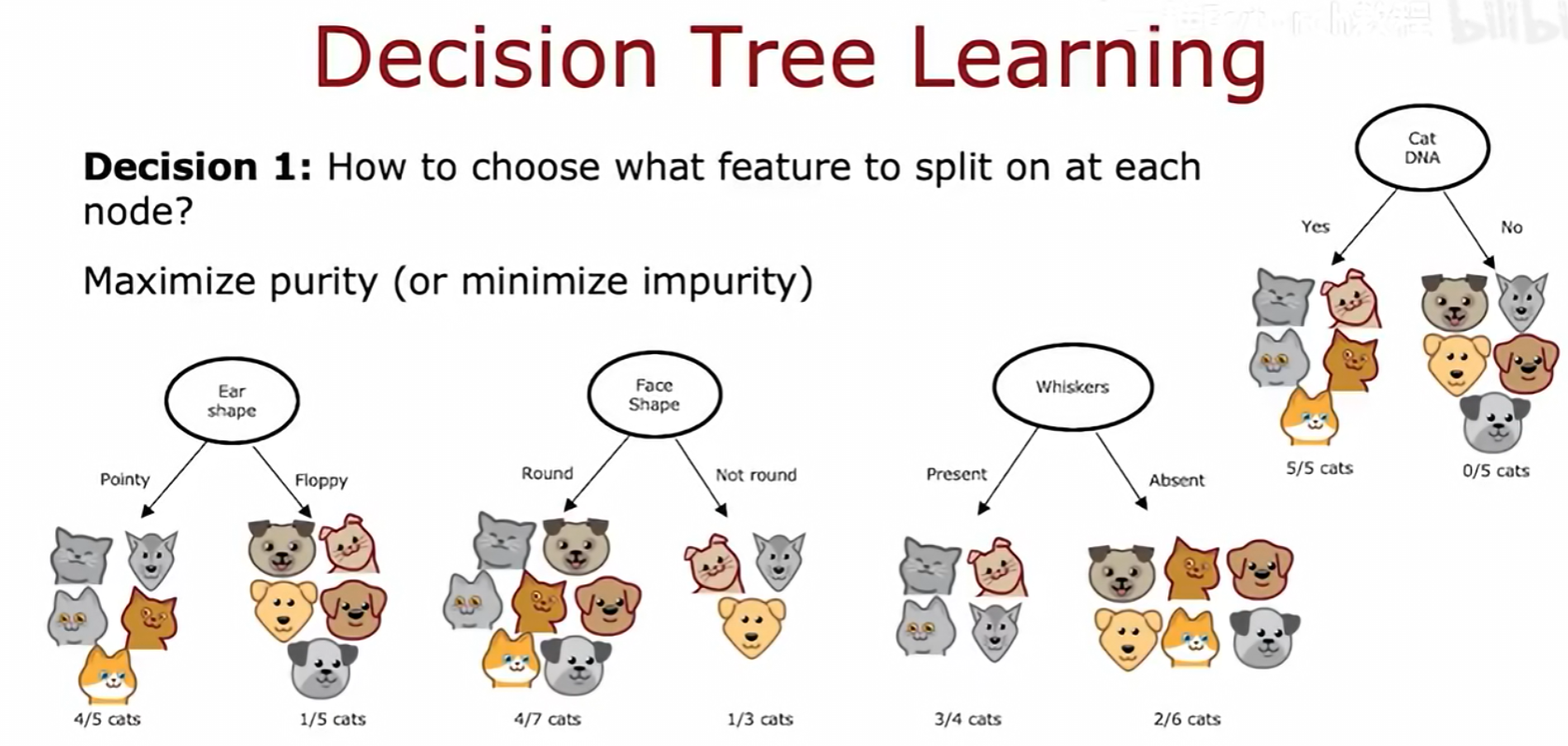
决策树学习算法主要解决两个核心问题：

1. 决策1：如何选择在每个节点上用于分裂的特征？
   • 原则：选择能最大化节点纯度（purity或最小化不纯度（impurity的特征。一个纯的节点意味着其包含的样本尽可能属于同一类别。
2. 决策2：何时停止分裂？
   • 停止条件：
     • 当一个节点已经是100%的同一类别时。
     • 当分裂会导致树超过预设的最大深度时。
     • 当分裂带来的纯度提升低于某个阈值时。
     • 当一个节点中的样本数量低于某个阈值时。

3.3 用熵衡量不纯度

熵（Entropy是用来衡量不纯度的常用指标。

• p₁ 被定义为节点中“是猫”的样本所占的比例。
• 熵函数 H(p₁) 的图像显示：
  • 当节点完全纯净时（p₁=0 或 p₁=1），熵 H(p₁)=0。
  • 当节点最不纯时（p₁=0.5），熵达到最大值 H(p₁)=1。
• 熵的计算公式 (针对二分类问题)：
  • H(p₁) = -p₁log₂(p₁) - p₀log₂(p₀)，其中 p₀ = 1 - p₁。
  • 根据约定，0 log₂(0) = 0。

3.4 信息增益：选择最佳分裂

信息增益（Information Gain是用来决定最佳分裂特征的指标。它衡量了进行一次分裂后，熵（不纯度）的减少量。

• 计算过程：
  1. 计算分裂前父节点的熵 H(p₁_root)。
  2. 计算分裂后所有子节点熵的加权平均值。权重 w 是每个子节点的样本数占父节点总样本数的比例。
  3. Information Gain = H(p₁_root) - (w_left * H(p₁_left) + w_right * H(p₁_right))
• 在图例中，初始节点熵为 H(0.5)=1。
  • 按“Ear shape”分裂，信息增益为 1 - [ (5/10)H(0.8) + (5/10)H(0.2) ] = 0.28。
  • 按“Face Shape”分裂，信息增益为 0.03。
  • 按“Whiskers”分裂，信息增益为 0.12。
• 由于“Ear shape”的信息增益最高，因此算法选择它作为第一个分裂特征。

3.5 决策树学习算法流程

决策树的学习是一个递归分裂（Recursive splitting的算法，其流程如下：

1. 从根节点开始，该节点包含所有训练样本。
2. 计算所有可用特征的信息增益，选择信息增益最高的特征。
3. 根据所选特征将数据集分裂，创建新的分支和子节点。
4. 对每个子节点，递归地重复步骤2和3，直到满足预设的停止条件。

如图所示，在根据“Ear shape”分裂后，算法会对“Pointy”和“Floppy”两个子节点分别应用相同的逻辑，继续寻找最佳分裂特征（“Face shape”和“Whiskers”），从而构建出完整的决策树。