用Python来学微积分23-微分中值定理

数学与Python的完美结合，让抽象定理活起来

微分中值定理是微积分学的核心内容，它如同一条纽带连接着函数与导数，帮助我们从局部性质推断整体行为。今天，我将用生动有趣的方式带你深入理解这三个重要定理，并结合Python代码让它们“活”起来。

一、罗尔定理：寻找平稳时刻

罗尔定理是微分中值定理家族的基础。它告诉我们：如果一段旅程的起点和终点高度相同，那么途中至少有一个时刻你的瞬时速度为零。

定理内容

如果函数f(x)满足以下条件：

• 在闭区间[a,b]上连续
• 在开区间(a,b)内可导
• f(a) = f(b)

则在(a,b)内至少存在一点ξ，使得f’(ξ) = 0。

手动证明过程

证明过程基于一个直观的想法：如果函数不是常数，那么它必须在某个点达到最大值或最小值。

由于f(x)在[a,b]上连续，根据闭区间上连续函数的性质，它在该区间上必定取得最大值M和最小值m。

现在考虑两种情况：

1. 如果M = m，则函数在[a,b]上恒为常数，导函数处处为零，定理自然成立。
2. 如果M > m，由于f(a) = f(b)，最大值和最小值不可能同时在端点取得，至少有一个在区间内部某点ξ处取得。又因为函数在(a,b)内可导，根据费马引理，该点处导数f’(ξ) = 0。

Python可视化验证

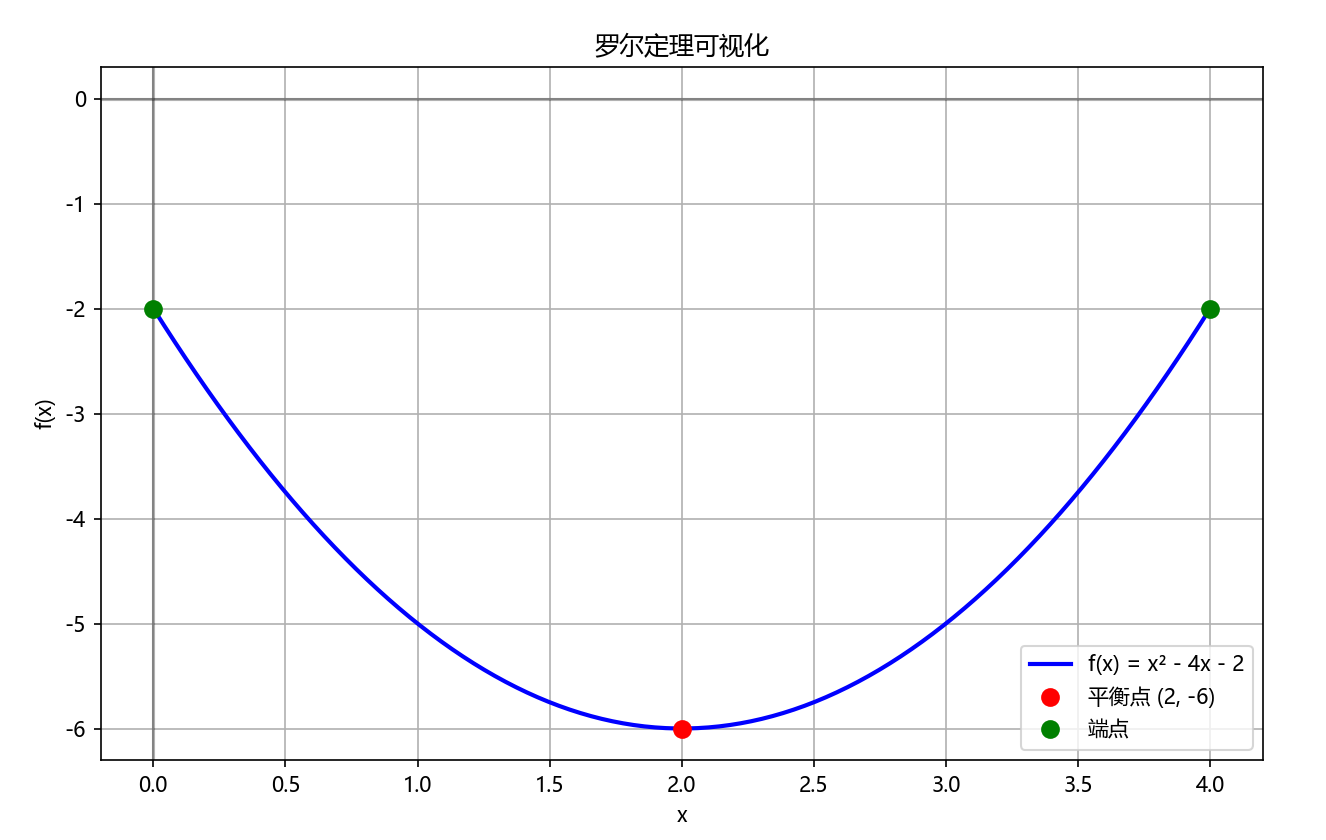
手动求解示例： 考虑函数f(x) = x² - 4x - 2在区间[0,4]上：

1. 检查条件：f(0) = -2, f(4) = -2，满足f(0)=f(4)
2. 求导：f’(x) = 2x - 4
3. 令f’(x) = 0：2x - 4 = 0 → x = 2

所以，在x=2处，切线是水平的！

import numpy as np
import matplotlib.pyplot as plt# 设置中文字体
plt.rcParams['font.sans-serif'] = ['Microsoft YaHei']
plt.rcParams['axes.unicode_minus'] = False# 定义函数
def f(x):return x**2 - 4*x - 2# 定义导函数
def df(x):return 2*x - 4# 在区间[0,4]上绘制函数图像
x = np.linspace(0, 4, 100)
y = f(x)# 找到导数为0的点
a, b = 0, 4
xi = 2  # 我们手动计算的结果plt.figure(figsize=(10, 6))
plt.plot(x, y, 'b-', linewidth=2, label='f(x) = x² - 4x - 2')
plt.axhline(y=0, color='k', linestyle='-', alpha=0.3)
plt.axvline(x=0, color='k', linestyle='-', alpha=0.3)
plt.plot([xi], [f(xi)], 'ro', markersize=8, label='平衡点 (2, -6)')
plt.plot([a, b], [f(a), f(b)], 'go', markersize=8, label='端点')
plt.title("罗尔定理可视化")
plt.xlabel("x")
plt.ylabel("f(x)")
plt.legend()
plt.grid(True)
plt.show()print(f"f(0) = {f(0)}, f(4) = {f(4)}")
print(f"在x={xi}处，导数值为：{df(xi)}")

应用实例：证明方程根的存在性

罗尔定理可用于证明方程根的存在性。例如，证明方程x³ - 3x² + 2x - 1 = 0在(0,2)内至少有一个实根。

设F(x) = x³ - 3x² + 2x - 1，我们需要找到a,b使得F(a)=F(b)。通过尝试，发现F(0) = -1，F(2) = -1，满足罗尔定理条件，因此存在ξ∈(0,2)使得F’(ξ)=0，即原方程有实根。

二、拉格朗日中值定理：罗尔定理的推广

拉格朗日定理去掉了罗尔定理中f(a)=f(b)的限制，是更一般情况下的中值定理。

定理内容

如果函数f(x)满足：

• 在闭区间[a,b]上连续
• 在开区间(a,b)内可导

则在(a,b)内至少存在一点ξ，使得： $$f^{\prime }(\xi )=\frac{f(b)-f(a)}{b-a}$$

手动证明过程

证明的关键是构造一个满足罗尔定理条件的辅助函数。

令： $$\phi (x)=f(x)-[f(a)+\frac{f(b)-f(a)}{b-a}(x-a)]$$

这个辅助函数表示曲线y=f(x)与弦AB的纵坐标之差。容易验证：

• φ(x)在[a,b]上连续
• φ(x)在(a,b)内可导
• φ(a) = φ(b) = 0

根据罗尔定理，存在ξ∈(a,b)使得φ’(ξ)=0，即： $$f^{\prime }(\xi )-\frac{f(b)-f(a)}{b-a}=0$$ $$f^{\prime }(\xi )=\frac{f(b)-f(a)}{b-a}$$

Python验证与可视化

手动求解示例： 考虑函数f(x) = x³在区间[-1,0]上：

1. 计算平均斜率：[f(0)-f(-1)]/[0-(-1)] = [0-(-1)]/1 = 1
2. 求导：f’(x) = 3x²
3. 令f’(x) = 平均斜率：3x² = 1 → x² = 1/3 → x = -√(1/3) ≈ -0.577

import numpy as np# 拉格朗日中值定理验证
def f(x):return x**3def df(x):return 3*x**2a, b = -1, 0
average_slope = (f(b) - f(a)) / (b - a)# 寻找满足条件的点
x_values = np.linspace(a, b, 1000)
for x in x_values:if abs(df(x) - average_slope) < 0.001:xi = xbreakprint(f"平均斜率: {average_slope}")
print(f"在x={xi:.3f}处，导数为: {df(xi):.3f}")
print(f"验证：两者是否接近？{abs(df(xi) - average_slope) < 0.001}")

运行结果:

有限增量公式

拉格朗日定理的一个重要推论是有限增量公式： $$f(x+\Delta x)-f(x)=f^{\prime }(\xi )\Delta x$$ 其中ξ在x与x+Δx之间。

这个公式给出了函数增量Δy的精确表达式，而不仅仅是近似值，在实际计算和理论证明中都有重要应用。

三、柯西中值定理：参数方程下的推广

柯西中值定理处理两个函数的情况，是拉格朗日定理的进一步推广。

定理内容

如果函数f(x)和g(x)满足：

• 在闭区间[a,b]上连续
• 在开区间(a,b)内可导
• g’(x) ≠ 0（对任意x∈(a,b)）

则在(a,b)内至少存在一点ξ，使得： $$\frac{f(b)-f(a)}{g(b)-g(a)}=\frac{f^{\prime }(\xi )}{g^{\prime }(\xi )}$$

手动证明过程

证明的关键是构造适当的辅助函数并应用罗尔定理。

首先，由g’(x) ≠ 0可知g(a) ≠ g(b)，否则与罗尔定理矛盾。

构造辅助函数： $$h(x)=f(x)-\frac{f(b)-f(a)}{g(b)-g(a)}g(x)$$

验证h(x)满足罗尔定理条件：

• h(x)在[a,b]上连续
• h(x)在(a,b)内可导
• h(a) = h(b)

因此存在ξ∈(a,b)使得h’(ξ)=0，即： $$f^{\prime }(\xi )-\frac{f(b)-f(a)}{g(b)-g(a)}{g}^{\prime }(\xi )=0$$ $$\frac{f(b)-f(a)}{g(b)-g(a)}=\frac{f^{\prime }(\xi )}{g^{\prime }(\xi )}$$

几何意义

柯西中值定理的几何意义是：用参数方程x=g(t), y=f(t)表示的曲线上，至少有一点切线平行于两端点的连线。

Python验证与应用

import numpy as np
import matplotlib.pyplot as plt# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False# 柯西中值定理的简单示例
def f(x):return x**2def g(x):return x**3def df(x):return 2*xdef dg(x):return 3*x**2a, b = 1, 2
left_side = (f(b) - f(a)) / (g(b) - g(a))# 寻找满足条件的点
found_point = None
for x in np.linspace(a, b, 1000):right_side = df(x) / dg(x)if abs(left_side - right_side) < 0.001:found_point = xprint(f"在x={x:.3f}处满足柯西中值定理")print(f"左边: {left_side:.3f}, 右边: {right_side:.3f}")break# ==================== 可视化部分 ====================# 创建图形和子图
fig, (ax1, ax2, ax3) = plt.subplots(1, 3, figsize=(18, 5))# 1. 函数图像：f(x) 和 g(x)
x_plot = np.linspace(0.5, 2.5, 100)
ax1.plot(x_plot, f(x_plot), 'b-', label='f(x) = x^2', linewidth=2)
ax1.plot(x_plot, g(x_plot), 'r-', label='g(x) = x^3', linewidth=2)
ax1.scatter([a, b], [f(a), f(b)], color='blue', s=50, zorder=5)
ax1.scatter([a, b], [g(a), g(b)], color='red', s=50, zorder=5)
ax1.axvline(a, color='gray', linestyle='--', alpha=0.7)
ax1.axvline(b, color='gray', linestyle='--', alpha=0.7)
ax1.set_xlabel('x')
ax1.set_ylabel('y')
ax1.set_title('函数 f(x) 和 g(x) 的图像')
ax1.legend()
ax1.grid(True, alpha=0.3)# 2. 参数曲线：(g(x), f(x))
x_param = np.linspace(a, b, 100)
ax2.plot(g(x_param), f(x_param), 'purple', linewidth=3, label='参数曲线 (g(x), f(x))')
ax2.scatter([g(a), g(b)], [f(a), f(b)], color='green', s=80, zorder=5, label='端点')if found_point is not None:# 绘制弦和切线# 弦：连接端点的直线chord_x = [g(a), g(b)]chord_y = [f(a), f(b)]ax2.plot(chord_x, chord_y, 'orange', linestyle='--', linewidth=2, label='弦')# 切线：在找到的点处tangent_slope = df(found_point) / dg(found_point)tangent_x = np.linspace(g(found_point)-0.5, g(found_point)+0.5, 10)tangent_y = f(found_point) + tangent_slope * (tangent_x - g(found_point))ax2.plot(tangent_x, tangent_y, 'red', linewidth=2, label='切线')# 标记中值点ax2.scatter([g(found_point)], [f(found_point)], color='red', s=100, zorder=5, label='中值点')ax2.set_xlabel('g(x)')
ax2.set_ylabel('f(x)')
ax2.set_title('参数空间中的柯西中值定理')
ax2.legend()
ax2.grid(True, alpha=0.3)# 3. 导函数比值的变化
x_deriv = np.linspace(a, b, 100)
right_sides = df(x_deriv) / dg(x_deriv)ax3.axhline(left_side, color='orange', linestyle='--', linewidth=2, label='左边值 (常数)')
ax3.plot(x_deriv, right_sides, 'green', linewidth=2, label='右边值 df(x)/dg(x)')if found_point is not None:ax3.axvline(found_point, color='red', linestyle=':', alpha=0.8, label=f'中值点 x={found_point:.3f}')ax3.scatter([found_point], [right_side], color='red', s=80, zorder=5)ax3.set_xlabel('x')
ax3.set_ylabel('导函数比值')
ax3.set_title('左右两边值的变化')
ax3.legend()
ax3.grid(True, alpha=0.3)plt.tight_layout()
plt.show()# ==================== 补充：验证定理的数值计算 ====================
print("\n" + "="*50)
print("柯西中值定理验证结果:")
print("="*50)
print(f"区间: [{a}, {b}]")
print(f"f(a) = {f(a):.3f}, f(b) = {f(b):.3f}")
print(f"g(a) = {g(a):.3f}, g(b) = {g(b):.3f}")
print(f"左边值 (f(b)-f(a))/(g(b)-g(a)) = {left_side:.3f}")if found_point is not None:print(f"找到的中值点: x = {found_point:.3f}")print(f"该点的右边值 df(x)/dg(x) = {right_side:.3f}")print(f"绝对误差: {abs(left_side - right_side):.6f}")
else:print("未找到满足条件的点，请调整阈值或检查函数")

运行结果:

四、微分中值定理的应用拓展

微分中值定理不仅有理论价值，还有丰富的实际应用：

1. 证明等式

例：证明当x∈(-1,1)时，arcsin x + arccos x = π/2

证：设f(x) = arcsin x + arccos x，则f’(x) = 1/√(1-x²) - 1/√(1-x²) = 0 由拉格朗日定理推论可知f(x)在(-1,1)上为常数。 又f(0) = arcsin 0 + arccos 0 = 0 + π/2 = π/2，故arcsin x + arccos x = π/2。

2. 证明不等式

例：证明当x>0时，e^x > 1 + x

证：设f(x) = e^x，在[0,x]上应用拉格朗日定理： 存在ξ∈(0,x)使得f’(ξ) = [f(x)-f(0)]/(x-0) 即e^ξ = (e^x - 1)/x 由于ξ>0时e^{ξ>1，所以(e}x-1)/x > 1，即e^x > 1 + x。

3. 求极限

微分中值定理与洛必达法则结合，可以解决更复杂的极限问题。

五、互动与实践

亲爱的读者，微分中值定理的美妙之处在于它将局部性质与整体行为联系起来。尝试以下练习巩固理解：

1. 手动计算：对函数f(x) = x³ - 3x在区间[-1,1]上验证罗尔定理，并找出所有满足条件的ξ值。
2. Python探索：修改上面代码中的函数定义和区间，观察定理成立的条件。
3. 实际问题：你能用这些定理解决生活中的什么实际问题？

如果这篇文章对你有帮助，请点赞和关注，我会带来更多精彩的数学内容！在评论区分享你的学习心得或疑问吧！

---

往期精彩回顾：

• 用Python来学微积分22-费马定理
• 用Python来学微积分21-玩转高阶导数

专栏导航目录 《程序员AI之路：从Python起步》完全学习导航

完整代码已开源 ai-learning-path，欢迎Star和Fork！

下期预告：在下一篇文章中，我们将开始学习洛必达法则。

---

参考资料：

1. 扈志明《微积分》教材

互动邀请：如果你对本章内容有独特的理解或在实际应用中遇到过有趣的问题，欢迎在评论区分享交流！