数据结构（10）

目录

图的存储结构——链式存储结构

2、十字链表（适用于有向图）

（1）十字链表的结构组成

（2）结构示意（以有向图为例）

（3）十字链表的核心优势

（4）适用场景

（5）与邻接表的对比

（6）例题

3、邻接多重表（适用于无向图 —> 对边操作）

（1）邻接多重表的结构组成

（2）结构示意（以无向图为例）

（3）邻接多重表的核心优势

（4）与邻接表（无向图）的对比

（5）适用场景

图的存储结构——链式存储结构

2、十字链表（适用于有向图）

十字字链表（Orthogonal List）是有向图的一种高效链式存储结构，专为解决有向图中 “出边” 和 “入边” 的统一管理问题而设计。它通过顶点节点和弧节点的组合，同时记录每个顶点的出边（从该顶点出发的弧）和入边（指向该顶点的弧），避免了邻接表查询入边时的低效性。

（1）十字链表的结构组成

十字链表由两类节点构成：顶点节点和弧节点，具体结构如下：

①  顶点节点（Vertex Node）

每个顶点节点存储顶点的基本信息及两条关键指针，结构为：

┌─────────┬──────────────┬──────────────┐
│ data    │ first_out    │ first_in     │
│ 顶点值  │ 指向第一条出边 │ 指向第一条入边 │
└─────────┴──────────────┴──────────────┘

• data：顶点的具体值（如编号、名称）。
• first_out：指针，指向以该顶点为起点的第一条弧（出边的起始节点）。
• first_in：指针，指向以该顶点为终点的第一条弧（入边的起始节点）。

②  弧节点（Arc Node）

每条弧（有向边）对应一个弧节点，存储弧的起点、终点、权重（可选）及两条指针，结构为：

┌─────────┬─────────┬─────────┬──────────────┬──────────────┐
│ tailvex │ headvex │ weight  │ hlink        │ tlink        │
│ 弧尾(起点)│ 弧头(终点)│ 权重    │ 指向同终点的下一条弧 │ 指向同起点的下一条弧 │
└─────────┴─────────┴─────────┴──────────────┴──────────────┘

• tailvex：弧的起点（尾顶点）编号。
• headvex：弧的终点（头顶点）编号。
• weight：弧的权重（仅用于有向网，无权图可省略）。
• hlink：水平指针，指向与当前弧有相同终点的下一条弧（即同头弧，用于入边链表）。
• tlink：垂直指针，指向与当前弧有相同起点的下一条弧（即同尾弧，用于出边链表）。

（2）结构示意（以有向图为例）

假设有向图 G 包含顶点 {0,1,2}，弧为 <0,1>、<0,2>、<1,2>，其十字链表结构如下：

顶点节点数组（存储所有顶点）：

顶点0: data=0, first_out→弧<0,1>, first_in→null（无入边）
顶点1: data=1, first_out→弧<1,2>, first_in→弧<0,1>
顶点2: data=2, first_out→null（无出边）, first_in→弧<0,2>（或弧<1,2>，取决于链接顺序）

弧节点链表（出边与入边的交叉链接）：

• 弧 <0,1>：tailvex=0, headvex=1，tlink→弧<0,2>（同起点 0 的下一条出边），hlink→null（同终点 1 的下一条入边，暂无）。
• 弧 <0,2>：tailvex=0, headvex=2，tlink→null（0 的出边结束），hlink→弧<1,2>（同终点 2 的下一条入边）。
• 弧 <1,2>：tailvex=1, headvex=2，tlink→null（1 的出边结束），hlink→null（2 的入边结束）。

交叉链接逻辑：

• 出边方向（同尾弧）：顶点 0 的 first_out 指向 <0,1>，<0,1> 的 tlink 指向 <0,2>，形成 0 的出边链。
• 入边方向（同头弧）：顶点 2 的 first_in 指向 <0,2>，<0,2> 的 hlink 指向 <1,2>，形成 2 的入边链。

（3）十字链表的核心优势

1. 统一管理出边和入边：无需像邻接表那样额外维护 “逆邻接表”（入边表），通过顶点节点的 first_out 和 first_in 可直接访问出边链和入边链，兼顾了出度和入度的高效查询。

2. 遍历效率高：

   • 遍历顶点的所有出边：沿 first_out 顺 tlink 指针遍历（同邻接表的出边遍历，时间复杂度 O(k)，k 为出度）。
   • 遍历顶点的所有入边：沿 first_in 顺 hlink 指针遍历（无需扫描全图，时间复杂度 O(m)，m 为入度）。

3. 空间效率适中：存储 n 个顶点和 e 条弧的有向图，空间复杂度为 O(n+e)（顶点节点 O(n) + 弧节点 O(e)），与邻接表相当，适合稀疏有向图。

4. 便于弧的增删：增删一条弧时，只需修改对应顶点的 first_out/first_in 指针及弧节点的 tlink/hlink 指针，操作灵活（时间复杂度 O(1) 用于表头插入）。

（4）适用场景

• 需频繁同时查询出边和入边的有向图操作（如计算顶点的出度和入度、判断顶点间的双向弧、拓扑排序等）。
• 稀疏有向图或有向网（避免邻接矩阵的空间浪费，同时解决邻接表入边查询低效的问题）。
• 图算法中需同时处理起点和终点关联弧的场景（如最大流算法、有向图的连通性分析）。

（5）与邻接表的对比

特性	邻接表（有向图）	十字链表（有向图）
入边查询	需遍历全图（O(n+e)）或维护逆邻接表（额外空间）	直接沿 first_in 和 hlink 遍历（O(m)，m 为入度）
空间开销	O(n+e)（仅存储出边）	O(n+e)（同时存储出边和入边的链接关系）
结构复杂度	简单（单链表）	较复杂（交叉链表）
适用操作	以出边为主的操作（如 DFS）	需同时处理出边和入边的操作（如拓扑排序、入度计算）

（6）例题

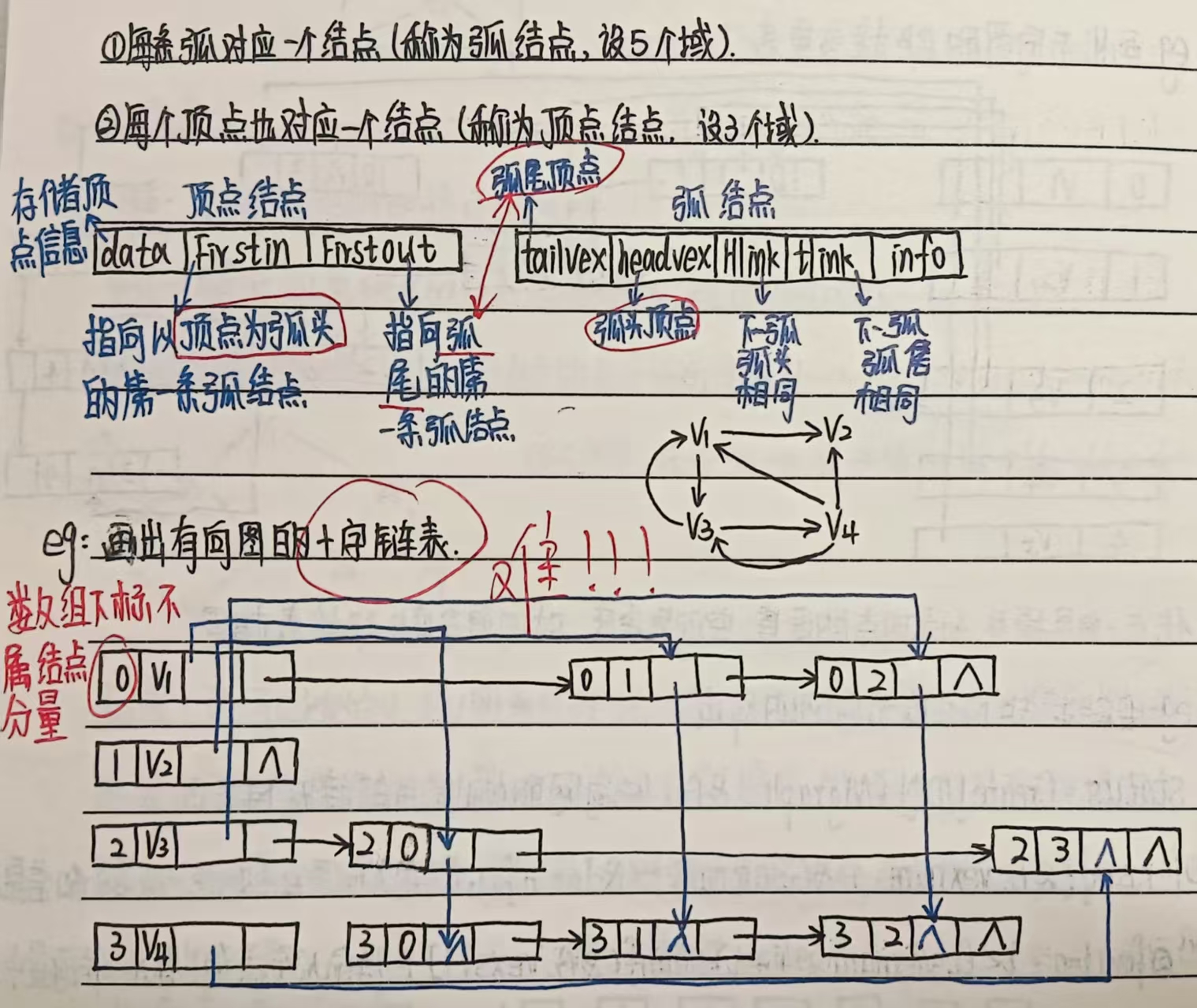
3、邻接多重表（适用于无向图 —> 对边操作）

邻接多重表（Adjacency Multilist）是无向图的一种高效链式存储结构，专为解决无向图中 “边的双向性” 和 “边的操作效率” 问题而设计。它通过将无向图中每条边用一个节点表示（而非邻接表中的两个节点），并通过指针关联边的两个顶点，实现对边的直接访问和修改，尤其适合频繁对边执行增删、标记等操作的场景（如遍历中标记已访问的边）。

（1）邻接多重表的结构组成

邻接多重表由两类节点构成：顶点节点和边节点，具体结构如下：

①  顶点节点（Vertex Node）

每个顶点节点存储顶点的基本信息及一条指针，结构为：

┌─────────┬──────────────┐
│ data    │ first_edge   │
│ 顶点值  │ 指向第一条关联边 │
└─────────┴──────────────┘

• data：顶点的具体值（如编号、名称）。
• first_edge：指针，指向与该顶点相关联的第一条边节点（即以该顶点为端点的任意一条边）。

②  边节点（Edge Node）

无向图中每条边对应唯一的边节点，存储边的两个端点、权重（可选）及两条指针，结构为：

┌─────────┬─────────┬─────────┬──────────────┬──────────────┐
│ mark    │ ivex    │ jvex    │ ilink        │ jlink        │
│ 标记位  │ 端点i   │ 端点j   │ 指向i的下一条边 │ 指向j的下一条边 │
└─────────┴─────────┴─────────┴──────────────┴──────────────┘

• mark：标记位（如用于遍历中标记边是否已被访问，取值 0 或 1）。
• ivex 和 jvex：边的两个端点（顶点编号，无向图中无顺序）。
• ilink：指针，指向与 ivex 相关联的下一条边节点（即与顶点 ivex 相连的其他边）。
• jlink：指针，指向与 jvex 相关联的下一条边节点（即与顶点 jvex 相连的其他边）。

（2）结构示意（以无向图为例）

假设有无向图 G 包含顶点 {0,1,2,3}，边为 (0,1)、(0,2)、(1,2)、(1,3)，其邻接多重表结构如下：

顶点节点数组（存储所有顶点）：

顶点0: data=0, first_edge→边(0,1)
顶点1: data=1, first_edge→边(0,1)
顶点2: data=2, first_edge→边(0,2)
顶点3: data=3, first_edge→边(1,3)

边节点链表（边与顶点的关联逻辑）：

• 边 (0,1)：ivex=0, jvex=1，ilink→边(0,2)（顶点 0 的下一条边），jlink→边(1,2)（顶点 1 的下一条边），mark=0。
• 边 (0,2)：ivex=0, jvex=2，ilink→null（顶点 0 的边结束），jlink→边(1,2)（顶点 2 的下一条边），mark=0。
• 边 (1,2)：ivex=1, jvex=2，ilink→边(1,3)（顶点 1 的下一条边），jlink→null（顶点 2 的边结束），mark=0。
• 边 (1,3)：ivex=1, jvex=3，ilink→null（顶点 1 的边结束），jlink→null（顶点 3 的边结束），mark=0。

关联逻辑：

• 顶点 0 的边链：通过 first_edge 指向边 (0,1)，再沿边 (0,1) 的 ilink 指向边 (0,2)（0 的所有边）。
• 顶点 1 的边链：通过 first_edge 指向边 (0,1)，再沿边 (0,1) 的 jlink 指向边 (1,2)，再沿边 (1,2) 的 ilink 指向边 (1,3)（1 的所有边）。

（3）邻接多重表的核心优势

1. 边的唯一性：无向图中每条边仅用一个边节点表示（而非邻接表中两个边节点），避免了邻接表中 “一条边被存储两次” 的冗余，且便于直接操作边（如标记、删除）。例如，遍历中标记边是否访问时，只需修改一个边节点的 mark 位，无需同步修改两个节点。

2. 高效的边操作：

   • 增删边时，只需修改相关顶点的 first_edge 指针及边节点的 ilink/jlink 指针，操作一次即可（邻接表需修改两个边节点）。
   • 查询边是否存在时，可从任意一个端点出发遍历边链，找到目标边节点即可（无需像邻接表那样检查两个方向）。

3. 兼顾空间与效率：存储 n 个顶点和 e 条边的无向图，空间复杂度为 O(n+e)（顶点节点 O(n) + 边节点 O(e)），与邻接表（O(n+2e)）相比更节省空间，尤其适合边数多的图。

4. 便于遍历与标记：在图的遍历（如深度优先搜索）中，需标记已访问的边以避免重复处理（无向图中一条边对应两个方向的遍历），邻接多重表的 mark 位可直接实现这一功能，无需额外存储空间。

（4）与邻接表（无向图）的对比

特性	邻接表（无向图）	邻接多重表（无向图）
边的存储方式	每条边用两个边节点表示（分别属于两个端点的链表）	每条边用一个边节点表示（同时关联两个端点）
空间复杂度	O(n+2e)（边节点冗余）	O(n+e)（无冗余）
边的标记 / 删除操作	需同步修改两个边节点，操作繁琐且易出错	只需修改一个边节点，操作简单高效
边的查询效率	需检查两个端点的链表，可能重复遍历	从任意端点遍历一次即可，无重复
结构复杂度	简单（单链表）	较复杂（边节点需关联两个顶点的边链）

（5）适用场景

• 需频繁对边执行操作的无向图应用（如标记已访问的边、删除特定边、统计边的数量等）。
• 无向图的遍历算法（如求欧拉回路、判断边是否被访问），避免重复处理边。
• 稀疏或稠密无向图均可，但对边操作频繁的场景优势更明显（如地图中的道路删除、网络中的链路断开）。