[优选算法专题四.前缀和——NO.30 和可被 K 整除的子数组]

题目链接：

和可被 K 整除的子数组

题目描述：

题目解析：

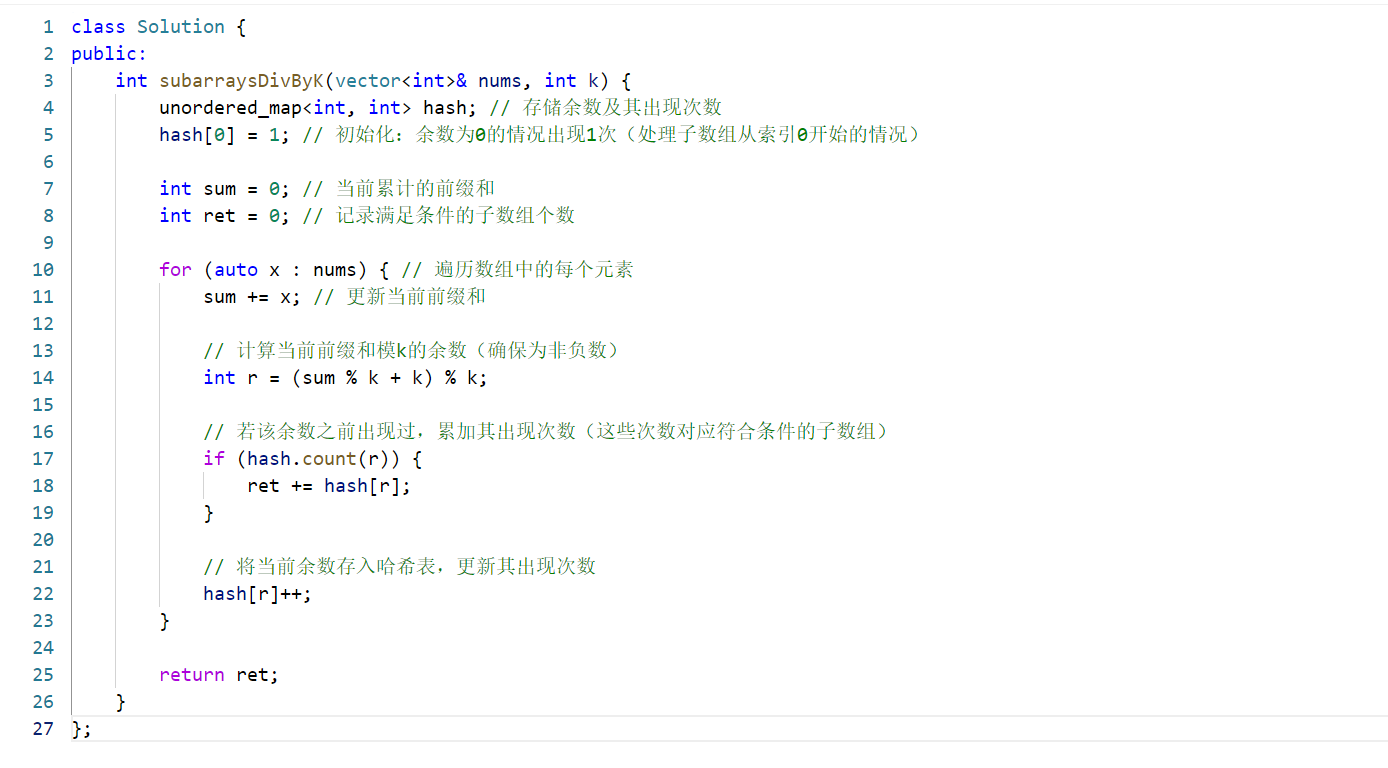
核心思路

基于前缀和与同余定理，结合哈希表优化，将时间复杂度从暴力解法的 O (n²) 降至 O (n)。

1️⃣前缀和与子数组和的关系：设 sum[i] 为前 i 个元素的前缀和（nums[0] + ... + nums[i-1]），则子数组 nums[j..i-1] 的和为 sum[i] - sum[j]。

2️⃣同余定理的应用：若子数组和 sum[i] - sum[j] 能被 k 整除，则 (sum[i] - sum[j]) % k == 0。根据同余定理，这等价于 sum[i] % k == sum[j] % k（即两个前缀和模 k 的余数相同）。因此，问题转化为：统计 “当前前缀和的余数” 在之前出现过的次数，累加这些次数即可得到符合条件的子数组个数。

3️⃣哈希表的作用：用哈希表 hash 存储前缀和模 k 的余数与该余数出现的次数，实时记录遍历过程中余数的出现频率，避免重复计算。

关键细节

• 余数非负化处理：由于 sum 可能为负数（数组含负数时），直接取模可能得到负余数（例如 sum = -1, k = 5 时，-1 % 5 = -1）。通过 (sum % k + k) % k 可将负余数转为正余数（上例中结果为 4），确保同余判断的正确性。

• 初始化 hash[0] = 1：当 sum % k == 0 时（即子数组从索引 0 开始到当前位置的和可被 k 整除），需要统计这种情况，因此初始时余数 0 的出现次数为 1。

• 遍历顺序：先计算当前余数并检查哈希表，再更新哈希表，避免将当前余数误算入统计（确保子数组是 “之前的前缀和” 与 “当前前缀和” 的差）。

复杂度分析

• 时间复杂度：O (n)，其中 n 是数组长度。遍历数组一次，哈希表的插入和查询操作均为 O (1)（平均情况）。
• 空间复杂度：O (min (n, k))，哈希表中最多存储 k 个不同的余数（因为模 k 的余数范围是 0 到 k-1），极端情况下可能存储 n 个（当 k > n 且所有余数不同时）。