【机器学习03】学习率与特征工程、多项式回归、逻辑回归

---

视频链接
吴恩达机器学习p21-p31

注明：受markdown语法所限， x⃗表示x向量

---

一、线性回归的实践技巧

在前一篇文章中，我们已经学习了线性回归的模型、代价函数以及梯度下降算法。在这一部分，我们将探讨一些让模型训练更高效、功能更强大的实用技巧。

1.1 调试梯度下降

梯度下降是一个迭代过程，我们如何确保它在正确地工作呢？关键在于监控代价函数 J 的变化。

1.1.1 学习曲线 (Learning Curve)

一个行之有效的方法是绘制学习曲线（Learning Curve），即以梯度下降的迭代次数（# iterations为横轴，代价函数 J(w⃗, b) 的值为纵轴。

• 正常表现：一条正常的学习曲线应该是单调递减的。随着迭代次数的增加，代价 J 的值会不断下降，最终趋于平缓，表明算法已经收敛（converged）。
• 自动收敛测试：在代码中，我们可以设置一个自动收敛的判断标准。例如，设定一个很小的阈值 ε (epsilon，如 0.001)，如果在一次迭代中，J 值的下降小于这个阈值，我们就可以认为算法已经收敛。

1.1.2 如何选择学习率 α

学习率 α 的选择对梯度下降的性能至关重要。学习曲线可以帮助我们诊断 α 是否合适。

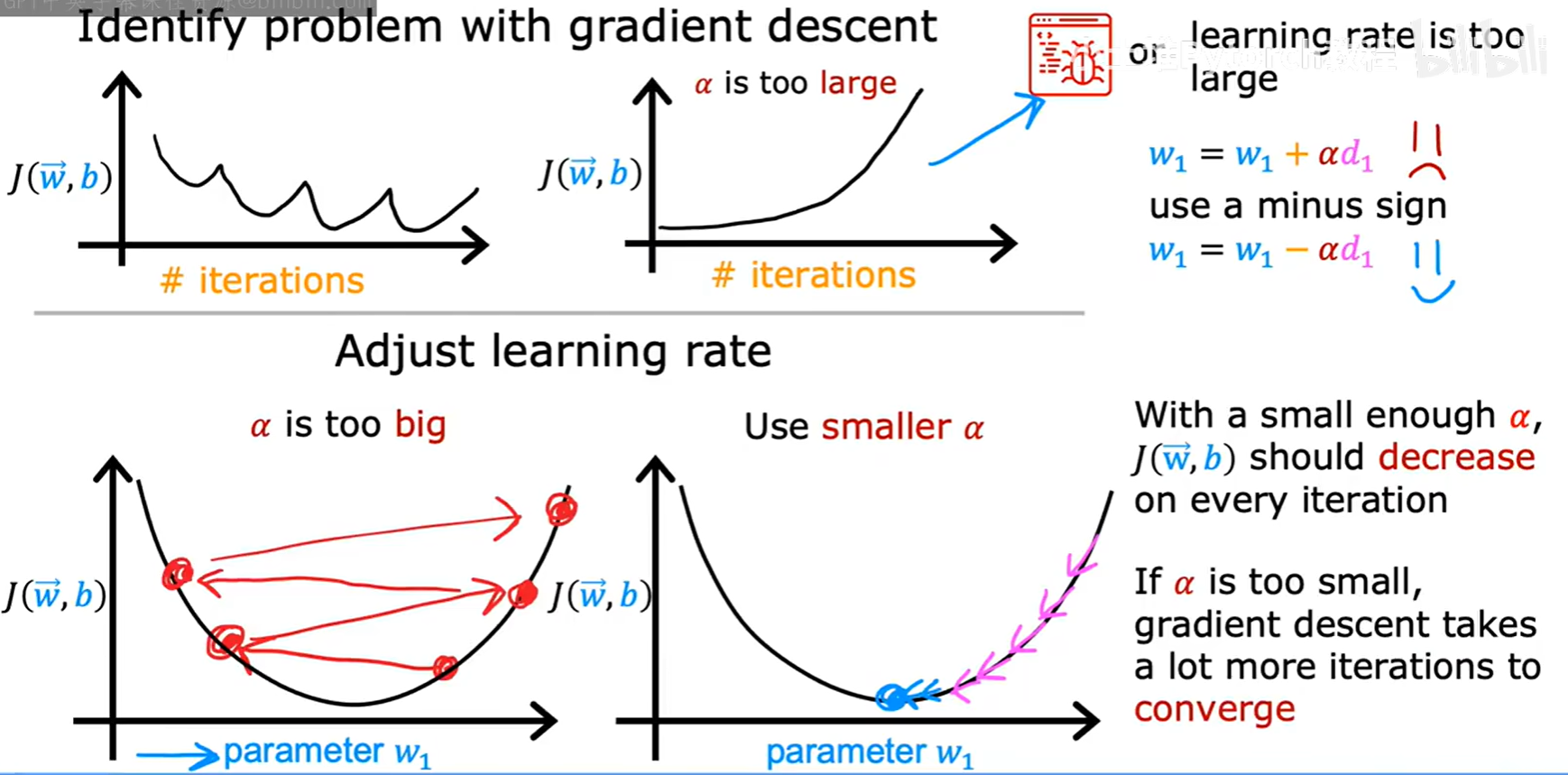
• α 过大：如果学习曲线不降反升，或者上下剧烈震荡，这通常意味着学习率 α 设置得太大了，导致算法在最低点附近“反复横跳”，甚至发散。解决方法是使用更小的 α。
• α 过小：如果代价 J 下降得非常缓慢，说明学习率 α 可能太小了，需要很长时间才能收敛。

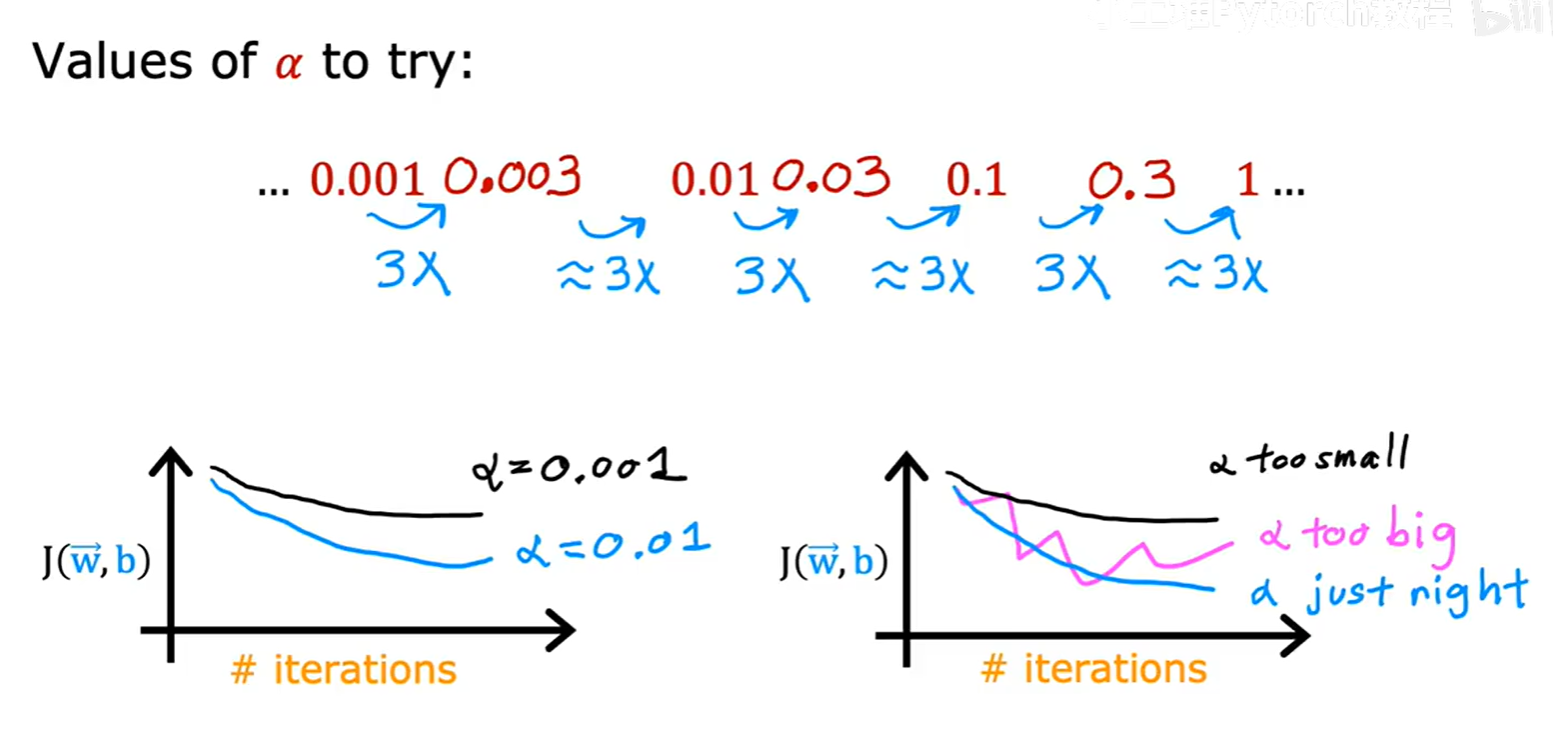
在实践中，选择 α 的一个好方法是尝试一系列呈倍数增长的数值，例如：..., 0.001, 0.003, 0.01, 0.03, 0.1, 0.3, 1, ...（每次大约乘以3）。通过比较不同 α 值下的学习曲线，我们可以快速找到一个既能确保收敛又不会太慢的合适值。

1.2 特征工程 (Feature Engineering)

除了调整算法本身，我们还可以通过特征工程来提升模型的性能。特征工程指的是利用我们对问题的理解和直觉，通过对原始特征进行变换或组合，来创造出新的、可能更有用的特征。

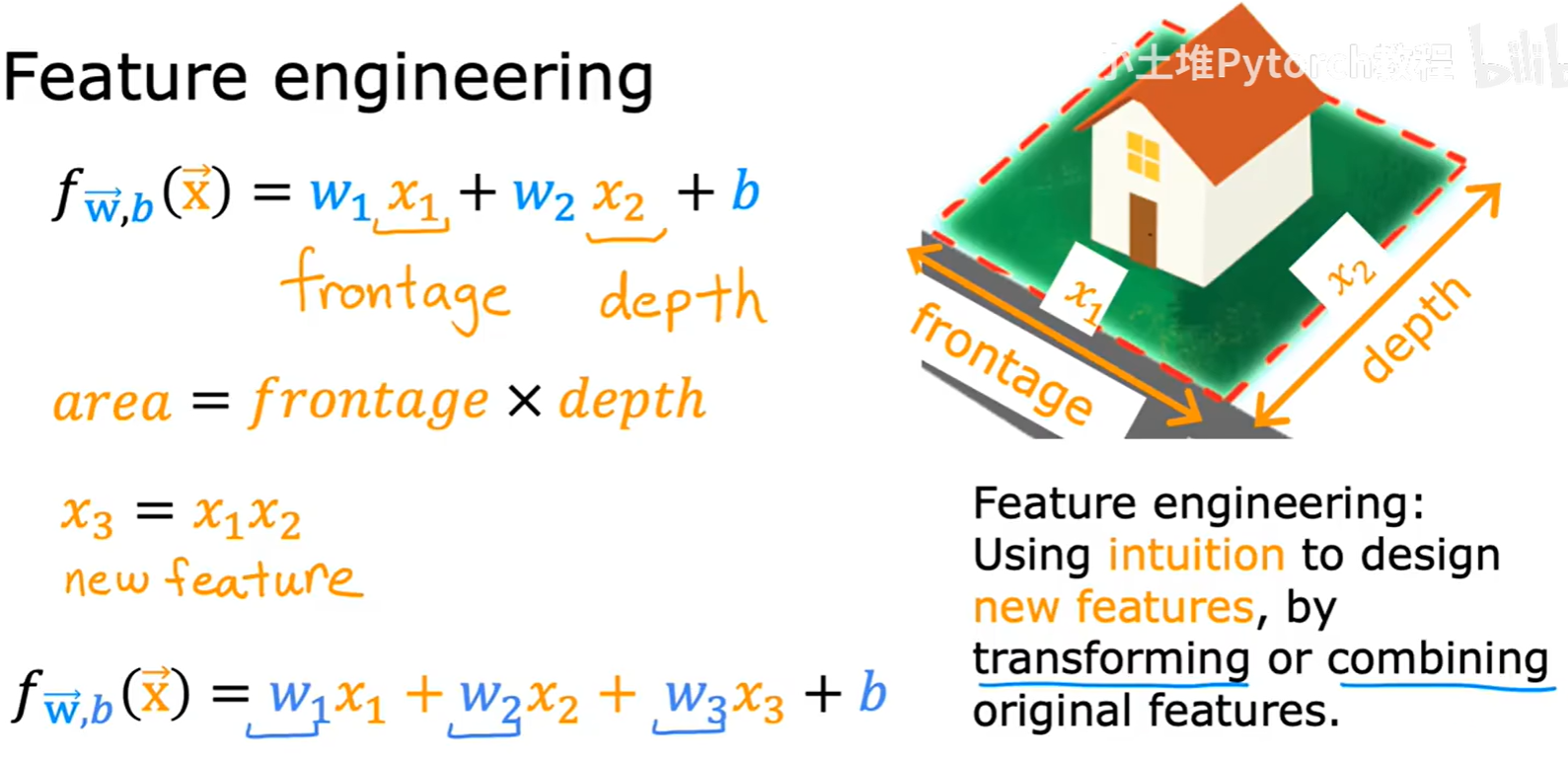
例如，在房价预测中，我们有两个原始特征：房屋的临街宽度 x₁ (frontage) 和纵深 x₂ (depth)。我们知道，房屋的面积（area是决定价格的关键因素。因此，我们可以创造一个新特征 x₃ = x₁ * x₂，并将其加入到模型中。这样，模型就可能更好地捕捉到房价与面积之间的关系。

1.3 多项式回归 (Polynomial Regression)

有时候，数据点之间的关系并不是一条直线。为了拟合这些非线性的数据，我们可以使用多项式回归（Polynomial Regression）。

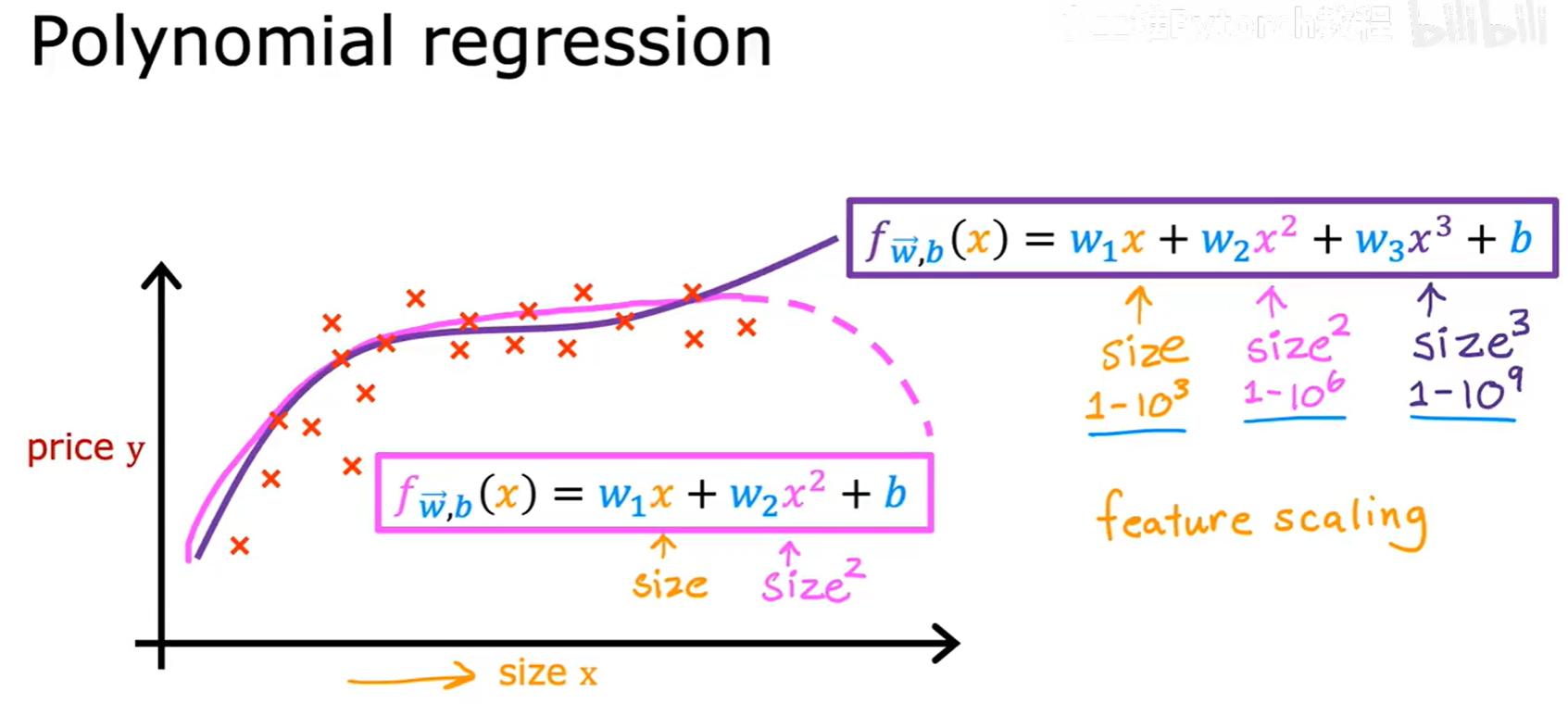
实现多项式回归的核心思想，就是通过特征工程，将原始特征的多次方作为新的特征。例如，我们可以将原来的模型：
f(x) = w₁x + b
扩展为二次或三次模型：
f(x) = w₁x + w₂x² + b
f(x) = w₁x + w₂x² + w₃x³ + b

通过添加这些高次项特征，我们的模型就能拟合出各种弯曲的曲线，从而更好地适应非线性的数据模式。

注意：在使用多项式回归时，特征的尺度会变得差异巨大（例如 x 在 1-1000，x³ 就在 1-10⁹），此时特征缩放变得至关重要。

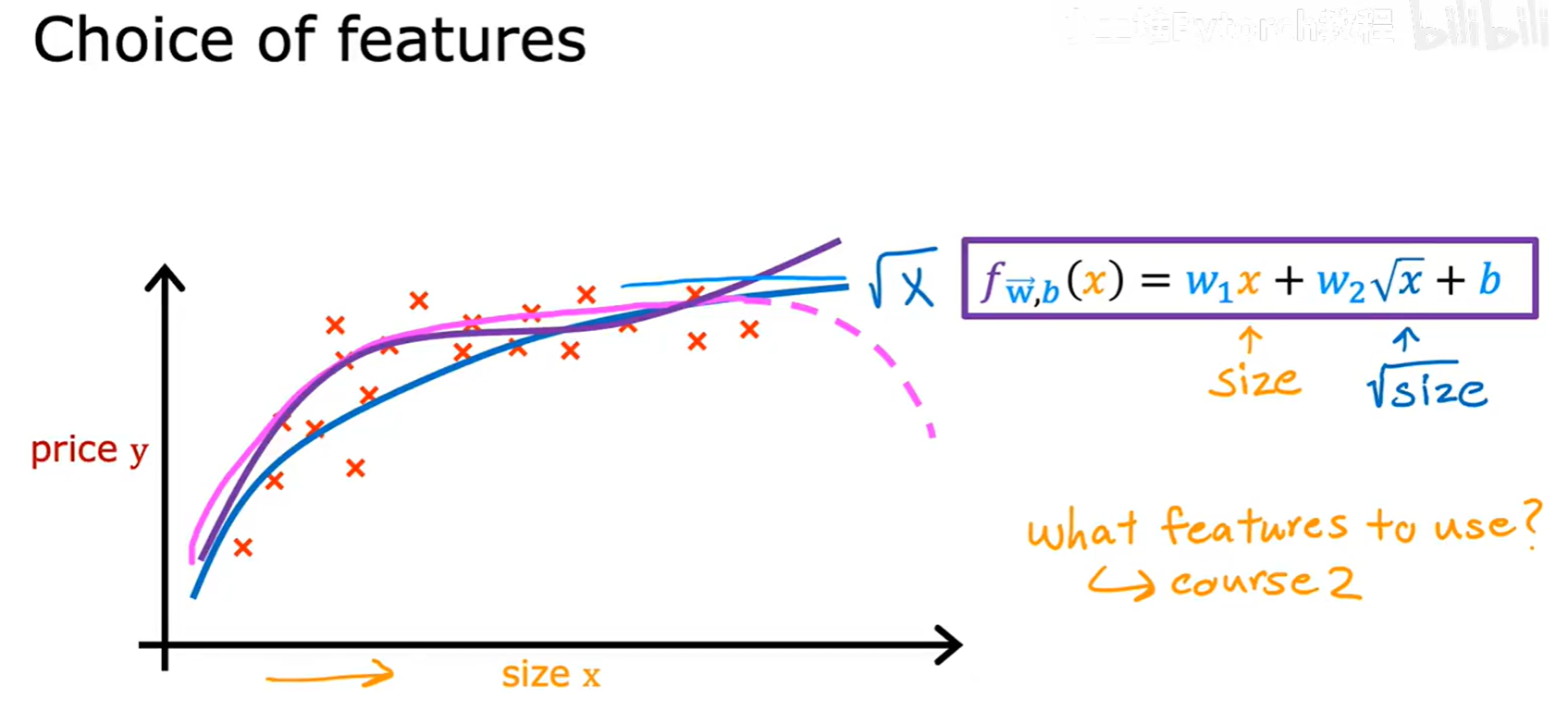
我们甚至可以尝试各种函数变换，比如 √x 等。如何选择最合适的特征，是机器学习中一个更深入的课题。

二、逻辑回归与分类问题

到目前为止，我们都在讨论回归（Regression问题，即预测一个连续的数值。现在，我们将转向机器学习的另一个核心领域：分类（Classification）。

2.1 什么是分类问题

分类问题的目标是预测一个离散的类别。

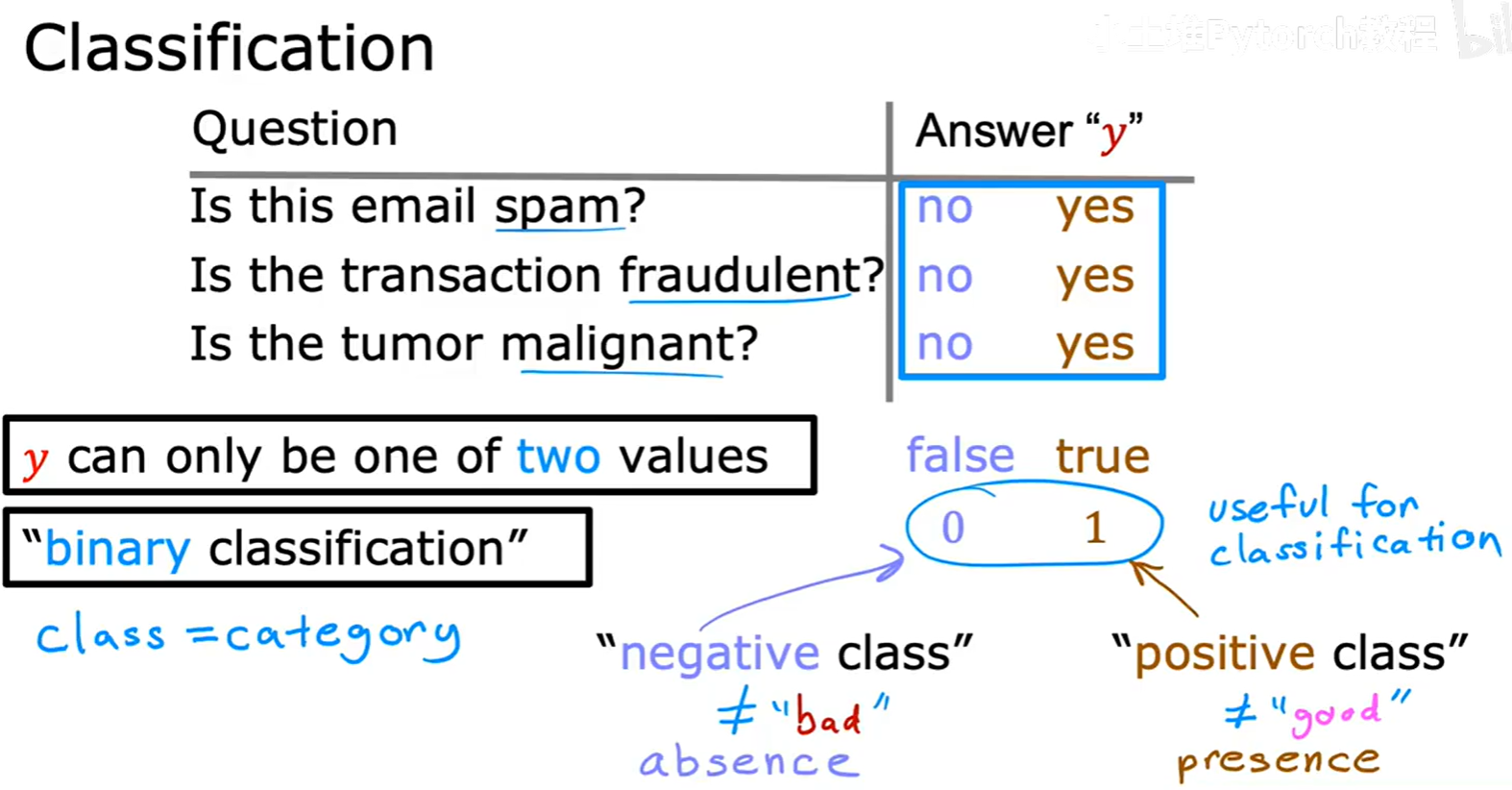
例如：

• 这封邮件是垃圾邮件吗？（是/否）
• 这笔交易是欺诈性的吗？（是/否）
• 这个肿瘤是恶性的吗？（是/否）

当类别只有两种时，我们称之为二元分类（Binary Classification）。习惯上，我们用 0 和 1 来代表这两个类别。例如，0 代表“良性肿瘤”（负类），1 代表“恶性肿瘤”（正类）。

2.1.1 线性回归用于分类的局限

我们可能会想，能否直接用线性回归来解决分类问题呢？答案是否定的。

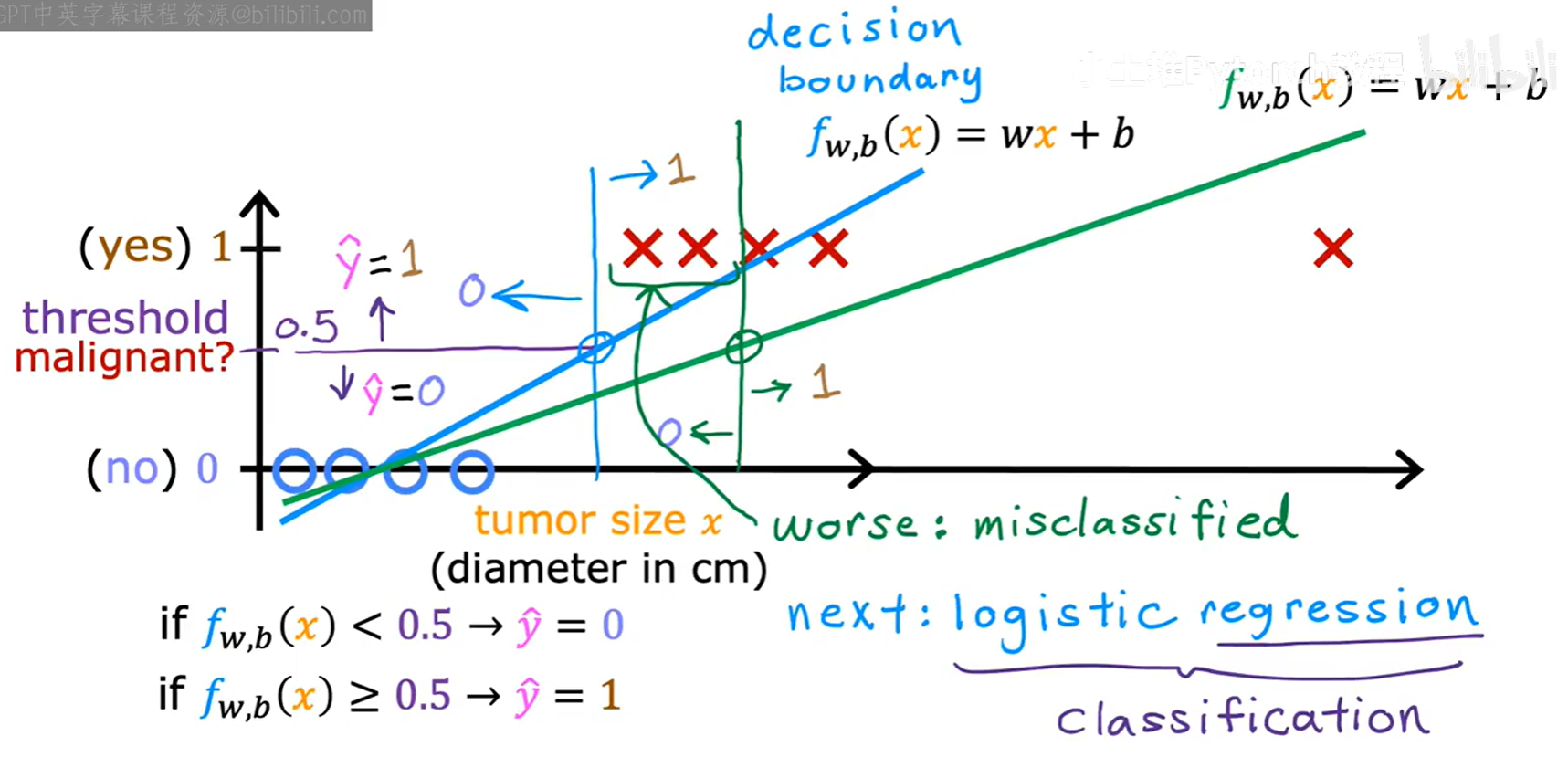
如果直接用线性回归拟合分类数据，模型的输出值可能会远大于1或远小于0，这在分类场景下没有实际意义。并且，线性模型往往无法很好地拟合分类数据的决策边界。因此，我们需要一个专门为分类问题设计的算法——逻辑回归（Logistic Regression）。

2.2 逻辑回归模型

逻辑回归的核心思想是，将线性回归的输出结果，通过一个特殊的函数，“压缩”到 0 和 1 之间。

2.2.1 Sigmoid 函数

这个起关键作用的函数被称为 Sigmoid 函数，也叫 Logistic 函数。

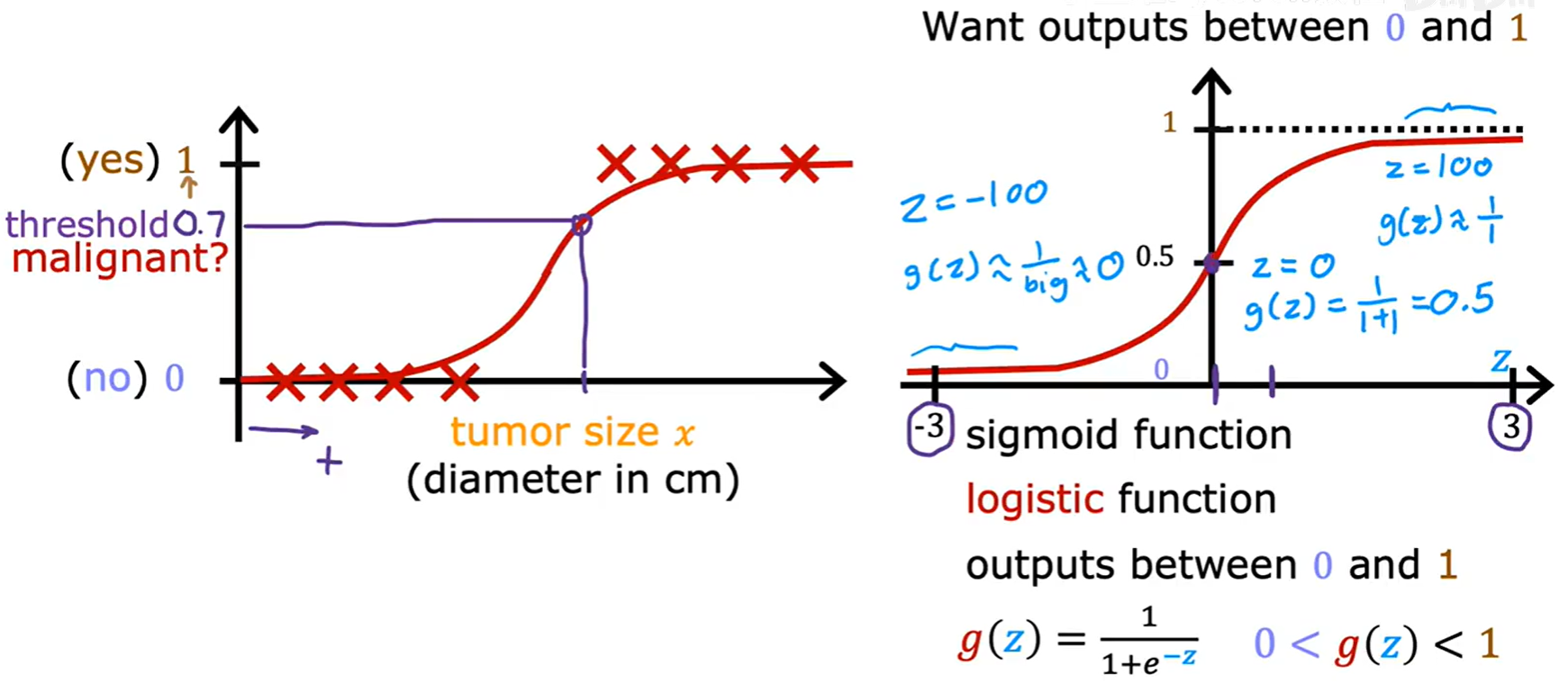
其数学表达式为：g(z) = 1 / (1 + e⁻ᶻ)

它的特性是：无论输入 z 的值有多大或多小，输出 g(z) 的值永远在 0 和 1 之间。

2.2.2 模型表示与解读

逻辑回归模型将线性部分 z = w⃗ · x⃗ + b 的输出，作为 Sigmoid 函数的输入。

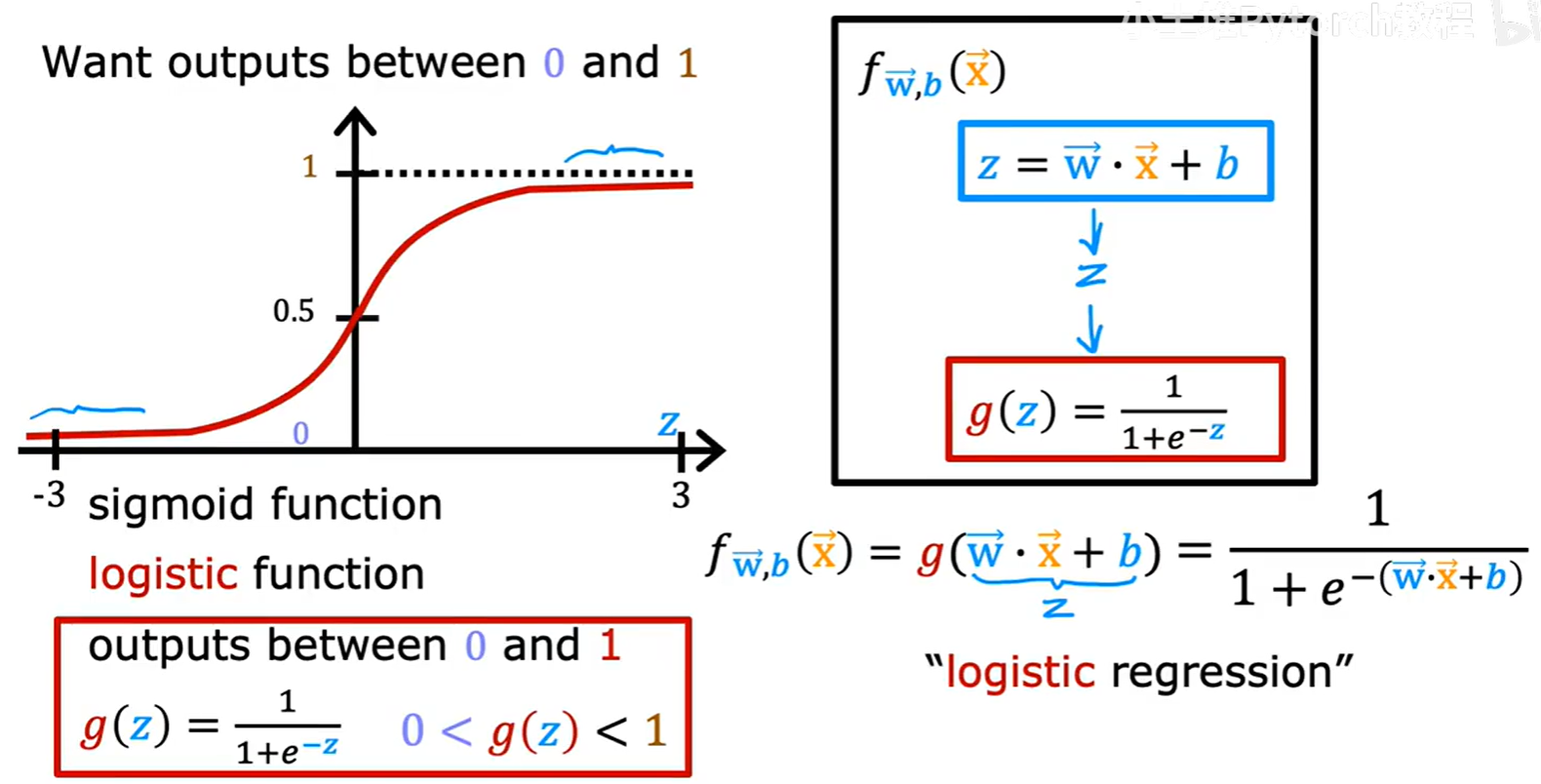
完整的模型表达式为：
f_w⃗,b(x⃗) = g(w⃗ · x⃗ + b) = 1 / (1 + e⁻⁽ʷ⃗·ˣ⃗⁺ᵇ⁾)

逻辑回归模型的输出值 f(x) 有一个非常好的概率解释：它代表了在给定输入 x 的条件下，预测类别为 1 的概率。即：
f(x) = P(y=1 | x; w⃗, b)

例如，如果模型对一个肿瘤样本输出 0.7，这意味着模型认为该肿瘤有70%的概率是恶性（y=1）的。

2.3 决策边界 (Decision Boundary)

有了概率输出后，我们如何做出最终的分类决策呢？通常我们以 0.5 作为阈值。

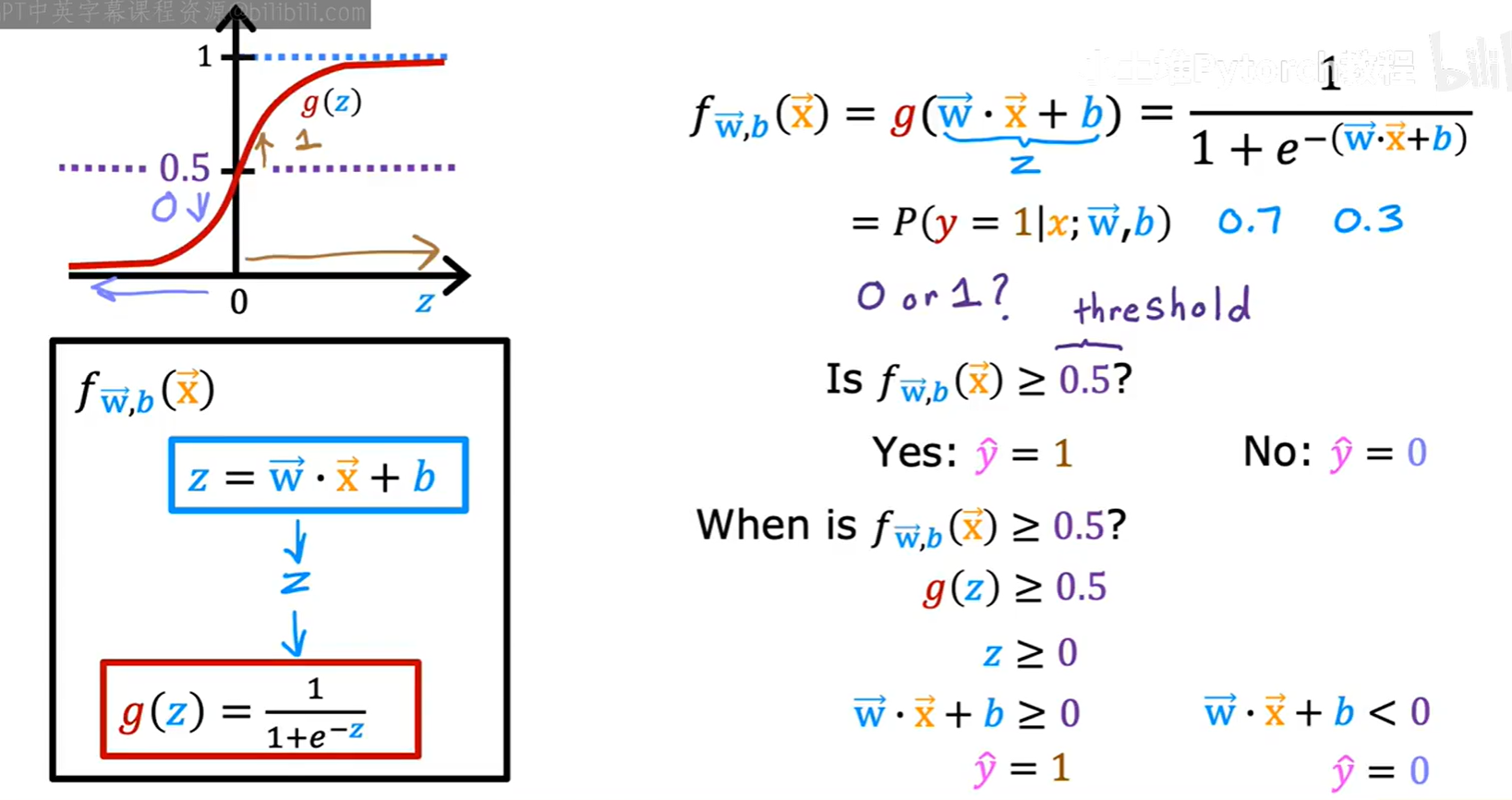
• 如果 f(x) ≥ 0.5，则预测 ŷ = 1。
• 如果 f(x) < 0.5，则预测 ŷ = 0。

由于 Sigmoid 函数 g(z) 在 z=0 时取值为 0.5，所以上述决策规则等价于：

• 如果 z = w⃗ · x⃗ + b ≥ 0，则预测 ŷ = 1。
• 如果 z = w⃗ · x⃗ + b < 0，则预测 ŷ = 0。

此时，由方程 z = w⃗ · x⃗ + b = 0 所定义的线（或面、超平面）就成为了决策边界（Decision Boundary）。它将特征空间一分为二，一边是预测为 1 的区域，另一边是预测为 0 的区域。

2.3.1 线性决策边界

当 z 是特征的线性组合时，决策边界就是线性的。

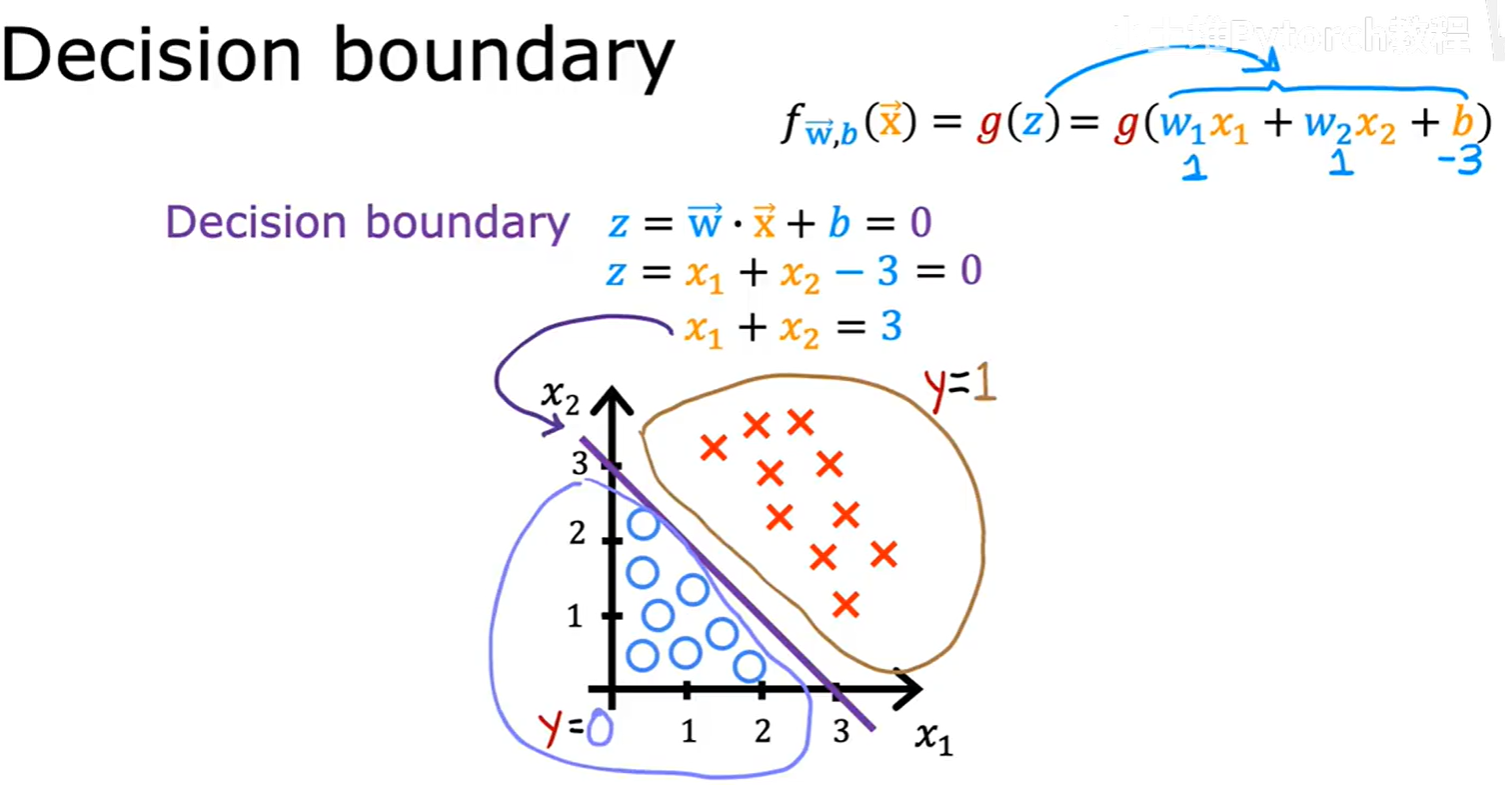
例如，如果 z = x₁ + x₂ - 3 = 0，那么决策边界就是一条直线 x₁ + x₂ = 3。

2.3.2 非线性决策边界

逻辑回归的强大之处在于，通过结合特征工程（例如多项式特征），它可以学习到非常复杂的非线性决策边界。

例如，如果我们创建一个模型 g(w₁x₁² + w₂x₂² + b)，并假设学习到的参数使得 z = x₁² + x₂² - 1 = 0，那么决策边界就是一个圆形 x₁² + x₂² = 1。

通过引入更复杂的多项式特征，逻辑回归可以拟合出椭圆、甚至任意形状的决策边界，使其能够解决高度复杂的分类问题。

三、逻辑回归的代价函数

我们已经定义了逻辑回归的模型，接下来需要一个代价函数来衡量模型的预测与真实标签之间的差异，从而通过梯度下降来优化参数 w⃗ 和 b。

3.1 平方误差代价函数的局限性

我们可能会想，是否可以直接沿用线性回归中的平方误差代价函数？

J(w⃗, b) = (1/m) * Σ [ (f(x⁽ⁱ⁾) - y⁽ⁱ⁾)² ]

答案是否定的。因为逻辑回归的模型 f(x) 是一个非线性的 Sigmoid 函数，如果将它代入平方误差代价函数，会得到一个非凸（non-convex的函数。这种函数有很多局部最小值点，梯度下降算法很可能陷入其中一个，而无法保证找到全局最优解。

因此，我们需要为逻辑回归设计一个全新的、能够保证是凸函数的代价函数。

3.2 逻辑损失函数 (Logistic Loss Function)

为了构建总的代价函数（Cost Function），我们首先为单个训练样本定义一个损失函数（Loss Function） L(f(x), y)。

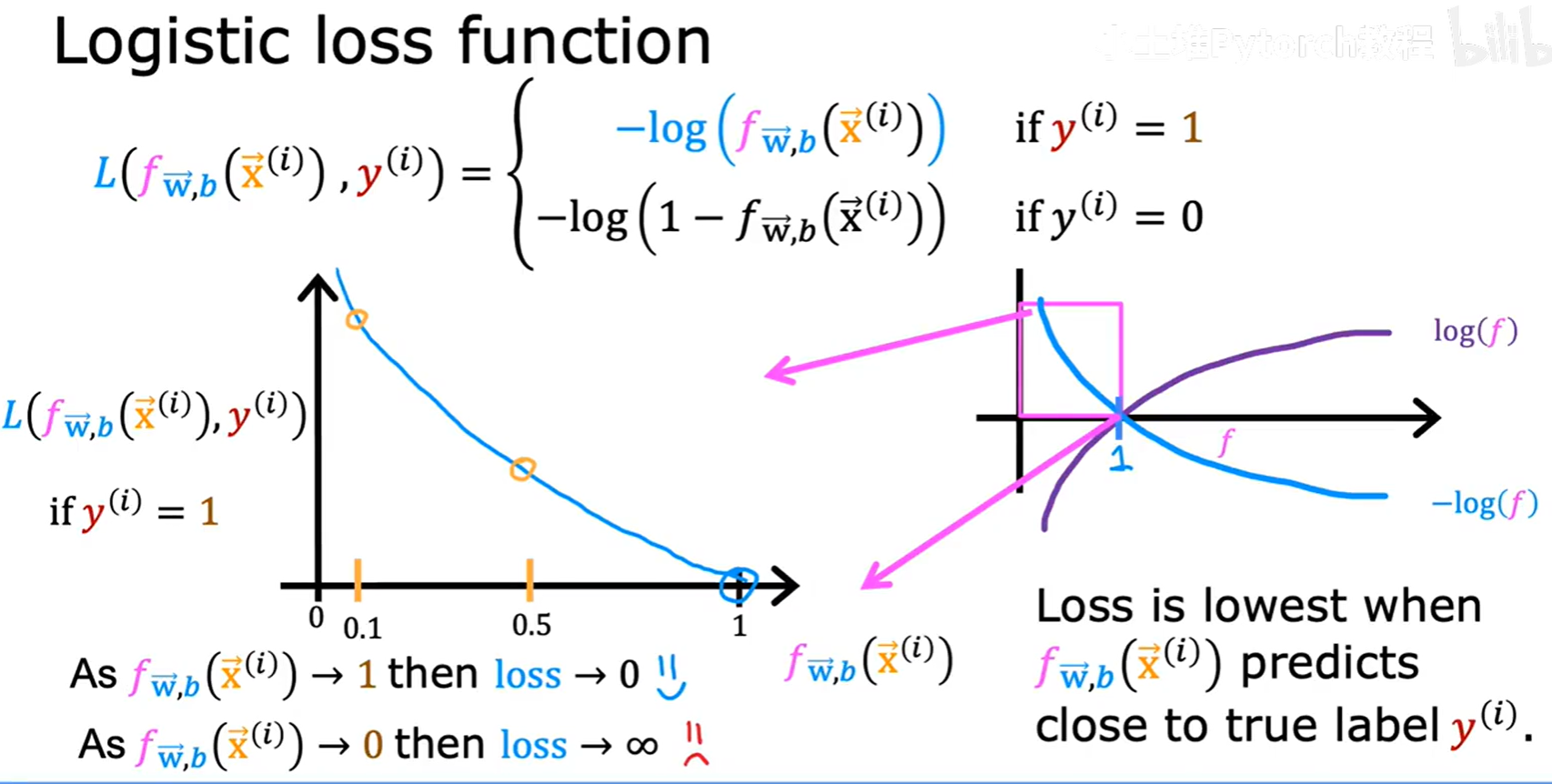
逻辑回归的损失函数定义如下：

• 如果真实标签 y=1: L = -log(f(x))
• 如果真实标签 y=0: L = -log(1 - f(x))

我们来直观地理解这个函数是如何工作的：

3.2.1 当 y=1 时

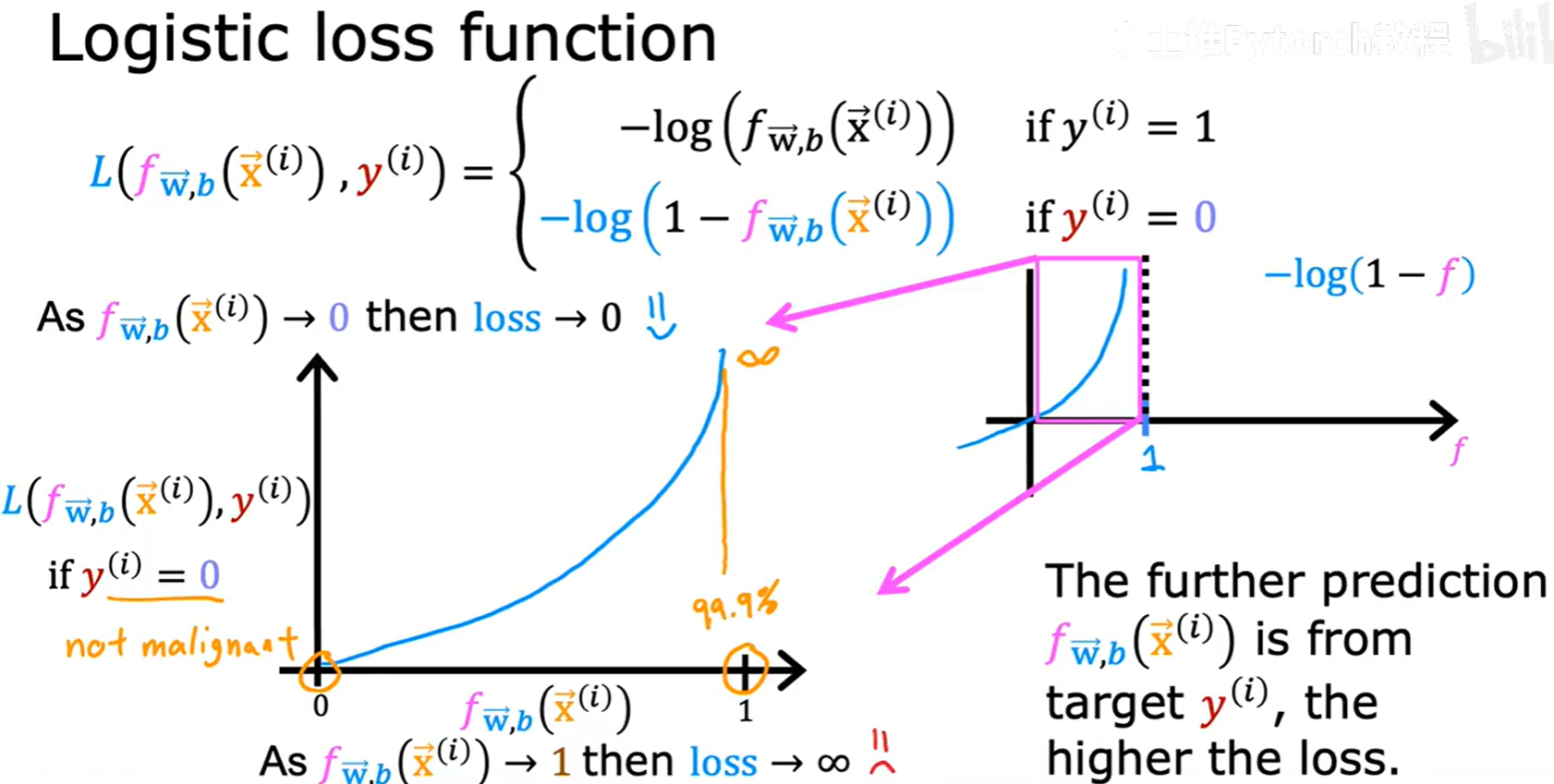
• 如果模型预测 f(x) 趋近于 1（与真实标签一致），那么 -log(f(x)) 的值就趋近于 0。这意味着模型的损失很小，得到了“奖励”。
• 如果模型预测 f(x) 趋近于 0（与真实标签相反），那么 -log(f(x)) 的值会趋近于无穷大。这意味着模型受到了巨大的“惩罚”。

3.2.2 当 y=0 时

• 如果模型预测 f(x) 趋近于 0（与真实标签一致），那么 1-f(x) 趋近于 1，-log(1 - f(x)) 的值就趋近于 0。模型损失很小。
• 如果模型预测 f(x) 趋近于 1（与真实标签相反），那么 1-f(x) 趋近于 0，-log(1 - f(x)) 的值会趋近于无穷大，模型受到巨大惩罚。

这个损失函数的设计非常巧妙，它确保了当模型预测正确时损失接近0，预测错误时损失会急剧增大。

3.3 代价函数与梯度下降

逻辑回归的代价函数 J(w⃗, b) 就是所有训练样本损失的平均值。

J(w⃗, b) = (1/m) * Σ [ L(f(x⁽ⁱ⁾), y⁽ⁱ⁾) ] (从 i=1 到 m)

这个代价函数（也被称为“对数损失”或“交叉熵损失”）被证明是一个凸函数，因此我们可以放心地使用梯度下降来寻找全局最小值。

3.3.1 简化版代价函数

为了便于数学处理，我们可以将分段定义的损失函数用一个等价的式子来表示：

L(f(x), y) = -y * log(f(x)) - (1-y) * log(1 - f(x))

• 当 y=1 时，第二项为0，公式变为 -log(f(x))。
• 当 y=0 时，第一项为0，公式变为 -log(1 - f(x))。

这与我们之前的分段定义完全一致。

将这个简化版的损失函数代入，我们就得到了逻辑回归最终的代价函数表达式：

J(w⃗, b) = -(1/m) * Σ [ y⁽ⁱ⁾log(f(x⁽ⁱ⁾)) + (1-y⁽ⁱ⁾)log(1-f(x⁽ⁱ⁾)) ]

3.3.2 逻辑回归的梯度下降

现在，我们只需要计算出这个新的代价函数对 wⱼ 和 b 的偏导数，就可以应用梯度下降了。

经过微积分推导后，我们得到了一个令人惊讶的简洁结果：
∂/∂wⱼ J(w⃗,b) = (1/m) * Σ [ (f(x⁽ⁱ⁾) - y⁽ⁱ⁾) * xⱼ⁽ⁱ⁾ ]
∂/∂b J(w⃗,b) = (1/m) * Σ [ (f(x⁽ⁱ⁾) - y⁽ⁱ⁾) ]

大家会发现，这个梯度（导数）的表达式，竟然和线性回归的梯度表达式一模一样！

这当然不是巧合，而是背后有更深的数学原理。但对我们来说，这意味着实现梯度下降时，更新参数的代码部分可以完全复用。

唯一的区别在于 f(x) 的定义：

• 在线性回归中： f(x⃗) = w⃗ · x⃗ + b
• 在逻辑回归中： f(x⃗) = 1 / (1 + e⁻⁽ʷ⃗·ˣ⃗⁺ᵇ⁾)

之前我们讨论的所有梯度下降的实践技巧，如监控学习曲线、向量化实现、特征缩放等，同样完全适用于逻辑回归。