当前位置：首页 > news >正文

算法性能的核心度量：时间复杂度与空间复杂度深度解析

news 2025/10/16 11:49:01

🔥 脏脏a的技术站 🔥

「在代码的世界里，脏脏的技术探索从不设限～」

🚀 个人主页：脏脏a-CSDN博客

📌 技术聚焦：时间复杂度和空间复杂度的计算
📊 文章专栏：初阶数据结构

🔗 上篇回顾：

在计算机科学领域，算法是解决问题的核心步骤，而衡量一个算法的优劣绝非仅凭代码简洁度。本文将从算法效率的基本概念出发，系统讲解时间复杂度与空间复杂度的定义、计算方法、常见案例，并结合校招考点与 OJ 实战，帮助读者全面掌握算法性能分析的核心技能。

一、算法效率：不止于 “简洁”

1.1 算法复杂度：时间与空间的双重维度

1.2 校招中的复杂度考察：高频考点梳理

二、时间复杂度：从 “执行次数” 到 “渐进表示”

2.1 时间复杂度的定义

2.2 大 O 渐进表示法：3 步推导规则

2.3 最好、平均与最坏情况：为何关注最坏？

2.4 常见时间复杂度计算：8 个经典案例

案例 1：单循环 + 常数循环（Func2）

案例 2：双变量循环（Func3）

案例 3：常数次循环（Func4）

案例 4：字符串查找（strchr）

案例 5：冒泡排序（BubbleSort）

案例 6：二分查找（BinarySearch）

案例 7：阶乘递归（Fac）

案例 8：斐波那契递归（Fib）

三、空间复杂度：关注 “额外申请的空间”

3.1 空间复杂度计算：3 个经典案例

案例 1：冒泡排序（BubbleSort）

案例 2：斐波那契数组（Fibonacci）

案例 3：阶乘递归（Fac）

3.2 常见空间复杂度对比

四、OJ 实战：复杂度约束下的解题思路

4.1 缺失的第一个正数（LeetCode 41）

4.2 旋转数组（LeetCode 189）

五、总结：算法性能分析的核心要点

一、算法效率：不止于 “简洁”

当我们看到一段简洁的代码时，很容易误以为它是 “好算法”。例如斐波那契数列的递归实现：

long long Fib(int N) {if (N < 3)return 1;return Fib(N-1) + Fib(N-2);
}

这段代码仅 6 行，却存在严重的性能问题 —— 随着 N 增大，运行时间会呈指数级增长。这说明 “简洁” 不等于 “高效”，我们需要更科学的度量标准。

1.1 算法复杂度：时间与空间的双重维度

算法运行时需消耗两类资源：时间资源（CPU 执行时间）和空间资源（内存占用）。因此，衡量算法效率的核心指标是：

时间复杂度：描述算法运行快慢的度量，与基本操作执行次数正相关。
空间复杂度：描述算法所需额外内存的度量，与显式申请的变量 / 空间数量正相关。

在计算机发展早期，内存容量有限，空间复杂度是核心关注点；如今内存成本大幅降低，时间复杂度成为校招与工程中的首要考察对象，但空间复杂度仍需在特定场景（如嵌入式开发、大数据处理）中关注。

1.2 校招中的复杂度考察：高频考点梳理

从腾讯、字节等企业的校招面试题来看，复杂度相关考点贯穿笔试与面试，典型问题包括：

排序算法的时间复杂度（如快排最坏情况 O (n²)、归并排序稳定 O (nlogn)）；
哈希表的 hash 冲突解决（链地址法中链表过长时，查询复杂度从 O (1) 退化到 O (n)）；
OJ 题的复杂度约束（如要求 “时间 O (n)、空间 O (1)”，如《剑指 Offer 56-1：数组中数字出现的次数》）；
递归算法的时间 / 空间复杂度分析（如斐波那契递归、阶乘递归）。

掌握复杂度计算，是通过算法笔试、面试的基础。

二、时间复杂度：从 “执行次数” 到 “渐进表示”

时间复杂度的本质是 “算法基本操作的执行次数与问题规模 N 的数学关系”。由于我们无需精确计算执行次数（如 “1002010 次”），而是关注 “随 N 增长的趋势”，因此引入大 O 渐进表示法来简化描述。

2.1 时间复杂度的定义

时间复杂度是一个函数，定量描述算法的基本操作执行次数。例如，对于以下函数Func1，我们需要先计算其基本操作（++count）的执行次数：

void Func1(int N) {int count = 0;// 外层循环N次，内层循环N次：共N*N次for (int i = 0; i < N; ++i) {for (int j = 0; j < N; ++j) {++count; // 基本操作1}}// 循环2*N次：共2*N次for (int k = 0; k < 2 * N; ++k) {++count; // 基本操作2}// 循环10次：共10次int M = 10;while (M--) {++count; // 基本操作3}printf("%d\n", count);
}

通过计算，Func1的基本操作执行次数为：F(N) = N² + 2N + 10

当 N 取不同值时，F (N) 的结果为：

N=10 → F(N)=130
N=100 → F(N)=10210
N=1000 → F(N)=1002010

可以发现，随着 N 增大，N²项对结果的影响远大于2N和10，因此我们可以忽略次要项，用更简洁的方式描述趋势 —— 这就是大 O 渐进表示法的核心思想。

2.2 大 O 渐进表示法：3 步推导规则

大 O 符号（Big O notation）用于描述函数的渐进行为，即当 N 趋近于无穷大时，执行次数的增长趋势。推导步骤如下：

常数替换：用常数 1 取代所有加法常数（如10→1）；
保留高阶：只保留表达式中最高阶的项（如N² + 2N + 1→N²）；
去除系数：若最高阶项存在且系数不为 1，去除系数（如2N²→N²）。

以Func1为例，F(N)=N²+2N+10→按规则推导后为O(N²)，即Func1的时间复杂度为O(N²)。

2.3 最好、平均与最坏情况：为何关注最坏？

部分算法的执行次数会因输入数据不同而变化，因此存在三种情况：

最好情况：任意输入规模的最小执行次数（如下界）。例如在数组中搜索数据，运气好时 1 次找到；
平均情况：任意输入规模的期望执行次数（如概率平均）。例如搜索数据的平均次数为N/2；
最坏情况：任意输入规模的最大执行次数（如上界）。例如搜索数据时需遍历整个数组，共N次。

在实际工程与校招中，我们优先关注最坏情况—— 因为最坏情况决定了算法的 “最差性能”，是系统设计的安全边界（如服务器需应对峰值负载，而非平均负载）。例如数组搜索的时间复杂度统一表示为O(N)（基于最坏情况）。

2.4 常见时间复杂度计算：8 个经典案例

掌握复杂度计算的关键是 “定位基本操作→分析与 N 的关系→应用大 O 规则”。以下 8 个案例覆盖校招高频场景，结合代码逐一解析：

案例 1：单循环 + 常数循环（Func2）

void Func2(int N) {int count = 0;// 循环2*N次：基本操作执行2N次for (int k = 0; k < 2 * N; ++k) {++count;}// 循环10次：基本操作执行10次（常数）int M = 10;while (M--) {++count;}printf("%d\n", count);
}

基本操作次数：2N + 10；
大 O 推导：常数 10→1，保留最高阶2N，去除系数 2→O(N)；
结论：时间复杂度O(N)。

案例 2：双变量循环（Func3）

void Func3(int N, int M) {int count = 0;// 循环M次：基本操作执行M次for (int k = 0; k < M; ++k) {++count;}// 循环N次：基本操作执行N次for (int k = 0; k < N; ++k) {++count;}printf("%d\n", count);
}

基本操作次数：M + N；
说明：N 和 M 均为独立的问题规模（无明确大小关系），无法合并；
结论：时间复杂度O(N + M)（若题目明确 M≈N，可简化为O(N)）。

案例 3：常数次循环（Func4）

void Func4(int N) {int count = 0;// 循环100次：基本操作执行100次（与N无关）for (int k = 0; k < 100; ++k) {++count;}printf("%d\n", count);
}

基本操作次数：100（常数，与 N 无关）；
大 O 推导：常数 100→1→O(1)；
结论：时间复杂度O(1)（注：O(1)表示常数级，非 “1 次”）。

案例 4：字符串查找（strchr）

strchr函数功能：在字符串str中查找字符character，找到则返回地址，否则返回 NULL。

const char * strchr (const char * str, int character);

基本操作：遍历字符串的每个字符（比较操作）；
最好情况：1 次（首字符匹配）；
最坏情况：N 次（末字符匹配或无匹配，N 为字符串长度）；
结论：时间复杂度O(N)（基于最坏情况）。

案例 5：冒泡排序（BubbleSort）

冒泡排序的核心是 “相邻元素比较交换，每轮将最大元素沉底”，代码如下：

void BubbleSort(int* a, int n) {assert(a);for (size_t end = n; end > 0; --end) {int exchange = 0;// 每轮比较次数：end-1次（end从n递减到1）for (size_t i = 1; i < end; ++i) {if (a[i-1] > a[i]) {Swap(&a[i-1], &a[i]);exchange = 1;}}if (exchange == 0) // 无交换，数组已有序，提前退出break;}
}

基本操作：比较与交换（核心为比较次数）；
最好情况：N-1次（数组已有序，1 轮遍历后退出）→O(N)；
最坏情况：(N-1)+...+1 = N(N+1)/2次（数组逆序，需 N-1 轮遍历）→按大 O 规则简化为O(N²)；
结论：时间复杂度O(N²)（基于最坏情况）。

案例 6：二分查找（BinarySearch）

二分查找仅适用于 “有序数组”，核心是 “每次将搜索范围缩小一半”，代码如下：

int BinarySearch(int* a, int n, int x) {assert(a);int begin = 0;int end = n-1;while (begin < end) {int mid = begin + ((end - begin) >> 1); // 避免溢出，等价于(begin+end)/2if (a[mid] < x)begin = mid + 1;else if (a[mid] > x)end = mid;elsereturn mid; // 找到目标}return -1; // 未找到
}

基本操作：比较a[mid]与x（每次循环 1 次比较）；
核心逻辑：搜索范围从n→n/2→n/4→...→1，设比较次数为k，则n/(2^k) ≥ 1→k ≤ log₂n；
最好情况：1 次（中间元素即目标）；
最坏情况：log₂n次（目标在边界或无目标）；
结论：时间复杂度O(logN)（算法分析中logN默认以 2 为底，可写作log₂N或lgN）。

案例 7：阶乘递归（Fac）

递归算法的时间复杂度需分析 “递归调用次数” 与 “每次调用的基本操作次数”，阶乘递归代码如下：

long long Fac(size_t N) {if (0 == N)return 1; // 终止条件return Fac(N-1) * N; // 递归调用 + 乘法操作（基本操作）
}

递归调用链：Fac(N-1)→...→Fac(0)，共N次调用；
每次调用的基本操作：1 次乘法，总基本操作次数≈N；
结论：时间复杂度O(N)。

案例 8：斐波那契递归（Fib）

斐波那契递归的调用关系呈 “二叉树” 结构，代码如下：

long long Fib(size_t N) 
{if (N < 3)return 1; // 终止条件（N=1或2时返回1）return Fib(N-1) + Fib(N-2); // 两次递归调用 + 加法操作
}

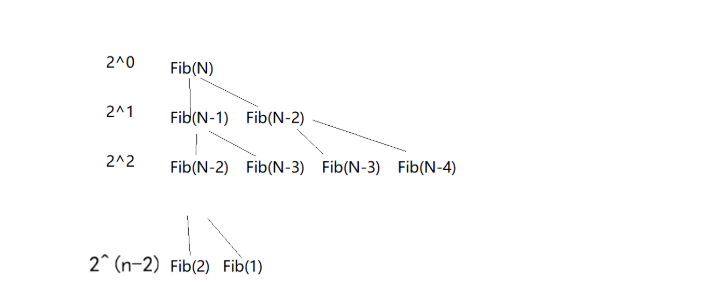
输入规模为N时，递归调用两次，输入规模为N-1时，递归调用4次，依次类推，N=3时，递归调用结束，结果为：2^0 + 2^1 + ...... 2^(n-2) = 2^（N-1）-1
结论：时间复杂度O(2^N)（指数级复杂度，N≥30 时运行会严重卡顿）。

三、空间复杂度：关注 “额外申请的空间”

空间复杂度是对算法运行时临时占用额外存储空间的度量，同样使用大 O 渐进表示法。需注意：

空间复杂度计算的是 “额外空间”，而非程序总空间（如输入数据的空间不计算在内）；
函数运行时的栈空间（如参数、局部变量、寄存器信息）在编译时已确定，因此仅需统计显式申请的额外空间（如动态内存分配、数组扩容）。

3.1 空间复杂度计算：3 个经典案例

案例 1：冒泡排序（BubbleSort）

void BubbleSort(int* a, int n) {assert(a);for (size_t end = n; end > 0; --end) {int exchange = 0; // 局部变量（常数空间）for (size_t i = 1; i < end; ++i) {if (a[i-1] > a[i]) {Swap(&a[i-1], &a[i]); // 交换函数若用临时变量，仍为常数空间exchange = 1;}}if (exchange == 0)break;}
}

额外空间：仅使用exchange等局部变量（常数个，与 N 无关）；
结论：空间复杂度O(1)。

案例 2：斐波那契数组（Fibonacci）

该函数通过动态内存分配申请数组，存储斐波那契数列的前n项

long long* Fibonacci(size_t n) {if (n == 0)return NULL;// 显式申请n+1个long long的空间（与n正相关）long long *fibArray = (long long *)malloc((n+1) * sizeof(long long));fibArray[0] = 0;fibArray[1] = 1;for (int i = 2; i <= n; ++i) {fibArray[i] = fibArray[i-1] + fibArray[i-2];}return fibArray;
}

额外空间：动态申请的fibArray数组，大小为n+1（与 N 成正比）；
结论：空间复杂度O(N)。

案例 3：阶乘递归（Fac）

递归算法的空间复杂度需分析 “递归栈的深度”（即递归调用的最大层数）：

long long Fac(size_t N) {if (N == 0)return 1;return Fac(N-1) * N;
}

递归栈深度：调用链Fac(N)→Fac(N-1)→...→Fac(0)，最大层数为N+1（与 N 成正比）；
额外空间：递归栈帧（存储参数、返回地址等），每个栈帧占常数空间，总空间与栈深度成正比；
结论：空间复杂度O(N)。

3.2 常见空间复杂度对比

与时间复杂度类似，空间复杂度也有不同的增长级别，按效率从高到低排序如下：

表达式	大 O 表示	复杂度级别	适用场景
5（常数）	O(1)	常数阶	原地排序（如冒泡、快排）
3N+2	O(N)	线性阶	动态数组、单链表存储
2logN	O(logN)	对数阶	二分查找的递归栈（非迭代版）
NlogN	O(NlogN)	NlogN 阶	归并排序的临时数组
N²	O(N²)	平方阶	二维数组存储（如邻接矩阵）

四、OJ 实战：复杂度约束下的解题思路

校招算法笔试中，OJ 题通常会明确时间 / 空间复杂度约束，需结合复杂度分析设计解法。以下以两道经典题为例，讲解解题思路。

4.1 缺失的第一个正数（LeetCode 41）

【题目描述】：

给你一个未排序的整数数组nums，请找出其中没有出现的最小的正整数。要求：时间复杂度O(n)，空间复杂度O(1)。

【示例】：

输入：[3,0,1] → 输出：2（缺失的最小正整数为 2）；
输入：[9,6,4,2,3,5,7,0,1] → 输出：8。

【思路分析】：

约束分析：时间O(n)意味着不能用排序（排序最少O(nlogn)），空间O(1)意味着不能用哈希表（哈希表需O(n)空间）；
核心思想：利用原数组原地标记—— 将数值为x的元素放到索引x-1的位置（如数值 1 放到索引 0，数值 2 放到索引 1），最后遍历数组，找到第一个索引i与数值i+1不匹配的位置，i+1即为答案。

【代码片段】：

class Solution {
public:int missingNumber(vector<int>& nums) {// 按位异或规律：a^a=0，a^0=aint val = 0;// 第一次循环：异或 0 到 nums.size()（因为 nums 是 0 到 n-1 缺失一个，所以范围是 0 到 n）for (int i = 0; i <= nums.size(); i++) {val = val ^ i;}// 第二次循环：异或数组中的所有元素for (int i = 0; i < nums.size(); i++) {val = val ^ nums[i];}return val;}
};

4.2 旋转数组（LeetCode 189）

【题目描述】：

给定一个整数数组nums，将数组中的元素向右轮转k个位置（k是非负数）。要求：设计至少两种解决方案，其中一种空间复杂度为O(1)。

【示例】：

输入：nums = [1,2,3,4,5,6,7], k = 3 → 输出：[5,6,7,1,2,3,4]。

思路 1：使用额外数组（空间 O (n)）

核心思想：将原数组的n-k到n-1位置的元素放到新数组的开头，0到n-k-1位置的元素放到新数组的末尾；
缺点：空间复杂度O(n)，不满足最优空间约束。

思路 2：三次反转（空间 O (1)）

核心思想：通过反转操作实现原地旋转，步骤如下：
1. 反转整个数组：[1,2,3,4,5,6,7]→[7,6,5,4,3,2,1]；
2. 反转前k个元素：[7,6,5,4,3,2,1]→[5,6,7,4,3,2,1]；
3. 反转后n-k个元素：[5,6,7,4,3,2,1]→[5,6,7,1,2,3,4]；
优点：空间复杂度O(1)，时间复杂度O(n)（反转操作共遍历数组 2 次）。

【代码片段（三次反转）】：

void reverse(int* nums, int left, int right) {while (left < right) {int temp = nums[left];nums[left] = nums[right];nums[right] = temp;left++;right--;}
}void rotate(int* nums, int numsSize, int k) {k %= numsSize; // 处理k >= numsSize的情况reverse(nums, 0, numsSize-1); // 整体反转reverse(nums, 0, k-1); // 反转前k个reverse(nums, k, numsSize-1); // 反转后n-k个
}