【基础算法】BFS

一、BFS

广度优先搜索（Breadth-First Search, BFS） 是一种经典的搜索算法。我们最早学习到的 BFS 应该是二叉树的层序遍历，其中我们要用到的一个核心数据结构就是队列。

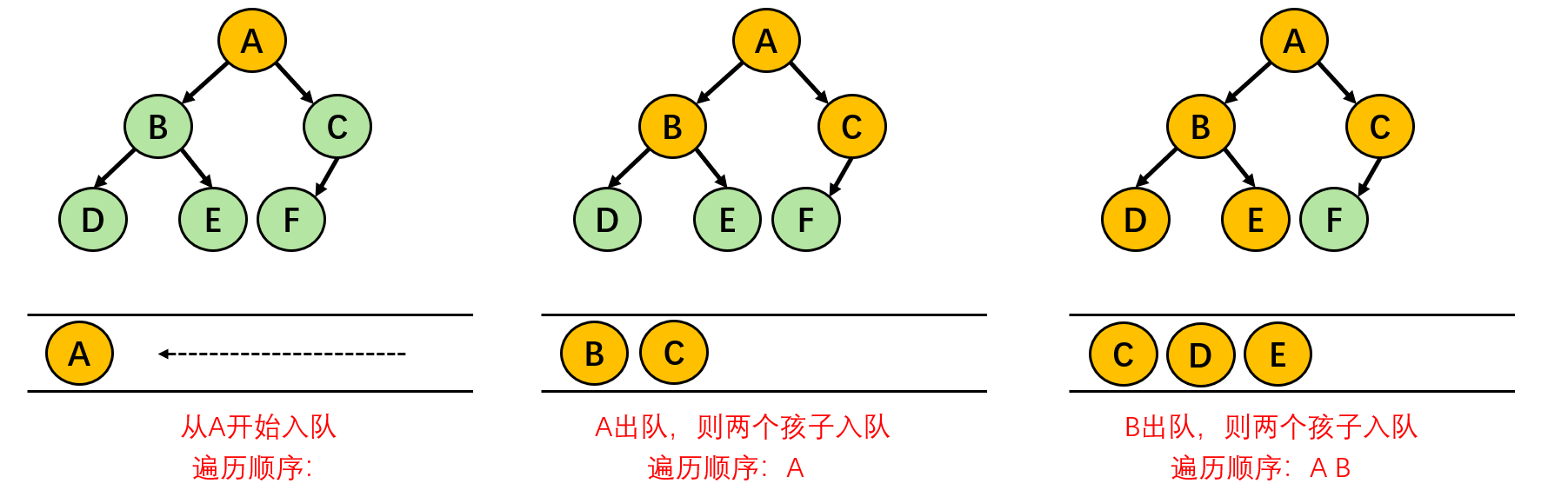
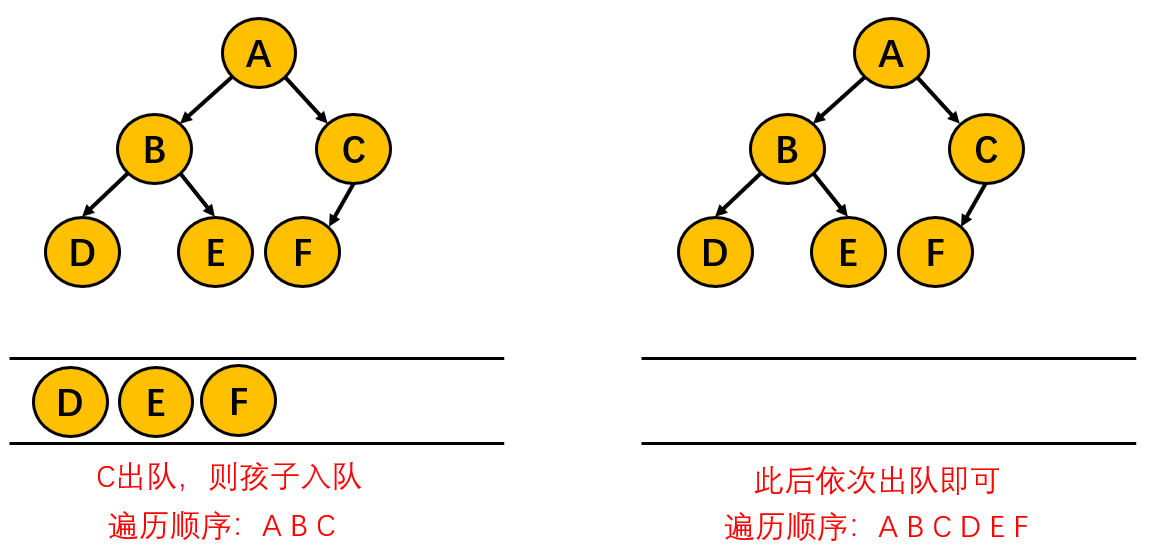
宽度优先搜索的过程中，每次都会从当前点向外扩展一层，所以会具有一个最短路的特性（从下面的题目中可以感受到）。因此，宽搜不仅能搜到所有的状态，还能找出起始状态距离某个状态的最小步数。 但是，前提条件是每次扩展的代价都是 1，或者都是相同的数。因此，宽搜常常被用于解决边权为 1 的最短路问题。

---

二、OJ 练习

1. 马的遍历 ⭐⭐

【题目连接】

P1443 马的遍历 - 洛谷

【题目描述】

有一个 $n\times m$ 的棋盘，在某个点 $(x,y)$ 上有一个马，要求你计算出马到达棋盘上任意一个点最少要走几步。

【输入格式】

输入只有一行四个整数，分别为 $n,m,x,y$。

【输出格式】

一个 $n\times m$ 的矩阵，代表马到达某个点最少要走几步（不能到达则输出 $-1$）。

输入

3 3 1 1

输出

0 3 2    
3 -1 1    
2 1 4

【说明/提示】

对于全部的测试点，保证 $1\le x\le n\le 400$，$1\le y\le m\le 400$。

2022 年 8 月之后，本题去除了对输出保留场宽的要求。为了与之兼容，本题的输出以空格或者合理的场宽分割每个整数都将判作正确。

---

(1) 解题思路

这道题问的是最少需要走多少步，我们知道 BFS 是一种逐层扩展的算法，能够保证首先访问距离起点最近的点，适合求解最短路径问题。

我们可以从起点开始，将起点距离标记为 0，并加入队列。然后，每次从队列中取出一个点，检查所有8个移动方向。对于每个新位置，如果它在棋盘范围内且未被访问过，则更新其距离为当前点距离加1，并加入队列。这个过程持续到队列为空，确保所有可达点都被计算。

---

(2) 代码实现

#include<iostream>
#include<queue>
#include<cstring>using namespace std;const int N = 410;
int dis[N][N];  // 记录从起点开始走到每个点需要的最少步数int n, m, x, y;// 对应 8 个方向
int dx[] = {1, 2, 2, 1, -1, -2, -2, -1};
int dy[] = {2, 1, -1, -2, -2, -1, 1, 2};void bfs()
{queue<pair<int, int>> q;q.push({x, y});dis[x][y] = 0;  // 起点距离设置为 0while(!q.empty()){int r = q.front().first;int c = q.front().second;q.pop();// 枚举 8 个方向for(int i = 0; i < 8; i++){int rr = r + dx[i];int cc = c + dy[i];// 如果新的位置合法并且没有走到过if(rr > 0 && rr <= n && cc > 0 && cc <= m && dis[rr][cc] == -1){q.push({rr, cc});dis[rr][cc] = dis[r][c] + 1;}}}
}int main()
{cin >> n >> m >> x >> y;// 还没有走到的位置设置为 -1memset(dis, -1, sizeof(dis));bfs();for(int i = 1; i <= n; i++){for(int j = 1; j <= m; j++){cout << dis[i][j] << " ";}cout << endl;}return 0;
}

---

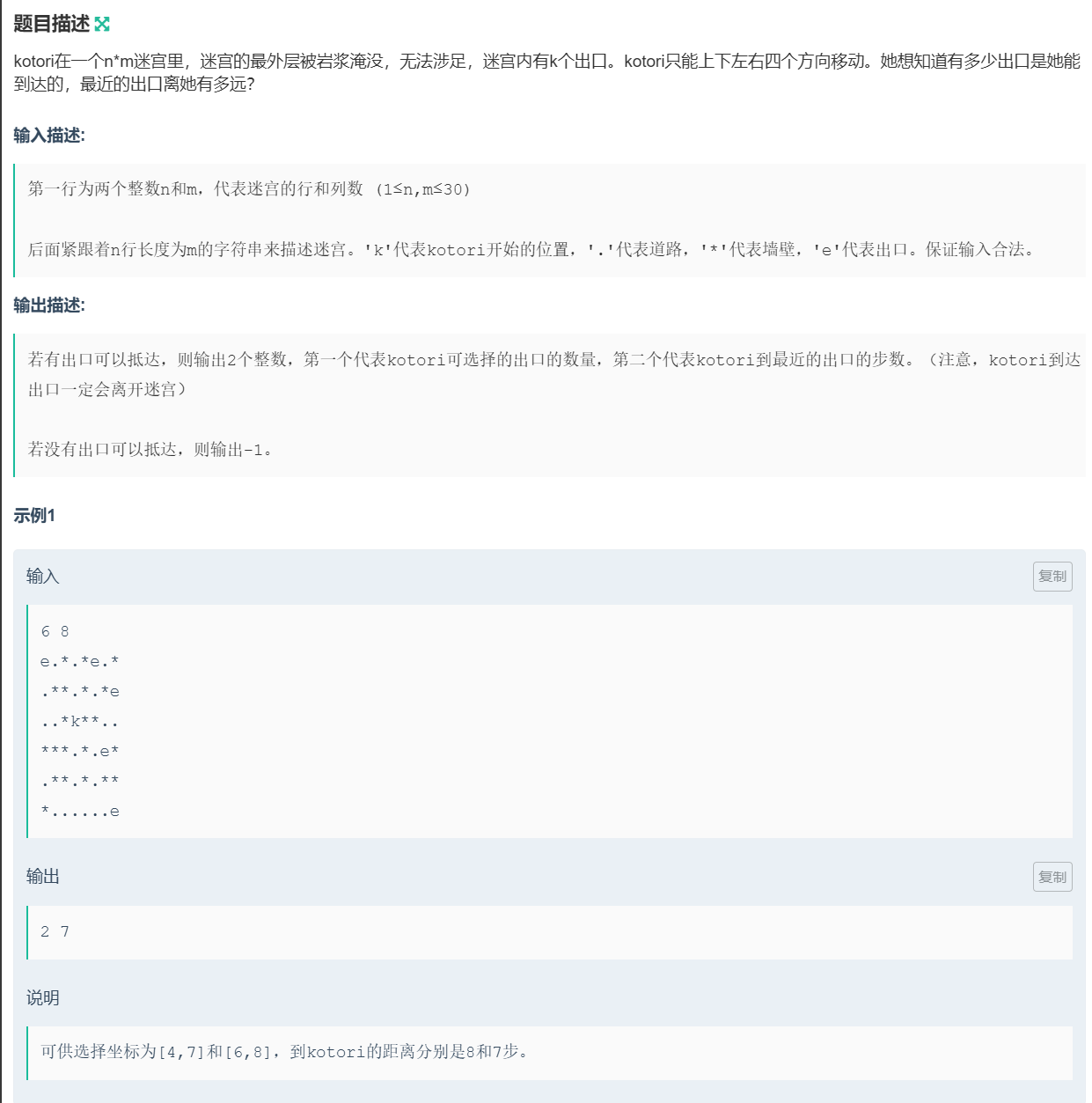
2. kotori 和迷宫 ⭐⭐

【题目链接】

kotori和迷宫

---

(1) 解题思路

从起点位置开始向四个方向逐层扩展，走到过的位置就把它置为 *，下次就不能再走了。由于需要记录到达最近出口的步数以及出口的数量，所以这里我设置了两个变量 flag 和 step，step 用于记录最近出口的步数，都初始化为 0。当遇到出口时就将 flag 赋值为 1。而只有当 flag 为 0 的时候向外扩 step 才 ++。

---

(2) 代码实现

#include<iostream>
#include<queue>using namespace std;typedef pair<int, int> PII;
const int N = 35;
char mat[N][N];  // 迷宫
int cnt, step;   // 出口数量和最近出口的距离 
int n, m, flag;// 对应 4 个方向
int dx[] = {0, 0, -1, 1};
int dy[] = {1, -1, 0, 0};void bfs(int x, int y)
{queue<PII> q;q.push({x, y});mat[x][y] = '*';while(!q.empty()){int t = q.size();if(flag == 0) step++;// 每一个 while 循环代表 BFS 遍历的每一“层”while(t--){int r = q.front().first;int c = q.front().second;q.pop();// 枚举 4 个方向for(int i = 0; i < 4; i++){int rr = r + dx[i];int cc = c + dy[i];// 当新的位置合法并且没有走过才去这个位置if(rr > 0 && rr <= n && cc > 0 && cc <= m && mat[rr][cc] != '*'){// 如果出口，那么不加入队列，更新 cnt 和 flagif(mat[rr][cc] == 'e'){mat[rr][cc] = '*';cnt++;flag = 1;}// 如果是路，那么加入队列else{q.push({rr, cc});mat[rr][cc] = '*';}}}}}
}int main()
{int x, y;cin >> n >> m;for(int i = 1; i <= n; i++){for(int j = 1; j <= m; j++){cin >> mat[i][j];if(mat[i][j] == 'k'){x = i;y = j;}}}bfs(x, y);if(cnt) cout << cnt << " " << step;else cout << -1 << endl;return 0;
}

---

3. Catch That Cow S ⭐⭐

【题目链接】

[P1588 USACO07OPEN] Catch That Cow S - 洛谷

【题目描述】

FJ 丢失了他的一头牛，他决定追回他的牛。已知 FJ 和牛在一条直线上，初始位置分别为 $x$ 和 $y$，假定牛在原地不动。FJ 的行走方式很特别：他每一次可以前进一步、后退一步或者直接走到 $2\times x$ 的位置。计算他至少需要几步追上他的牛。

【输入格式】

第一行为一个整数 $t(1\le t\le 10)$，表示数据组数；

接下来每行包含一个两个正整数 $x,y(0<x,y\le 10^5)$，分别表示 FJ 和牛的坐标。

【输出格式】

对于每组数据，输出最少步数。

【示例一】

输入

1 
5 17

输出

4

---

(1) 解题思路

这道题乍一看会想到贪心，但是怎么贪怎么不对劲。我们不妨直接暴力枚举。对于每一个数我们都枚举出它 +1、-1 和 *2 之后的结果，如下：

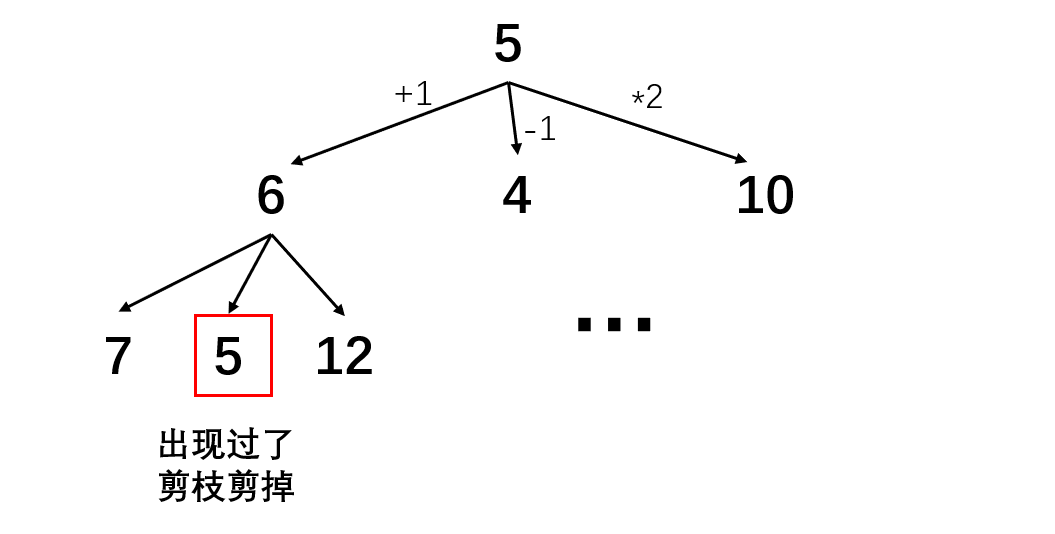
相当于我们就是对这一棵多叉树进行层序遍历，同时记录步数（层数）。为了优化时间复杂度，我们把出现过的数字剪掉。如果出现最终结果，返回步数即可。这里的步数一定就是最少步数，这也是 BFS 的特性。

---

(2) 代码实现

#include<iostream>
#include<cstring>
#include<queue>using namespace std;const int N = 1e5 + 10;
bool vis[N];  // 记录某个数是否出现过int bfs(int x, int y)
{int step = 0;queue<int> q;q.push(x);vis[x] = true;while(1){int len = q.size();while(len--){int n = q.front();q.pop();if(n == y) return step;int tmp = n;// 枚举 +1，-1，*2n = tmp + 1;if(n > 0 && n < N && !vis[n]){q.push(n);vis[n] = true;}n = tmp - 1;if(n > 0 && n < N && !vis[n]){q.push(n);vis[n] = true;}n = tmp * 2;if(n > 0 && n < N && !vis[n]){q.push(n);vis[n] = true;}}step++;  }
}int main()
{int t; cin >> t;while(t--){memset(vis, false, sizeof(vis));int x, y; cin >> x >> y;cout << bfs(x, y) << endl;}return 0;
}

---

4. 八数码难题 ⭐⭐⭐

【题目链接】

P1379 八数码难题 - 洛谷

【题目描述】

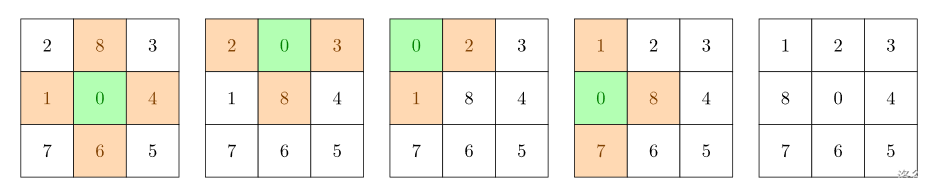
在 $3\times 3$ 的棋盘上，摆有八个棋子，每个棋子上标有 $1$ 至 $8$ 的某一数字。棋盘中留有一个空格，空格用 $0$ 来表示。空格周围的棋子可以移到空格中。要求解的问题是：给出一种初始布局（初始状态）和目标布局（为了使题目简单,设目标状态为 $123804765$），找到一种最少步骤的移动方法，实现从初始布局到目标布局的转变。

【输入格式】

输入初始状态，一行九个数字，空格用 $0$ 表示。

【输出格式】

只有一行，该行只有一个数字，表示从初始状态到目标状态需要的最少移动次数。保证测试数据中无特殊无法到达目标状态数据。

【示例一】

输入

283104765

输出

4

【说明/提示】

样例解释

图中标有 $0$ 的是空格。绿色格子是空格所在位置，橙色格子是下一步可以移动到空格的位置。如图所示，用四步可以达到目标状态。

并且可以证明，不存在更优的策略。

---

(1) 解题代码

和上一道题 Catch That Cow 一样，看似这道题不知道该如何下手，其实玄机都隐藏在了 “需要的最少移动次数” 上，这也是一道 BFS 问题。我们可以从开始状态枚举空位置与上、下、左、右四个位置交换后的结果并加入到队列中，对于每一个新的结果，只要它不是最终我们想要的状态，我们就继续枚举每个状态中空位置与上下左右交换后的状态，直到遇到我们想要的状态。最终这也就变成了对一棵 “四叉树” 进行层序遍历。

而为了优化时间复杂度，这里把每个遇到的状态都放在一个 unordered_set 里记录下来，以防重复计算。还有有一个关键的点，这道题把一个 3*3 的矩阵转换成了字符串，但是如何计算出我们交换后的字符串呢？

注意到，对于一个字符串中的下标 index，它所对应的矩阵中的位置是 [index / 3, index % 3]；而对于一个矩阵中的位置 [x, y]，它所对应的字符串中的下标为 3 * x + y。这样我们就实现了一维和二维坐标的转换。

---

(2) 代码实现

#include<iostream>
#include<unordered_set>
#include<queue>using namespace std;const string target = "123804765";
int step;int dx[] = {0, 0, -1, 1};
int dy[] = {1, -1, 0, 0};int bfs(string start)
{queue<string> q;q.push(start);unordered_set<string> vis;vis.insert(start);while(1){int len = q.size();while(len--){string t = q.front();q.pop();if(t == target) return step;int index = 0;for(int i = 0; i < 9; i++){if(t[i] == '0') index = i;}int r = index / 3;int c = index % 3;for(int i = 0; i < 4; i++){int rr = r + dx[i];int cc = c + dy[i];if(rr >= 0 && rr < 3 && cc >= 0 && cc < 3){int index2 = rr * 3 + cc;string ss = t;swap(ss[index], ss[index2]);if(!vis.count(ss)){q.push(ss);vis.insert(ss);}}}}step++;}
}int main()
{string start;cin >> start;cout << bfs(start) << endl;return 0;
}