leetcode二分查找(C++)
目录
1.二分查找算法介绍
2.二分查找
3.在排序数组中查找元素的第一个和最后一个位置
4.x的平方根
5.搜索插入位置
6.山脉数组的峰顶索引
7.寻找峰值
8.寻找旋转排序数组中的最小值
9.丢失的数字
1.二分查找算法介绍
特点:细节最多,最容易写出死循环的算法
该算法除了数组有序的情况外,数组无序但是元素有规律也可以使用
二分查找可以有模板,但千万不要死记硬背,理解怎么用什么时候用才是关键
……代表每道题都会有微小的差异,要视情况而定
- 模板1:朴素的二分模板
while(left <= right)
{
int mid = left + (right - left) / 2;
if(……) right = mid - 1;
else if(……) left = mid + 1;
else return ……;
}
- 模板2:查找左边界的二分模板
while(left<right)
{
int mid = left+(right-left)/2;
if(……) left = mid+1;
else right = mid;
}
- 模板3:查找右边界的二分模板
while(left<right)
{
int mid = left+(right-left+1)/2;
if(……) left = mid;
else right = mid - 1;
}
记忆方法:下减1上加1,否则就在中间加1
何为二段性?
数组中一段数据全都满足特性1,另一段数据全都满足特性2,且特性1≠特性2,这就是二段性;换言之,可以把数组or一组数据根据某种特性划分为左右两端,就是二段性的特点
也可以把一段数据换成某一数据,即只要数组中的数据有且仅有2种特性,那么也可以视为二段性,比如下面的第7小节 “寻找峰值” 题目
2.二分查找

最最基础的二分查找算法题,不过多解释
如果可以把整个数组划分为有效区间、无效区间两段(我们称之为“二段性”),那么就可以使用二分查找算法来解决
解题思路:
- x < t -> left = mid + 1 -> [mid+1 , right]
- x > t -> right = mid - 1 -> [left , mid-1]
- x == t -> return
细节问题:
- 循环结束的条件为 left > right ,此时 left 都在 right 右边了,继续循环下去 right 情何以堪;恰好相等的时候,就代表最坏的情况,即left、right一起指向的结果为最终返回值
- 正确性证明:以下图为例,我们比较一次就相当于把 1、2、3 都给比较了,4 < 5 同时 1、2、3 < 4,所以4不能作为答案的时候,1、2、3肯定也不能作为答案
- 每次找 mid 应该是 left + (right - left) / 2,有效区间起始点 + 有效区间中间点 才为mid
- 二分查找算法,每次可以删去一半无效结果;所以对于 N 个元素来说,N/2/2/2/…… = 1,最多执行
次就能解决问题,即时间复杂度为 O(logN)
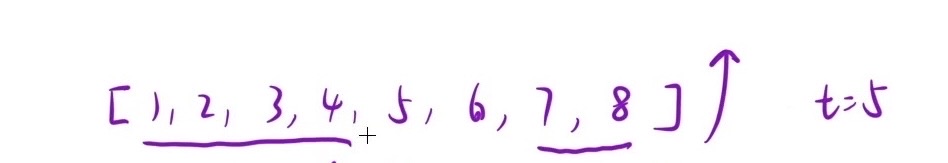
代码:
class Solution {
public:int search(vector<int>& nums, int target) {int left = 0,right = nums.size()-1 ;while(left<=right){int mid = left + (right - left)/2;if(nums[mid] == target) return mid;else if(nums[mid] < target) left = mid + 1;else right = mid - 1;}return -1;}
};3.在排序数组中查找元素的第一个和最后一个位置

在有序数组中,找到 target 值元素的起始、截止位置,如果找不到就返回 -1,-1
查找区间左端点:
1.暴力查找:从数组首元素开始遍历,逐一比较找到起始位置begin,然后再从begin位置开始寻找到截止位置end,最坏情况为 O(N)
2.二分查找:该题不能用朴素二分查找解决,因为朴素二分查找只能找到其中一个target值的元素,但对于该元素在target值元素区间的什么位置不能确定;即使可以找到target值以后,搞一个begin往其前面走,搞一个end往其后面走;但碰到了数组中所有元素都是target值的情况,时间复杂度又变回了 O(N)
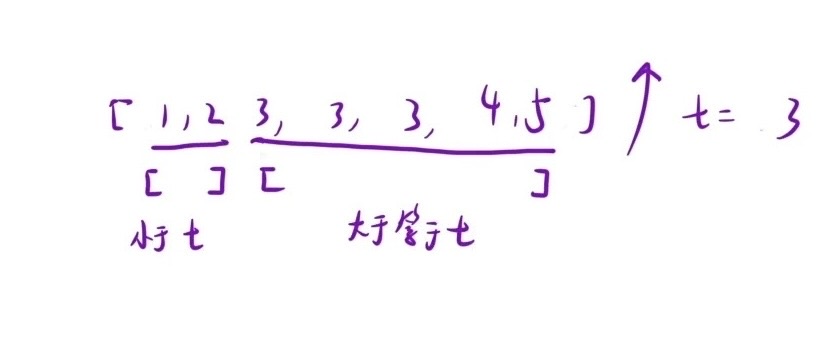
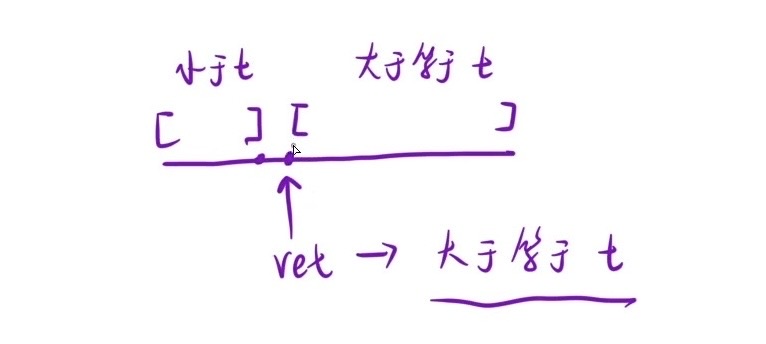
进阶二分查找:先找到以target值(后面简称为t)为元素的区间左端点,并以此为界限划分出 < t and >= t 的两段(如上图所示,符合二段性要求),x 为 mid 下标处的元素值
- x < t -> left = mid + 1 -> [mid+1,right] ;当 x < t 时,区间左端点一定在其右侧,因此直接按照朴素二分的方法,left = mid + 1 即可
- x >= t -> right = mid -> [left,mid] ;当 x >= t 时,区间左端点可能在其左侧,也可能其本身就是左端点;因此 right 不能为 mid - 1 ,right 为 mid - 1 有可能 right 直接到 < t 的区间里了(当 x 恰好为左端点时)
通过上面的划分,right会一直都在有效区间移动(不会超出区间左端点),left会一直在无效区间移动,现在会有以下3种情况:
- left、right两者相遇的时候,即为目标区间(以t值为元素的区间)的左端点
- 数组中所有元素都大于 t 时,会没有左边的无效值区间,相遇时left、right都指向数组首元素,此时只需要判断数组首元素
- 数组中所有元素都小于 t 时,会没有右边的有效值区间,left、right都指向数组最后一个元素,此时只需要判断数组最后一个元素
因此,通过上面的那种划分查找方式,一定能够找到目标区间左端点
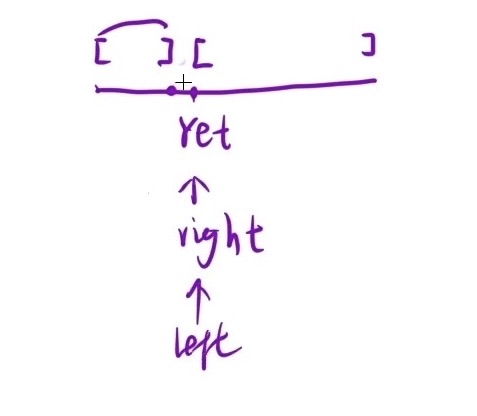
情况1

情况2
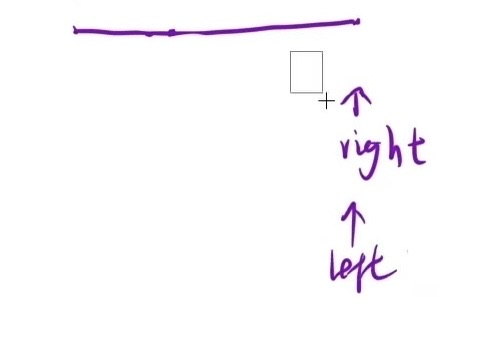
情况3
细节问题:
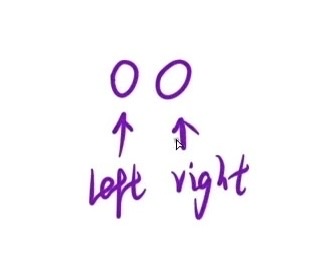
循环条件为 left < right ,千万不要 left <= right ,会陷入死循环;先是 left == right 时即为结果,没必要再进循环判断一次;同时以情况1为例,right、left和mid都指向了ret,ret 是 == t 的,所以会执行 right = mid 这条语句,mid 指向了 right ,所以转换一下就相当于 right = right,因此会陷入死循环
求中点时只能是 left + (right - left) / 2 ,不能是 left + (right - left + 1) / 2;以下图为例(进行最后一次操作时or数组只有两个元素),第一次循环 mid = 0 + 1 = 1,当 x >= t 时,那么right和mid都指向第二个元素;然后第二次循环 mid = 0 + 1 = 1,x 依旧 >= t,right、mid还是指向第二个元素;所以用后面一种方法求中点会导致死循环,千万别用!!!用前面一种办法,mid = 0 + 0 = 0,直接从根源上解决问题
查找区间右端点:
当我们查找完区间左端点后,再去把区间右端点找到就相当于把整个target值区间找到了
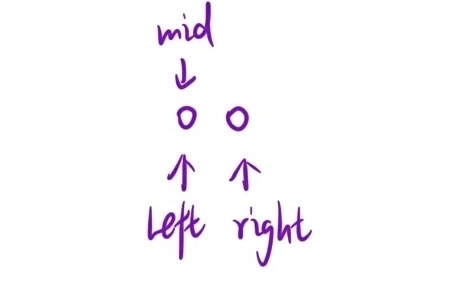
依旧2段,一段 <= t 一段 > t ;当 x <= t 时,右端点在left的右边或为left本身,因此 left = mid;当 x > t 时,右端点在 right 左边,right = mid - 1
循环条件依旧为 left < right ,left == right 时 left 可能会陷入死循环
求中点的方式只能是 left + (right - left + 1) / 2,不能是 left + (right - left) / 2 ;以下图为了,mid = 0 left = 0时,mid = 0 + (1 - 0) / 2 = 0 , 所以会陷入死循环
通过寻找区间左右端点,相当于执行了2次二分查找算法,因此最坏情况下执行
次操作,时间复杂度依旧控制在了 O(logN)
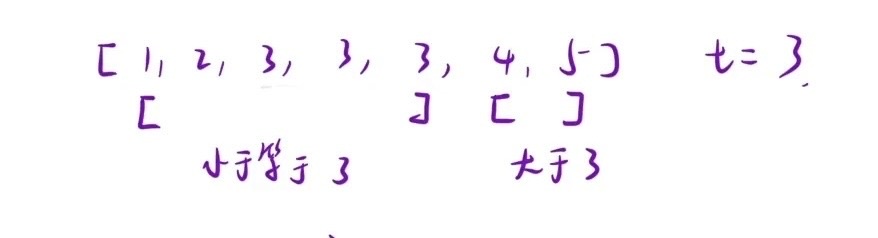
代码:
class Solution {
public:vector<int> searchRange(vector<int>& nums, int target) {if(!nums.size()) return {-1,-1};int left = 0,right = nums.size()-1;int start = -1,end = -1;//查找区间左端点while(left<right){int mid = left+(right-left)/2;if(nums[mid]<target) left = mid+1;else right = mid;}//当 left == right 退出循环之后,判断该值是否为有效值if(nums[left]==target) start = left;//查找区间右端点left = 0 ,right = nums.size()-1;while(left<right){int mid = left+(right-left+1)/2;if(nums[mid]<=target) left = mid;else right = mid - 1;}if(nums[left]==target) end = left;return {start,end};}
};4.x的平方根

自主实现sqrt函数,不用保留小数部分
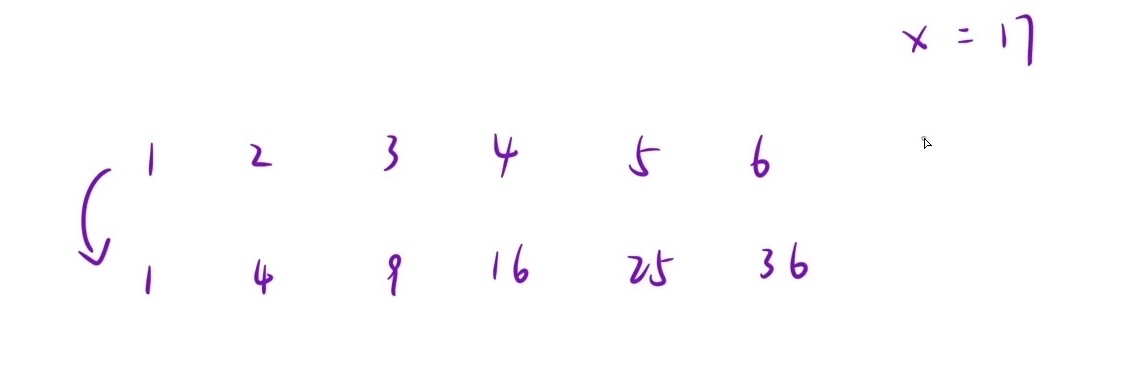
1.暴力解法:以上图为例(x = 17),从以1->x为可能结果的平方值依次尝试,最后发现结果在[4,5]之间,最后返回4为结果
2.二分查找:分为2段,一段ret值平方后的结果 <= x (1->4),一段ret值平方后的结果 > x (5->x);左边作为有效区间,右边作为无效区间,使用寻找右边界的模板
代码:
class Solution {
public:long mySqrt(int x) {long left=0,right=x;while(left<right){long mid = left+(right-left+1)/2;if(mid*mid <= x) left = mid;else right = mid - 1;}return left;}
};代码易错点:类型溢出错误,建议把所有的int都换成long
5.搜索插入位置

查找一个有序数组的target值。如果存在直接返回下标位置,如果不存在就在不影响数组有序的条件下,返回它的插入位置
分为2段,一段小于t,一段大于等于t;ret为右区间的左端点,ret值无论比target大还是恰好为target,都可以作为结果返回;例如例一、例二,ret == 2(下标) 时返回正好是target的下标位置,ret == 1(下标,nums[ret]==3 > 2) 时返回正好是target插入位置;如果用一段小于等于t,一段大于t的方式来划分,那么正好为target值时返回ret,比target值小时要返回ret + 1,比较麻烦
极端情况:当target比数组最小元素要小时,返回ret(此时 ret == 0 ),没有问题;当target比数组最大元素要大时,返回ret(此时 ret == nums.size() - 1),因此需要特判
代码:
class Solution {
public:int searchInsert(vector<int>& nums, int target) {int left=0,right=nums.size()-1;if(target>nums[right]) return nums.size();while(left<right){int mid = left+(right-left)/2;if(nums[mid]<target) left=mid+1;else right = mid;}return left;}
};6.山脉数组的峰顶索引

山脉数组:从一个值递增到某一个峰值元素然后递减的数组
要求返回山脉数组的峰值元素下标
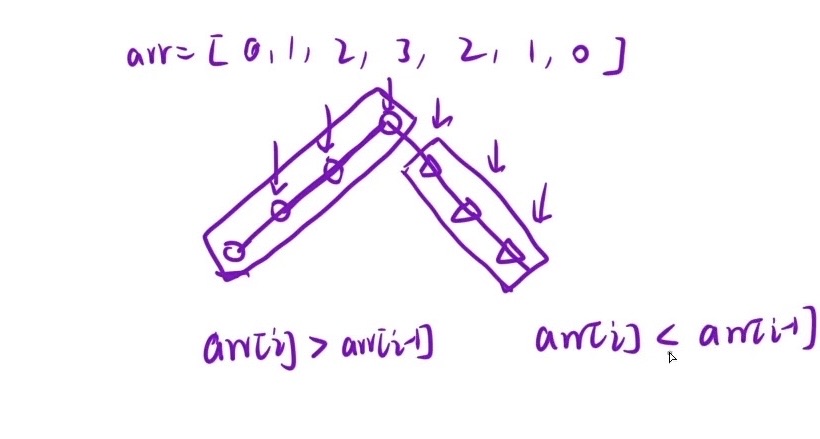
由上图不难发现,左边区间都是后一个元素要大于前一个元素,即 arr[i] > arr[i-1] ;右边区间都是后一个元素要小于前一个元素,即 arr[i] < arr[i-1]
因此山脉数组具有二段性,能够使用二分查找算法
- arr[mid] > arr[mid-1] -> 在左边区间,可能是结果值也可能不是,所以 left = mid
- arr[mid] < arr[mid-1] -> 在右边区间,绝对比结果值要小,所以 right = mid - 1
如果要用寻找区间左端点的方法来解决题目,需要把比较条件换为 arr[mid+1] 与 arr[mid] 的比较
代码:
class Solution {
public:int peakIndexInMountainArray(vector<int>& arr) {int left=0,right=arr.size()-1;while(left<right){int mid = left+(right-left+1)/2;if(arr[mid]<arr[mid-1]) right = mid-1;else if(arr[mid]>arr[mid-1]) left = mid;}return left;}
};7.寻找峰值

峰值元素:比左边相邻元素和右边相邻元素都大的元素
一个数组中有多个峰值元素,找出其中一个的下标返回;并且num[-1] = nums[n] = -∞,相邻两元素不可能相等
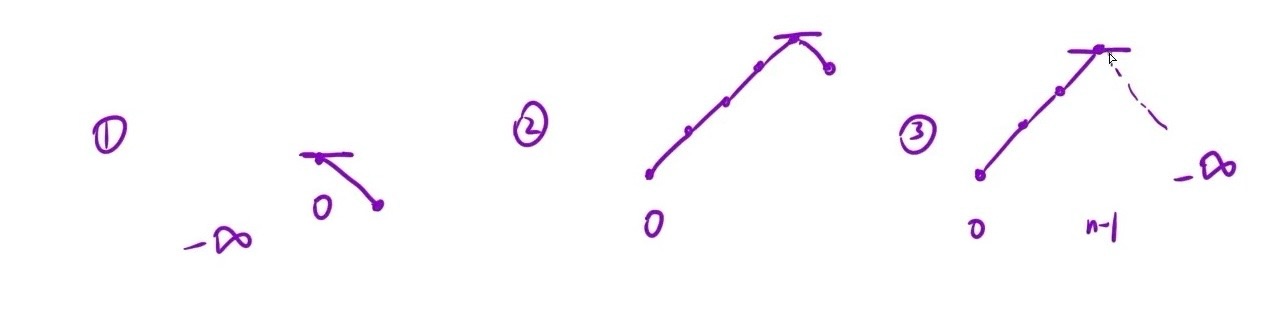
1.暴力解法:
从第一个位置开始,一直向后走,分以下3种情况讨论即可
- 数组元素单调递减,那么数组首元素为峰值
- 数组元素时增时减,在其中必然有一个元素比前后两个相邻位置元素都大
- 数组元素单调递增,那么数组最后一个元素为峰值
当为情况3时,是最坏情况,需要执行n次操作,即时间复杂度为O(N)
2.二分查找
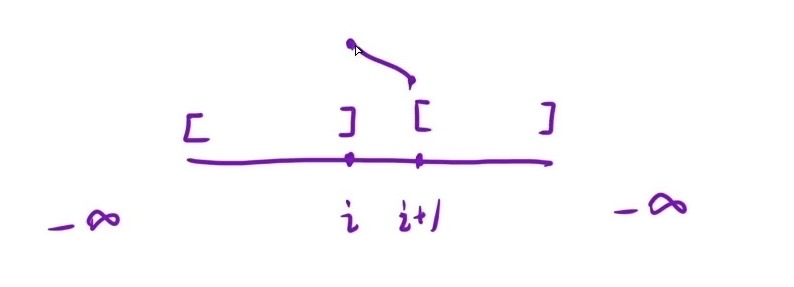
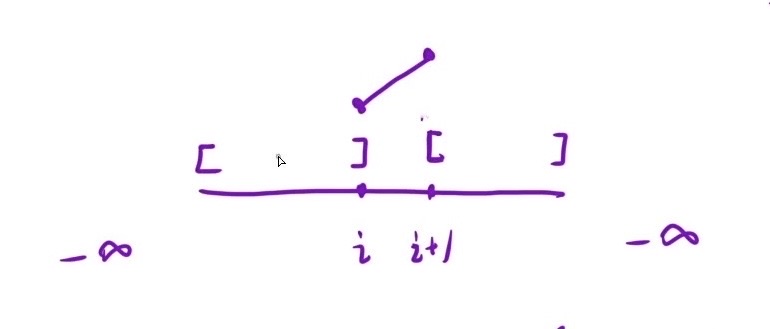
通过下面两张图不难看出一个二段性规律,即:
- 当 i 位置的元素要比后面一个元素大,因为具有增长的趋势才能够由增变为减,所以此时 i 所在的左边区间必然有一个或一个以上的峰值,可能是其本身也可能是前面出现的某一个值,恰好对应了暴力解法的情况1、情况2;同时右边那个区间,由于可以单调递减到数组最后一个元素,所以不一定存在峰值
- 与上同理,当 i 位置的元素要比后面一个元素小,此时 i + 1 位置处的元素具有增长趋势,右边区间肯定有一个峰值,左边区间不一定
nums[mid] > nums[mid+1],right = mid;nums[mid] < nums[mid+1],left = mid + 1
代码:
class Solution {
public:int findPeakElement(vector<int>& nums) {int left = 0,right = nums.size() - 1;while(left<right){int mid = left+(right-left)/2;if(nums[mid]>nums[mid+1]) right = mid;else left = mid + 1;}return left;}
};8.寻找旋转排序数组中的最小值

一个升序排序数组,经过向后旋转(最后一个元素变为首元素,其他元素向后移位1个下标)得到了nums数组,现要求通过nums数组直接找到数组最小元素,所有元素为互不相同的整数
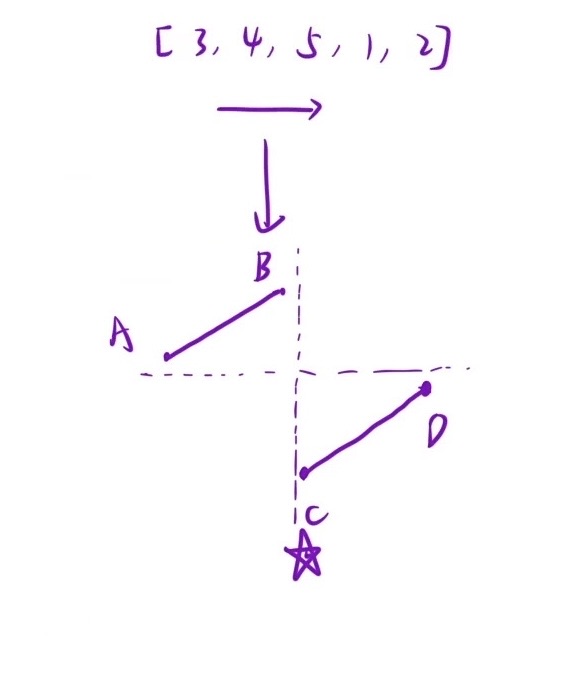
如上图所示,我们可以把一整个nums数组抽象成两段;A -> B 段元素全都要比 D 点(nums数组中最后一个元素)大,C -> D 段元素全都要比 D 点小或恰好相等
因此满足二段性,可以使用二分查找来解决这道题,最终 C 点即为数组最小值
- nums[mid] > nums[n-1] -> 落在了左边区间,结果值肯定在其右边区间里 -> left = mid + 1
- nums[mid] <= nums[n-1] -> 落在右边区间,结果值可能为其本身也可能在其左边 -> right = mid
代码:
class Solution {
public:int findMin(vector<int>& nums) {int n = nums.size();int left = 0,right = n-1;while(left<right){int mid = left+(right-left)/2;if(nums[mid]<=nums[n-1]) right = mid;else left = mid + 1;}return nums[left];}
};代码易错点:要返回的是最小元素,而不是最小元素所在的下标!!!
9.丢失的数字

一个数组中有 n - 1 个元素,元素范围为 [0,n] 的整数,每个整数只出现一次,要求找到 [0,n] 范围内一次也没出现过的整数
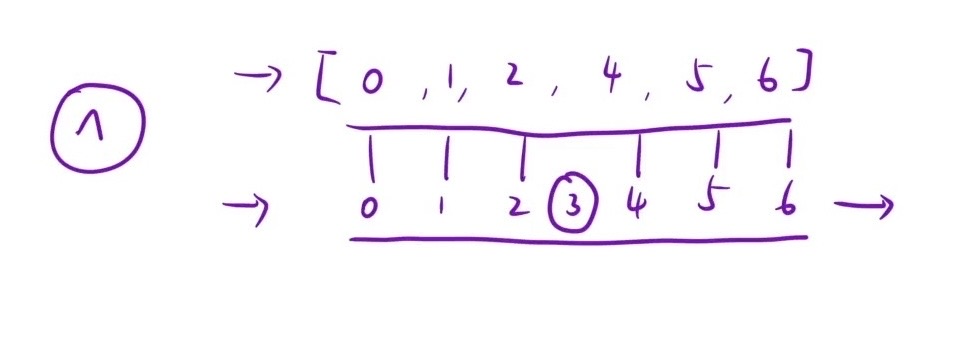
思路1:等差数列求和
通过等差数列求和公式把[0,n]所有数据相和,然后与nums数组中所有元素相减,相减后剩下的值即为丢失的数字
代码:
class Solution {
public:int missingNumber(vector<int>& nums) {int n = nums.size();int Sn = ((n+1) * n) / 2;for(auto i:nums) Sn-=i;return Sn;}
};思路2:二分查找
先对数组进行排序,排序完毕后通过数组下标来和元素值进行比较;如下图所示,有一段区间值与数组下标相等,有一段区间值比数组下标要大,二分查找解决二段性问题
index == value -> 结果在其右边的区间 -> left = mid + 1
index < value -> 结果可能在其左边的区间,也可能为其本身 -> right = mid
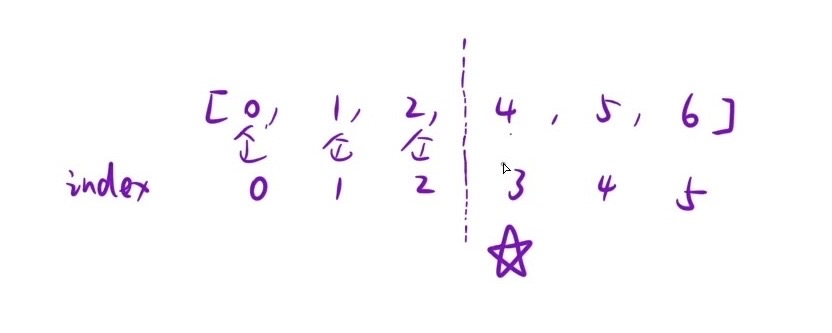
需要注意的是例2的情况,丢失的数字无法通过下标来表示,因为数组下标最大就到1但需要返回的却是2,因此需要特判
return left == nums[left] ? nums.size() : left;
代码:
class Solution {
public:int missingNumber(vector<int>& nums) {sort(nums.begin(),nums.end());int left=0,right=nums.size()-1;while(left<right){int mid = left + (right - left) / 2;if(mid == nums[mid]) left = mid + 1;else right = mid;}return left == nums[left] ? nums.size() : left;}
};