单遍聚类:实时数据流聚类解决方案
文章目录
- 一、核心思想
- 二、算法流程
- 三、示例
- 四、优缺点
- 优点
- 缺点
- 解决方案
- 五、参数调优
- 六、与其他算法对比
- 七、应用场景
- 八、扩展与变体
- 九、总结
单遍聚类是一种计算高效的聚类算法,适合处理大规模数据集或数据流,它的核心特点是只需对数据进行一次扫描。
一、核心思想
单遍聚类读取数据的过程中,动态地创建和更新聚类,它不需要预先知道聚类数量或进行多次迭代。它会逐个检查数据点,并根据某种相似性度量(通常是距离)决定是将该点归入已有的聚类中,还是以其为中心创建一个新的聚类。
二、算法流程
- 初始化
设定两个关键参数:阈值和半径,并创建一个空的聚类列表。
- 阈值:一个距离阈值,用于判断一个点是否属于某个聚类。
- 半径:影响范围,通常与阈值相关,可以理解为聚类的“势力范围”。
-
读取数据点
从数据集或数据流中读取下一个数据点P。 -
寻找最近的聚类
计算点P到所有已有聚类中心(或代表点)的距离。
找到距离P最近的那个聚类C,并记该距离为D_min。 -
决策
- 如果 (D_min ≤ 阈值):
- 则认为点P属于聚类 C;
- 更新聚类C,将点P并入聚类C,
- 并立即重新计算聚类 C的新中心。
- 否则 (D_min > 阈值):
- 认为点P不属于任何现有聚类;
- 以点P为中心,创建一个新的聚类;
- 并将这个新聚类加入到聚类列表中。
- 循环
重复2-4,直到所有的数点都被处理完毕。
三、示例
import numpy as np
import matplotlib.pyplot as pltclass SinglePassClustering:def __init__(self, threshold):self.threshold = threshold # 距离阈值self.clusters = [] # 存储每个聚类的中心点self.points_in_clusters = [] # 存储每个聚类中包含的点def euclidean_distance(self, p1, p2):return np.sqrt(np.sum((np.array(p1) - np.array(p2)) ** 2))def fit(self, points):for point in points:if not self.clusters:# 第一个点直接成为一个聚类self.clusters.append(point)self.points_in_clusters.append([point])else:# 计算到所有聚类中心的距离distances = [self.euclidean_distance(point, center) for center in self.clusters]min_distance = min(distances)closest_cluster_idx = np.argmin(distances)if min_distance <= self.threshold:# 归入最近聚类self.points_in_clusters[closest_cluster_idx].append(point)# 更新聚类中心:取均值cluster_points = self.points_in_clusters[closest_cluster_idx]self.clusters[closest_cluster_idx] = np.mean(cluster_points, axis=0)else:# 创建新聚类self.clusters.append(point)self.points_in_clusters.append([point])def plot_clusters(self):colors = plt.cm.get_cmap('tab10', len(self.clusters))for i, points in enumerate(self.points_in_clusters):pts = np.array(points)plt.scatter(pts[:, 0], pts[:, 1], color=colors(i), label=f'Cluster {i+1}')centers = np.array(self.clusters)plt.scatter(centers[:, 0], centers[:, 1], color='black', marker='x', s=100, linewidths=2, label='Centers')plt.legend()plt.title('Single-Pass Clustering')plt.show()# 示例使用
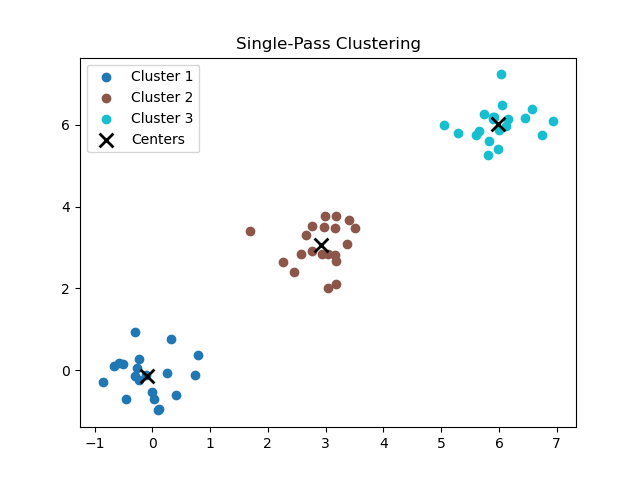
if __name__ == "__main__":# 生成一些示例数据np.random.seed(42)data1 = np.random.normal(0, 0.5, (20, 2))data2 = np.random.normal(3, 0.5, (20, 2))data3 = np.random.normal(6, 0.5, (20, 2))points = np.vstack([data1, data2, data3])# 创建聚类器并拟合spc = SinglePassClustering(threshold=2.0)spc.fit(points)# 输出聚类结果print(f"生成聚类数量: {len(spc.clusters)}")for i, center in enumerate(spc.clusters):print(f"聚类 {i+1} 中心: {center}")# 可视化聚类结果spc.plot_clusters()
四、优缺点
优点
- 效率高:只需扫描一次数据,时间复杂度近似于 O(n),其中n是数据点的数量。这对于海量数据或实时数据流至关重要。
- 无需指定聚类数量:聚类数量是在过程中自动确定的。
- 实现简单:算法简单,易于编程实现。
缺点
- 输入顺序敏感:这是最大的缺点。数据点的输入顺序会显著影响最终的聚类结果。先来的点会优先形成聚类中心,后来的点则依赖于已有的中心进行判断。这可能导致不是最离线的聚类划分。
- 依赖阈值参数:阈值的选择非常关键,直接影响聚类的大小和数量。
- 阈值过大:会导致许多不相似的点被归入同一个聚类,甚至所有点都被聚为一类。
- 阈值过小:会导致产生大量细小的、分散的聚类,甚至每个点都自成一类。
- 难以发现任意形状的聚类:由于通常使用欧氏距离等度量,并以中心点代表整个聚类,它更倾向于发现球形或凸形的聚类,难以处理环形、流形等复杂形状。
- 对噪声和离群点敏感:一个离群点也会被当作一个新聚类的种子,从而产生没有意义的微小聚类。
解决方案
为克服单遍聚类对球形聚类的偏好,可采用以下改进策略:
- 多代表点机制:用多个中心点代替单一中心表征聚类,更好地捕捉复杂形状
- 边界点表征:基于边界点定义聚类范围,增强对非凸形状的识别能力
- 多阈值分层:采用多级距离阈值,构建层次化聚类结构
- 图连通性分析:通过点间连通关系判断聚类归属,突破距离限制
这些方法通过改进聚类的表征方式和相似性判断逻辑,在保持算法高效性的同时,能够提升了对任意形状聚类的发现能力。
五、参数调优
阈值选择:建议在数据子集上尝试多个阈值,观察聚类数量与质量的变化。
最小聚类大小:可设置一个最小点数,避免噪声点形成无效聚类。
距离度量:根据数据特性选择欧氏距离、余弦距离等。
六、与其他算法对比
| 特性 | 单遍聚类 | K-Means | DBSCAN |
|---|---|---|---|
| 扫描次数 | 单次 | 多次迭代 | 单次(但需要邻域查询) |
| 聚类形状 | 球形 | 球形 | 任意形状 |
| 是否需要指定k | 否 | 是 | 否 |
| 处理噪声 | 差 | 差 | 优 |
| 顺序敏感性 | 高 | 低(但初始中心敏感) | 低 |
| 效率 | 非常高 (O(n)) | 一般 (O(n * k * i)) | 依赖于数据结构 (O(n log n)) |
七、应用场景
数据流挖掘:例如,实时监控网络流量数据,对其进行实时分类和异常检测。
大规模数据的初步分析:作数据探索的第一步,快速了解数据大致分布情况,为后续更精细的分析提供参考。
计算资源有限的环境:如在嵌入式设备或边缘计算中,需要轻量级的机器学习算法。
八、扩展与变体
单遍聚类+滑动窗口:适用于时间序列数据,只保留最近一段时间内的聚类。
单遍聚类+采样:先对大数据集采样,再用单遍聚类快速建模。
单遍聚类+集成:多次随机排序数据运行,集成多个聚类结果。
九、总结
单遍聚类是一种简单、快速、增量式的聚类算法。它牺牲了对聚类质量的保证(受顺序影响大)和发现复杂结构的能力,换来了无与伦比的处理速度。它不是一个“强大”的聚类算法,但在特定的、对效率要求极高的场景下,它是一个非常实用和有效的工具。
