LeetCode 124. 二叉树中的最大路径和(困难)
题目描述
二叉树中的 路径 被定义为一条节点序列,序列中每对相邻节点之间都存在一条边。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点,且不一定经过根节点。
路径和 是路径中各节点值的总和。
给你一个二叉树的根节点 root ,返回其 最大路径和 。
示例
示例 1:
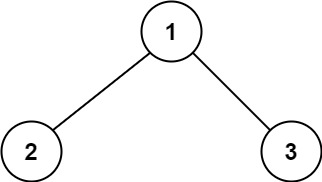
输入:root = [1,2,3] 输出:6 解释:最优路径是 2 -> 1 -> 3 ,路径和为 2 + 1 + 3 = 6
示例 2:
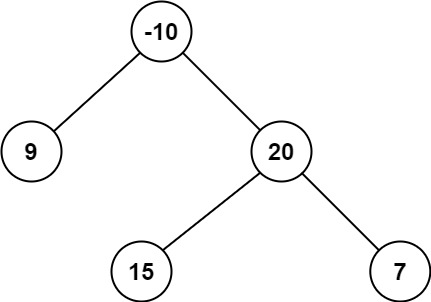
输入:root = [-10,9,20,null,null,15,7] 输出:42 解释:最优路径是 15 -> 20 -> 7 ,路径和为 15 + 20 + 7 = 42
解法
1.递归
解题思路
二叉树 abc,a 是根结点(递归中的 root),bc 是左右子结点(代表其递归后的最优解)。
最大的路径,可能的路径情况:

- b + a + c。
- b + a + a 的父结点。
- a + c + a 的父结点。
其中情况 1,表示如果不联络父结点的情况,或本身是根结点的情况。这种情况是没法递归的,但是结果有可能是全局最大路径和。情况 2 和 3,递归时计算 a+b 和 a+c,选择一个更优的方案返回,也就是上面说的递归后的最优解啦。
另外结点有可能是负值,最大和肯定就要想办法舍弃负值(max(0,x))。但是上面 3 种情况,无论哪种,a 作为联络点,都不能够舍弃。
代码中使用 val 来记录全局最大路径和,ret 是情况 2 和 3,lmr 是情况 1。所要做的就是递归,递归时记录好全局最大和,返回联络最大和。
联络的意思就是例子中,b和c是没有直接连接的,通过a点,这3个点连在一起,这时a点就把b和c联络在一起,但是通过a联络bc就无法再向a的上层连线了。
class Solution {
public:int maxPathSum(TreeNode* root, int &val){if (root == nullptr) return 0;int left = maxPathSum(root->left, val);int right = maxPathSum(root->right, val);int lmr = root->val + max(0, left) + max(0, right);int ret = root->val + max(0, max(left, right));val = max(val, max(lmr, ret));return ret;}int maxPathSum(TreeNode* root) {int val = INT_MIN;maxPathSum(root, val);return val;}
};