深度学习(十四):正则化与L2正则化
什么是正则化?
在深度学习中,正则化是一系列旨在减少模型泛化误差而非训练误差的技术。其核心目的是防止模型在训练数据上过拟合(Overfitting),从而提高模型在未见过的新数据上的表现能力。过拟合通常表现为模型在训练集上表现极佳,但在验证集或测试集上表现较差。
模型过拟合的原因往往是其复杂度过高,拥有过多的自由度,能够“记住”训练集中的噪声和随机波动,而不是学习到数据背后的普遍规律。正则化通过约束模型的复杂度来对抗这种现象。
正则化的目标与作用
- 防止过拟合: 这是正则化最主要的目的。通过限制模型参数的可能取值范围或值的幅度,减少模型对训练数据细节的依赖。
- 提高泛化能力: 使模型学习到的特征更具有普遍性,从而在未知数据上也能保持较高的准确性。
- 简化模型: 促使模型选择更简单的解释,这符合奥卡姆剃刀原则(Occam’s Razor):在同样能解释数据的情况下,选择最简单的模型。
L2正则化:原理、推导与特性
L2正则化(L2 Regularization),又称岭回归(Ridge Regression),是深度学习中最常用且最有效的正则化方法之一。
L2正则化的数学原理
L2正则化通过在模型的损失函数(Loss Function)**中添加一个与**模型权重的平方和成正比的项来实现。
原始的损失函数(例如:交叉熵损失 J0):
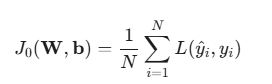
加入L2正则化项后的总损失函数 J(W,b):
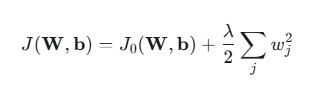
其中:
- J0 是模型的原始损失函数(如均方误差、交叉熵)。
- W={wj} 是模型中的所有权重参数(通常不对偏置项 b 进行正则化)。
- wj 是模型中的第 j 个权重。
- λ(Lambda)是正则化系数(或正则化率),它是一个超参数,用于控制正则化项对总损失的贡献程度。λ 越大,对权重的惩罚越大。
- ∑jwj2 即为权重向量的 L2 范数(Euclidean norm)的平方,记作 ∣∣W∣∣22。
L2正则化如何防止过拟合?
L2正则化的作用在于惩罚较大的权重值。为了最小化总损失 J,模型在优化过程中不仅要最小化原始损失 J0,还要设法使权重 W 接近于零。
- 平滑模型: L2正则化倾向于使模型中所有的权重都比较小且接近于零,但不会使它们精确地变为零。较小的权重意味着输入数据的微小变化只会导致输出的较小变化,使模型对输入的扰动不那么敏感,从而更平滑、更简单。
- 梯度更新与权重衰减(Weight Decay): 在进行梯度下降时,权重的更新公式会受到正则化项的影响。以最简单的线性模型为例,对 L2 正则化项求导得:
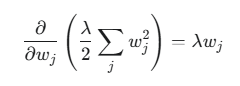
因此,更新规则变为:
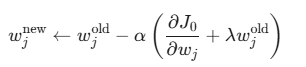
其中 α 是学习率。上式可重写为:
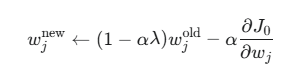
可以看到,每进行一次梯度更新,权重 wjold 都会先乘上一个小于 1 的因子 (1−αλ) 进行衰减,然后再减去原始损失的梯度。这就是 L2 正则化也被称为权重衰减的原因。
L1正则化与L2正则化的比较
L2正则化是**“正则化”**这一大类技术中的一种。与L2正则化并列的另一个重要方法是 L1正则化(L1 Regularization),又称 Lasso 回归。
| 特征 | L2 正则化(Ridge/权重衰减) | L1 正则化(Lasso) |
|---|---|---|
| 正则化项 | 权重的平方和($ | |
| 损失函数 | $J_0 + \frac{\lambda}{2} | |
| 对权重的影响 | 使所有权重都趋向于零,但不会精确为零。 | 使许多权重精确地变为零。 |
| 稀疏性 | 不具备稀疏性。所有特征都保留,但系数很小。 | 具备稀疏性。可以用于特征选择(Feature Selection)。 |
| 可微性 | 完全可微,优化计算效率高。 | 在零点不可微,优化过程略复杂。 |
| 几何解释 | 损失函数等高线与 L2 约束区域(圆/球体)的交点。 | 损失函数等高线与 L1 约束区域(菱形/立方体)的交点。 |
**稀疏性(Sparsity)**是L1正则化与L2正则化最核心的区别。L1正则化会把不重要的特征对应的权重直接置为零,因此可以实现自动的特征选择;而L2正则化则保留所有特征,但使它们的权重都很小。在特征数量非常庞大且需要筛选时,L1正则化可能更合适。在大多数深度学习场景中,L2正则化因其平滑且计算友好的特性而更为常用。
L2正则化的应用优势
- 计算高效: L2正则化项是可微的,这使其能顺利集成到基于梯度下降的优化算法中,计算简单且高效。
- 模型稳定: 通过缩小权重,L2正则化能增强模型的抗扰动能力,使模型的预测结果对输入数据的微小变化更稳定。
- 贝叶斯解释: 从贝叶斯统计的角度看,L2正则化等价于假设模型参数 wj 服从零均值的高斯先验分布(Normal/Gaussian Prior)。这种先验信息鼓励参数取接近于零的值。
- 易于调参: 只需要调整一个超参数 λ。通常通过在验证集上进行网格搜索或随机搜索来找到最优的 λ 值。
总结
正则化是确保深度学习模型从“记住”训练数据到“理解”普遍规律的关键桥梁。L2正则化作为其中最基础和重要的方法之一,通过惩罚权重的大小,有效地降低了模型的复杂度,提高了模型的泛化能力。它通过在每次参数更新时引入权重衰减,促使模型选择更小的权重值,从而获得更平滑、更稳定的决策边界。
在实践中,除了L2/L1正则化外,深度学习中还有其他重要的正则化技术,例如:
- Dropout: 在训练过程中随机地“关闭”一部分神经元,防止神经元之间的共适应。
- 数据增强(Data Augmentation): 通过对训练数据进行随机变换(如旋转、裁剪、翻转),增加训练样本的多样性。
经元,防止神经元之间的共适应。 - 数据增强(Data Augmentation): 通过对训练数据进行随机变换(如旋转、裁剪、翻转),增加训练样本的多样性。
- 早停法(Early Stopping): 在模型在验证集上的性能开始恶化时就停止训练。
