深度学习周报(9.29~10.5)
目录
摘要
Abstract
1 QKV推导
2 量子传输
3 量子计算基本代码
4 总结
摘要
本周首先了解了QKV的具体推导过程;其次学习了量子传输的相关知识,主要包括关键点、过程与优缺等,同时对共享纠缠对的方法做了补充;最后入门了量子计算的基础代码,了解了其运行过程与一些常用的函数模块,如QuantumCircuit和BasicSimulator等。
Abstract
This week, I first learned the specific derivation process of QKV; secondly, I studied quantum teleportation, mainly including its key points, procedures, advantages and disadvantages, and also supplemented the method of sharing entangled pairs; finally, I got started with the basic code of quantum computing, understanding its execution process and some commonly used function modules, such as QuantumCircuit and BasicSimulator.
1 QKV推导
上周学习了注意力机制的大体内容,这周具体了解一下其中qkv的推导过程。
以自注意力机制为例,假设我们有一个输入序列,其嵌入表示为矩阵 ,其中
是序列长度(比如句子中的词数),
是每个词的嵌入维度,即将一个离散的词汇映射到一个连续的、固定长度的数值向量时,这个向量的长度。
由于Q、K、V分别代表着不同的信息,所以我们通过三个不同的可学习权重矩阵对输入 进行线性变换,得到 Query、Key 和 Value 矩阵,公式分别如下:
其中:,
,
是可学习的权重矩阵,对于 Q 和 K,维度通常为
;对于V, 维度则通常为
。由此,Q, K, V 的维度分别为
,
,
。在标准的缩放点积注意力中,通常
=
=
,h 是注意力头数。
通过分离这三个角色,模型就可以更灵活地学习查询、匹配和信息提取的策略。如果 Q=K=V=X,模型的表达能力会受限。
例子(以“I need water”为例,假设词嵌入维度为 4, =
= 2,故三个权重矩阵维度为
,Query、Key 和 Value 矩阵维度为
):
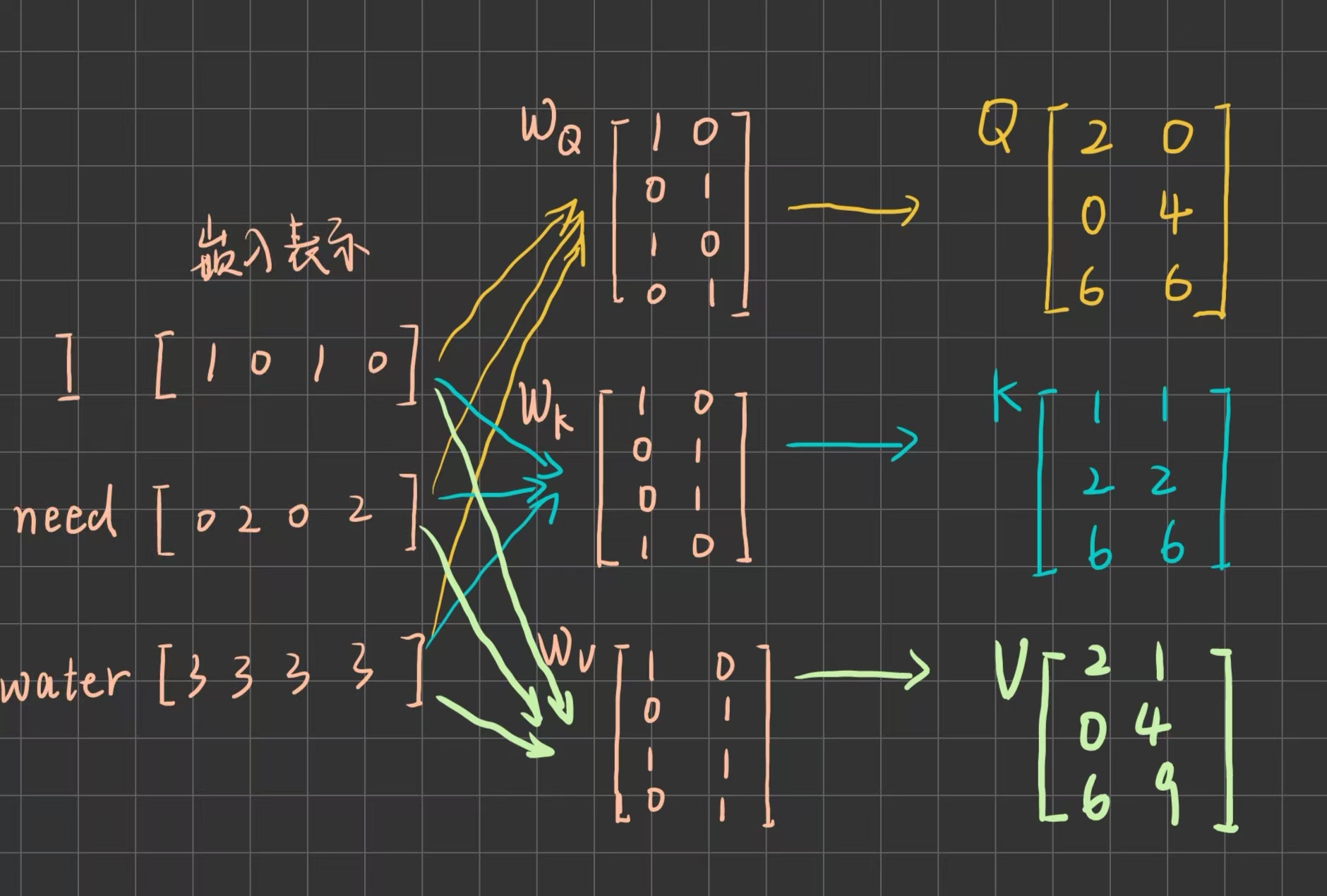
假设想用自注意力机制来理解 need 这个词,计算如下:

softmax的计算公式为:
其中 是输入向量中的第 i 个元素;
表示对当前元素进行指数运算,从而放大较大的值,抑制较小的值。
是对整个输入向量中所有元素的指数值进行求和。上述缩放分数向量,经过softmax 分别是两位数除以七位数,三位数除以七位数和七位数除以七位数,故可近似为上图结果。

可以发现,need 的注意力输出完全来自于 water 的 Value 向量,明显不合理,这是因为这只是一个以供学习的例子,权重矩阵是任意设定的,并不一定合理,在实际的应用中需要通过大量的数据训练得到能够合理地反映语义相似性的权重。
2 量子传输
“量子传输”通常指的是量子隐形传态(Quantum Teleportation),即是一种利用预先共享的量子纠缠和经典通信,将一个未知的量子态从一个位置精确地传输到另一个遥远位置的技术。
它的关键点有三。第一,它传输的是信息或状态,而不是物质本身;第二,它依赖经典信道,由于经典信息的传递速度不能超过光速,所以并不违反相对论,特别是爱因斯坦的狭义相对论中“信息不能超光速传播”这一基本原则;第三,它遵循上周提到的量子不可克隆定理(No-Cloning Theorem),在传输完成后,原始的量子态消失,只在目标位置重建。
量子隐形传态与超密编码互为“对偶”,超密编码用1个量子比特和1个纠缠对传输2个经典比特,而它用2个经典比特和1个纠缠对传输1个未知量子比特,此两者共同揭示了量子资源与经典资源之间的等价转换关系。它们都称发送方为Alice,接收方为Bob。
假设Alice想要把一个未知的量子态 (记为粒子1)传送给Bob,它的步骤大致如下:
首先,假设Alice和Bob(即发送方与接收方)事先共享一对处于 的纠缠对,Alice持有第一个粒子(记为qubit A),Bob持有第二个粒子(记为qubit B);
p.s. 这一步与超密编码一样,可以进行适当扩充其共享过程,如下:
一个第三方(或Alice、Bob)制备一对处于贝尔态的纠缠粒子,如:,将其中一个粒子(记为qubit B)发送给Bob,另一个(qubit A)则留在Alice处,此时,Alice和Bob各自持有一个纠缠粒子,共享一对处于
的纠缠粒子。这儿的发送不同于量子隐形传态,因为并未事先共享纠缠对,主要采用光纤传输、自由空间传输还有量子中继器等方式进行,发送的也是量子比特的状态。
其次,Alice对粒子1和 qubit A 进行一次联合贝尔态测量(Bell-State Measurement, BSM),这个测量会将这两个粒子投影到四个可能的贝尔态( 、
、
、
,与下文经典信息相对应,对应关系可能因文献而异)之一上,同时摧毁原始的量子态;
然后,Alice将2比特的经典信息(00, 01, 10, 或 11)通过经典信道发送给Bob;
最后,Bob收到经典信息后,根据这2比特的信息,对自己的纠缠粒子(粒子2)执行相应的量子门操作(如I, X, Z, 或 ZX)。经过正确的操作后,Bob的粒子就会变成与Alice想要传输的未知量子态完全相同的量子态。
量子隐形传态能够实现未知量子态的远程传输,在遵循量子不可克隆定理的前提下,可以将一个完全未知的量子态从一个地点精确地传输到另一个地点;而且这种传输是不依赖物理载体的直接传输,特别适用于脆弱量子态(如光子偏振、原子能级)的长距离传输,避免在信道中退相干或丢失;它在突破经典通信限制的同时,安全性和实验可行性都比较高(中国“墨子号”卫星实现了1200公里的星地量子隐形传态,验证了远距离可行性),是构建量子网络、量子中继器和分布式量子计算的核心技术,能够为量子互联网奠定基础。
但是量子隐形传态与超密编码一样,需要预先共享纠缠资源并进行贝尔态测量,前者代表不仅在通信前必须先建立并分发纠缠对,且纠缠态极易受环境干扰(退相干),长距离分发损耗大、效率低;后者效率低,技术难度高(具体在上周有所说明)。其次它需要经典信道发送比特信息来传递量子信息,整体速度受限于光速,但又只能用于发送量子信息,不能发送经典信息。同时,其可扩展性也面临挑战,因为构建大规模量子网络需要大量纠缠源、中继器和节点同步,当前技术距离“全球量子互联网”仍有很长的路要走。
3 量子计算基本代码
量子计算主要利用的是 Qiskit 库,它是目前最流行、生态最完善的开源量子计算框架,提供从电路设计、模拟到在真实IBM量子计算机上运行的完整工具链,且支持多种后端,适用于量子计算入门、教学、研究、算法开发等场景,是许多初学者和研究者的学习量子计算代码的首选。
其安装方式如下:
pip install qiskit下面是创建一个量子比特,将其置于叠加态,并进行测量的代码步骤:
首先,导入必要的模块;
from qiskit import QuantumCircuit, transpile
from qiskit.providers.basic_provider import BasicSimulator
from qiskit.visualization import plot_histogram其中 QuantumCircuit 是 Qiskit 中最核心的类,它代表一个量子电路,可以被想象成一张空白画布,可以在其上创建量子比特和经典比特的寄存器,添加量子门。进行测量打印等操作;transpile 是一个编译优化函数,可以将设计的通用量子电路转换成一个特定量子设备或模拟器能够理解和高效执行的版本;BasicSimulator 是一个运行在经典计算机上的模拟器,用于模拟量子计算机的行为;plot_histogram则主要用于可视化。
其次,创建一个量子电路,该电路包含1个量子比特和1个经典比特,经典比特用于存储测量结果,量子比特自动被隐式地初始化为 ;
qc = QuantumCircuit(1, 1) # (量子比特数量, 经典比特数量)然后,应用一个Hadamard门 (H门),将 变成叠加态
,这在前面的学习也有提到。随后对量子比特进行测量,并将结果存储在第0个经典比特中。
qc.h(0) # 对第0个量子比特应用H门qc.measure(0, 0) # 测量量子比特(想要测量的量子比特索引,存储测量结果的经典比特的索引)进行打印。
print("量子电路:")
print(qc)结果如下:
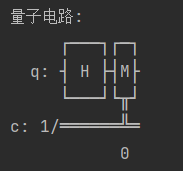
接着,将设计好的电路放到模拟器上运行并获取测量结果;
simulator = BasicSimulator() #创建量子模拟器实例compiled_circuit = transpile(qc, simulator) #将设计的电路优化为适合模拟器的版本job = simulator.run(compiled_circuit, shots=1000) #运行
#Job 对象代表了提交的计算任务,即使计算还没完成,也可以利用它来跟踪状态。
#shots指定了电路完整运行的次数,每次运行都会产生一组经典测量结果。result = job.result() #阻塞调用,会暂停程序,直到模拟器完成所有运行,并将结果打包好,返回一个 Result 对象。counts = result.get_counts(compiled_circuit) #获取测量结果最后,对测量结果进行可视化。
plot_histogram(counts).show()结果如下:
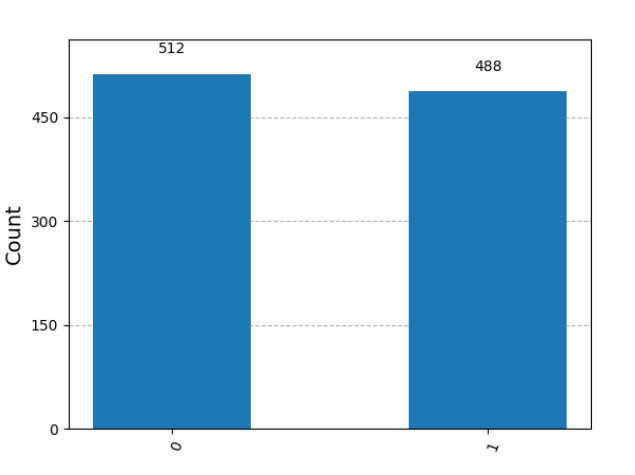
可以发现,在1000次实验中,512次的结果是0,488次为1,这也接近H门创建的叠加态的预期结果(一半为0,一半为1)。
4 总结
本周主要基于上周的学习,对QKV的推导与量子传输进行了了解,同时梳理了前面接触的量子计算入门代码。下周打算学习Transformer中的位置编码与残差连接,并整体复盘其架构,加深理解,量子部分可能开始着手学习Deutsch-Jozsa算法或者simon算法,因为前者在前面的学习中有所提及。
