Kaggle医学影像识别（二）

4 数据导入与医疗图像的数据增强

在完成数据探索、并确定基本的预处理方向之后，我们开始正式对医疗图像（特别地，病理图像）进行预处理。在深度学习当中，我们需要在正式导入图像之前就分割数据集、并设置完整的预处理pipeline，因此我们需要先将训练集测试集分割、再设置好预处理的各项代码、最终将图像导入为PyTorch可以处理的Tensor张量格式。

#PyTorch导入数据的三大基本方法
#torchvision.datasets.SVHN - #Pytorch自带的数据集
#ImageFolder
#CustomData

4.1 定义导入图像的CustomDataset

首先，我们的数据集即不是PyTorch内置数据集、也不符合各种PyTorch类要求的排布规则（例如，ImageFolder要求数据集按标签排列，但我们的数据集是按患者ID排列），因此我们无法使用torchvision.datasets或者ImageFolder来导入数据，必须使用torch.utils.data.Dataset类自主构建导入数据的类CustomDataset。在之前详细讲解Dataset类的用法时我们说明过，在自定义的CustomDataset中，我们需要提供每一个样本（每一张切片）的路径，同时还需要提供每一个样本所对应的标签。为此，我们可以如上一节中所示，统计出每个切片所对应的患者ID、路径、对应标签、切片相对于原始数据的横纵坐标等信息。

• 整理路径与标签信息

#定义目录
PATH = r"E:\02_2022DL\HealthCareProject\IDC_regular_ps50_idx5"#找出目录下所有的患者文件夹
patients = os.listdir(PATH)#将PATH目录下所有的图像统计出来
positive_patches = 0
negative_patches = 0#循环耗时约15s
for patient_id in patients:    #阴性样本的数量class0_path = os.path.join(PATH,patient_id,str(0))class0_patches = os.listdir(class0_path)negative_patches += len(class0_patches)#阳性样本数量class1_path = os.path.join(PATH,patient_id,str(1))class1_patches = os.listdir(class1_path)positive_patches += len(class1_patches)total_patches = positive_patches + negative_patches#新建dataframe，储存患者ID，路径，以及标签
data = pd.DataFrame(index=np.arange(0, total_patches) #对应着每一张具体的图像, columns=["patient_id", "path", "label"])
#开始循环，读出每个切片的信息（循环耗时约2min）
idx = 0
for patient_id in patients:#对每个患者的文件夹，读取其中所有标签下的图像信息for label in [0,1]:class_path = os.path.join(PATH,patient_id,str(label))class_patches = os.listdir(class_path)#对每个标签下的每张图像，记录for patch in class_patches:data.loc[idx,"path"] = os.path.join(class_path,patch)data.loc[idx,"label"] = labeldata.loc[idx,"patient_id"] = patient_ididx += 1

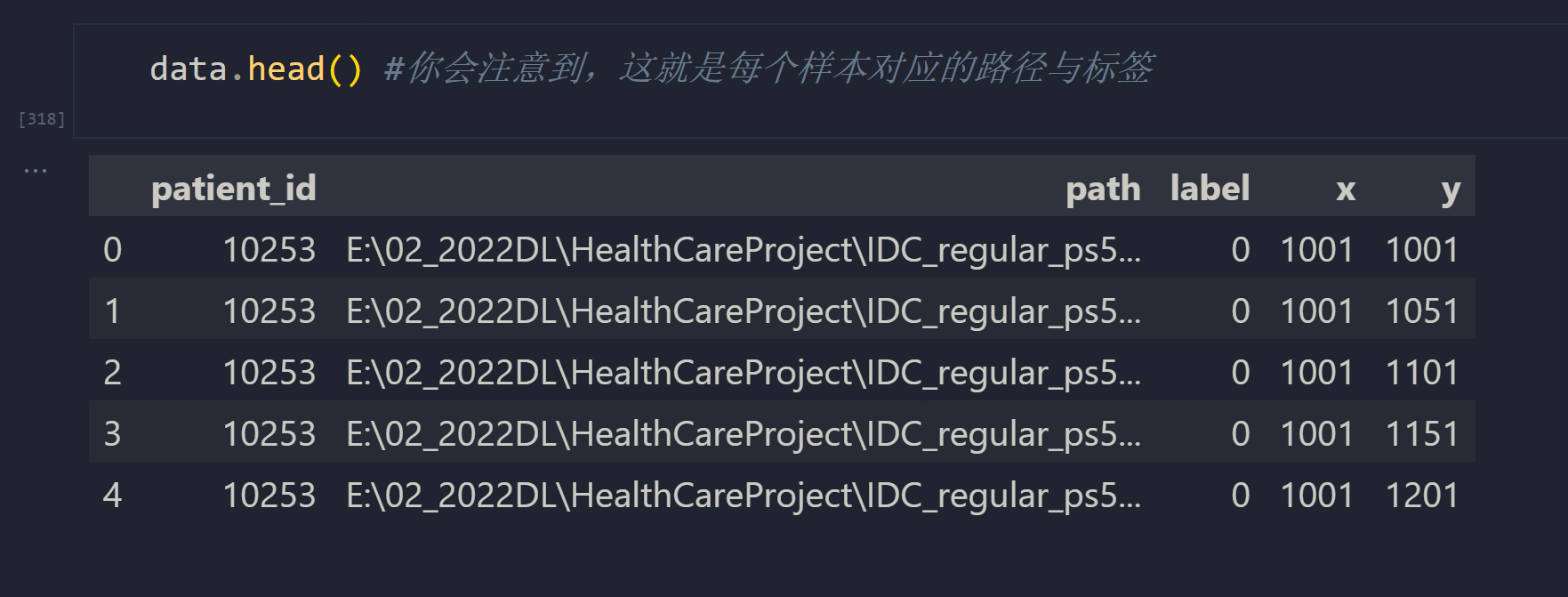
• 分割训练集、测试集、验证集

现在我们已经有了所有样本所对应的路径与标签信息，因此我们只需要在自定义的CustomDataset中按照索引循环具体路径和标签，就可以导入所有的数据了。在PyTorch中，我们可以将全部数据导入之后再使用random_split分割数据集，但考虑到在实际训练过程中，训练集与其他数据集需要使用不同的预处理过程，因此我们往往先分割数据集，再分别导入训练集、测试集和验证集。在这里，我们实际上是要分割即将要被使用的路径和标签（也就是分割建立好的DataFrame），而不是分割了样本本身。

我们可以使用机器学习中常见的train_test_split来帮助我们。在分割时，训练集占比70%，测试集和验证集分别占比15%。如果我们希望模型有更强大的抗过拟合能力，可以缩小训练集的比例、放大测试集和验证集的比例。

from sklearn.model_selection import train_test_splittrain, test_val = train_test_split(data,test_size=0.3,random_state=1412,stratify = data["label"] #新参数，保证标签的分布一致)
test, val = train_test_split(test_val,test_size=0.5,random_state=1412,stratify = test_val["label"])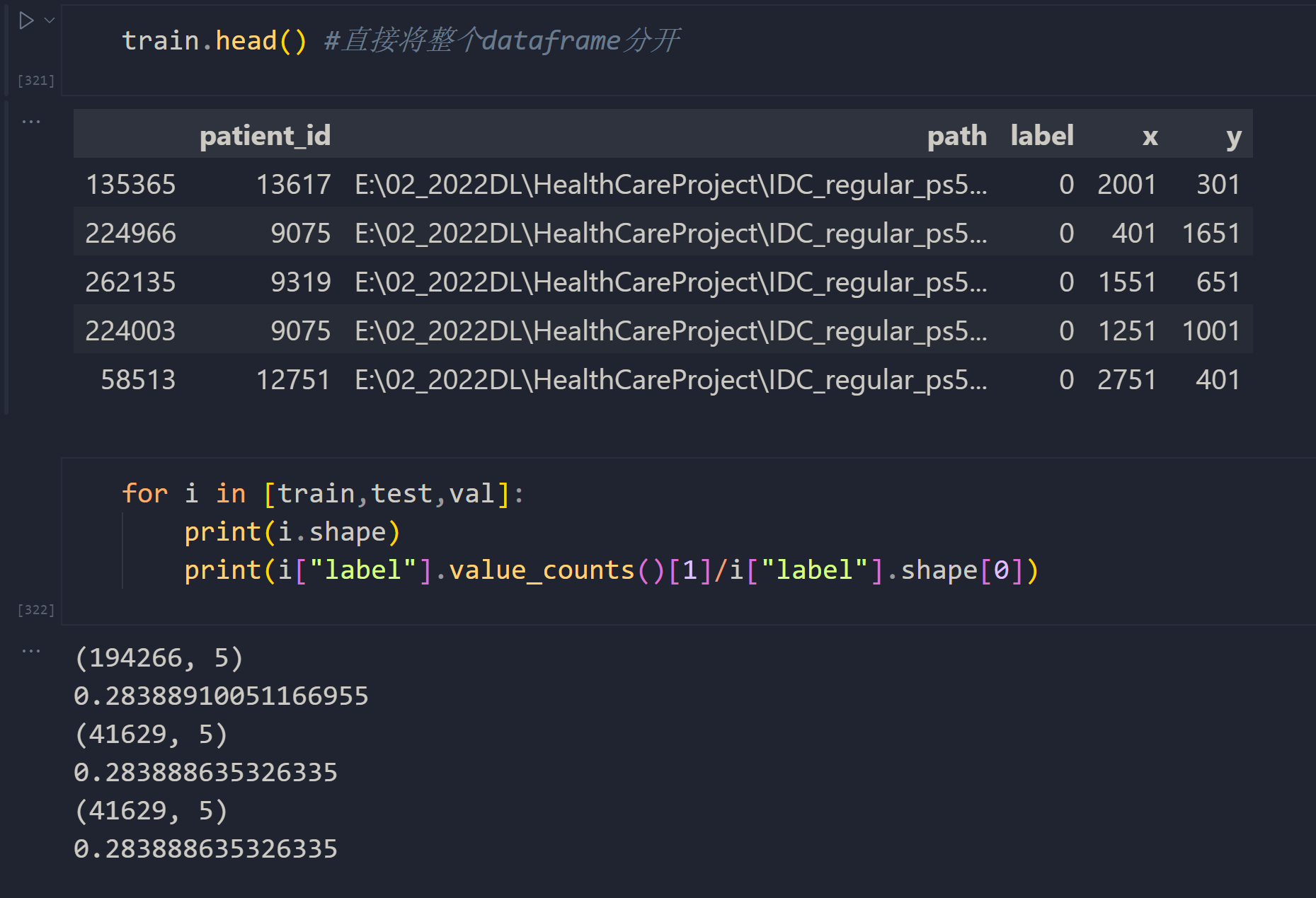

• 定义CustomDataset，导入数据
  现在我们可以来导入数据集了。

from torch.utils.data import Dataset
from skimage import ioclass CustomDataset(Dataset):"""自定义数据集，借助整理好的dataframe读取IDC医疗病理图像数据集的标签和图像图像格式为png"""def __init__(self, df, transform=None):"""参数说明：df：整理好的dataframe，包含全部图像的标签和具体到.png的目录trasnform：选填，需要对样本进行的预处理。"""super().__init__()self.path_label = dfself.transform = transformdef __len__(self):#展示数据中一共有多少个样本return self.path_label.shape[0]def __info__(self):print("IDC data")print("\t Number of Samples: {}".format(self.path_label.shape[0]))print("\t Number of patients: {}".format(len(self.path_label["patient_id"].unique())))def __getitem__(self, idx):#确保idx不是一个tensorif torch.is_tensor(idx):idx = idx.tolist()#图像目录与标签，由于存在df因此这一步变得非常简单patient_id = self.path_label["patient_id"].values[idx]image_path = self.path_label["path"].values[idx]image = io.imread(image_path)label = self.path_label["label"].values[idx]if self.transform:#image = Image.fromarray(io.imread(image_path))image = self.transform(image)sample = {"patch":image,"label":label,"patient":patient_id}return sample

4.2 病理图像数据增强的两大方向

现在定义好了导入数据的CustomDataset，我们可以开始对数据进行预处理和数据增强了。在之前讲解数据增强时，我们曾列举过众多通过PyTorch可以实现的基本增强方式，如旋转、拉伸、色调变化等等，这些增强方式足以应对字母、数字、小型图像识别等场景，但难以在更复杂的数据集上表现优异。

在计算机视觉领域，不同类型的图像需要使用不同的预处理/增强方式，这主要是因为不同图像成像过程存在的干扰因素是大不相同的。例如，之前讲解的对高像素图像进行分片就是医疗、遥感领域特有的预处理方式，而医疗数据当中，病理图像、超声图像和核磁图像又需要完全不同的处理方式。通常来说，对一类图像最有效的数据增强方法必须经过实验得出，因此研究者们孜孜不倦地尝试、探索，并最终将有效的方法总结到论文当中。也因此，在实践深度学习项目之前我们总是希望能够通读这一领域的文献。

幸运的是，医疗领域、特别是病理图像的图像领域有大量文献可以查询，因此从2014年至今出现了大量精彩纷呈的病理图像增强手段，我在这里为大家抛砖引玉，简述一二。

首先，病理图像是搭载标本的整体载玻片扫描而得，基于最基础的初高中生化知识，相信大家能够理解载玻片上的组织需要经过染色后才能够放到显微镜下进行观察。最经济实惠的染色方法是H&E染色，其中H是苏木素（haematoxylin，可以将细胞核染色），E是伊红（eosin，可以将细胞液染色），因此病理图像、组织图像往往呈现红色。我们在进行基础数据探索时便发现，恶性病灶的颜色往往比良性病灶颜色更深，因此色彩的差异可能是神经网络在训练过程中需要学习的一大关键点。然而，在病理图像识别应用中，研究者总是面临的一大挑战是：如何排除不同实验室、不同专业人员、不同批次染色剂、不同扫描仪器、不同玻片原材料、不同组织对颜色的响应程度等等因素而引起的颜色差异，而实现正确的识别。

（图）不同扫描仪下的病理图像

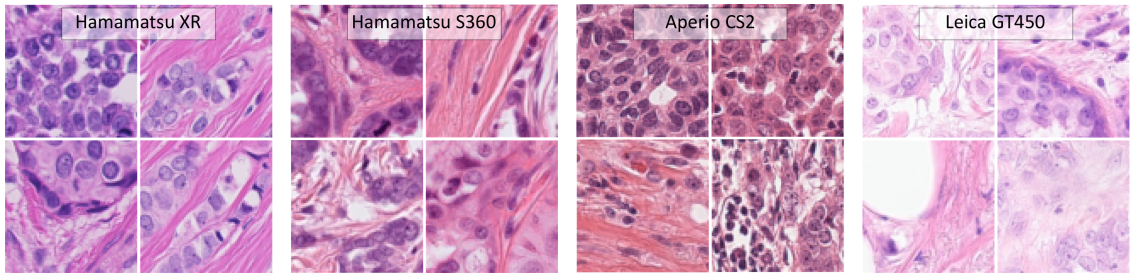
很显然，由于染色、扫描等操作的影响，在一批载玻片上训练的模型在下一批载玻片上预测时就可能失败，这意味着模型的泛化能力严重不足。在实践中，这可能意味着辛苦开发的模型在落地应用时错漏百出，也可能意味着不同医疗机构、不同研究机构之间无法使用相同的模型。

因此，病理图像的预处理/增强一般只有一种目标：排除染色操作干扰，提升模型的泛化能力。在这一目标下，我们不难想到一个解决方案：如果色彩是干扰项，为何不将所有的图像转化为灰度图像呢？早期研究时，的确有许多论文这样操作，但结果不尽如人意。根据计算机视觉开篇时所呈现的色彩基本原理，色彩的深浅本质就是明度，灰度图像也有明度差异。更何况，正是因为不染色状态下的组织无法被观察，才需要对标本进行染色。如果将彩色图像的丰富信息删除，那模型的识别能力会大打折扣，因此将图像变灰没有成为主流手段。然而，后来人们找到了一张新的方式来使用灰度图像，稍后我们可以来谈到。

在应用时，我们主要从以下两个方向来提升病理模型的泛化能力：（1）提升样本的多样性，（2）降低样本的多样性。这两个方向看似矛盾，其实各有道理：

• 提升样本的多样性（increase diversity）：由于病理图像存在染色差异，因此模型可能需要面对色彩高度多样化的测试样本，为了能够应对这些样本，我们应该让训练集覆盖尽量多的色彩情况，即完成色彩增强（Color Augmentation）。这是最常用的方法，只涉及到对训练集进行变化，可以帮助模型对抗过拟合。

具体手段包括：

• 随机仿射变换（随机移动、随机旋转、随机拉伸、随机透视等）
  
• 随机噪声（高斯噪声、脉冲噪声、散粒噪声等）
  
• 随机线性变换（随机亮度、随机对比度、随机色相、随机饱和度、随机色温）
  
• 改变色彩空间（例如，RGB-HSV，基于反卷积的RGB-H&E，RGB-HED等）
  
• 针对单通道的随机线性变换
• 色彩均衡、自动对比度、随机翻转、随机裁剪或填充
  

其中，色彩均衡是将图像直方图（image histogram）标准化为正太分布的操作，图像直方图的横坐标是具体像素值、纵坐标是像素的数量，因此图像直方图绘制的是每个像素值（或像素值区间内）一共有多少个像素。图像直方图一般是分通道绘制的，例如：

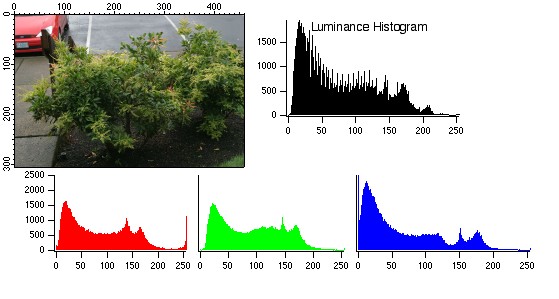
而对比度是该图像上前景与背景的差异，因此一张图上的对比度越高，这张图上的前景与后景的区别会越大。如下所示，左侧是低对比度图像，右侧是高对比度图像：

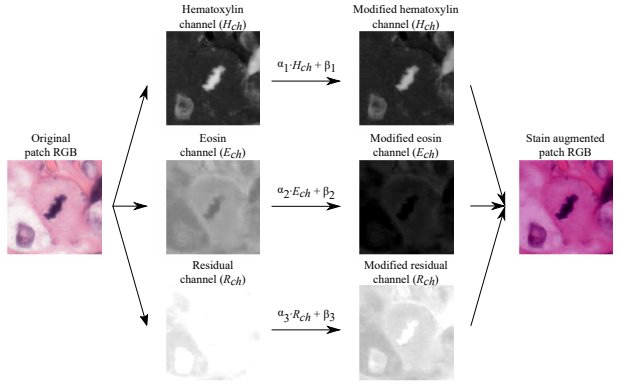
在这些操作当中，在单通道上进行随机加减/乘除运算是目前为止公认效果较好的方式（本质也就是随机调整对比度、亮度等属性），并且一般来说，任意调整的强度都可以作为超参数，在训练过程中被不断调整。在2021年的论文《为H&E染色的组织病理学定制自动数据增强》中，通道层的随机加减/乘除运算被打包成了方法RandAugment，这一方法将所有增强手段“参数化”，可以在训练的过程中自适应调节各类随机变换的数量和变换的程度。同时，2018年的论文《HE染色增强改进了用于组织病理学有丝分裂检测的卷积网络的泛化》提出了全新的思路：将RGB空间修改为H&E空间、在单一色彩空间上随机加减/乘除后，再将色彩空间变回RGB，可有效提升模型泛化能力。

• 降低样本的多样性（decrease diversity）：无论训练集、测试集上的染色有多大差异，只要将整个数据集（包括测试集和验证集）的图像进行色彩标准化（Color Normalization），让所有的图像尽可能在色彩上一致，就可以极大程度降低这种差异带来的影响。这种方法需要对训练集和测试集同时进行修改，也可以帮助模型提升泛化能力。

远在深度学习进入计算机视觉领域之前，研究者们就已经在进行广泛而深入的色彩标准化研究了。在没有深度学习之前，这一方法往往需要先寻找一个“标准图像”作为目标图像，可能是训练集/测试集中提供的某一张图像，也可能是某个实验室标准。找到目标后，再将其他图像按照目标图像进行标准化。因此常见的经典方法有：

• 色彩匹配（Color Matching）：例如Reinhard标准化，使用1998年Ruderman等人发表的论文《锥体对自然图像的反应统计：对视觉编码的影响》（Statistics of cone responses to natural images: implications for visual coding）以及2001年论文《图像之间的颜色转换》中所定义的颜色-对立空间（LAB空间，其中L代表亮度lightness，A代表从绿色到红色的分量，B代表从蓝色到黄色的分量），再定义一张目标图像，对所有图像进行标准化处理。具体的操作是，先将输入图像转换为LAB空间，并以通道为单位，将所有通道的均值中心化至0、再将所有通道的方差缩放为1，然后重新标准化为目标图像统计信息。
  
  
• 染色分离（stain separation）：先使用反卷积手段（如Macenko染色分离、Khan染色分离）将数据集上的染色去除，再使用从目标图像中提取的染色特征向量对去除染色的图像进行卷积，最终生成基于目标图像重新染色的图像。

这些方法简单而有效，但缺点也十分明显：即必须规定一张目标图像。如果该目标图像与需要被标准化的测试数据或验证数据差异太大，那可能会导致标准化后的图像被破坏（比如，变成全黑、全白、轮廓损失等）。现代我们基本都使用深度学习中的生成模型来降低样本多样性，最典型的就是使用各类生成对抗网络（GANs）来完成色彩标准化。

• 基于生成对抗网络（GANs）完成色彩标准化：生成对抗网络GAN是从数据中生成数据的深度学习模型，是当前深度学习领域的研究热点，也是色彩标准化中的SOTA手段。

简单来说，一个GAN包含两个基础网络：生成网络(generator)与判别网络(discriminator)：生成网络用于生成新数据，判别网络用于判断生成的数据和真实数据哪个才是真的。生成网络没有标签，是无监督网络；而判别网络有标签，是有监督网络，其标签是“真与假”（0和1）。与普通二分类网络一样，判别网络输出的是当前数据为假的概率（标签为1的概率），因此概率大于0.5时，判别器认为样本是由生成器生成的假数据，当概率小于0.5时，判别器认为样本是真实数据。

GAN的损失函数是判别网络输出的概率与“真假”这一标签的二分类交叉熵。在训练过程中，生成网络的目标是生成尽量真实的数据（这也是我们对生成对抗网络的要求），让判别网络难以判断，所以生成网络的学习目标是让损失函数越来越大，以此逼迫判别网络的判别能力越来越强；相反，判别网络的目标是尽量判别出真伪，因此判别网络的学习目标是让损失函数越来越小，以此逼迫生成网络生成的数据越来越真。两个网络共享损失函数，此消彼长，是真正的零和博弈。

其中，生成网络可能是基于已有的数据来生成新数据，也可能是基于噪音、甚至随机数来生成新数据。这些新数据就是我们渴望从GAN模型中获取的最终输出，因此GAN是使用有监督方法实现无监督输出的模型。

当将GAN应用于色彩标准化时，我们首先需要两组相互匹配、但染色程度不同的图像A与B，生成网络负责将图像A转变成与图像B高度相似的图像C，判别网络负责判断生成的图像C与原始的图像B哪个才是真实的图像，以此来帮助生成网络生成十分逼真的图像。当图像C与图像B真假难辨的时候，C就是染色程度与B高度相似、但携带A的信息的图像。此时我们使用生成网络输出的图像C来训练卷积神经网络，自然可以避免因实验室不同、色剂不同而导致的染色区别。

但这一手段也有问题，即必须获得两组相匹配的图像A与B，对病理图像来说，这意味着需要使用不同的设备、对同一个载玻片进行2次扫描，甚至需要对一个组织进行2次不同的染色，这样做的成本很高。2017年的论文《使用 GAN处理组织病理学图像的神经染色式迁移学习》提出了一个全新的解决方案，即使用原始彩色载玻片作为图像B，将图像B灰度化后作为图像A，并最终让对抗网络生成与原始图像B高度相似的彩色玻片图像C。这种情况下，由于图像C是从灰度图像生成而来，因此原本的染色差异被削弱了许多，但同时C又与B高度相似，因此又保留了大量原始图像的信息，是非常好的训练材料。

基于这一思想，后来又有多篇论文不断提出了基于复杂的GAN的色彩标准化手段。考虑到深度学习网络本身的复杂程度，基于GAN的色彩标准化也是越来越复杂，在这里我推荐如下几篇，大家可以自行阅读：

基于普通GAN实现的色彩标准化：

[Cho2017] H. Cho, S. Lim, G. Choi, H. Min, Neural stain-style transfer learning using gan for histopathological images (2017), arXiv preprint arXiv:1710.08543

[Salehi2020] P. Salehi, A. Chalechale, Pix2pix-based stain-to-stain translation: A solution for robust stain normalization in histopathology images analysis (2020), International Conference on Machine Vision and Image Processing

基于Cycle-GAN实现的色彩标准化：

[Zhu2017] J.Y. Zhu, T. Park, P. Isola, A.A. Efros, Unpaired image-to-image translation using cycle-consistent adversarial networks (2017), Proceedings of the International Conference on Computer Vision

[Lo2021] Y.C. Lo, I.F. Chung, S.N. Guo, M.C. Wen, C.F. Juang, Cycle-consistent GAN-based stain translation of renal pathology images with glomerulus detection application (2021), Applied Soft Computing

当然了，即便GAN是现在色彩标准化领域的SOTA模型，但基于深度学习的标准化过程不总是最优先的选择，毕竟过于复杂的数据增强流程会极大程度地增加模型的训练成本，因此一般来说，比起使用对抗网络进行数据增强，我们会优先尝试更加简单的预处理方法。在我们的案例当中，我们将使用第三方库imgaug和skimage实现大部分提升多样性（色彩增强）的选项，并使用三方库HistomicsTK以及PyTorch中的DCGAN实现降低多样性（色彩标准化），但考虑到算力与课时原因，最终在建模时我们只会挑选其中的部分手段作为最终手段。

另一个问题是，虽然增加多样性（色彩增强）与降低多样性（色彩标准化）在原理上并不冲突，但最终导致的结果却是相互冲突的，因此在学术界也有大量关于“是否要将色彩增强与色彩标准化同时使用”的讨论。许多论文的结果显示，两者是可以同时使用并提升模型效果的，也有不少论文证明只能二选其一，甚至在某些数据集上，两种方法中只有一种方法能够奏效。面对真实数据时，可以先使用第三方库观察哪种方法对当前数据更有效，然后再选择一个方向进行深入。

4.3 基于imgaug与skimage实现色彩增强（暂空）

4.4 染色标准化入门：GAN、TransposeConv、DCGAN与cGAN

在染色标准化的三大方法之中，使用生成对抗网络GAN进行标准化是原理最复杂、运行成本最高、但效果往往最好的手段。生成对抗网络GAN是由Ian J. Goodfellow及其团队提出，除了这篇被评为“过去10年机器学习领域最有趣的想法”的原始论文《生成对抗网络》之外，Goodfellow等人还是被号称天书的著名深度学习教材花书的第一作者。无论是在花书还是在GAN的论文当中，Goodfellow本人的数学与技术能力都体现得淋漓尽致，但考虑到我们在案例中主要是以实践为核心，因此本次课程中将不会涉及到过于复杂的数学过程。

在生成对抗网络诞生之后数年之中，围绕着如何使用生成对抗网络进行染色标准化的研究层出不穷，今天这些研究中最为代表性的作品是Salehi等人在2020年完成的论文：

[Salehi2020] P. Salehi, A. Chalechale, Pix2pix-based stain-to-stain translation: A solution for robust stain normalization in histopathology images analysis (2020), International Conference on Machine Vision and Image Processing

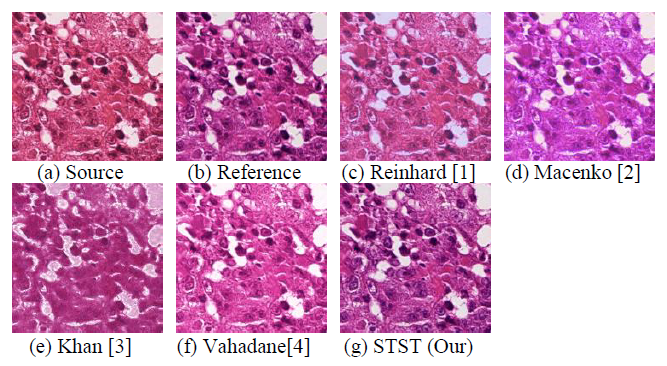
这篇论文在经典对抗架构Pix2Pix的基础上做出了改进，创造出架构Stain-to-Stain Translation（STST），并成功实现了目前为止效果最优的染色标准化。如下图所示，a为原始染色载玻片，b为参考用的染色载玻片，c-g为使用不同方式实现染色标准化的生成图像。从颜色、轮廓等各个角度来看，STST的表现肉眼可见地超越了其他经典的染色标准化方法。

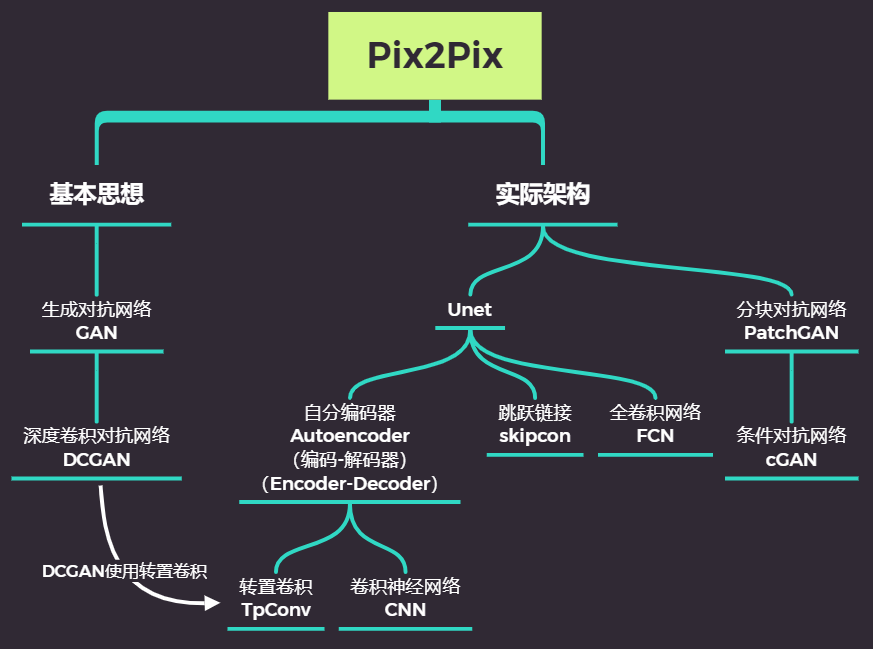
在本次我们的课程当中，我们将尝试复现上述论文中的STST架构，并尝试实现基于STST的染色标准化方法。STST架构是基于Pix2Pix2改进而来，而Pix2Pix是由如下基本架构组成：

因此，为了掌握最终的STST架构，我们需要掌握如下基础知识：

1. 原始GAN的运行原理与代码
   
2. 转置卷积TransposedConv与能够处理图像的DCGAN
   
3. 自动编码器Autoencoders，经典Encoder-Decoder架构
   
4. 深度卷积自动编码器（Convolutional Autoencoders）架构
   
5. cGAN与PatchGAN架构
   
6. Unet的损失函数、运行原理与代码
   
7. STST架构基于Unet做出了怎样的改进
   

在此之后，我们才能够将STST架构用于染色标准化。以上基础知识当中，你可以选择你不了解的部分进行学习，如果你已了解全部相关内容，可以直接从第7部分开始进行学习。

4.4.1 GAN的基本原理与损失函数

我们先来复习一下GAN的基本概况。假设现在存在一组从真实场景中收集的数据RealData，生成对抗网络的关键使用场景之一就是借助真实数据RealData生成一组假数据FakeData，且这组假数据最好能够以假乱真。有时候这组生成的假数据会用于替代真实数据或加入真实数据、用于训练神经网络，有时候这组生成的假数据就是我们最终想要获得的目标（例如，AI生成人脸的技术）。因此大部分时候，生成对抗网络的最终目标就是输出一组以假乱真的假数据。

如下图所示，一个生成对抗网络包含两个基础网络：生成器(generator，简写为G，也被称为生成网络)与判别器(discriminator，简写为D，也被称为判别网络)。其中，生成器用于生成新数据，其生成数据的基础往往是一组噪音或者随机数，而判别器用于判断生成的数据和真实数据哪个才是真的。生成器没有标签，是无监督网络；而判别器有标签，是有监督网络，其标签是“假与真”（0与1）。与普通二分类网络一样，判别器输出的是一类标签下的概率。在GAN官方论文中，我们规定判别器输出当前数据为真的概率（标签为1的概率），因此概率大于0.5时，判别器认为样本是真实数据，当概率小于0.5时，判别器认为样本是由生成器生成的假数据。

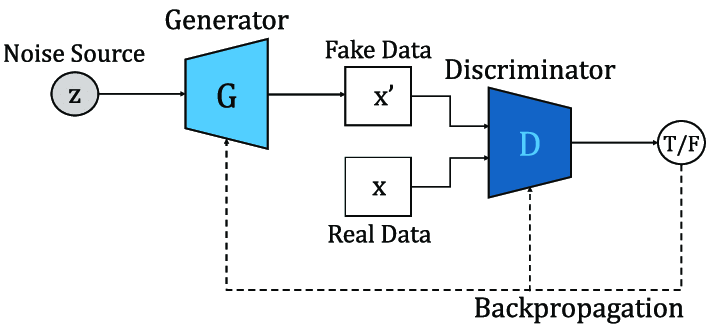
在训练过程中，生成器和判别器的目标是相矛盾的，并且这种矛盾可以体现在判别器的判断准确性上。生成器的目标是生成尽量真实的数据（这也是我们对生成对抗网络的要求），最好能够以假乱真、让判别器判断不出来，因此生成器的学习目标是让判别器上的判断准确性越来越低；相反，判别器的目标是尽量判别出真伪，因此判别器的学习目标是让自己的判断准确性越来越高。

当生成器生成的数据越来越真时，判别器为维持住自己的准确性，就必须向判别能力越来越强的方向迭代。当判别器越来越强大时，生成器为了降低判别器的判断准确性，就必须生成越来越真的数据。在这个奇妙的关系中，判别器判断的准确性由GAN论文中定义的特殊交叉熵$V$来衡量，判别器与生成器共同影响交叉熵$V$，同时训练、相互内卷，对该交叉熵的控制是此消彼长的，这是真正的零和博弈。

• 特殊交叉熵$V$

在生成器与判别器的内卷关系中，GAN的特殊交叉熵公式如下：

$$V(D,G)=\frac{1}{m}\sum _{i=1}^m[logD(x_i)+log(1-D(G(z_i)))]$$

其中，字母$V$是原始GAN论文中指定用来表示该交叉熵的字母，对数log的底数为自然底数e，$m$表示共有$m$个样本，因此以上表达式是全部样本交叉的均值表达式。除此之外，$x_i$表示任意真实数据，$z_i$表示与真实数据相同结构的任意随机数据，$G(z_i)$表示在生成器中基于$z_i$生成的假数据，而$D(x_i)$表示判别器在真实数据$x_i$上判断出的结果，$D(G(z_i))$表示判别器在假数据$G(z_i)$上判断出的结果，其中$D(x_i)$与$D(G(z_i))$都是样本为“真”的概率，即标签为1的概率。

在原始论文中，这一交叉熵被认为是一种“损失”（Loss），但它有两个特殊之处：

1）不同于二分类交叉熵等常见的损失函数，损失$V$上不存在最小值，反而存在最大值。具体来看，$D(x_i)$与$D(G(z_i))$都是概率，因此这两个值的范围都在(0,1)之间。对于底数为$e$的对数函数来说，在定义域在(0,1)之间意味着函数的值域为($-\infty$,0)。因此理论上来说，损失$V$的值域也在($-\infty$,0)。

2）损失$V$在判别器的判别能力最强时达到最大值，这就是说判别器判断得越准确时、损失反而越大，这违背我们对普通二分类网络中的损失函数的期待。但如果我们从判别器和生成器角度分别来看待公式$V$，则可以很快理解这一点。

• 判别器的角度

不难发现，在V的表达式中，两部分对数都与判别器D有关，而只有后半部分的对数与生成器G有关。因此我们可以按如下方式分割损失函数：

对判别器我们有：
$$Los{s}_D=\frac{1}{m}\sum _{i=1}^m[logD(x_i)+log(1-D(G(z_i)))]$$

从判别器的角度来看，由于判别器希望自己尽量能够判断正确，而输出概率又是“数据为真”的概率，所以最佳情况就是所有的真实样本上的输出$D(x_i)$都无比接近1，而所有的假样本上的输出$D(G(z_i))$都无比接近0。因此对判别器来说，最佳损失值是：

$$\begin{array}{rl}Los{s}_D& =\frac{1}{m}\sum _{i=1}^m[logD(x_i)+log(1-D(G(z_i)))]\\ & =\frac{1}{m}\sum _{i=1}^m[log1+log(1-0)]\\ & =0\end{array}$$

这说明判别器希望以上损失$Los{s}_D$越大越好，且最大值理论上可达0，且判别器追求大$Los{s}_D$的本质是令$D(x)$接近1，令$D(G(z))$接近0。不难发现，对判别器而言，$V$更像是一个存在上限的积极的指标（比如，准确率），即算法表现越好时，该指标的值越高。

• 生成器的角度

而从生成器的角度来看，生成器无法影响$D(x_i)$，只能影响$D(G(z_i))$，因此只有损失的后半段与生成器相关。因此对生成器我们有：

$$\begin{array}{rl}Los{s}_G& =\frac{1}{m}\sum _{i=1}^m[常数+log(1-D(G(z_i))]\\ 去掉无关的常数部分：& \to \frac{1}{m}\sum _{i=1}^{m}log(1-D(G(z_i))\end{array}$$

生成器的目标是令输出的数据越真越好，最好让判别器完全判断不出，因此生成器希望$D(G(z_i))$越接近1越好。因此对生成器来说，最佳损失是：

$$\begin{array}{rl}Los{s}_G& =\frac{1}{m}\sum _{i=1}^m[log(1-D(G(z_i))]\\ & =\frac{1}{m}\sum _{i=1}^m[log(1-1)]\\ & =-\infty \end{array}$$

这说明生成器希望以上损失$Los{s}_G$越小越好，且最小值理论上可达负无穷，且生长期追求小$Los{s}_G$的本质是令$D(G(z))$接近1。对生成器而言，$V$更像是一个损失，即算法表现越好，该指标的值越低。从整个生成对抗网络的角度来看，我们（使用者）的目标与生成器的目标相一致，因此对我们而言，$V$被定义为损失，它应该越低越好。

• 原始论文中的表示方法

在原始论文当中，该损失$V$被表示为如下形式：

$$\underset{G}{\min }\underset{D}{\max }V(D,G)={\mathbb{E}}_{x\sim p_{data}(x)}[logD(x)]+{\mathbb{E}}_{z\sim p_z(z)}[log(1-D(G(z)))]$$

即先从判别器的角度令损失最大化，又从生成器的角度令损失最小化，即可让判别器和生成器在共享损失的情况下实现对抗。其中$E$表示期望，第一个期望${\mathbb{E}}_{x\sim p_{data}(x)}[logD(x)]$是所有$x$都是真实数据时$logD(x)$的期望，第二个期望${\mathbb{E}}_{z\sim p_z(z)}[log(1-D(G(z)))]$是所有数据都是生成数据时$log(1-D(G(z)))$的期望。当真实数据、生成数据的样本点固定时，期望就等于均值。因此论文中的这个式子与我们之前所写的、在损失前面乘以$\frac{1}{m}$在数学计算上并无区别。

如此，通过共享以上损失函数，生成器与判别器实现了在训练过程中互相对抗，$\underset{G}{\min }\underset{D}{\max }V(D,G)$的本质就是最小化$Los{s}_G$的同时最大化$Los{s}_D$。并且，在最开始训练时，由于生成器生成的数据与真实数据差异很大，因此$D(x_i)$应该接近1，$D(G(z_i))$应该接近0。理论上来说，只要训练顺利，最终$D(x_i)$和$D(G(z_i))$都应该非常接近0.5，但现实总不会那么地完美。在实际使用生成对抗网络时，生成器无法战胜判别器是很常见的情况，因此现在有各类的研究都在努力尝试提升生成器的生成水平，我们案例中所涉及的染色标准化的相关研究也是提升生成器性能的研究之一。

4.4.2 详解基础GAN架构与反向传播代码

• 定义判别器与生成器

在最原始的GAN论文当中，生成器和判别器都是最普通的、以线性层构成的神经网络。如果你足够熟悉神经网络基础，那你一定会注意到生成对抗网络中的生成器、判别器两大网络都可以以非常简单的方式实现，例如我们可以假设生成器与判别器中都只有最为简单的2个线性层，其中激活函数都为LeakyReLU。为完成二分类，判别器的输出函数为sigmoid，生成器由于不需要完成分类任务、只需要输出结果，因此原则上不需要输出函数，但考虑到大部分时候我们所使用的都是图像数据、而图像数据是有界的数据，因此在生成器的最后我们会加上一个用于将数据归一化到固定范围的输出函数，大部分时候这个输出函数是Tanh。

同时，生成器生成的数据FakeData需要输入判别器，因此判别器的in_features参数必须与生成器的输出的out_features一致。对于判别器而言，除了输入生成器生成的FakeData之外，还需要接受真实数据RealData的输入，因此一般我们默认FakeData的结构与RealData完全一致。