【图文详解】强化学习核心框架、数学基础、分类、应用场景

• 若对您有帮助的话，请点赞收藏加关注哦，您的关注是我持续创作的动力！有问题请私信或联系邮箱：[e-mail]

强化学习（Reinforcement Learning, RL）是机器学习的三大核心范式之一（另外两者为监督学习、无监督学习），其本质是智能体（Agent）通过与环境（Environment）的持续交互试错，学习“如何选择动作以最大化累积奖励”的决策策略。与监督学习依赖“输入-标签”的静态数据、无监督学习聚焦数据结构不同，强化学习的核心是“动态交互”与“延迟奖励”——智能体需在不确定环境中探索，且奖励可能在多步动作后才反馈（如游戏中“击败BOSS”的奖励需先完成多轮战斗）。

一、强化学习的核心框架：基本要素与交互流程

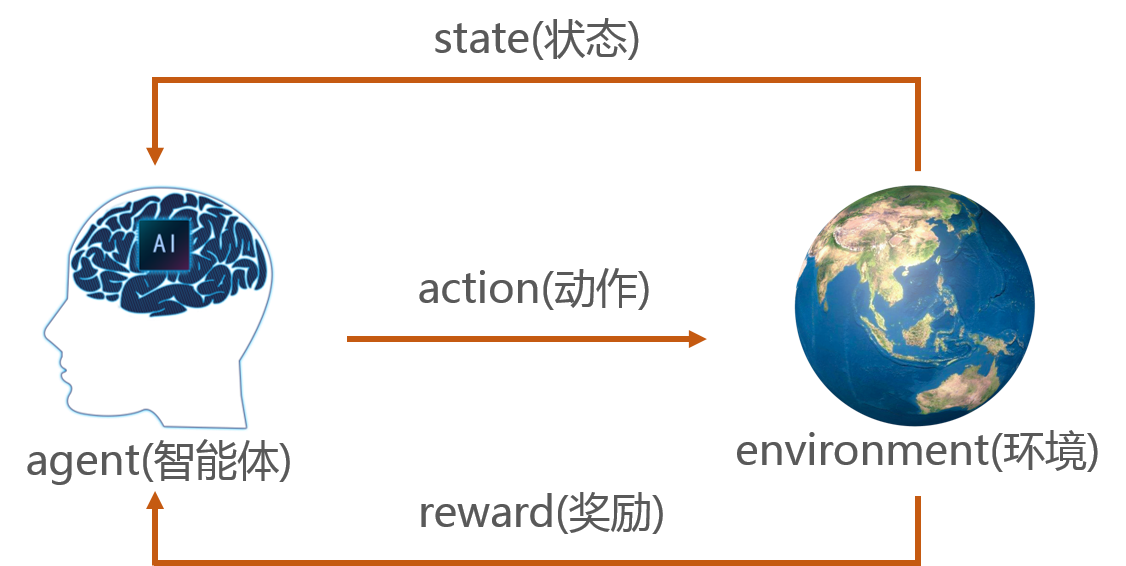
强化学习的运作可抽象为“智能体-环境”的循环交互，核心包含6个要素，共同构成决策闭环：

核心要素	定义与作用	示例（以“机器人走迷宫”为例）
智能体（Agent）	执行决策的主体（如AI模型、机器人），具备“感知环境”“选择动作”“更新策略”的能力	走迷宫的机器人（内置RL模型）
环境（Environment）	智能体交互的外部场景，状态随智能体动作动态变化，且可能存在随机性	迷宫本身（包含墙壁、终点、陷阱等固定元素，及随机出现的障碍物）
状态（State, S）	环境的当前信息快照，是智能体决策的依据（需包含“影响未来奖励的关键信息”）	机器人当前坐标（如(3,4)）、周围是否有墙壁、是否靠近终点
动作（Action, A）	智能体可执行的操作，分为“离散动作”（如上下左右）和“连续动作”（如机械臂角度）	机器人的4个方向移动（上/下/左/右）
奖励（Reward, R）	环境对智能体动作的即时反馈（正奖励/负奖励/零奖励），是策略优化的“指挥棒”	靠近终点+10分，撞到墙壁-5分，到达终点+100分，陷阱-50分
策略（Policy, π）	智能体的“决策规则”，定义“在某状态下选择某动作的概率”（如π(a	s)表示状态s选动作a的概率）

交互流程（循环闭环）

1. 初始化：环境生成初始状态（如机器人在迷宫起点(1,1)），智能体加载初始策略；
2. 感知与决策：智能体获取当前状态Sₜ，通过策略π选择动作Aₜ；
3. 执行与反馈：环境接收动作Aₜ，转移到新状态Sₜ₊₁，并返回即时奖励Rₜ₊₁；
4. 学习更新：智能体根据“状态Sₜ→动作Aₜ→奖励Rₜ₊₁→新状态Sₜ₊₁”的经验，更新策略π（让未来更可能选择获得高奖励的动作）；
5. 终止判断：若Sₜ₊₁是“终止状态”（如机器人到达终点或掉入陷阱），则结束一轮交互（称为“一个回合，Episode”）；否则回到步骤2，开始下一轮交互。

二、强化学习的数学基础：马尔可夫决策过程（MDP）

几乎所有强化学习问题都可建模为马尔可夫决策过程（Markov Decision Process, MDP），其核心是“马尔可夫性”——未来状态仅依赖当前状态，与历史状态无关（如机器人下一步的位置仅取决于当前位置和动作，与之前走的路径无关）。MDP是强化学习算法设计的理论基石，形式化定义为一个五元组（S, A, P, R, γ）：

• 状态空间S：所有可能状态的集合（如迷宫中所有坐标的集合）；
• 动作空间A：所有可能动作的集合（如4个移动方向）；
• 状态转移概率P：P(s’|s,a)表示“在状态s执行动作a后，转移到状态s’的概率”（若环境确定，P为0或1；若环境随机，P为概率分布，如10%概率遇到随机障碍物）；
• 奖励函数R：R(s,a,s’)表示“从状态s经动作a转移到s’的即时奖励”（也可简化为R(s,a)，仅与当前状态和动作相关）；
• 折扣因子γ（0≤γ≤1）：平衡“短期奖励”与“长期奖励”的权重——γ=0时仅关注即时奖励（短视），γ=1时同等重视未来所有奖励（远视），实际应用中γ常取0.9~0.99（如游戏AI需兼顾“当前清兵”和“最终推塔”）。

三、强化学习的核心目标：最大化累积奖励

智能体的最终目标不是“单次动作奖励最大化”，而是“长期累积奖励最大化”。常用的累积奖励定义有两种：

1. 回合累积奖励（Return, Gₜ）：在第t步后，未来所有奖励的加权和，即
   $$G_t=R_{t+1}+\gamma R_{t+2}+{\gamma }^2{R}_{t+3}+...+{\gamma }^{T-t-1}{R}_T$$
   其中T是回合终止步数（如机器人到达终点的步数），γ^k表示“k步后奖励的折扣系数”（未来越远的奖励，权重越低）。
2. 价值函数（Value Function）：衡量“某状态/动作的长期价值”，是策略优化的核心工具，分为两类：
   • 状态价值函数V^π(s)：在策略π下，从状态s出发的期望累积奖励（“状态s好不好”），即
     $$V^{\pi }(s)={\mathbb{E}}_{\pi }[G_t|S_t=s]$$
   • 动作价值函数Q^π(s,a)：在策略π下，从状态s执行动作a后，后续遵循π的期望累积奖励（“在状态s选动作a好不好”），即
     $$Q^{\pi }(s,a)={\mathbb{E}}_{\pi }[G_t|S_t=s,A_t=a]$$

强化学习的本质就是寻找最优策略π*，使得对所有状态s，V^π*(s) ≥ V^π(s)（或Qπ*(s,a) ≥ Q^π(s,a)），即最优策略下的长期价值高于任何其他策略。

四、强化学习的主要算法分类

根据“是否依赖价值函数”“是否直接优化策略”，强化学习算法可分为三大类，各类算法的核心思想、适用场景差异显著：

1. 价值-based算法（Value-Based RL）

• 核心思想：不直接优化策略，而是先学习“最优动作价值函数Q*(s,a)”（即最优策略下的Q值），再通过Q*(s,a)推导最优策略（如在状态s选择Q值最大的动作）。
• 关键假设：动作空间是离散的（若动作连续，Q值无法枚举所有动作）。
• 代表算法：

  • Q-Learning（异策略算法）：

    • 核心逻辑：通过“时序差分（TD）更新”学习Q值，即利用“当前Q值”和“下一个状态的最大Q值”修正，公式为：
      $$Q(s,a)\leftarrow Q(s,a)+\alpha \left[R+\gamma \underset{a^{\prime }}{\max }Q(s^{\prime },a^{\prime })-Q(s,a)\right]$$
      其中α是学习率（控制更新幅度，0<α<1），“max_{a’} Q(s’,a’)”表示下一个状态s’的最优动作Q值（不依赖当前策略，因此是“异策略”）。
    • 优势：不依赖下一个动作的实际选择，样本利用效率高；
    • 劣势：仅适用于离散动作，无法处理连续动作（如机械臂的角度控制）。

  • SARSA（同策略算法）：

    • 与Q-Learning的核心差异：更新Q值时，使用“下一个状态s’实际选择的动作a’的Q值”（而非最大Q值），公式为：
      $$Q(s,a)\leftarrow Q(s,a)+\alpha \left[R+\gamma Q(s^{\prime },a^{\prime })-Q(s,a)\right]$$
    • 优势：更保守（考虑实际执行的动作），适合需要安全性的场景（如机器人避障）；
    • 劣势：样本效率低于Q-Learning，同样仅适用于离散动作。

  • Deep Q-Network（DQN，深度Q网络）：

    • 核心创新：用深度神经网络（如CNN）拟合Q(s,a)（解决高维状态问题，如游戏画面），并引入两大技术解决训练不稳定问题：
      1. 经验回放（Replay Buffer）：将交互经验（s,a,R,s’）存储到缓冲区，随机采样训练，打破样本的时间相关性；
      2. 目标网络（Target Network）：单独维护一个“目标Q网络”，用于计算“R + γ max_{a’} Q_target(s’,a’)”，每隔固定步数同步到主网络，避免Q值更新震荡。
    • 里程碑：2013年DeepMind用DQN在Atari游戏（如打砖块、乒乓球）中达到人类水平，标志强化学习进入“深度强化学习（DRL）”时代。

2. 策略-based算法（Policy-Based RL）

• 核心思想：不学习价值函数，而是直接参数化策略（如用神经网络π_θ(a|s)，θ为网络参数），通过梯度上升最大化“策略的期望累积奖励”，即最大化J(θ) = E_π_θ[G₀]。
• 适用场景：连续动作空间（如自动驾驶的方向盘角度、油门大小），或动作空间极多的场景（如围棋的10^170种动作）。
• 代表算法：

  • 策略梯度（Policy Gradient, PG）：

    • 核心逻辑：通过计算“期望累积奖励对策略参数θ的梯度”∇θ J(θ)，沿梯度方向更新θ，使策略更可能选择高奖励动作。梯度公式推导后可简化为：
      $${\nabla }_{\theta }J(\theta )\approx {\mathbb{E}}_{\pi }\left[\sum _{t=0}^{T-1}{\nabla }_{\theta }\log {\pi }_{\theta }(a_t|s_t)\cdot G_t\right]$$
    • 优势：天然支持连续动作，策略输出直接是动作概率（或动作值）；
    • 劣势：训练方差大（奖励波动导致梯度不稳定），样本效率低（每轮交互后需重新采样）。

  • 优势演员-评论员（Advantage Actor-Critic, A2C）：

    • 核心改进：结合“策略网络（Actor，演员）”和“价值网络（Critic，评论员）”——
      1. Actor：负责输出策略π_θ(a|s)，通过梯度上升优化；
      2. Critic：负责学习价值函数V_φ(s)，计算“优势函数A(s,a) = Q(s,a) - V(s)”（衡量动作a相对于当前状态平均价值的“超额价值”），用A(s,a)替代PG中的G_t，减少方差。
    • 优势：方差显著降低，训练更稳定；
    • 变种：A3C（异步A2C），通过多线程并行采样，提升训练速度。

  • 近端策略优化（Proximal Policy Optimization, PPO）：

    • 核心解决：PG算法中“策略更新步长过大导致训练崩溃”的问题，通过“剪辑目标函数”限制策略更新幅度，公式为：
      $$L_{CLIP}(\theta )={\mathbb{E}}_t\left[\min \left(r_t(\theta )A_t,\text{clip}(r_t(\theta ),1-ϵ,1+ϵ)A_t\right)\right]$$
      其中r_t(θ) = π_θ(a_t|s_t)/π_θ_old(a_t|s_t)（新旧策略的概率比），ε通常取0.2（限制r_t在0.8~1.2之间）。
    • 地位：目前工业界最常用的强化学习算法之一，兼顾稳定性、样本效率和实现难度，广泛用于机器人控制、游戏AI、推荐系统。

3. 模型-based算法（Model-Based RL）

• 核心思想：先学习“环境模型”（即估计状态转移概率P和奖励函数R），再基于环境模型“规划”最优动作（如通过动态规划计算最优策略），无需与真实环境大量交互。
• 优势：样本效率极高（仅需少量交互学习模型）；
• 劣势：环境模型的误差会累积（如模型估计的P与真实P偏差，导致规划结果失效），仅适用于环境变化缓慢、可建模的场景（如棋类游戏）。
• 代表算法：Dyna（结合模型学习与模型-free更新）、世界模型（World Models，用生成模型拟合环境）。

五、强化学习的关键技术与挑战

1. 核心技术（解决训练痛点）

• 探索与利用（Exploration-Exploitation Trade-off）：

  • 探索（Exploration）：尝试新动作，可能发现更高奖励（如机器人尝试未走过的路径）；
  • 利用（Exploitation）：选择已知Q值最高的动作，获取确定奖励（如机器人重复走已知的近路）；
  • 解决方法：ε-贪心策略（以ε概率随机探索，1-ε概率利用）、UCB（Upper Confidence Bound，对不确定的动作赋予更高权重）。

• 经验回放（Replay Buffer）：

  • 作用：存储历史交互经验，随机采样训练，打破样本的时间相关性（避免模型学到“时序噪声”），同时复用样本（提升效率）；
  • 适用场景：所有价值-based算法（如DQN）和部分AC算法（如PPO）。

• 目标网络（Target Network）：

  • 作用：固定“目标Q值”的计算基准，避免Q值更新时“当前Q值和目标Q值同时波动”导致的训练震荡；
  • 机制：主网络负责更新参数，目标网络每隔N步（如1000步）从主网络复制参数。

2. 主要挑战（当前研究热点）

• 样本效率低：模型-free算法（如PPO、DQN）需与环境交互百万级甚至亿级样本才能收敛（如训练一个自动驾驶模型需模拟千万公里行驶），难以应用于物理世界（如真实机器人交互成本高）；

  • 解决方案：离线强化学习（Offline RL，用已有数据集训练，无需实时交互）、迁移学习（将仿真环境的模型迁移到真实环境）。

• 泛化能力差：模型在训练环境中表现优异，但在微小变化的新环境中性能骤降（如机器人在“干净地板”上训练好的走路模型，在“地毯”上无法稳定行走）；

  • 解决方案：多环境训练（Domain Randomization）、元强化学习（Meta-RL，学习“快速适应新环境的能力”）。

• 安全性与可解释性：强化学习通过“试错”学习，可能执行危险动作（如机器人碰撞障碍物、金融AI做出高风险交易），且策略决策过程难以解释（“黑箱”问题）；

  • 解决方案：约束强化学习（Constrained RL，限制动作在安全范围内）、可解释AI（XAI）与RL结合。

六、强化学习的典型应用场景

1. 游戏领域：

   • AlphaGo（DeepMind，2016）：结合强化学习与蒙特卡洛树搜索，击败世界围棋冠军李世石；
   • OpenAI Five（2019）：用PPO算法训练的DOTA2 AI，击败世界顶级职业战队；
   • 王者荣耀AI、和平精英AI：通过强化学习优化团战策略、资源分配。

2. 机器人与控制：

   • 自动驾驶：强化学习优化“车道保持”“超车决策”“紧急避障”（如特斯拉的Autopilot部分模块）；
   • 机械臂：学习高精度抓取、装配动作（如富士康用RL训练机械臂组装手机）；
   • 无人机：自主规划路径、避障（如大疆无人机的“智能跟随”功能）。

3. 推荐系统：

   • 动态推荐：根据用户实时行为（如点击、停留时长）调整推荐策略，最大化长期用户留存（如抖音、淘宝的推荐算法）；
   • 个性化定价：通过强化学习平衡“用户付费意愿”与“平台收益”（如网约车动态定价）。

4. 金融与工业：

   • 量化交易：学习股票、期货的买卖时机，最大化收益（需结合风险约束）；
   • 工业控制：优化化工生产流程、电网调度，降低能耗（如国家电网用RL优化负荷分配）。

七、总结与发展趋势

强化学习的核心是“从交互中学习最优决策”，其优势在于处理“动态、不确定、延迟奖励”的复杂决策问题，是实现通用人工智能（AGI）的关键路径之一。当前，强化学习正朝着以下方向发展：

1. 大模型与RL结合：用GPT等大语言模型（LLM）作为智能体的“大脑”，提升环境理解和动作规划能力（如Google的SayCan、OpenAI的GPT-4+RL）；
2. 多智能体强化学习（MARL）：研究多个智能体的协作与竞争（如自动驾驶中的多车协同、机器人团队协作）；
3. 离线强化学习（Offline RL）：突破“实时交互”限制，利用历史数据训练，加速在医疗、金融等高成本场景的应用；
4. 安全与对齐（AI Alignment）：确保强化学习的目标与人类利益一致（如避免AI为追求奖励而忽视人类安全）。

随着算法效率的提升和硬件算力的增强，强化学习将在更多领域落地，从“游戏AI”走向“解决现实世界的复杂决策问题”。