算法 --- 多源 BFS
多源 BFS
多源BFS适用于这样一种题目类型:问题要求你从一个或多个‘源点’出发,找到到达某个或某一类‘目标’的最短路径,并且这些源点不是单一的,而是多个的、等效的起点。
详细解释
多源BFS的经典应用场景是 “多点起源,同步扩散,寻找最近目标” 的问题。当你的问题模型符合以下特征时,就应考虑使用多源BFS:
-
多个起点:你不是从地图上的一个点开始,而是从一组性质相同的点开始(例如,多个火源、多个敌人、多个入口)。
-
寻找最短路径:核心问题仍然是求最短距离或最短时间,但这个“最短”是相对于所有起点而言的。常见的问题有:
-
到最近目标的距离:求地图中每个点离它最近的起点的距离(如“地图分析”、“腐烂的橘子”)。
-
目标到任意起点的最短距离:求一个或多个目标点,离任意一个起点的最近距离(如“迷宫入口”问题)。
-
-
等效扩散:所有起点在BFS扩散时的行为和优先级是相同的,可以视为一个整体。
什么题目适用于多源BFS?
核心判断标准:问题是否在本质上等价于“从所有源点同时开始进行BFS遍历”。
典型的题目类型和例子:
-
距离映射问题
-
题目:像“地图分析”(1162. As Far from Land as Possible),给你一个网格,其中有1(陆地)和0(海洋),要求找到每一个海洋格子到最近的陆地格子的距离,然后所有距离中的最大值。
-
为什么适用:这里的“多个源点”就是所有的陆地格子(1)。我们不是从一个陆地开始找海洋,而是从所有陆地同时开始BFS,向外扩散(想象成洪水从所有陆地同时蔓延)。这样,当海水(0)第一次被某块陆地蔓延过来的洪水碰到时,这个距离就是它到最近陆地的距离。这比从每个海洋出发做BFS去找陆地要高效无数倍。
-
-
多点状态传播问题
-
题目:像“腐烂的橘子”(994. Rotting Oranges),网格中有新鲜橘子、腐烂橘子和空格子。每一分钟,腐烂橘子会使其上下左右的新鲜橘子腐烂。问需要多久所有橘子都会腐烂,或者返回不可能。
-
为什么适用:这里的“多个源点”就是所有初始的腐烂橘子。我们不是从一个腐烂橘子开始计算时间,而是从所有腐烂橘子同时开始BFS。每一分钟(即BFS的每一层),它们会共同感染周围的新鲜橘子。这样,当我们完成BFS后,遍历的层数(时间)就是全部腐烂所需的时间,并且可以很方便地检查最后是否还有未被访问到的新鲜橘子。
-
-
多入口/多目标最短路径问题
-
题目:在一个迷宫中,有多个入口(起点)和一个宝藏(目标),求从任意一个入口到宝藏的最短路径。
-
为什么适用:我们可以将所有入口点都作为初始源点加入BFS队列,然后开始扩散。谁先碰到宝藏,谁所代表的路径就是最短路径。这避免了为每个入口单独运行一次BFS。
-
算法实现上的关键点:
与单源BFS的唯一区别在于初始化队列:
-
单源BFS:将单个起点加入队列。
-
多源BFS:将所有起点都加入队列,并且视它们的距离(或时间)为0(同一层),然后正常进行BFS即可。
这种方法保证了BFS的层次遍历特性依然成立,每次扩散都代表距离增加1,从而高效地计算出所有点到最近源点的最短距离。
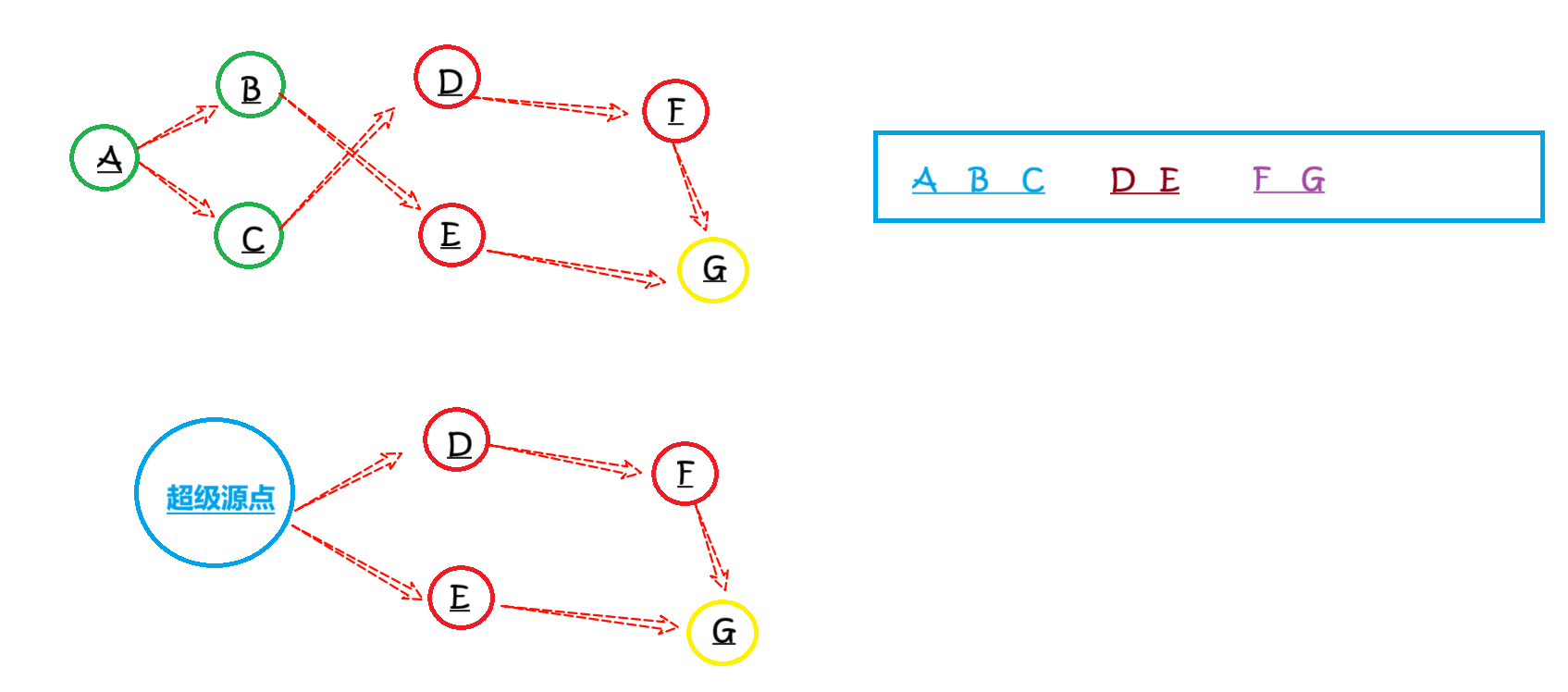
超级源点 / 汇点 概念:
超级源点 / 汇点是模拟出来的虚拟点,多用于图中:
- 同时有多个源点和多个汇点,建立超级源点和超级汇点
- 同时有多个源点和一个汇点,建立超级源点
- 同时有多个汇点和一个源点,建立超级汇点
总结:源点和汇点哪个有多个,就开哪个的超级点
我们平时所做的算法多是适用于一个源点到一个汇点或者是一个源点到多个汇点的类型,但是如果出现多个源点对应多个汇点时,我们会不知所措。跑多遍算法?那样会 TLE,换个思维,既然是从多个源点出发到多个汇点,我们能不能建立一个点来代替多个源点 / 汇点的效果,而又不影响答案。
当我们具有多个源点和一个汇点,我们要求源点到汇点的最短路径,则可以建立一个超级源点,连接所有源点,并且路径长度为 0,然后只需要跑超级源点到汇点这 (n+1) 个点的最短距离即可
题目练习
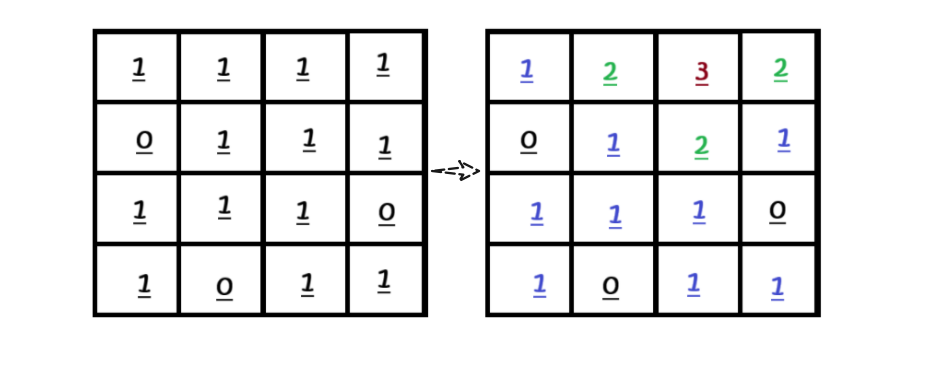
542. 01 矩阵 - 力扣(LeetCode)
解法(bfs)(多个源头的最短路问题)
算法思路:
对于求的最终结果,我们有两种方式:
-
第一种方式:从每一个 1 开始,然后通过层序遍历找到离它最近的 0 。
这一种方式,我们会以所有的 1 起点,来一次层序遍历,势必会遍历到很多重复的点。并且如果矩阵中只有一个 0 的话,每一次层序遍历都要遍历很多层,时间复杂度较高。
-
换一种方式:从 0 开始层序遍历,并且记录遍历的层数。当第一次碰到 1 的时候,当前的层数就是这个 1 离 0 的最短距离。
这一种方式,我们在遍历的时候标记一下处理过的 1,能够做到只用遍历整个矩阵一次,就能得到最终结果。
但是,这里有一个问题,0 是有很多个的,我们怎么才能保证遇到的第一个 1 距离这一个 0 是最近的呢?
其实很简单,我们可以先把所有的 0 都放在队列中,把它们当成一个整体,每次把当前队列里面的所有元素向外扩展一次。
class Solution {
public:int dx[4] = {1, -1, 0, 0};int dy[4] = {0, 0, 1, -1};vector<vector<int>> updateMatrix(vector<vector<int>>& mat) {int m = mat.size(), n = mat[0].size();vector<vector<int>> dist(m, vector<int>(n, -1));queue<pair<int, int>> q;for(int i = 0; i < m; ++i)for(int j = 0; j < n; ++j)if(mat[i][j] == 0){q.push({i, j});dist[i][j] = 0;}while(q.size()){auto [a, b] = q.front();q.pop();for(int k = 0; k < 4; ++k){int x = a + dx[k], y = b + dy[k];if(x >= 0 && x < m && y >= 0 && y < n && dist[x][y] == -1){dist[x][y] = dist[a][b] + 1;q.push({x, y});}}}return dist;}
};
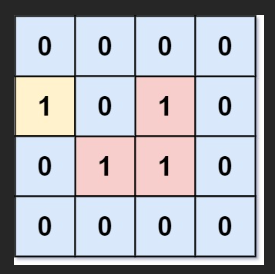
1020. 飞地的数量 - 力扣(LeetCode)
解法:
算法思路:
正难则反:
从边上的 1 开始搜索,把与边上 1 相连的联通区域全部标记一下;
然后再遍历一遍矩阵,看看哪些位置的 1 没有被标记即可。
标记的时候,可以用「多源 bfs」解决。
class Solution {
public:int dx[4] = {1, -1, 0, 0};int dy[4] = {0, 0, 1, -1};int numEnclaves(vector<vector<int>>& grid) {int m = grid.size(), n = grid[0].size();vector<vector<bool>> vis(m, vector<bool>(n, false));queue<pair<int, int>> q;for(int i = 0; i < m; ++i){if(grid[i][0] == 1) q.push({i, 0});if(grid[i][n - 1] == 1) q.push({i, n - 1});}for(int j = 0; j < n; ++j){if(grid[0][j] == 1) q.push({0, j});if(grid[m - 1][j] == 1) q.push({m - 1, j});}while(q.size()){auto [a, b] = q.front();q.pop();vis[a][b] = true;for(int k = 0; k < 4; ++k){int x = a + dx[k], y = b + dy[k];if(x >= 0 && x < m && y >= 0 && y < n && !vis[x][y] && grid[x][y] == 1){vis[x][y] = true;q.push({x, y});}}}int ret = 0;for(int i = 0; i < m; ++i){for(int j = 0; j < n; ++j){if(grid[i][j] == 1 && !vis[i][j]) ret++;}}return ret;}
};
1765. 地图中的最高点 - 力扣(LeetCode)
解法:
算法思路:
01矩阵的变型题,直接用多源 bfs解决即可。
class Solution {
public:int dx[4] = {1, -1, 0, 0};int dy[4] = {0, 0, 1, -1};vector<vector<int>> highestPeak(vector<vector<int>>& isWater) {int m = isWater.size(), n = isWater[0].size();vector<vector<int>> dist(m, vector<int>(n, -1));queue<pair<int, int>> q;for(int i = 0; i < m; ++i)for(int j = 0; j < n; ++j)if(isWater[i][j] == 1){q.push({i, j});dist[i][j] = 0;}while(q.size()){auto [a, b] = q.front();q.pop();for(int k = 0; k < 4; ++k){int x = a + dx[k], y = b + dy[k];if(x >= 0 && x < m && y >= 0 && y < n && dist[x][y] == -1){dist[x][y] = dist[a][b] + 1;q.push({x, y});}}}return dist;}
};
1162. 地图分析 - 力扣(LeetCode)
解法:
算法思路:
01矩阵的变型题,直接用多源 bfs解决即可。
class Solution {
public:int dx[4] = {1, -1, 0, 0};int dy[4] = {0, 0, 1, -1};int maxDistance(vector<vector<int>>& grid) {int ret = -1;int m = grid.size(), n = grid[0].size();vector<vector<int>> dist(m, vector<int>(n, -1));queue<pair<int, int>> q;for(int i = 0; i < m; ++i)for(int j = 0; j < n; ++j)if(grid[i][j] == 1){q.push({i, j});dist[i][j] = 0;}while(q.size()){auto [a, b] = q.front(); q.pop();for(int k = 0; k < 4; ++k){int x = a + dx[k], y = b + dy[k];if(x >= 0 && x < m && y >= 0 && y < n && dist[x][y] == -1){q.push({x, y});dist[x][y] = dist[a][b] + 1;ret = max(ret, dist[x][y]);}}}return ret;}
};