小杰机器学习（six）——概率论——1.均匀分布2.正态分布3.数学期望4.方差5.标准差6.多维随机变量及其分布

1.均匀分布

连续概率分布中最简单的均匀分布

案例：

假设某站的公交车每10min来一趟，那么乘客候车时间X是(0,10),这个X就是服从均匀分布的随机变量。

均匀分布的高度是一致的也就每一份概率是相同的。

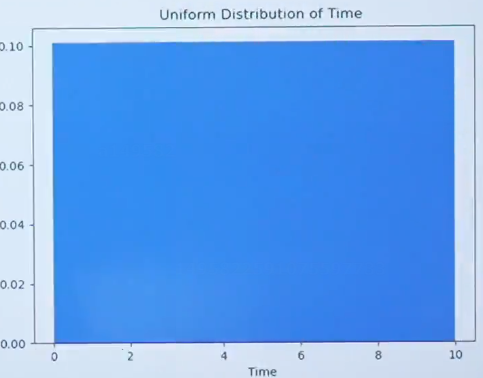
均匀分布的概率密度函数形式为：

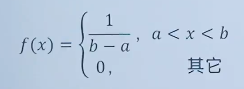
eg:pytorch中 w和b的初始化 就是基于均匀分布。

2.正态分布

正态分布和高斯分布其实是一个东西。

正态分布的引入

案例：在投硬币时，当投掷3次，“字”出现的次数会得到一个图像，如下所示：

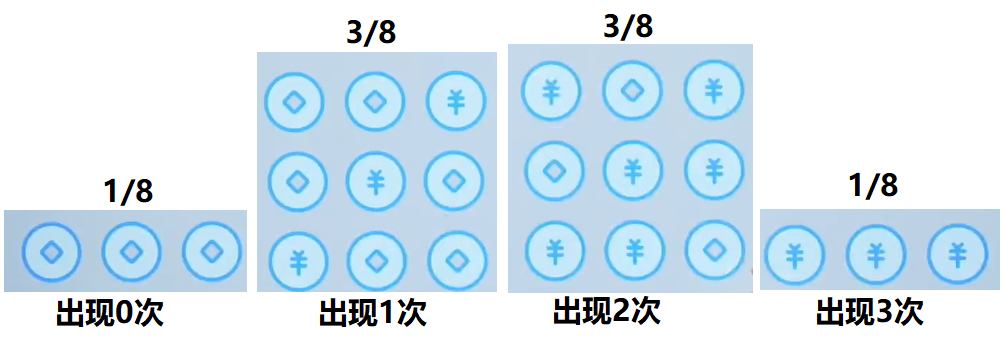
假设当投掷的次数变多之后，来看一下这个图示

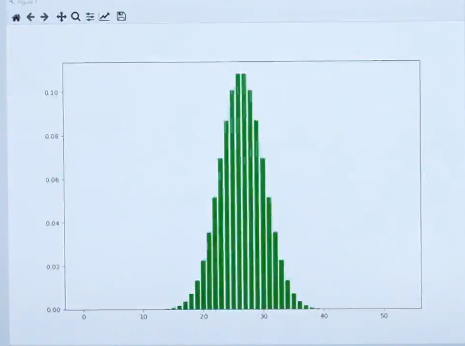
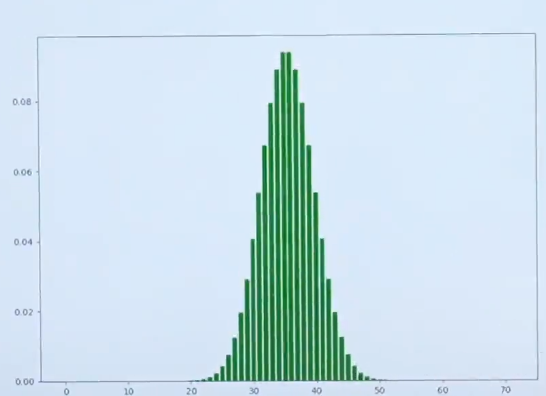
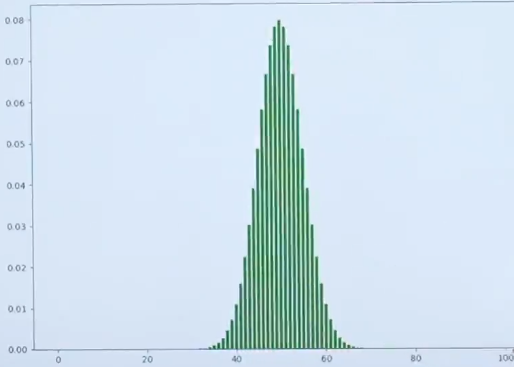
从图中可以观察到，不论是投掷50次还是100次，都类似于钟形图的图像。

形图远一点看，就可以把它看作一个曲线如下图所示。

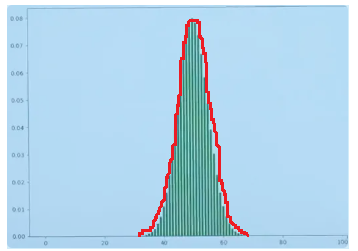
这个曲线就是正态分布。

刚才举的例子，离散的二项分布，当n特别大的时候，图像是接近于正态分布。

当前是从离散引入直观理解。

推导一下正态分布的公式：

目标使用钟形曲线拟合离散二项分布，获得正态分布的概率密度函数

案例：

在投硬币中，投掷4次硬币，“字”出现的次数会得到一个图像如下图所示，

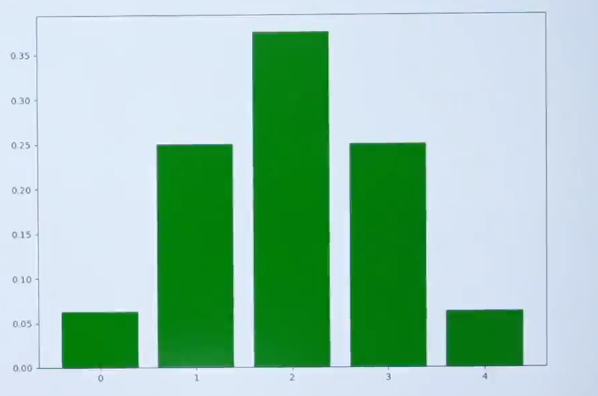
step1: 假设钟形图的公式为：

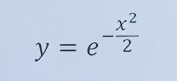
step2:对齐中心位置

画出钟形图如下所示

钟形图的中心在0位置，硬币分布的中心在2位置。硬币分布的中心2位置一般称为均值(μ)(后面会讲，这里先不讲)

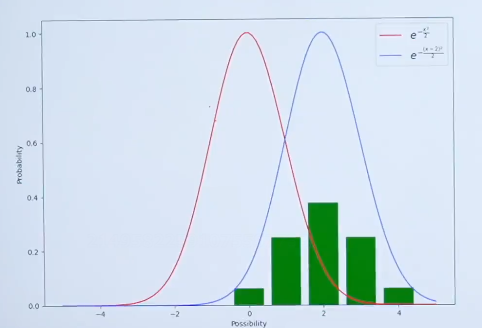
step3:调整钟形曲线的“陡峭”或“扁平”程度

钟形曲线的“陡峭”或“扁平”程度由标准差来决定。(标准差后面会讲)

经过计算当前蓝色曲线的标准差和硬币二项分布，标准差都是1。

下面演示一下标准差对 陡峭”或“扁平 ”的影响？

得出结论：

标准差决定曲线的“陡峭”或“扁平”程度：标准差越大，正态曲线越扁平；标准差越小，正态曲线越陡峭。

step4：面积相加和为1

钟形曲线经过均值和标准差调整后，最后一步就是调整钟形曲线的面积让其符合概率密度函数性质。

钟形曲线面积和硬币分布面积示意图

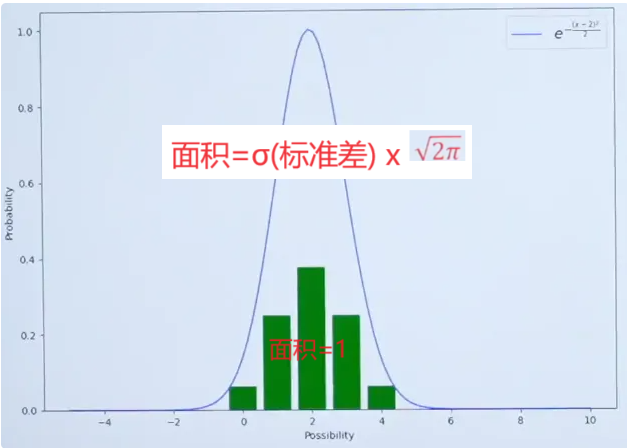
简单的思路就是计算出钟形曲线面积后，然后对其除以自身就得到了曲线面积和为1的值了，也就满足概率密度函数的性质了。

对于当前例子 σ=1 μ=2 面积归一化后的示意图如下图所示

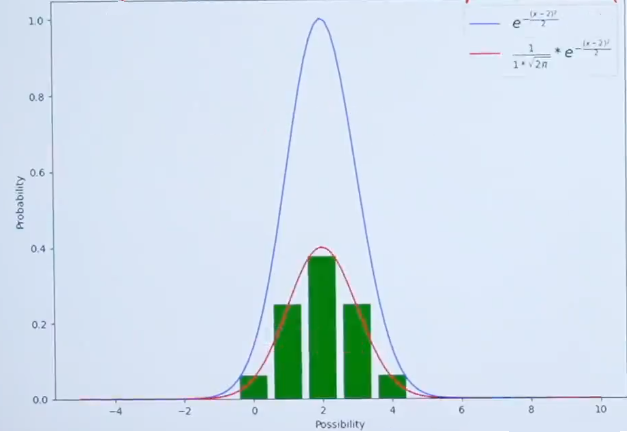
最后的正态分布的概率密度函数公式如下所示

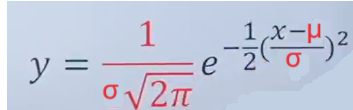
正态分布-总结

如果你有一个随机变量X，其概率密度函数为正态分布，可以写成这样。

均值：μ

标准差 ：σ

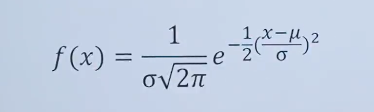
实际上都用下面的方式写：

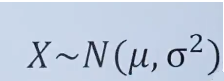
X是变量 N表示正态分布 ，μ均值 ，标准差的平方叫方差。有了均值和标准差后，正态分布就能求出来了

3.数学期望

数学期望其实和均值是画等号的

数学期望的引入：

期望是描述一个随机变量平均值的概念。对于离散型随机变量，期望E(X)的计算公式为：

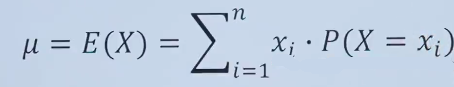
案例1：

与朋友打赌投硬币，每次需要6块钱本金，但如果“字”面朝上，那么就赢10块钱，否则本金不退回。

你是否会玩这个游戏？

在多次游戏中，有0.5的概率获得10元，有0.5的概率获得0元。

0.5*10+0.5*0=5->平均下来每次都能赢5元(数学期望) 本金是6块 5-6=-1 算下来之后其实是赔钱的。

本金6块，长远来看，并不能让你获利。

如果本金变成4块钱呢？在多次游戏中，有0.5的概率获得10元，有0.5的概率获得0元。

0.5*10+0.5*0=5 ->平均下来每次都能赢5元(数学期望) 本金4块 5-4=1 算下来之后其实是赚钱的。

本金4块，长远来看，能让你获利。

案例2：

考虑一个投掷一枚标准六面骰子的情况。随机变量X表示掷骰子的结果。计算骰子的期望：

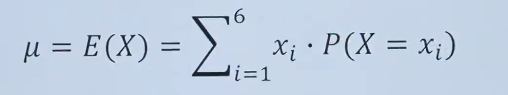
其中：

这意味着，如果你多次投掷六面骰子，预期每次的平均值接近3.5。

对于 1,2,3,4,5,6。3.5表示你有一半的几率投出来的是小的点也就是1,2,3。还有一半的几率是投出大的点是4,5,6。

函数的数学期望案例计算

假设有一个六面骰子，每个面的点数从1到6，用随机变量X表示投掷一次的结果。每次投掷完毕，获得投掷结果平方的金币，计算投掷一次骰子所获得金币的数学期望：

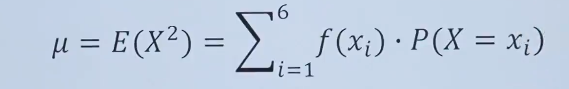
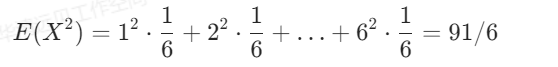
连续分布的数学期望数学表达：

离散的：

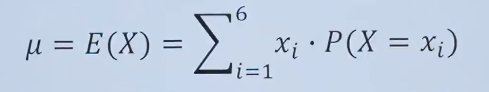
连续的：

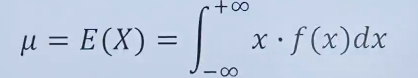
4.方差

方差是衡量随机变量分布离散程度的指标。对于离散型随机变量，方差Var(X)的计算公式为：

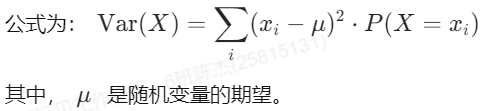
例子1：

与朋友打赌投硬币，但是如果“字”面朝上，那么就赢1块钱，否则就输1块钱，数学期望是多少？

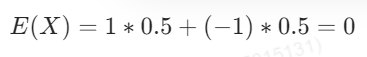
例子2：

与朋友打赌投硬币，但是如果“字”面朝上，那么就赢100块钱，否则就输100块钱，数学期望是多少？

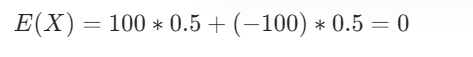
问：如果让你去玩的话，你感觉哪个风险更大？

直观上感觉第二个风险比较大！

那怎么用数学方法去量化这个风险？

如下图所示，将1 -1 ，100 -100画成了柱状图。

它们的概率都是0.5，两个例子的柱状图的均值是一样的，都是0位置。

但是两个柱状图的差值(也就是距离)是不一样的，差值其实是衡量风险量化的一个指标，

差值越大风险越大。

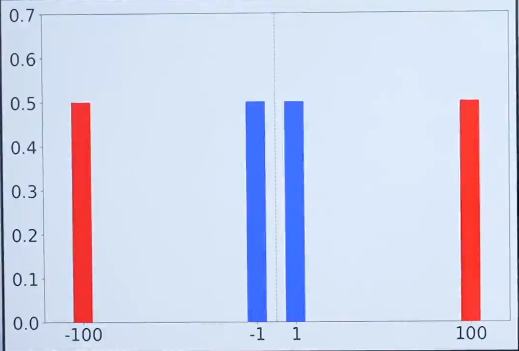
第一个案例

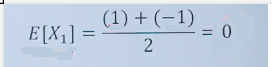
第二个案例

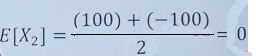
两个案例均值都是0。

为啥风险不一样但是计算出的风险感觉是一样呢，观察公式是不是都有正负号，正负抵消了。

如何消除抵消？

在线性回归里是不是已经提出方案了就是求平方。

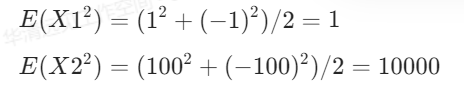
通过平方就真能，量化它的风险了？

案例3：

与朋友打赌投硬币，如果“字”面朝上，那么就赢得1块钱，否则输1块钱，数学期望是多少？

案例4：

与朋友打赌投硬币，但如果“字”面朝上，就赢4块钱，否则赢6块钱，数学期望是多少？

案例四的风险大。那画图看一下

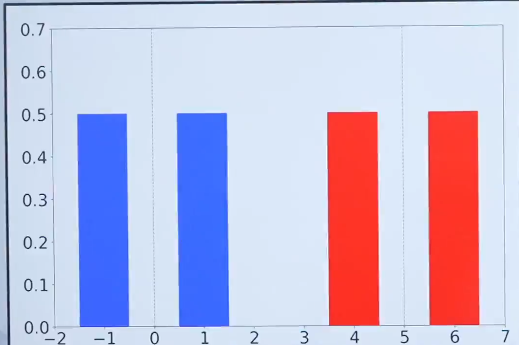
从图上看案例3和案例4的风险是一样的距离都是2

是不是就说明直接平方的方法需要优化改进？

图上看他们差值一样，但是没有对齐，直接让它们对齐后再比较。

对案例3：

案例3的均值μ=0

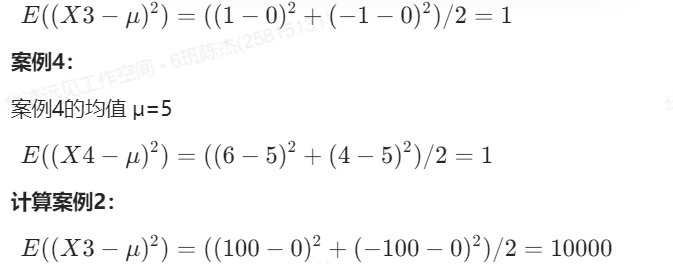
通过以上方案可以获得和数学上完全一致的一个内容，这个公式就叫方差

μ=E(X)

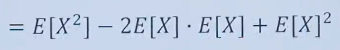
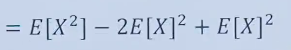
随机变量平方的期望减去数学期望的平方，方差的结果。

5.标准差

方差的特性：方差可以提供关于数据的离散程度的信息，但它的单位是数据单位的平方，这使得

它不太直观

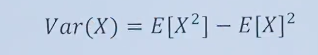
比如，身高的单位是m(米),但是使用方差计算离散程度单位是m*m，对于身高来讲，m*m显然是不对的。

怎么得到m(米)呢，直接开方就可以了

对方差开方从而得到数据单位：

上面公式得到的就是标准差，标准差用到的比较多，因为标准差的单位和随机变量X的单位是一致的。

正态分布：

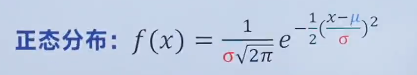
在正态分布中σ就是标准差。μ是数学期望或均值。

μ能实现它的平移

通过σ可以实现“陡峭”或“扁平”程度的调整

实现标准化分布

流程：

对数据进行中心化：将数据减去均值，使得数据的均值变为0

对数据进行缩放：将数据除以标准差，使得数据的标准差变为1.

可以通过一下公式实现：

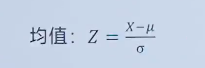
其中：Z是标准化后的数据。

X是原始数据

μ是原始数据的均值

σ是原始数据的标准差

方差和标准差的作用？

方差衡量的是每个数值与总体平均值的偏离程度的平方的平均数。

标准差是方差的平方根，它以原始数据单位来衡量数据的离散程度。

6.多维随机变量及其分布

这里不详细讲，对于机器学习和深度学习的学习了解一下就行。

多维随机变量是指由多个随机变量组成的向量，其取值可以使多维空间中的一个点。多维随机变量的

分布描述了这个向量的概率分布情况，即描述了各个随机变量之间以及它们与其他变量之间的关系。

联合分布描述了两个或多个随机变量同时取不同取值的概率情况。

多维正态分布：也称为多元正态分布，是最常见的多维分布之一。它具有与一维正态分布相似的性质，

但是描述了多个随机变量的联合分布情况。

多项分布：描述了多个类别的离散随机变量的分布，例如投掷一枚骰子多次的结果。

协方差矩阵：用于描述多维随机变量之间的相关性和方差的矩阵。