【入门算法】前缀和:先预存再求和,以空间换时间

半桔:个人主页
🔥 个人专栏: 《Linux手册》《手撕面试算法》《C++从入门到入土》
🔖人生忽如寄,莫辜负茶、汤、好天气。 -汪曾祺-
目录
前言
前缀和基础题目
303. 区域和检索 - 数组不可变
3427. 变长子数组求和
2559. 统计范围内的元音字符串数
3152. 特殊数组 II
1749. 任意子数组和的绝对值的最大值
3361. 两个字符串的切换距离
2055. 蜡烛之间的盘子
1744. 你能在你最喜欢的那天吃到你最喜欢的糖果吗?
53. 最大子数组和
总结
前言
有些题目需要统计一个连续子数组的长度,而每一个连续子数组都一定是整个数组的长度减去前面一部分和后面一部分,也可以表示为两个前缀和的差。
所以在处理这种连续子数组的和时,如果直接使用暴力需要O(N)才能计算出和,但是如果提前计算出到达所有位置的前缀和,就可以使用O(1)的时间得到连续数组的和。
PS:本篇博客中的所有题目均来自于灵茶山艾府 - 力扣(LeetCode)分享的题单
前缀和基础题目
303. 区域和检索 - 数组不可变

此题就是经典的连续数组和问题,可以使用前缀和计算出到达每个位置时,前面所有数据的总和。
这样计算[left,right]的时候就可以直接使用 lsum[right] - lsum[left-1];
细节:上面在进行相减的时候,left-1可能会越界,所以可以特判一下;或者将前缀和数组整体先后移动一个单位,即6下标记录[0,5]元素的和,这样就不会导致越界了,lsum[right+1] - lsum[left];
class NumArray {vector<int> lsum; //记录从左向右到每个位置的和
public:NumArray(vector<int>& nums) {int n = nums.size();lsum.resize(n+1);for(int i = 0;i < n ;i++)lsum[i+1] = lsum[i] + nums[i]; //记录前缀和}int sumRange(int left, int right) {return lsum[right+1] - lsum[left];}
};/*** Your NumArray object will be instantiated and called as such:* NumArray* obj = new NumArray(nums);* int param_1 = obj->sumRange(left,right);*/3427. 变长子数组求和


依旧要求子数组的和,只不过此题需要求多个子数组的和,其中子数组为[start,i]一共有n个。
可以一边补充前缀和数组,一边将以i为结尾的子数组和添加到答案中。
class Solution {
public:int subarraySum(vector<int>& nums) {int n = nums.size(),ret = 0;vector<int> lsum(n+1);for(int i = 0; i < n;i++){lsum[i+1] = lsum[i] + nums[i]; //计算前缀和int start = max(0,i - nums[i]); //查找起始位置ret += lsum[i+1] - lsum[start]; //添加答案} return ret;}
};2559. 统计范围内的元音字符串数

此题不再是统计子数组的和了,而是统计一定范围内字符串以元音开始和结束的个数。
但是道理都一样,还是通过前缀和的方式来解决。
class Solution {
public:vector<int> vowelStrings(vector<string>& words, vector<vector<int>>& queries) {//此题不再是统计子数组的和了,而是统计一定范围内字符串以元音开始和结束的个数int n = words.size(),m = queries.size();unordered_set<char> s({'a','e','i','o','u'});vector<int> lsum(n+1);for(int i = 0; i < n;i++)lsum[i+1] = lsum[i] + (s.count(words[i][0])&&s.count(words[i].back()));vector<int> ret(m);for(int i = 0 ;i < m;i++)ret[i] = lsum[queries[i][1]+1] - lsum[queries[i][0]];return ret;}
};3152. 特殊数组 II

此题是对子数组进行判断,判断子数组是否满足特殊数组的条件。
如果直接暴力求解,O(N^2)超时,需要进行优化;
可以统计到达每个位置是该位置可以与前面组成的特殊数组的长度;
这样在检查一个区间[start,end]的时候,直接检查(end位置组成的特殊数组的长度-start位置组成的特殊数组的长度)是否等于(end-start)即可。
class Solution {
public:vector<bool> isArraySpecial(vector<int>& nums, vector<vector<int>>& queries) {//此题是对子数组进行判断,判断子数组是否满足特殊数组的条件//如果直接暴力求解,O(N^2)超时,需要进行优化//可以统计到达每个位置是该位置可以与前面组成的特殊数组的长度;//这样在检查一个区间[start,end]的时候,直接检查(end位置组成的特殊数组的长度-start位置组成的特殊数组的长度)是否等于(end-start)即可int n = nums.size(),m = queries.size();vector<int> lsum(n);lsum[0] = 1;for(int i = 1; i < n;i++){int clo = nums[i]%2 + nums[i-1]%2; //判断是时不时奇偶相邻,如果是clo为1if(clo==1) lsum[i] = lsum[i-1] + 1; //紧接着上一个继续计数else lsum[i] = 1; //重新开始计数}vector<bool> ret(m);for(int i = 0 ;i < m; i++){int start = queries[i][0],end = queries[i][1];ret[i] = (end-start == lsum[end] - lsum[start]); //判断子数组中间部分奇偶是不是连续的}return ret;}
};1749. 任意子数组和的绝对值的最大值

求一个区间的绝对值可以使用abs(lsum[end]-sum[start]);
求出每个区间的绝对值后如何求出最大的呢???;
最大绝对值 = 最大和 - 最小和。
class Solution {
public:int maxAbsoluteSum(vector<int>& nums) {//求一个区间的绝对值可以使用abs(lsum[end]-sum[start])//求出每个区间的绝对值后如何求出最大的呢???//最大绝对值 = 最大和 - 最小和int n = nums.size(),low = 0 ,heig = 0; //使用low记录最小和在,heig记录最大和vector<int> lsum(n+1);for(int i = 0 ; i < n;i++){lsum[i+1] = lsum[i] + nums[i]; //更新前缀和low = min(low,lsum[i+1]); //更新最大值和最小值heig = max(heig,lsum[i+1]);}return heig - low;}
};3361. 两个字符串的切换距离


在进行转变的时候我们需要知道从一个字符到另一个字符需要的代价是多少;
题目中已知的是每个字符转换的代价,所以可以使用前缀和得到从一个字符到另一个字符的代价;
比较从前往后和从后往前到达目标位置哪一个花费更少,
细节:注意边界问题分析。
class Solution {typedef long long LL;
public:long long shiftDistance(string s, string t, vector<int>& nextCost, vector<int>& previousCost) {//在进行转变的时候我们需要知道从一个字符到另一个字符需要的代价是多少//题目中已知的是每个字符转换的代价,所以可以使用前缀和得到从一个字符到另一个字符的代价vector<LL> lsum(27); //i位置表示从a到i+'a'的代价vector<LL> rsum(27); //i位置表示从z到'a'+i-1的代价for(int i = 0 ;i < 26 ;i++){lsum[i+1] = lsum[i] + nextCost[i];rsum[25-i] = rsum[26-i] + previousCost[25-i];}//开始进行转换LL ret = 0;for(int i = 0 ;i <s.size(); i++){if(s[i] == t[i]) continue;LL next, prev ;if(s[i] < t[i]) //t[i]在后面{next = lsum[t[i]-'a'] - lsum[s[i]-'a'];prev = rsum[0] - rsum[s[i]-'a'+1] + rsum[t[i]-'a'+1];}else //t[i]在前面{next = lsum[26] - lsum[s[i]-'a'] + lsum[t[i]-'a'];prev = rsum[t[i]-'a'+1] - rsum[s[i]-'a'+1];}ret += min(next,prev);}return ret;}
};2055. 蜡烛之间的盘子

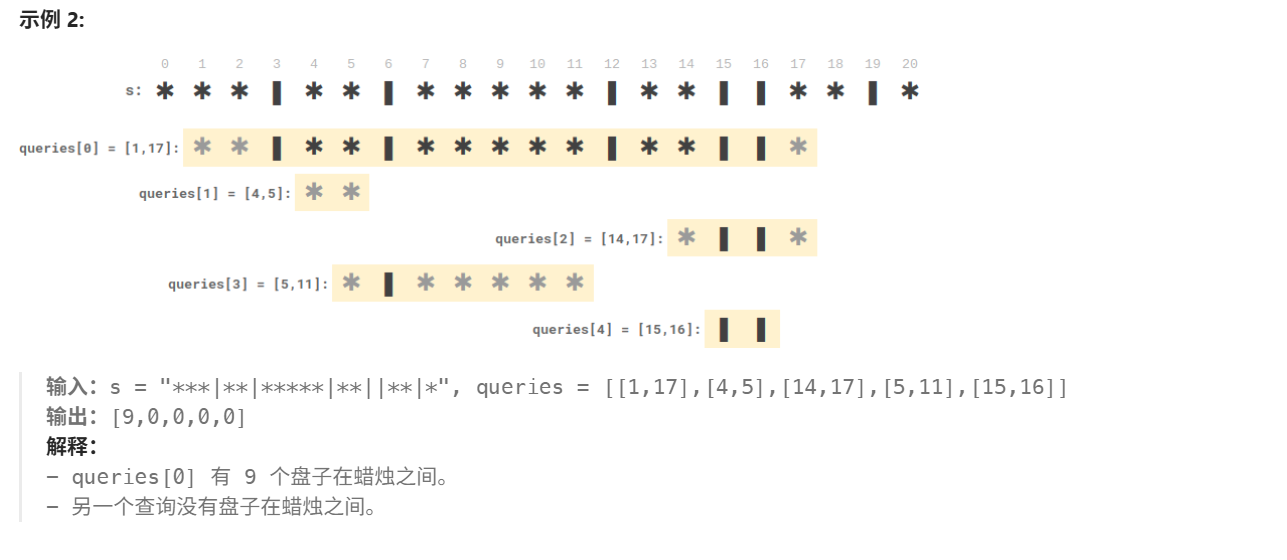
根据题意要确定一个区间中蜡烛的个数就需要确定:区间中最外侧盘子的位置,盘子内部蜡烛的个数
所以需要使用三个前缀和来解决:
记录从前往后到i位置前面最近的位置位置;记录从后往前到i位置后面最近的盘子位置;
记录从前往后到i位置蜡烛的个数。
class Solution {
public:vector<int> platesBetweenCandles(string s, vector<vector<int>>& queries) {//根据题意要确定一个区间中蜡烛的个数就需要确定:区间中最外侧盘子的位置,盘子内部蜡烛的个数//所以需要使用三个前缀和来解决.//记录从前往后到i位置前面最近的位置位置;记录从后往前到i位置后面最近的盘子位置//记录从前往后到i位置蜡烛的个数int n = s.size(),m=queries.size();vector<int> prev(n,-1),back(n,-1),count(n); //三个前缀和if(s[0] == '|') prev[0] = 0,count[0] = 1;if(s[n-1] == '|') back[n-1] = n-1; for(int i = 1;i < n;i++){if(s[i] == '*' ) prev[i] = prev[i-1];else prev[i] = i;if(s[n-1-i]=='*') back[n-1-i] = back[n-i];else back[n-1-i] = n-1-i;count[i] += count[i-1] + (s[i]=='*'); //记录蜡烛个数}vector<int> ret(m);for(int i = 0;i < m;i++){int a = queries[i][0],b = queries[i][1];int end = prev[b],start = back[a]; //最近盘子的位置int num = 0;if(end != -1&&start != -1&&end > start + 1) num = count[end-1]-count[start]; //盘子之间蜡烛的个数ret[i] = num;}return ret;}
};1744. 你能在你最喜欢的那天吃到你最喜欢的糖果吗?


题目很长,但是理解后题目就很简单;
题目要求我们判断是否能在favoriteDayi吃到favoriteTypei糖,每天至少吃1颗糖,最多吃dailyCapi颗
吃糖的顺序必须是从下标0位置依次往后;
所以使用前缀和来统计每种糖前面有多少颗糖
细节:一天可以吃两种糖,所以在favoriteDayi也可以先吃前一种糖,所以(day+1)*cap > lsum[type]即可,还要保证每天吃一颗糖的情况下不会把favoriteTypei糖吃完,所有就是day < lsum[type+1]。
class Solution {typedef long long LL;
public:vector<bool> canEat(vector<int>& candiesCount, vector<vector<int>>& queries) {//题目很长,但是理解后题目就很简单、//题目要求我们判断是否能在favoriteDayi吃到favoriteTypei糖,每天至少吃1颗糖,最多吃dailyCapi颗//吃糖的顺序必须是从下标0位置依次往后//所以使用前缀和来统计每种糖前面有多少颗糖int n = candiesCount.size(),m = queries.size();vector<LL> lsum(n+1);for(int i = 0;i < n;i++)lsum[i+1] = lsum[i] + candiesCount[i];vector<bool> ret;for(auto& nums: queries){LL type = nums[0] ,day = nums[1] ,cap = nums[2];if((day+1)*cap > lsum[type] && day < lsum[type+1]) ret.push_back(true);else ret.push_back(false);}return ret;}
};53. 最大子数组和

连续子数组的和,考虑前缀和;
当遍历到第i个位置的时候,在前面找最小前缀和,将i位置的前缀和-最小前缀和就可以得到[0,i]位置中最大子数组,枚举每一个i选取所以[0,i]中子数组的最大值,就是题目中要求的[0,n-1]子数组中的最大值。
class Solution {
public:int maxSubArray(vector<int>& nums) {//连续子数组的和//当遍历到第i个位置的时候,在前面找最小前缀和,将i位置的前缀和-最小前缀和就可以得到[0,i]位置中最大子数组int n = nums.size(),prev = 0 ,ret=INT_MIN;vector<int> lsum(n+1);for(int i = 0; i < n;i++){lsum[i+1] = lsum[i] + nums[i]; //存储前缀和最大值ret = max(ret,lsum[i+1]-prev); //更新答案prev = min(prev,lsum[i+1]); //更新前缀和最小值}return ret;}
};总结
一般题目中出现要求一个区间的....的时候,就可以考虑前缀和来解决,尤其是对于子数组的和。
