当前位置：首页 > news >正文

论文解读——矩形隧道中MIMO信道特性的模态理论解释

news 2025/9/22 6:46:33

矩形隧道中MIMO信道特性的模态理论解释

J. M. Molina-Garcia-Pardo, M. Lienard, P. Degauque, D. G. Dudley and L. Juan-Llacer, “Interpretation of MIMO Channel Characteristics in Rectangular Tunnels From Modal Theory,” in IEEE Transactions on Vehicular Technology, vol. 57, no. 3, pp. 1974-1979, May 2008, doi: 10.1109/TVT.2007.913177.

摘要

本文开发了一种用于分析具有损耗壁的矩形隧道中多输入多输出（MIMO）无线信道传播的模态方法。通过参数化方法深入研究了模式数量和天线间距离对系统性能的影响。我们以信道容量为性能指标，详细评估了MIMO信道作为距离和隧道尺寸函数的表现。研究表明，在隧道环境中，模式的准正交性、有效模式数量的衰减以及空间相关性是影响MIMO系统性能的关键因素。

1. 引言

本文基于Foschini-Telatar信息理论的突破性成果，该理论预测MIMO信道相比香农单信道容量可实现显著的容量提升。在隧道这一特殊环境中，电磁波传播可以用具有损耗壁的波导中的模式来精确建模。这种建模方法最初在20世纪70年代为矿井通信所开发，后来被Mahmoud系统化地总结在其著作中。

Loyka最近提出，个别波导模式可以作为MIMO传播信道，他的重点是完全导电壁的波导，其中模式是相互正交的。本文将这项工作扩展到具有损耗壁的超尺寸引导结构的情况。我们的研究动机来自Liénard等人在巴黎地铁隧道中进行的MIMO实验项目。实验发现，即使假设信噪比（SNR）恒定，信道容量也是纵向距离的递减函数。这可能由两种现象造成：首先，在大距离处，包含接收天线的横向平面中主导模式的数量可能变得小于发射或接收元件的数量，导致传输矩阵退化，如果只有一个模式占主导地位，则会出现所谓的"钥匙孔"效应。其次，接收阵列元件之间的相关性随距离增加，当模式数量非常大时才能获得小的相关性。另一方面，必须强调的是，容量也与发射元件之间的相关性密切相关，即两个阵列元件激发的模式集之间的相关性。

2. 隧道传播的模态理论

2.1 模式正交性与自伴算子

模式正交性的数学基础源于微分算子的谱理论。对于具有圆形横截面和完全导电边界壁的理想波导，横截面本征函数由以下两个微分算子决定：

角向算子：具有周期边界条件的二阶微分算子
$1r∂∂ϕ(r∂Ψ∂ϕ)+kϕ2Ψ=0\frac{1}{r}\frac{\partial}{\partial \phi}\left(r\frac{\partial \Psi}{\partial \phi}\right) + k_\phi^2\Psi = 0$
边界条件： $Ψ(ϕ)=Ψ(ϕ+2π)\Psi(\phi) = \Psi(\phi + 2\pi)$
径向贝塞尔算子：在边界壁处具有狄利克雷或诺伊曼边界条件
$d2Rdr2+1rdRdr+(k2−n2r2)R=0\frac{d^2R}{dr^2} + \frac{1}{r}\frac{dR}{dr} + \left(k^2 - \frac{n^2}{r^2}\right)R = 0$
边界条件： $R (a) = 0$ （狄利克雷）或 $dRdr∣r=a=0\frac{dR}{dr}\bigg|_{r=a} = 0$ （诺伊曼）

这两个算子都是自伴的，产生的本征函数满足正交关系。然而，当波导变成由损耗介质包围的圆柱形隧道时，情况发生根本性变化。虽然角算子仍保持周期边界条件，因此角本征函数保持正交性，但径向本征函数失去了严格的正交性质。

对于被损耗介质包围的矩形隧道，正交条件进一步退化，主要原因包括：

微分算子不再是自伴的，模态函数的正交性特征消失，导致模式耦合的可能性
由于边界不沿完整的坐标面出现，不再可能精确求解边值问题，需要开发近似方法

2.2 矩形隧道中的模态展开

考虑沿 $z$ 轴的矩形隧道，横截面尺寸为 $(x, y) = (a, b)$ 。坐标原点位于横截面中心， $z = 0$ 定义激励平面。对于 $y$ 向（垂直）偶极子激励，该结构支持的自然模式是指数为 $(m, n)$ 的 $y$ 向混合模式 $EH_{m,n}$ 。

电场的完整模态展开为：
$\sum_{m=0}^{\infty}\sum_{n=0}^{\infty}\alpha_{m,n}(z)e_{m,n}(x, y)$

其中模态本征函数 $e_{m,n}(x,y)$ 满足亥姆霍兹方程：
$∇t2em,n+kt2em,n=0\nabla_t^2 e_{m,n} + k_t^2 e_{m,n} = 0$

这里 $∇t2=∂2∂x2+∂2∂y2\nabla_t^2 = \frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2}$ 是横向拉普拉斯算子， $k_t$ 是横向波数。

模态系数的空间演化由传播因子决定：
$αm,n(z)=βm,ne−jkm,nz\alpha_{m,n}(z) = \beta_{m,n}e^{-jk_{m,n}z}$

其中 $βm,n\beta_{m,n}$ 是在激励平面 $(z = 0)$ 处确定的复振幅， $k_{m,n}$ 是第 $(m, n)$ 个模式的传播常数：
$km,n=k02εr−kt,mn2k_{m,n} = \sqrt{k_0^2\varepsilon_r - k_{t,mn}^2}$

这里 $k0=2π/λ0k_0 = 2\pi/\lambda_0$ 是自由空间波数， $εr\varepsilon_r$ 是隧道壁的相对介电常数。

2.3 模式耦合分析

模式耦合因子定量描述了模式偏离正交性的程度：
$ρm,n,m′,n′=∫−a/2a/2∫−b/2b/2em,n(x,y)em′,n′∗(x,y)dxdy\rho_{m,n,m',n'} = \int_{-a/2}^{a/2}\int_{-b/2}^{b/2}e_{m,n}(x,y)e^*_{m',n'}(x,y)dxdy$

对于完全导电壁，该因子严格满足：
$ρm,n,m′,n′=δm,m′δn,n′\rho_{m,n,m',n'} = \delta_{m,m'}\delta_{n,n'}$

而对于损耗壁，需要考虑复数传播常数和本征函数的影响。

表I：归一化模式的正交性（8×4.5米隧道）

模式阶数 $e_{m,n}$	$max⁡(∣ρ∣)\max(\|\rho\|)$
5,4	0.0046
8,5	0.0084
10,6	0.0133
15,7	0.0195
20,8	0.0272
25,9	0.0363
30,10	0.0471

表I显示，即使对于高阶模式（如 $m = 30, n = 10$ 的60个模式），模式耦合因子的最大值仅为 $10^{-2}$ 量级，而前九个模式之间的耦合因子小于 $\times 10^{-3}$ 。这证实了准正交性假设的有效性。

2.4 模式系数的确定

通过傅里叶变换技术确定模式系数：
$αm,n(z)=1Nm,n∫−a/2a/2∫−b/2b/2E(x,y,z)em,n(x,y)dxdy\alpha_{m,n}(z) = \frac{1}{N_{m,n}}\int_{-a/2}^{a/2}\int_{-b/2}^{b/2}E(x,y,z)e_{m,n}(x,y)dxdy$

其中归一化因子：
$Nm,n=∫−a/2a/2∫−b/2b/2∣em,n(x,y)∣2dxdyN_{m,n} = \int_{-a/2}^{a/2}\int_{-b/2}^{b/2}|e_{m,n}(x,y)|^2dxdy$

在实际计算中，我们使用射线理论来计算场 $E (x, y, z)$ ，这种方法在文献中已被广泛验证和使用。

3. 有效模式数分析

3.1 发射机位置的影响

发射天线的位置对激发的模式谱有决定性影响。对于单输入单输出（SISO）系统，中心位置的天线主要激发最低阶模式 $EH_{11}$ ，该模式具有最小的衰减。然而，对于MIMO系统，研究表明当每个发射阵列元件激发的模式数量增加时，容量会提高。

当发射元件偏离中心时，会以几乎相似的权重激发大量模式。数值计算表明，在大隧道中600米距离处，对于偏移到隧道宽度1/4的天线，有五个模式的相对振幅（归一化到 $EH_{11}$ 模式）大于-7 dB，而中心源仅有三个。

3.2 有效模式数的定义与计算

定义有效模式数 $N_a(x\%)$ 为功率至少等于最强模式功率 $x%x\%$ 的模式数量：
$Na(x%)=∑m,nH(∣Am,n∣2∣Amax∣2−x100)N_a(x\%) = \sum_{m,n} H\left(\frac{|A_{m,n}|^2}{|A_{max}|^2} - \frac{x}{100}\right)$

其中 $H(⋅)H(\cdot)$ 是Heaviside阶跃函数， $A_{m,n}$ 是模式振幅， $A_{max}$ 是最大模式振幅。

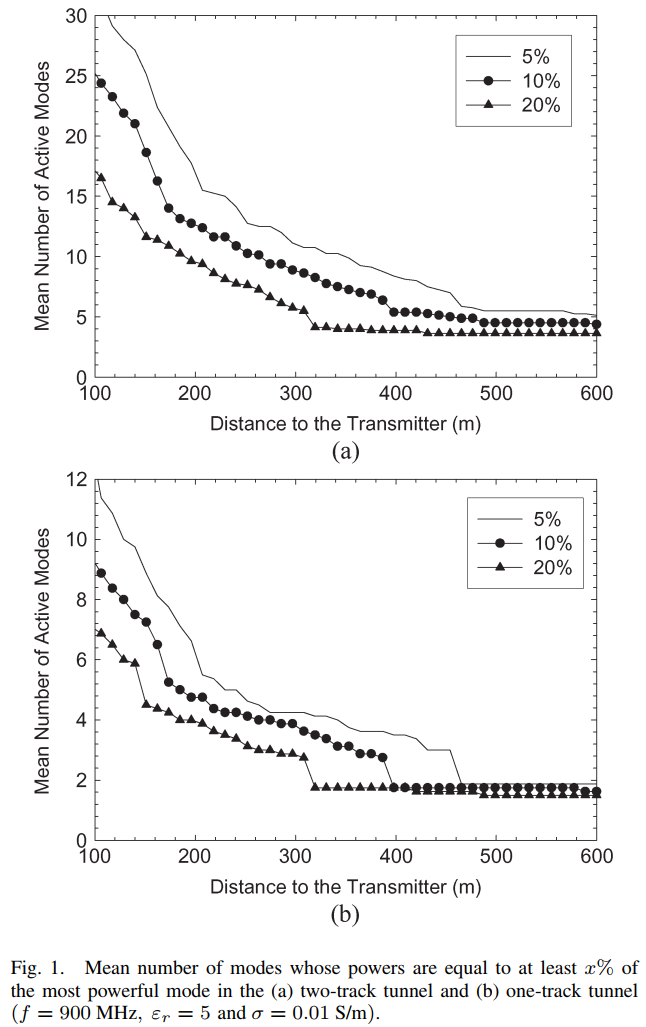
图1描述：图1展示了两种隧道中有效模式数随距离的变化。图(a)显示了8×4.5米双轨隧道的结果，图(b)显示了4×4.5米单轨隧道的结果。三条曲线分别对应5%、10%和20%的功率阈值。可以观察到：

有效模式数随距离单调递减
大隧道中的有效模式数显著高于小隧道
在100米处，20%阈值下大隧道约有25个有效模式，而小隧道仅有12个
在600米处，两种隧道的有效模式数都趋于稳定，大隧道约5个，小隧道约2个

4. 接收端空间相关性

4.1 横向相关函数

接收阵列元件之间的空间相关性是影响MIMO性能的关键因素。对于位于 $(x, y, z)$ 和 $(x+Δx,y,z)(x+\Delta x,y,z)$ 的两个接收点，相关系数定义为：
$ρrx(Δx,z)=⟨E(x,y,z)E∗(x+Δx,y,z)⟩⟨∣E(x,y,z)∣2⟩⟨∣E(x+Δx,y,z)∣2⟩\rho_{rx}(\Delta x, z) = \frac{\langle E(x,y,z)E^*(x+\Delta x,y,z)\rangle}{\sqrt{\langle|E(x,y,z)|^2\rangle\langle|E(x+\Delta x,y,z)|^2\rangle}}$

其中 $⟨⋅⟩\langle\cdot\rangle$ 表示对横向位置的系综平均。

4.2 相关距离的物理机制

相关距离随轴向距离增加的物理机制可以理解为：在近场区域，大量模式之间的干涉产生快速的场变化，导致小的相关距离。随着传播距离增加，高阶模式逐渐衰减，剩余模式之间的干涉图样变得更加平滑，导致相关距离增加。

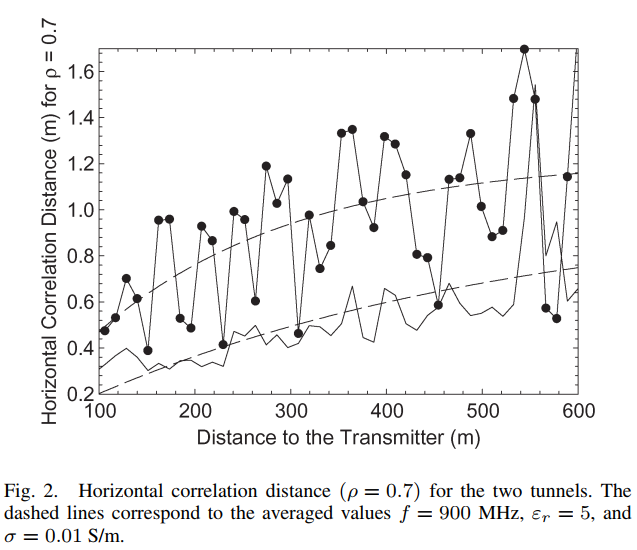
图2描述：图2展示了使 $ρ=0.7\rho = 0.7$ 的水平相关距离随传输距离的变化。实线表示8×4.5米隧道，虚线表示4×4.5米隧道。主要特征包括：

相关距离呈现高度波动的特性，反映了模式干涉的复杂性
总体趋势是相关距离随传输距离增加
大隧道的相关距离普遍小于小隧道
在100-200米范围内，相关距离约为0.4-0.8米
在500-600米处，相关距离可达1.6米

5. 发射端相关性

5.1 模式激发的相关性

元件 $j_1$ 和 $j_2$ 激发的模式之间的相关性通过以下相关矩阵定义：
$Rα(j1,j2)=1MN∑m∑n(αm,n(z,j1)−⟨αm,n(z,j1)⟩)×(αm,n∗(z,j2)−⟨αm,n∗(z,j2)⟩)R_\alpha(j_1, j_2) = \frac{1}{MN}\sum_m\sum_n(\alpha_{m,n}(z,j_1) - \langle\alpha_{m,n}(z,j_1)\rangle) \times (\alpha^*_{m,n}(z,j_2) - \langle\alpha^*_{m,n}(z,j_2)\rangle)$

归一化相关系数为：
$ρj1j2α(z)=∣Rα(j1,j2)∣[Rα(j1,j1)Rα(j2,j2)]1/2\rho^\alpha_{j_1j_2}(z) = \frac{|R_\alpha(j_1,j_2)|}{[R_\alpha(j_1,j_1)R_\alpha(j_2,j_2)]^{1/2}}$

5.2 电场相关性

发射元件产生的电场之间的相关性 $ρj1j2E(z)\rho^E_{j_1j_2}(z)$ 不同于模式相关性 $ρj1j2α(z)\rho^\alpha_{j_1j_2}(z)$ ，因为它考虑了模式之间的拍频或干涉：
$ρj1j2E(z)=∣RE(j1,j2)∣[RE(j1,j1)RE(j2,j2)]1/2\rho^E_{j_1j_2}(z) = \frac{|R_E(j_1,j_2)|}{[R_E(j_1,j_1)R_E(j_2,j_2)]^{1/2}}$

其中：
$RE(j1,j2)=1MN∑m∑n(αm,n(z,j1)−⟨αm,n(z,j1)⟩)×(αm,n∗(z,j2)−⟨αm,n∗(z,j2)⟩)×(αm,n∗(z,j2)−⟨αm,n∗(z,j2)⟩)R_E(j_1,j_2) = \frac{1}{MN}\sum_m\sum_n(\alpha_{m,n}(z,j_1) - \langle\alpha_{m,n}(z,j_1)\rangle) \times (\alpha^*_{m,n}(z,j_2) - \langle\alpha^*_{m,n}(z,j_2)\rangle) \times \left(\alpha^*_{m,n}(z,j_2) - \langle\alpha^*_{m,n}(z,j_2)\rangle\right)$

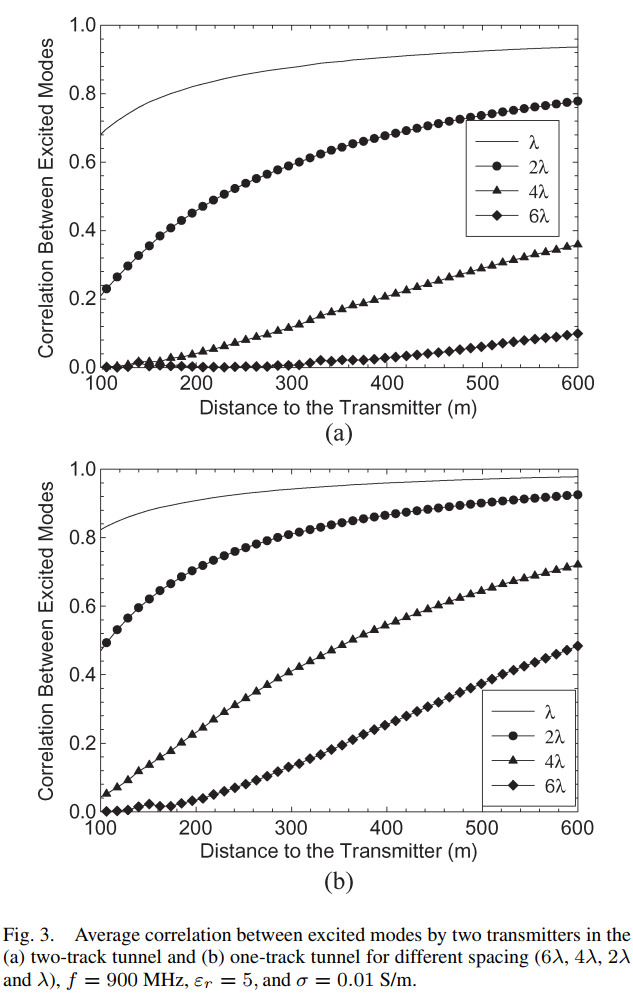
图3描述：图3展示了两个隧道中激发模式之间的平均相关性。图(a)为8×4.5米隧道，图(b)为4×4.5米隧道。四条曲线分别对应λ、2λ、4λ和6λ的天线间距。关键观察包括：

相关性随距离单调增加
天线间距越大，相关性越低
小隧道中的相关性增长更快
对于2λ间距，大隧道在430米处达到0.7相关性，小隧道在190米处达到

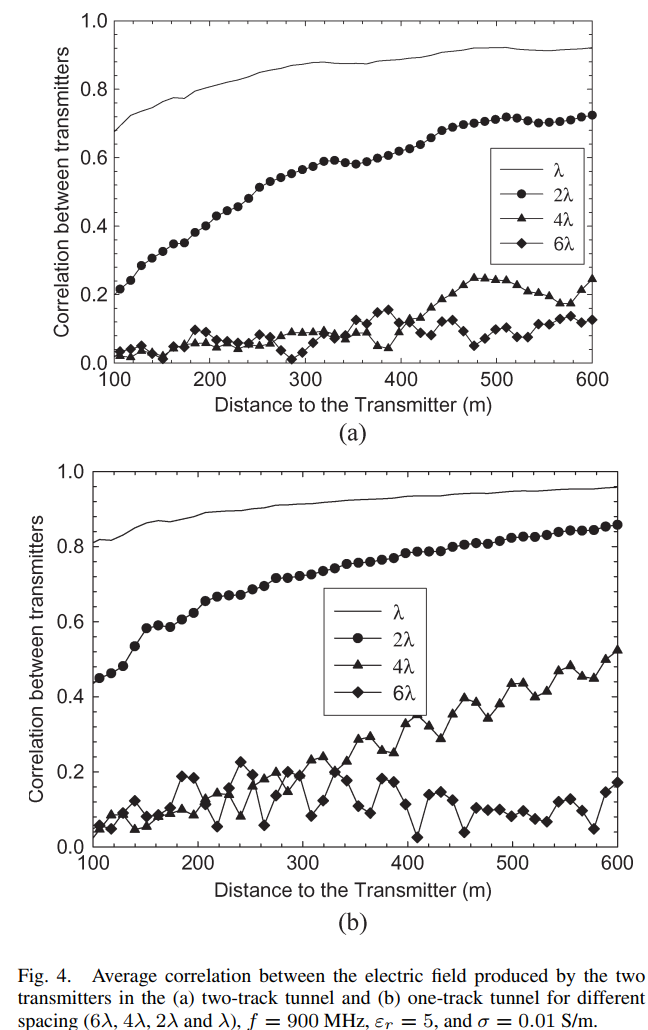
图4描述：图4展示了两个发射机产生的电场之间的平均相关性。与图3相比，电场相关性考虑了模式间的干涉效应。主要特点：

相关性曲线呈现更大的波动
总体趋势与模式相关性相似
在某些距离处出现局部最小值，这是由于模式间的相消干涉
对于2λ间距，大隧道在470米处达到0.7相关性，小隧道在260米处达到

6. MIMO信道容量

6.1 信道模型

对于 $\times N$ MIMO系统，接收信号向量为：
$y=Hx+n\mathbf{y} = \mathbf{H}\mathbf{x} + \mathbf{n}$

其中 $x\mathbf{x}$ 是 $\times 1$ 发射向量， $n\mathbf{n}$ 是 $\times 1$ 加性高斯白噪声向量，噪声协方差矩阵为 $Rn=σn2IN\mathbf{R}_n = \sigma_n^2\mathbf{I}_N$ 。

6.2 传输矩阵的构建

传输矩阵 $H\mathbf{H}$ 的每个元素由模态展开给出：
$hij(z)=∑m∑nαm,nj(z)em,n(xi,yi)h_{ij}(z) = \sum_m\sum_n\alpha^j_{m,n}(z)e_{m,n}(x_i,y_i)$

为了进行公平比较，我们使用Frobenius范数对矩阵进行归一化：
$Hnorm=H1100NM∑k=1100∑i=1N∑j=1M∣(hij)k∣2\mathbf{H}_{norm} = \frac{\mathbf{H}}{\sqrt{\frac{1}{100NM}\sum_{k=1}^{100}\sum_{i=1}^{N}\sum_{j=1}^{M}|(h_{ij})_k|^2}}$

6.3 信道容量计算

瞬时信道容量为：
$\log_2\left(\det\left(\mathbf{I}_N + \frac{SNR}{M}\mathbf{H}\mathbf{H}^\dagger\right)\right) \text{ bits/s/Hz}$

对于高SNR情况，容量可以近似为：
$\approx \min(M,N)\log_2(SNR) + \log_2(\det(\mathbf{H}\mathbf{H}^\dagger))$

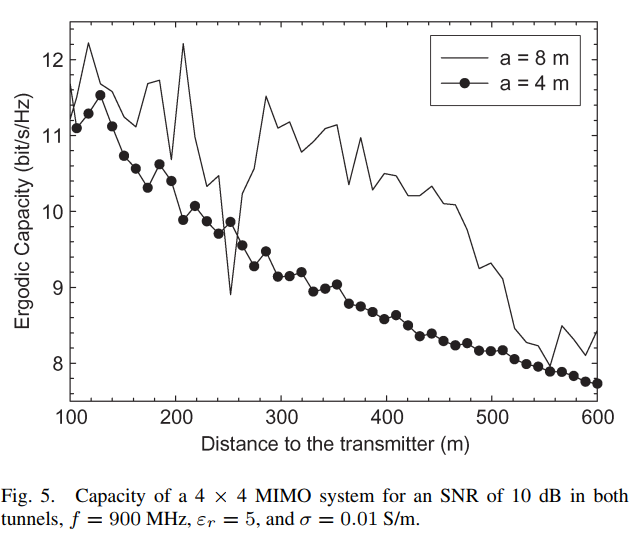
图5描述：图5展示了SNR = 10 dB时4×4 MIMO系统的容量。实线表示8×4.5米隧道，虚线表示4×4.5米隧道。主要观察结果：

大隧道的容量在100-450米范围内保持相对稳定（10-11 bits/s/Hz）
小隧道的容量从100米开始单调递减
100米处两隧道容量相近，约为独立瑞利信道容量（13.8 bits/s/Hz）的80%
600米处，大隧道容量约8 bits/s/Hz，小隧道约7.5 bits/s/Hz
相比SISO系统（3 bits/s/Hz），MIMO系统仍有显著增益

7. 结论

本文通过模态理论方法系统分析了矩形隧道中MIMO信道的传播特性。主要贡献和发现包括：

准正交性验证：尽管损耗壁破坏了严格的模式正交性，但模式耦合因子保持在 $10^{-2}$ 量级以下，验证了准正交假设的有效性。
有效模式数的影响：有效模式数随距离快速衰减，特别是在小隧道中。这限制了空间复用增益的实现范围。
空间相关性的双重作用：接收端和发射端的空间相关性共同决定了MIMO系统的性能极限。相关距离随传播距离增加，要求更大的天线间距。
容量性能评估：即使在不利条件下，4×4 MIMO系统相比SISO系统仍能提供显著的容量增益。在合理的传输距离内（大隧道500米，小隧道350米），可实现3倍以上的容量提升。
实际应用指导：
- 大隧道（8×4.5米）中，MIMO系统可在500米范围内有效工作
- 小隧道（4×4.5米）中，有效范围约为200-300米
- 天线间距应至少为2λ以保证足够低的相关性
- 发射天线偏离中心放置可激发更多模式，提高系统容量

附录A：模态本征函数的推导

A.1 亥姆霍兹方程的分离变量解

在矩形坐标系中，标量亥姆霍兹方程为：
$∂2Ψ∂x2+∂2Ψ∂y2+∂2Ψ∂z2+k2Ψ=0\frac{\partial^2\Psi}{\partial x^2} + \frac{\partial^2\Psi}{\partial y^2} + \frac{\partial^2\Psi}{\partial z^2} + k^2\Psi = 0$

假设解的形式为：
$Ψ(x,y,z)=X(x)Y(y)Z(z)\Psi(x,y,z) = X(x)Y(y)Z(z)$

代入亥姆霍兹方程并分离变量，得到：
$1Xd2Xdx2+1Yd2Ydy2+1Zd2Zdz2+k2=0\frac{1}{X}\frac{d^2X}{dx^2} + \frac{1}{Y}\frac{d^2Y}{dy^2} + \frac{1}{Z}\frac{d^2Z}{dz^2} + k^2 = 0$

设：
$1Xd2Xdx2=−kx2,1Yd2Ydy2=−ky2,1Zd2Zdz2=−kz2\frac{1}{X}\frac{d^2X}{dx^2} = -k_x^2, \quad \frac{1}{Y}\frac{d^2Y}{dy^2} = -k_y^2, \quad \frac{1}{Z}\frac{d^2Z}{dz^2} = -k_z^2$

其中分离常数满足：
$k_x^2 + k_y^2 + k_z^2 = k^2$

A.2 横向本征函数

对于损耗壁边界条件，横向本征函数为：
$Xm(x)=Amcos⁡(kx,mx)+Bmsin⁡(kx,mx)X_m(x) = A_m\cos\left(k_{x,m}x\right) + B_m\sin\left(k_{x,m}x\right)$
$Yn(y)=Cncos⁡(ky,ny)+Dnsin⁡(ky,ny)Y_n(y) = C_n\cos\left(k_{y,n}y\right) + D_n\sin\left(k_{y,n}y\right)$

边界条件要求在壁面处电场切向分量连续，磁场切向分量连续。对于损耗壁，这导致复数本征值：
$kx,m=mπa(1+δx),ky,n=nπb(1+δy)k_{x,m} = \frac{m\pi}{a}\left(1 + \delta_x\right), \quad k_{y,n} = \frac{n\pi}{b}\left(1 + \delta_y\right)$

其中 $δx\delta_x$ 和 $δy\delta_y$ 是与壁材料参数相关的小修正项：
$δx≈1−j2ωμ02σ1a\delta_x \approx \frac{1-j}{\sqrt{2}}\sqrt{\frac{\omega\mu_0}{2\sigma}}\frac{1}{a}$

A.3 传播常数的确定

纵向传播常数由色散关系确定：
$kz,mn2=k02εrμr−kx,m2−ky,n2k_{z,mn}^2 = k_0^2\varepsilon_r\mu_r - k_{x,m}^2 - k_{y,n}^2$

对于 $EH_{mn}$ 模式：
$kz,mn=k02εr−(mπa)2−(nπb)2⋅(1+αmn+jβmn)k_{z,mn} = \sqrt{k_0^2\varepsilon_r - \left(\frac{m\pi}{a}\right)^2 - \left(\frac{n\pi}{b}\right)^2} \cdot (1 + \alpha_{mn} + j\beta_{mn})$

其中 $αmn\alpha_{mn}$ 表示额外衰减， $βmn\beta_{mn}$ 表示相位修正。

附录B：模式耦合系数的计算

B.1 重叠积分

两个模式之间的耦合系数定义为：
$Cmn,m′n′=∬Semn⋅em′n′∗dSC_{mn,m'n'} = \iint_S \mathbf{e}_{mn} \cdot \mathbf{e}^*_{m'n'} dS$

展开为分量形式：
$Cmn,m′n′=∫−a/2a/2∫−b/2b/2[Ex,mnEx,m′n′∗+Ey,mnEy,m′n′∗+Ez,mnEz,m′n′∗]dxdyC_{mn,m'n'} = \int_{-a/2}^{a/2}\int_{-b/2}^{b/2} \left[E_{x,mn}E^*_{x,m'n'} + E_{y,mn}E^*_{y,m'n'} + E_{z,mn}E^*_{z,m'n'}\right] dxdy$

B.2 准正交性的数学证明

对于小损耗情况（ $σ≪ωε0εr\sigma \ll \omega\varepsilon_0\varepsilon_r$ ），可以用微扰理论分析模式耦合。设无损情况下的本征函数为 $emn(0)\mathbf{e}^{(0)}_{mn}$ ，有损情况下的本征函数可展开为：
$emn=emn(0)+εemn(1)+ε2emn(2)+⋯\mathbf{e}_{mn} = \mathbf{e}^{(0)}_{mn} + \varepsilon\mathbf{e}^{(1)}_{mn} + \varepsilon^2\mathbf{e}^{(2)}_{mn} + \cdots$