当前位置：首页 > news >正文

用【C# + WinUI3 + 图像动画】来理解：高数 - 函数 - 初等函数

news 2025/9/21 6:06:37

函数分类

常数函数

绝对值函数

符号函数

阶梯曲线

多公式分段函数

函数类型总结

基本初等函数

幂函数

指数函数

对数函数

三角函数

反三角函数

学习感悟

作为一个高数小白，在学习函数这一节来说，最大的感受就是，怎么这么多公式，简直记不住，虽然中学的时候会学到这些知识，但是已经忘得一干二净了，并且完全不知道这些公式可以真的去用到什么地方，我可以用这些公式去达到哪些效果？

既然记不住公式，那么我希望通过图像化加深对它们的视觉记忆，转化为”感觉“、“直觉”。

函数分类

函数大致分为常数函数、绝对值函数、符号函数、阶梯曲线、分段函数，下面分别演示。

常数函数

例如公式 Y=2，不管自变量怎样变化（此处无自变量），因变量始终为一个固定的数值，映射到图像中可以是：从绝对变化图来看，不管坐标怎样变化，每个点颜色值始终相同；从增量变化图来看，不管坐标怎样变化，每一点的颜色值增量值始终相同。

那么 绝对变化图 和 增量变化图 两者的形态分别为：

这个函数简单到不需要特殊记忆，一看便知，视觉感觉：恒定、平稳、无奇。

WinUI3 部分处理代码：

private async Task ApplyDualImageEffect()
{if (originalPixelData == null) return; var incrementPixels = new byte[originalPixelData.Length];for (int i = 0; i < incrementPixels.Length; i += 4){incrementPixels[i] = ClampByte(originalPixelData[i] + incrementValue);     // BincrementPixels[i + 1] = ClampByte(originalPixelData[i + 1] + incrementValue); // GincrementPixels[i + 2] = ClampByte(originalPixelData[i + 2] + incrementValue); // RincrementPixels[i + 3] = originalPixelData[i + 3]; // A}var processedBitmap = await CreateBitmapFromPixelData(incrementPixels, imageWidth, imageHeight);ProcessedImage.Source = processedBitmap;
}

绝对值函数

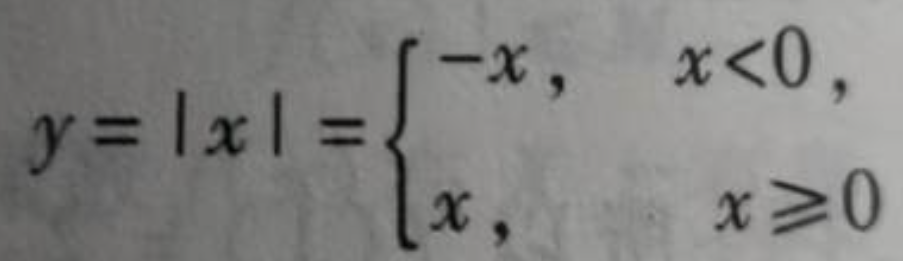
这个公式叫做绝对值函数，对它的理解方式是：

当自变量小于零的时候，因变量就取值为它的负数，

当自变量不小于0的时候，因变量就取值它本身。

那么映射到图像处理中，从绝对变化图效果来看，可以类似地理解为，颜色有效值范围是 0~255，假设以 128 为虚拟零点，当灰度值小于中间值128，那么取值为该点颜色值的对称值，以128为对称点，比如某个点的颜色值是 148 ，那么以 128 为对称点，将要取的值就是 108；当大于128的时候，则始终保持为它本身。同理，将该转换作为增量值附加到原图，比如 X 小于128的时候，增量值为固定的 -20，当 x 大于等于128 的时候增量值为固定的 20。

那么 绝对变化图 和 增量变化图 两者的形态分别为：

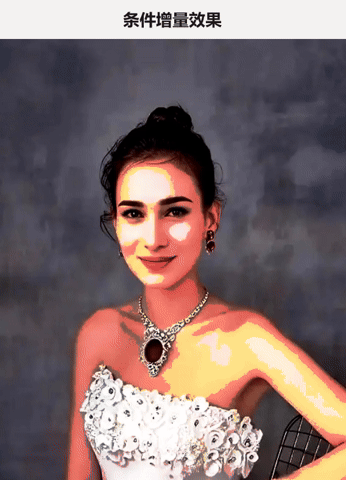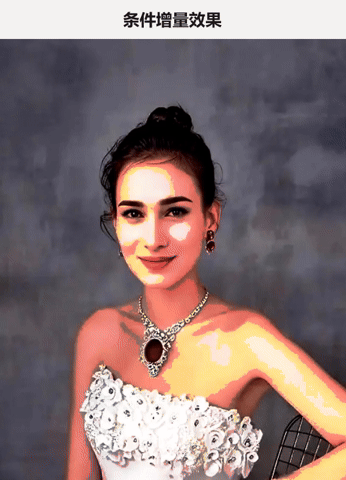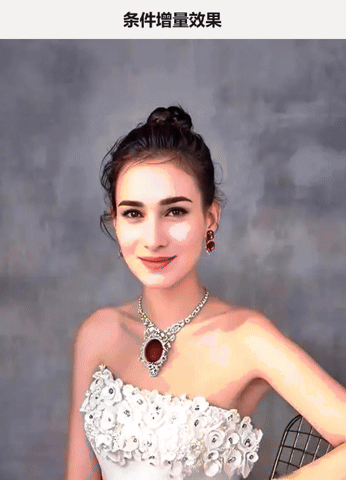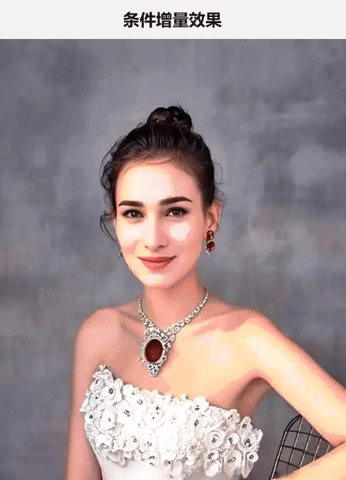左侧的绝对变化图：给人的感觉是：一部分做真正的自我，一部分做反向的自我，这样稍微有点变态的感觉，呈现出来的视觉效果也是有点诡异的；

左侧的增量变化图：给人的感觉是：一部分做真正的自我，一部分超越自我，这种自我+超我的感觉，清晰明亮，个性突出。

WinUI3 部分处理代码：

private byte ApplyAbsoluteFunction(byte value)
{// 以centerValue为中心，小于centerValue的值进行对称映射if (value < centerValue){// 计算对称值int symmetricValue = 2 * centerValue - value;// 确保值在有效范围内return (byte)Math.Min(255, Math.Max(0, symmetricValue));}else{// 大于等于centerValue的值保持不变return value;}
}

符号函数

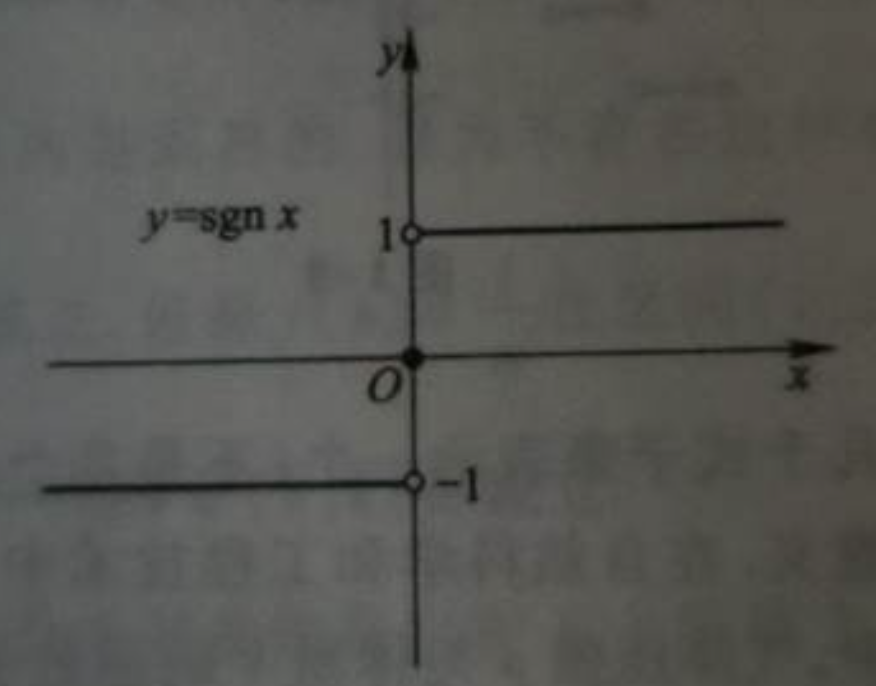
符号函数，和上面的绝对值函数有些类似，但是它的因变量的值与自变量本身无关联，它是一个固定的数值，比如说当 x 小于 0 的时候，x=0的时候，x>0的时候，因变量分别为三个不同的固定的数值。

那么映射到图像中，可以类似的理解为：仍然是把 128作为零点，从绝对变化图来说，当灰度值小于128 的时候，取值为 50，当灰度值等于128 的时候就取值为128，当灰度值大于128 的时候，就取值为 200 ；那么 绝对变化图 的形态为：

符号函数在少量的几个颜色值之间简单的变换目标色简单清晰

同样的，作用到增量变化图的效果上，当小于128 的时候，颜色值增量为固定的 -30 ，当等于128 的时候，颜色值不变，当大于128 的时候，增量为固定的 30 。那么 增量变化图 的形态为：

符号函数作为增量值加到图像上仍然破坏了颜色的自然过渡也呈现出了高的对比度

WinUI3 部分处理代码：

private byte ApplySignIncrement(byte value, int negativeInc, int zeroInc, int positiveInc)
{int newValue;if (value < CENTER_VALUE){newValue = value + negativeInc;  // 小于128时的增量}else if (value == CENTER_VALUE){newValue = value + zeroInc;       // 等于128时的增量}else{newValue = value + positiveInc;   // 大于128时的增量}// 确保值在有效范围内return (byte)Math.Min(255, Math.Max(0, newValue));
}

阶梯曲线

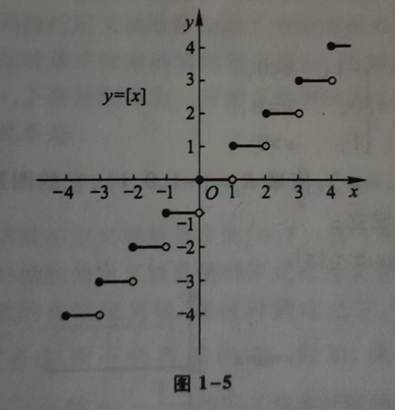
阶梯曲线，是当自变量在进行不同阶段的连续变化的时候，因变量取值为某一个集中的值。

比如，当自变量取值为1~2（包含小数）之间的时候，因变量就取值为1；自变量取值为 2~3 的时候，那么因变量取值为 2，也就是进行了取整操作。

可以看出来，因变量呈现出跳跃性的阶段性变化，像是楼梯一节一节的。那么映射到图像中，我们进行类似的如下处理：

由于颜色值是从0~255，它没有小数概念，因此我们把它抽象为：假设每隔 25 属于自变量的一个变化范围，那么因变量取值为该范围的下限，也就是说，颜色值从 0~25 之间的时候，因变量取值为0 ，颜色值取值为 25 到 50 的时候，就取值为 25 ，这样因变量的颜色值就会呈现阶段性的变化。

同理，用上面的处理方式作为增量值，但是由于按照上面范围下限作为增量值的话，颜色值会过太，极可能会无效，所以我们取为它的 1/10（或动态调节）来作为增量值，例如，当颜色值为0~25 的时候，增量为0；当颜色值为 25~50 的时候，增量值为 2.5；当颜色值为 200 到 225 的时候，增量值设置为 200的1/10，也就是10。

那么 绝对变化图 和 增量变化图 两者的形态分别为：

左侧的绝对变化图：给人的感觉是：好像手中只有颜色可怜的少数的几只画笔，把与画笔颜色接近的涂抹为同一个颜色，不同的颜色区域表现出了无法衔接的、不自然的过渡状态；

右侧的增量变化图：给人的感觉是：作为增量值时，视觉差异与普通增量效果差异并不是很明显，但是会看到接近的颜色变化范围也比较接近，不同的颜色区域表现出了比较明显的亮度层次差异。

WinUI3 部分处理代码：

 private byte ApplyStepIncrement(byte value){// 计算当前值所在的阶梯int stepNumber = value / currentStepSize;int stepBase = stepNumber * currentStepSize;// 增量为阶梯下限值的1/n（n为可调参数）double increment = stepBase / (double)currentIncrementRatio;// 应用增量int newValue = value + (int)Math.Round(increment);// 确保值在有效范围内return (byte)Math.Min(255, Math.Max(0, newValue));}

多公式分段函数

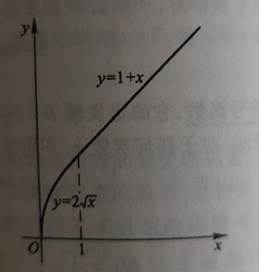
前面讲到的符号函数和阶梯函数，它们都属于是分段函数，在不同的自变量的阶段范围内，因变量发生了对应的变化，但是上面两种情况直接使用了具体的数值，这里我们也可以把它换成公式，也就是说，当自变量在第 1 个范围时，应用公式a，当自变量在第 2 个范围时，应用公式b ，即在不同的情形使用不同的公式转换。

把它映射到图像中，我们可以类似这样处理：对于绝对变化图来说，如果当前的颜色值小于128，则对这个颜色值进行开平方计算, 然后再乘以 2 ，即 y=2√x；如果当前的颜色值大于等于128 时，则对这个颜色值进行加30 的计算 , 也就是 y=30+x，那么 绝对变化图 的处理结果为：

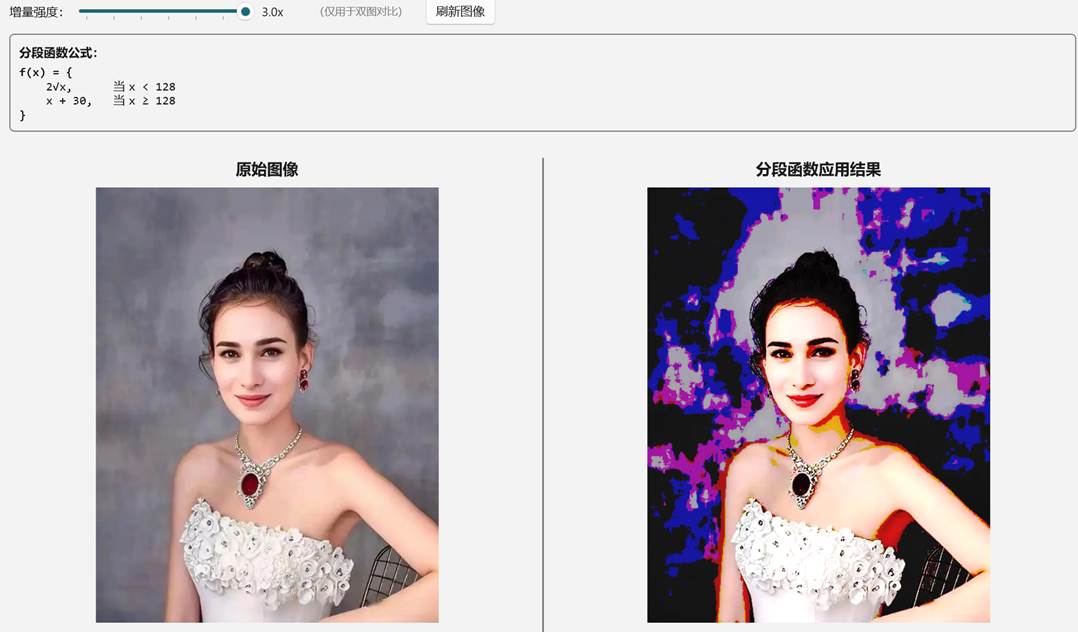
同理，用上面的处理方式作为增量值，处理后的形态为：

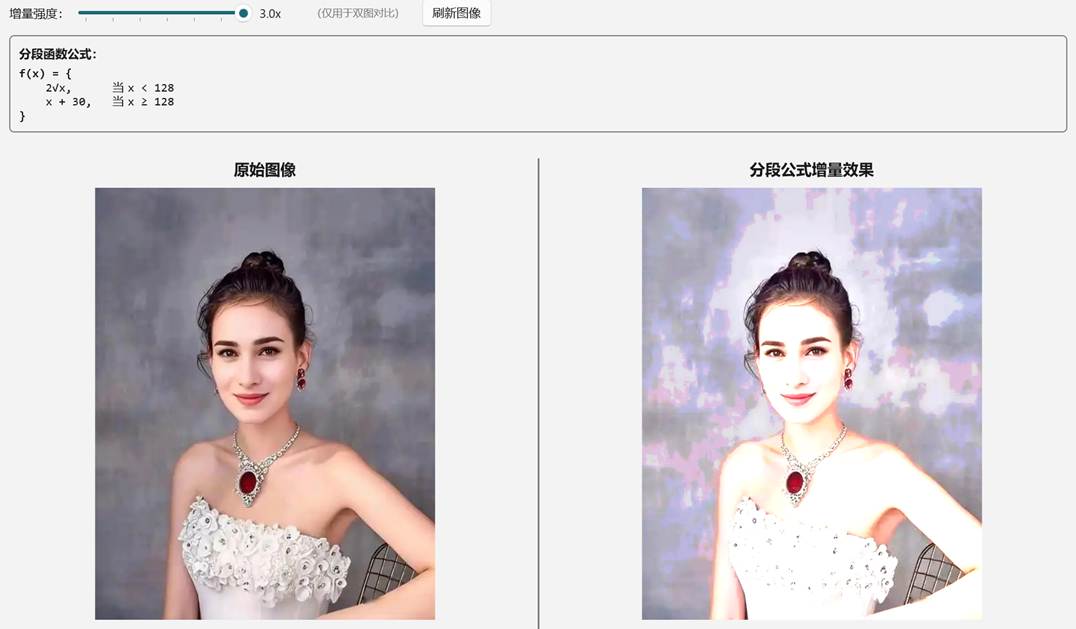
WinUI3 部分处理代码：

 private byte ApplyPiecewiseFunction(byte value){double result;if (value < THRESHOLD){ result = 2 * Math.Sqrt(value);}else{ result = value + 30;}  return (byte)Math.Min(255, Math.Max(0, Math.Round(result)));}

函数类型总结

以上提到的是函数的基本类型，它们具有 4 个方面的特性：有界性、单调性、奇偶性、周期性，并且对以上的函数进行反向（逆向）的处理，即为反函数 ，把它们进行一些组合使用，又称为复合函数 ，对多种不同的函数进行和差积商，又可以进行 函数运算。

基本初等函数

了解了函数的基本分类之后，每种类型里的具体函数是多种多样的，有简单的、复杂的，一些常见的函数包含：幂函数、指数函数、对数函数、三角函数、反三角函数，这五类称为 基本初等函数。接下来我们来了解具体的公式。

幂函数

幂函数, 对自变量进行指定次数的乘法计算。表现在图像上就是，对每个颜色值进行n次方计算，假设n动态可调整，那么处理效果为：

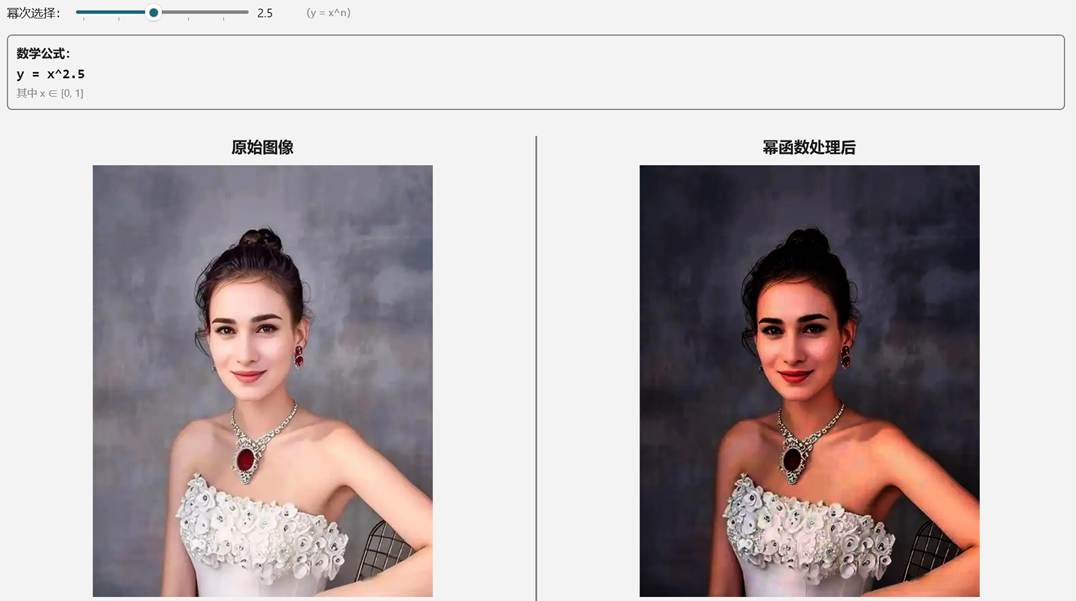
WinUI3 部分处理代码：

private byte ApplyPower(byte value)
{// 将像素值归一化到 [0, 1] 范围double normalized = value / 255.0; // 应用幂函数 y = x^ndouble result = Math.Pow(normalized, currentPower); // 将结果映射回 [0, 255] 范围return (byte)Math.Round(result * 255);
}

指数函数

指数函数，由于需要把自变量作为指数，因此把它映射到图像中后，颜色的值需要作为自变量指数，假设对2进行指数的运算 , 指数来自于每个点的颜色值，这样得到的结果数值可能太大，远远超出了255，因此为了能够显示它们，我们取值为除以256之后的余数。处理效果为：

WinUI3 部分处理代码：

private byte ApplyExponential(byte value)
{// 使用缩放因子来控制指数增长的速度// 缩放因子越小，增长越缓慢，效果越温和double scaledValue = value * scaleFactor; // 计算指数函数double result = Math.Pow(currentBase, scaledValue); // 由于即使使用缩放因子，结果仍可能很大，使用模256运算// 这样可以产生周期性的振荡效果int moduloResult = (int)(result % 256); return (byte)moduloResult;
}

对数函数

基于指定的底数，把每个点的颜色值作为自变量来进行对数函数处理效果：

WinUI3 部分处理代码：

private byte ApplyLogarithm(byte value)
{// 对数函数：log(0)未定义，所以加1避免// 对于不同的底数，对数曲线的陡峭程度不同double inputValue = value + 1;  // 避免 log(0) // 计算对数值double logValue = Math.Log(inputValue) / Math.Log(currentBase); // 使用增强系数来放大效果double scaledValue = logValue * enhanceFactor; // 确保结果在有效范围内return (byte)Math.Min(255, Math.Max(0, Math.Round(scaledValue)));
}

三角函数

y=sin x , y =cos x, y=tan x, y=cotan x

假设我们用这4个三角函数按照如下公式进行计算，并且可动态调整参数：

sin: y = 128 + amplitude × sin(frequency × x)

cos: y = 128 + amplitude × cos(frequency × x)

tan: y = 128 + amplitude × tan(frequency × x)

cot: y = 128 + amplitude × cot(frequency × x)

那么可处理为不同的效果：

动态调整参数，可以看到炫丽且怪异的图像效果，它们呈现周期性变化、具有波纹和震荡的视觉效果，太另类了，有点欣赏不来，看来我不喜欢三角函数的美：

WinUI3 部分处理代码：

 private byte ApplyTan(byte value)
{// 计算 tan 函数，需要处理垂直渐近线double radians = value * tanFrequency;double tanValue = Math.Tan(radians); // 限制 tan 值的范围，避免过大的值tanValue = Math.Max(-3.0, Math.Min(3.0, tanValue)); // 应用振幅并中心化到128double result = 128.0 + tanAmplitude * tanValue; return (byte)Math.Min(255, Math.Max(0, Math.Round(result)));
}

反三角函数

Y=arcsin x , y =arccos x, y=arctan x, y=arccotan x

假设我们用这4个反三角函数按照如下公式进行计算，并且可动态调整参数（将像素映射到角度范围，产生周期性效果）：

arcsin: y = offset + scale × arcsin((x-128)/128)

arccos: y = offset + scale × arccos((x-128)/128)

arctan: y = offset + scale × arctan((x-128)/16)

arccot: y = offset + scale × arccot((x-128)/16)

那么可处理为不同的效果：

动态调整参数，可以看到优美的图像效果，反三角函数看起来比三角函数 “正派” 多了：

WinUI3 部分处理代码：

private byte ApplyArcsin(byte value)
{// 将像素值映射到 [-1, 1] 范围double normalized = (value - 128.0) / 128.0;normalized = Math.Max(-1.0, Math.Min(1.0, normalized)); // 限制在定义域内 // 计算 arcsin，结果在 [-π/2, π/2] 范围double result = Math.Asin(normalized); // 应用缩放和偏移double scaledResult = arcsinOffset + arcsinScale * result; return (byte)Math.Min(255, Math.Max(0, Math.Round(scaledResult)));
}