速通ACM省铜第十天 赋源码(A Good Problem和Make It Beautiful和Gellyfish and Baby‘s Breath)
目录
引言:
A Good Problem
题意分析
逻辑梳理
代码实现
Make It Beautiful
题意分析
逻辑梳理
代码实现
Gellyfish and Baby's Breath
题意分析
逻辑梳理
代码实现
结语:
引言:
今天周六了,那没课就多打几题吧,但为了不跟之前刷题强度差距过大,我最终决定开三道1300的题目,每道题都不是很难,具体三题如图

那么接下来,我们就按照上面的顺序进入今天的算法题讲解吧(我感觉第三题是这三题里最难的,另外俩题都还好)——————>

A Good Problem
按照惯例,我们先看题目
题意分析
题目链接在这Problem - 2119C - Codeforces
不想跳转的可以看下图

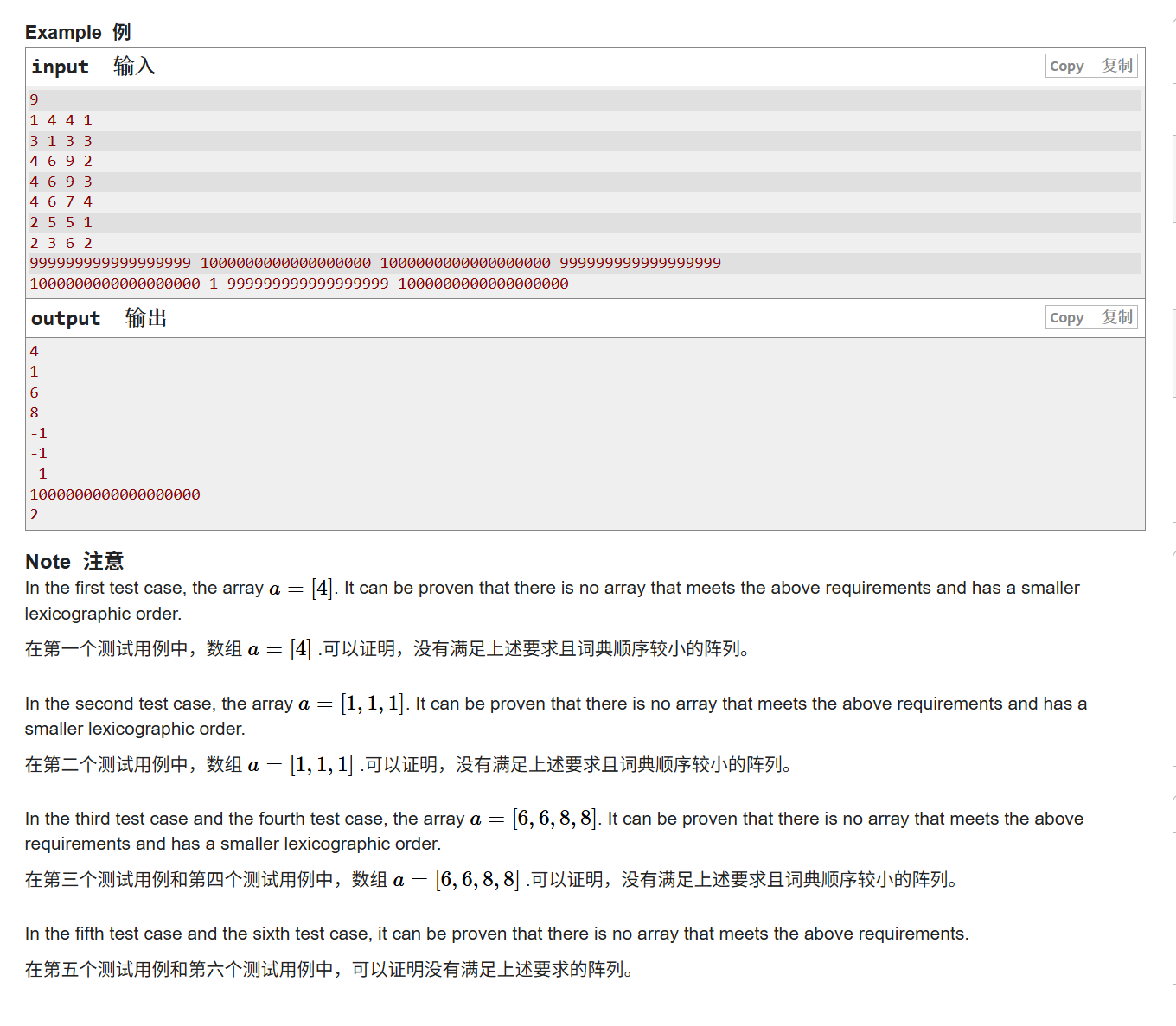
题目的意思很简单,就是给你一个取值范围(即l到r),然后让你创建一个长度为n的数组,这个数组需要满足将每个数组中的元素从前往后与的结果要跟从前往后异或得到的结果一样,问你能不能创建出这个数组,如果可以创建出来,就输出数组中第k个元素的值,若不可以创建出来,就输出-1即可,那么接下来我们就进入逻辑梳理环节
逻辑梳理
首先,我们可以将数组长度分为偶数和奇数两种情况,对同一个数进行异或偶数次,最终结果依旧是这个数,若对一个数进行异或奇数次,这得到的最终值为0
所以我们将数组长度分为奇数与偶数俩种情况
奇数时:当对异或了偶数次的时候,因为算上他自身本身,所以有奇数的长度,此时不管需要输出哪个数组的位置,因为都是同一个数,所以直接输出范围内的一个值即可,我在这种情况时输出下限l
偶数时:这种情况也好解决,我们已经知道了奇数个数异或的时候得到的是原数,偶数个数异或时候得到的是0,因为偶数时候不好控最后的值,所以我们尽量让异或和与最后的结果都为0
那么我们先来看&如何能变成0:其实很简单,就是偶数个是同一个数,剩余的偶数个就选与第一个数&后结果是0的一个数,即可以变成0了,如图
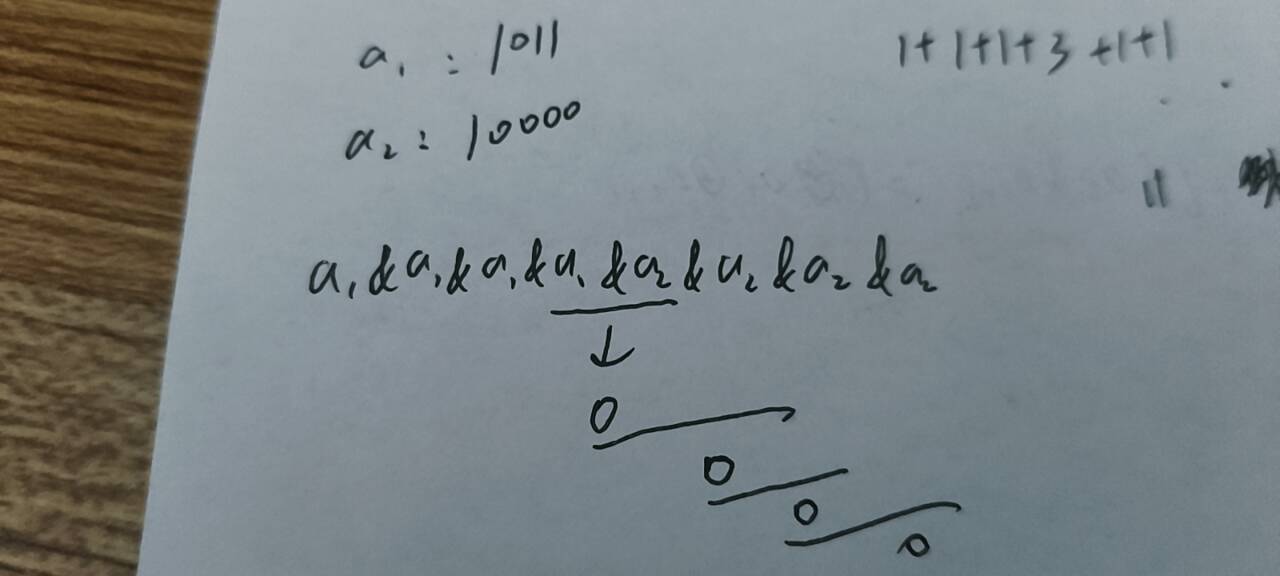
接下来我们再看异或如何能变成0:这个其实顺着&的思路其实就直接出来了,依旧是前面偶数个,剩余偶数个,最后结果自然就是0了,因为前面偶数个相同数异或得到0,再异或偶数个相同数又会变成0。
那么,偶数个时的操作我们就确定了,需要2个不同的数各偶数个,那么自然,如果数组内元素只有2个的话,自然就没法达到目的,输出-1
那么,具体我们怎么生成这俩个数呢,我们可以前面的全是同一个数,剩余的最后俩个元素用另一个数,前面的数我们可以取范围内的下限l,这样后面的数才可以尽可能小。
那么第二个数怎么选呢,因为要让俩个数&后的结果为0,所以第二个数最小应该是比第一个数高一位的2的位次,如上图的a1若为第一个数,那么a2变为第二个数。
此时,我们只需要判断第二个数有没有超出上限即可,若没有超出上限,就输出要求的位置的元素,若超出了,就输出-1即可
那么,该题的逻辑就理清楚啦,接下来就进入代码实现的部分
代码实现
这题的代码还是很简单的,那么我们就直接看AC码吧
就是需要注意的是转二进制时候不需要全部转出来,甚至都不需要转,只需要找到最高位的下一位即可,即下方代码中的jinzhuan函数的功能
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <iostream>
#include <string.h>
#include <algorithm>
#include <math.h>
#include <queue>
#include <vector>
using namespace std;int t;long long jinzhuan(long long l)
{long long T = 1;for (int i = 0; i < 100; i++){if (T > l){return T;}T *= 2;}}void solve()
{long long n, l, r, k;cin >> n >> l >> r >> k;if (n % 2){cout << l << endl;return;}long long fan = jinzhuan(l);if (n == 2 || fan > r){cout << "-1" << endl;return;}if (k <= n - 2)cout << l << endl;else{cout << fan << endl;}
}int main()
{cin >> t;while (t--){solve();}return 0;
}那么,这题就讲完啦,接下来我们来看下一题
Make It Beautiful
题意分析
题目链接在这里Problem - 2118C - Codeforces
不想跳转的可以看下图

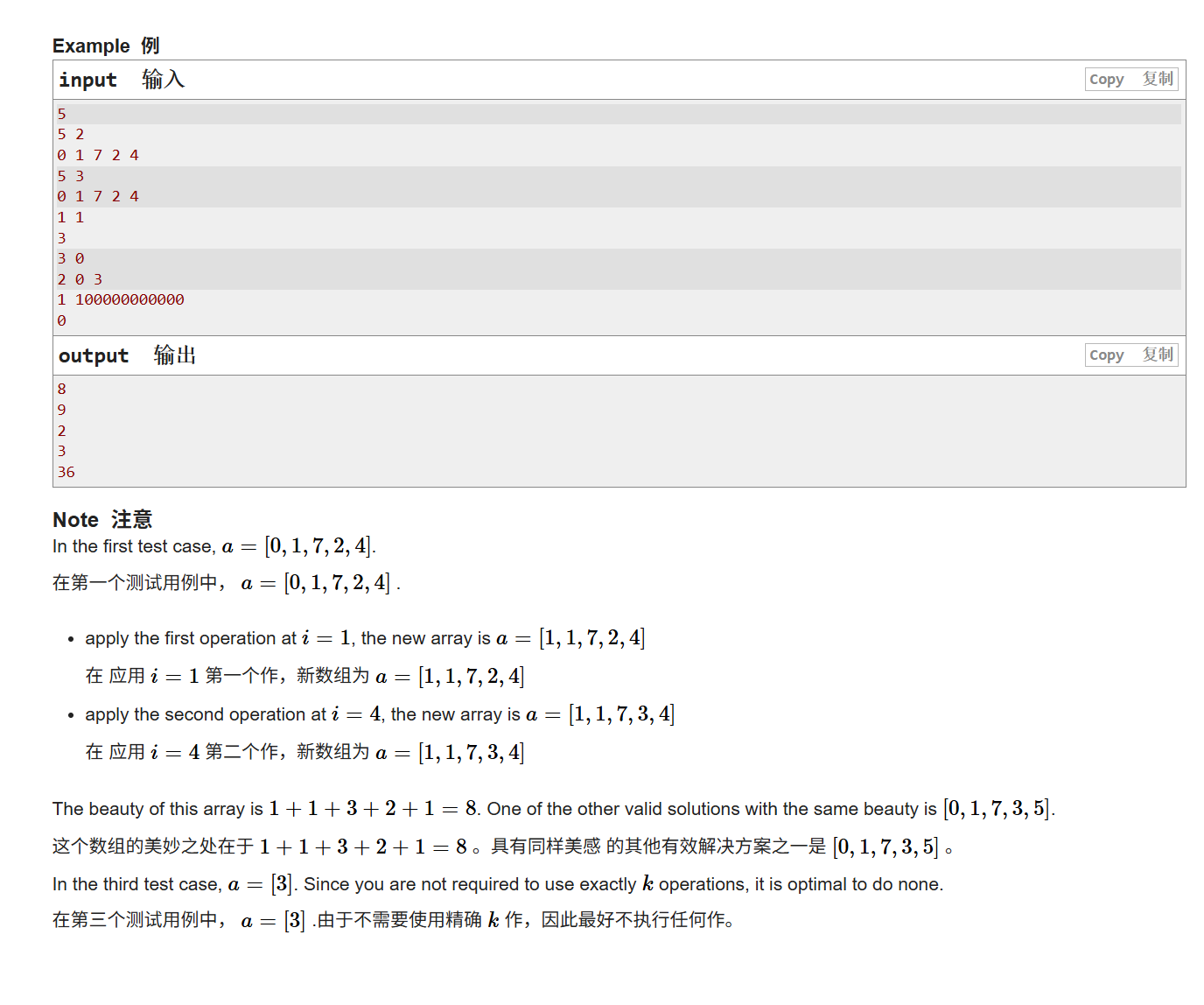
这题题目依旧很短,就是先给你一个长度为n的数组和可以操作的次数k,然后再输入数组中的元素。
可以对数组进行操作,每次操作都可以对数组里的一个元素进行+1操作,最后输出在不超过k次操作的情况下,整个数组的最大值
数组的值为每个元素转为2进制后1的个数相加得到的最终值。
题目的意思就这么简单,接下来我们进行逻辑的梳理
逻辑梳理
这题,我们首先需要将所有的元素转换成二进制数。
在二进制中,如果想要将0变成1,且不影响其他位1的个数的时候,需要加2的位次,如图,就需要加2的3次,即需要操作8次
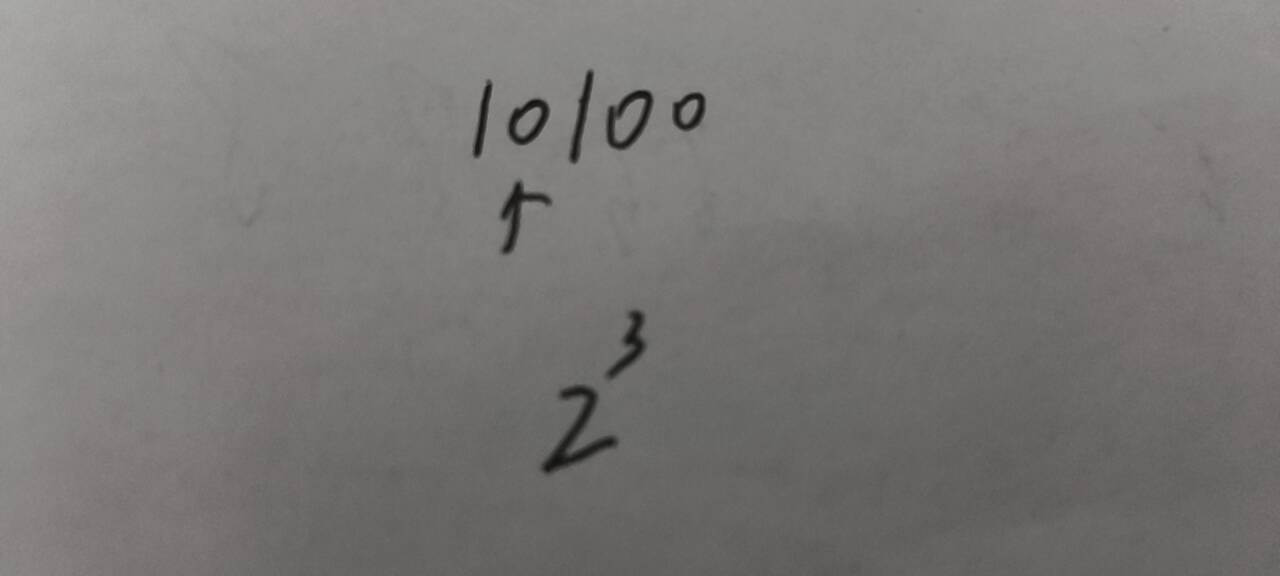
知道了这一点后,我们将一个元素拓展到数组的n个元素
我们可以将每个元素转换成二进制后,将每个位是1的个数存储起来,然后从小往大遍历
因为一个位上1的个数最多为n个,若不足n个就可以进行操作。
从小往大遍历是因为位数小需要的操作次数就少,性价比就高
接下来我们只需要将操作次数全部用在1的生成上就可以啦
那么,这道题的逻辑就梳理完啦,接下来进入代码实现环节
代码实现
经过上面逻辑的讲解,应该都会打了,只需要注意一点,那就是数组一定要开的大,不要开小,开小会WA,我就因为这个WA了一次(哭死
那么接下来,就直接放AC码啦
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <iostream>
#include <string.h>
#include <algorithm>
#include <math.h>
#include <queue>
#include <vector>
using namespace std;int t;
int a[71];
long long ans;void jinzhuan(long long l)
{for (int i = 30; i >= 0; i--){if (pow(2, i) <= l){l -= pow(2, i);a[i]++;ans++;}}}void solve()
{ans = 0;memset(a, 0, sizeof(a));long long n, k, l;cin >> n >> k;for (int i = 1; i <= n; i++){cin >> l;jinzhuan(l);}for (int i = 0; i <= 70; i++){if (a[i] <= n){if (k - (n - a[i])*pow(2,i) > 0){k -= (n - a[i]) * pow(2, i);ans += n - a[i];continue;}ans += k / pow(2, i);break;}}cout << ans << endl;
}int main()
{cin >> t;while (t--){solve();}return 0;
}这题也讲解完啦,接下来就是最后一题
Gellyfish and Baby's Breath
这题的代码实现我会分俩步进行讲解,第一步是TLE码,第二步是AC码,接下来我们先看题目
题意分析
题目链接在这里Problem - 2116B - Codeforces
不想跳转的可看下图

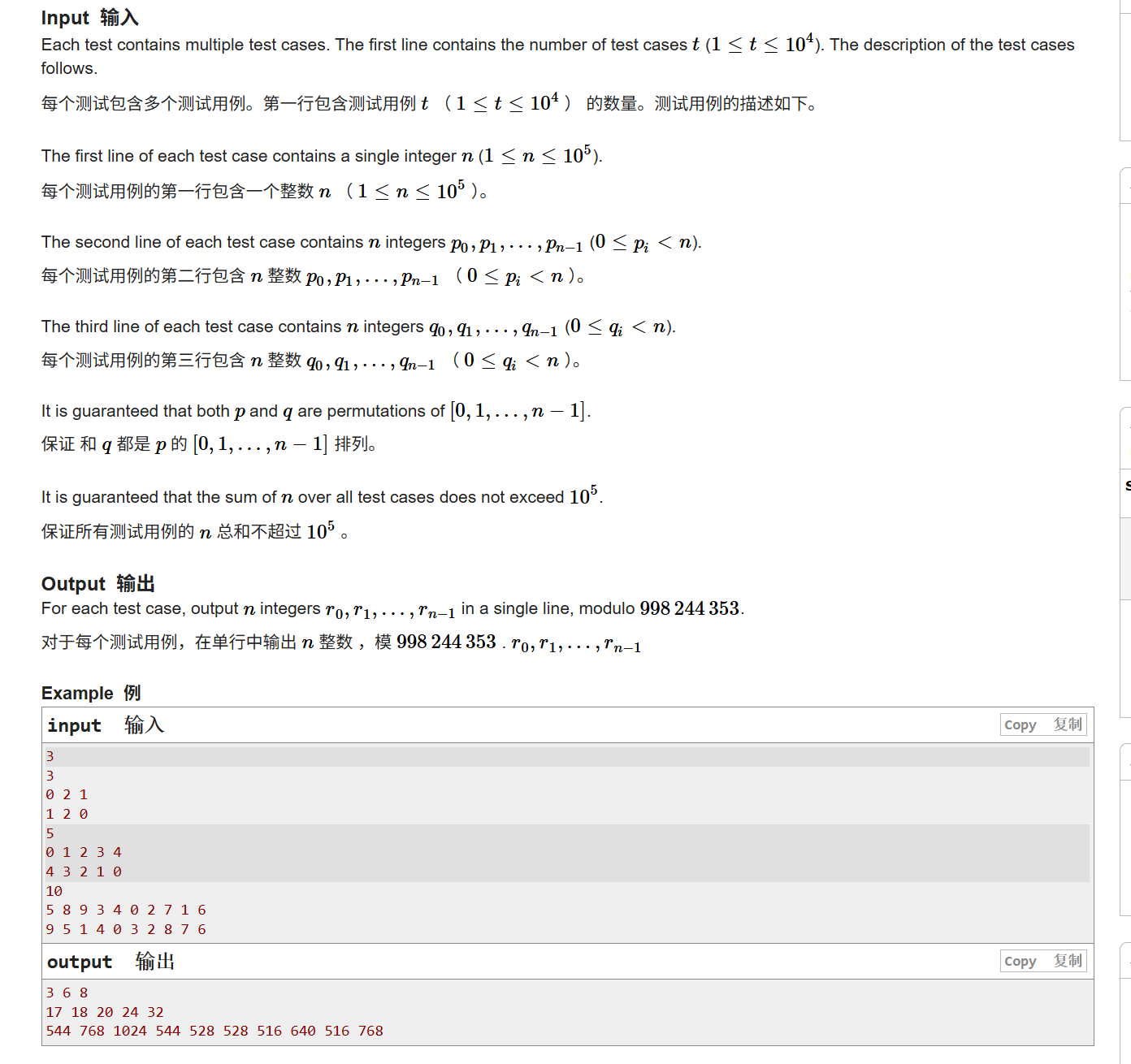
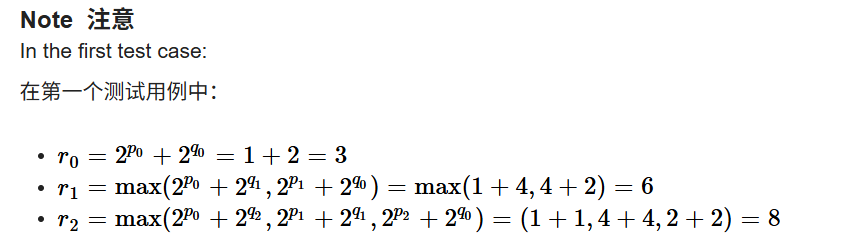
题目想要表达的意思其实很简单,先告诉你数组长度为多少,然后给你俩个数组
这俩个数组的元素的范围都为0-n-1,也可以把这俩个数组理解为是将0-n-1的元素进行打乱后的俩个数组
题目要求我们得到一个新的数组c,然后输出c数组的每个元素
如何得到新数组c,简单点说就是将俩个数组的每个下标一一对齐,然后用对角线的感觉找出最大值,值的运算就是2的pi次加上2的qj-i+1次,讲的可能有点抽象,我们借助图来理解,如图,c数组中第四个元素的值就是这四条线中最大的值,值得运算便是2的p[i]次加上2的q[4-i]次
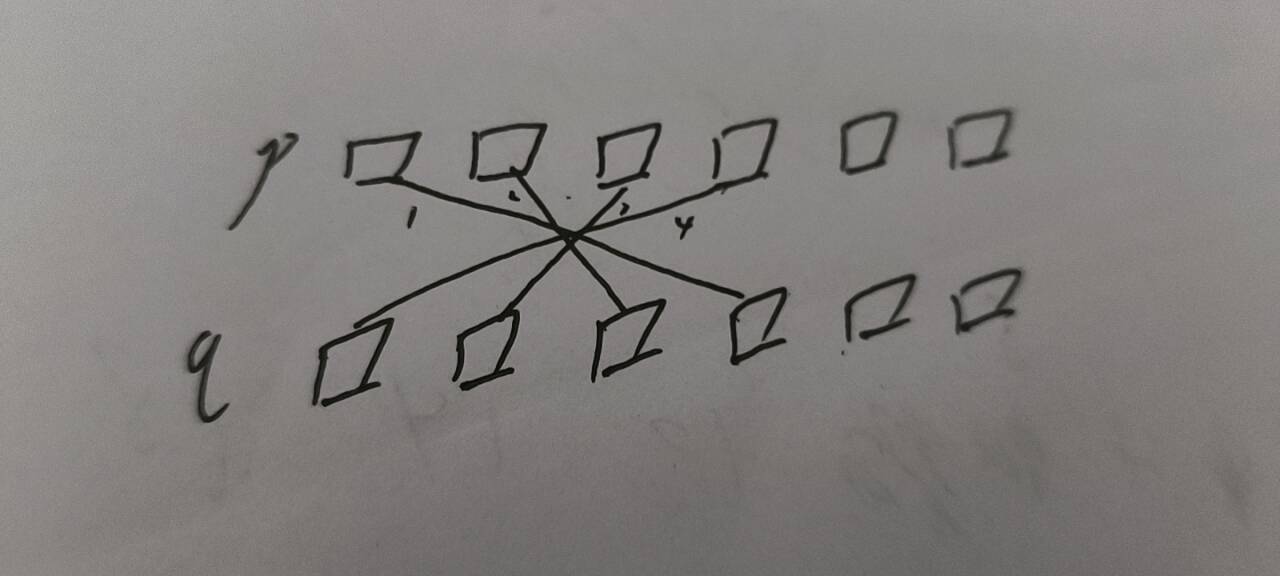
那么,题目的意思我们已经分析完了,接下来进入逻辑梳理环节
逻辑梳理
首先我们既然看到跟2的幂次有关的式子,首先就是想到跟2进制有关,但是题目数据这么大,转或者乘都是不可取的,那么我们就只能通过宏观的判断来观察规律
很明显,我们只需要找到在i位长度下,p,q俩个数组在其中的最大的值即可,因为位越高,值越大,找到位最高的,然后再通过对角法找到对应的另一个数组的位即可
若在这个范围内,俩个数组最大的纸都一样,那么就看这俩种情况下,对应的另外一组数组中的值的大小进行比较,哪个大就选择哪个即可。
那么怎么看前i个元素中的最大值呢,我们可以用遍历迭代来解决,如果新进来的元素比之前该数组当前最大元素的下标所对应的值来的大,就将最大元素下标进行更新即可,然后之后具体操作时候只需要使用最大元素下标来进行操作就可以了
最后我们只需要在每次循环结束时输出对应得到的值即可。
当然需要注意的是,因为值很大,每次运算完都要进行取模操作
那么该题的思路已经理完了,接下来我们进入代码实现环节
代码实现
在得到AC码前,我们先讲一下TLE码,因为AC码是在TLE码的优化后才得到的
TLE代码
首先便是我们用上面的思路打出来的最原始的代码,也就是这个代码
该代码中a,b为初始俩数组,c为最终需要输出的数组
然后maxa和maxb这俩个变量便是分别代表目前a,b俩数组最大值的下标,会进行持续的更新迭代
然后就是各种情况的判断和运算,最终就得出了如下代码
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <iostream>
#include <string.h>
#include <algorithm>
#include <math.h>
#include <queue>
#include <vector>
using namespace std;int t;
int a[100010];
int b[100010];
int c[100010];void solve()
{int n;cin >> n;for (int i = 1; i <= n; i++)cin >> a[i];for (int i = 1; i <= n; i++)cin >> b[i];int maxa = 1;int maxb = 1;for (int i = 1; i <= n; i++){if (a[i] > a[maxa])maxa = i;if (b[i] > b[maxb])maxb = i;if (a[maxa] > b[maxb]){c[i] = 1;for (int j = 1; j <= a[maxa]; j++){c[i] = c[i] * 2 % 998244353;}long long ll = 1;for (int j = 1; j <= b[i - maxa + 1]; j++){ll = ll * 2 % 998244353;}c[i] = (c[i] + ll) % 998244353;}else if (a[maxa] < b[maxb]){c[i] = 1;for (int j = 1; j <= b[maxb]; j++){c[i] = c[i] * 2 % 998244353;}long long ll = 1;for (int j = 1; j <= a[i - maxb + 1]; j++){ll = ll * 2 % 998244353;}c[i] = (c[i] + ll) % 998244353;}else{if (a[i - maxb + 1] > b[i - maxa + 1]){c[i] = 1;for (int j = 1; j <= b[maxb]; j++){c[i] = c[i] * 2 % 998244353;}long long ll = 1;for (int j = 1; j <= a[i - maxb + 1]; j++){ll = ll * 2 % 998244353;}c[i] = (c[i] + ll) % 998244353;}else{c[i] = 1;for (int j = 1; j <= a[maxa]; j++){c[i] = c[i] * 2 % 998244353;}long long ll = 1;for (int j = 1; j <= b[i - maxa + 1]; j++){ll = ll * 2 % 998244353;}c[i] = (c[i] + ll) % 998244353;}}cout << c[i] << " ";}cout << endl;
}int main()
{cin >> t;while (t--){solve();}return 0;
}这个代码不仅看着又臭又长,而且还会TLE在第三个样例,如图

为什么会这样呢,因为我们每次在运算时候都进行了a[maxa]和b[maxb]次的循环,这个循环是基于n长度下的,所以时间复杂度已经很明显会超标了,那么,我们就得想办法预处理,使得a[maxa]和b[maxb]这俩个不管怎么变,都可以直接出结果而不是经过运算再出结果
那么具体怎么操作呢,我们可以定义一个新的函数,来预处理2的不同位次时取模后的结果,之后只需要直接调用这个就可以了,然后再在相加完后取模即可,这样时间复杂度就会低一大层,相当于3层变俩层,每次操作都只是O(n)的时间复杂度,自然就不会超时了
那么接下来,我们就来看该题的AC码
AC码
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <iostream>
#include <string.h>
#include <algorithm>
#include <math.h>
#include <queue>
#include <vector>
using namespace std;int t;
long long a[100010];
long long b[100010];
long long c[100010];
long long d[100010];void solve()
{int n;cin >> n;for (int i = 1; i <= n; i++)cin >> a[i];for (int i = 1; i <= n; i++)cin >> b[i];int maxa = 1;int maxb = 1;for (int i = 1; i <= n; i++){if (a[i] > a[maxa])maxa = i;if (b[i] > b[maxb])maxb = i;if (a[maxa] > b[maxb]){c[i] = (d[a[maxa]] + d[b[i - maxa + 1]]) % 998244353;}else if (a[maxa] < b[maxb]){c[i] = (d[a[i - maxb + 1]] + d[b[maxb]]) % 998244353;}else{if (a[i - maxb + 1] > b[i - maxa + 1]){c[i] = (d[a[i - maxb + 1]] + d[b[maxb]]) % 998244353;}else{c[i] = (d[a[maxa]] + d[b[i - maxa + 1]]) % 998244353;}}cout << c[i] << " ";}cout << endl;
}int main()
{cin >> t;d[0] = 1;for (int i = 1; i <= 100000; i++){d[i] = d[i - 1] * 2 % 998244353;}while (t--){solve();}return 0;
}优化过的码是不是相比于TLE的码看起来也简洁了许多,不再那么又臭又长了
那么,这题的讲解也结束啦
结语:
今日算法讲解到此结束啦,希望对你们有所帮助,谢谢观看,如果觉得不错可以分享给朋友哟。当然也可以关注一下,有什么看不懂的可以评论问哦

