Java优选算法——前缀和

一、⭐️【模板】前缀和

题目链接：https://www.nowcoder.com/practice/acead2f4c28c401889915da98ecdc6bf?tpId=230&tqId=2021480&ru=/exam/oj&qru=/ta/dynamic-programming/question-ranking&sourceUrl=%2Fexam%2Foj%3Fpage%3D1%26tab%3D%25E7%25AE%2597%25E6%25B3%2595%25E7%25AF%2587%26topicId%3D196

题目：

描述
对于给定的长度为 n 的数组 {a1​,a2​,…,an​}，我们有 m 次查询操作，每一次操作给出两个参数 l,r，你需要输出数组中第 l 到第 r 个元素之和，即 al​+al+1​+⋯+ar​。

 

输入描述：
第一行输入两个整数 n,m（1≤n,m≤105）代表数组中的元素数量、查询次数。
第二行输入 n 个整数 a1​,a2​,…,an​（−109≤ai​≤109）代表初始数组。
此后 m 行，每行输入两个整数 l,r（1≤l≤r≤n）代表一次查询。

 

输出描述：
对于每一次查询操作，在一行上输出一个整数，代表区间和。

 

示例 1
输入：3 2
1 2 4
1 2
2 3
输出：3
6

---

思路：

先看暴力解法：

每次求下标l到r的元素之和，只需要一次遍历数组即可，总的时间复杂度为O(n)*O(q)。

前缀和算法：

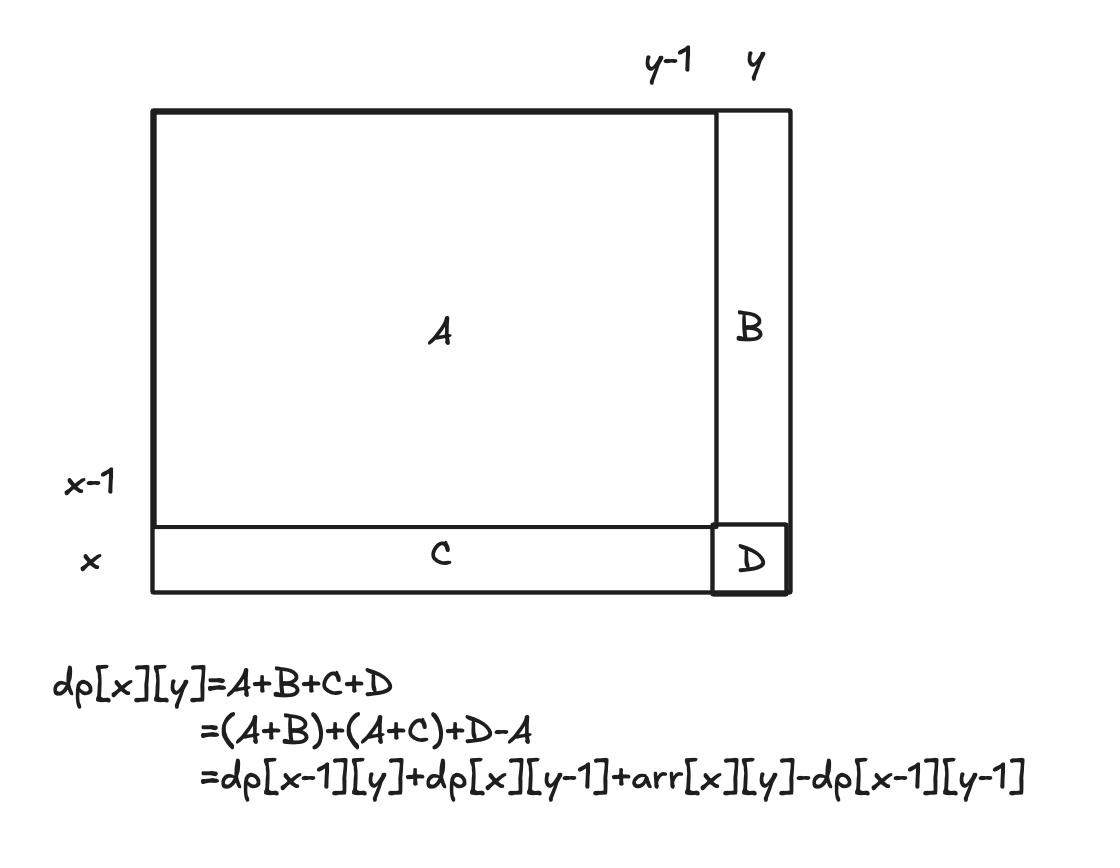
⭐️先构建出一个前缀和数组dp[]，其中dp[i]表示的是[1,i]区间内的所有元素之和（因为会出现dp[i-1]当i=0时，索引出现错误的情况，增加数组的大小来避免了分类讨论,而dp[0]可以额外声明 为多少）。

有dp[i]=dp[i-1]+arr[i]，其中dp[0]=0;

因为题目给出的l≥1，这里dp的下标从1开始填入。

则dp[r]-dp[l-1]为最终结果，该算法的时间复杂度为O(n)+O(q)。

---

代码及结果：

import java.util.Scanner;// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {public static void main(String[] args) {Scanner in = new Scanner(System.in);int n=in.nextInt();int q=in.nextInt();int []arr=new int[n+1];//数组有效元素的下标从1开始for(int i=1;i<n+1;i++){arr[i]=in.nextInt();}//预处理一个前缀和数组long []dp=new long[n+1];for(int i=1;i<n+1;i++){dp[i]=dp[i-1]+arr[i];}while(q>0){int l=in.nextInt();int r=in.nextInt();System.out.println(dp[r]-dp[l-1]);q--;}}
}

---

二、⭐️【模板】二维前缀和

题目链接：https://www.nowcoder.com/practice/99eb8040d116414ea3296467ce81cbbc?tpId=230&tqId=2023819&ru=/exam/oj&qru=/ta/dynamic-programming/question-ranking&sourceUrl=%2Fexam%2Foj%3Fpage%3D1%26tab%3D%25E7%25AE%2597%25E6%25B3%2595%25E7%25AF%2587%26topicId%3D196

题目：

描述
给定一个由 n 行 m 列整数组成的矩阵 {ai,j​}（下标均从 1 开始）。
现有 q 次独立查询，第 k 次查询给定四个整数 x1​,y1​,x2​,y2​，表示左上角坐标 (x1​,y1​) 与右下角坐标 (x2​,y2​) 满足 1≤x1​≤x2​≤n 且 1≤y1​≤y2​≤m。
请你计算该子矩阵中全部元素之和，记为
S(x1​,y1​,x2​,y2​)=∑i=x1​x2​​∑j=y1​y2​​ai,j​。
你需要依次回答所有查询。

 

输入描述：
在一行上输入三个整数 n,m,q（1≤n,m≤103；1≤q≤105），依次表示矩阵的行数、列数与查询次数。
此后 n 行，每行输入 m 个整数 ai,1​,ai,2​,…,ai,m​（−109≤ai,j​≤109），表示矩阵第 i 行的元素；共计 n×m 个整数。
此后 q 行，每行输入四个整数 x1​,y1​,x2​,y2​，所有变量均满足
1≤x1​≤x2​≤n，1≤y1​≤y2​≤m。

 

输出描述：
对于每一次查询，在一行上输出一个整数，表示对应子矩阵元素之和。

 

示例 1
输入：3 4 3
1 2 3 4
3 2 1 0
1 5 7 8
1 1 2 2
1 1 3 3
1 2 3 4
输出：8
25
32
说明： 以第一组样例中的第二次查询 (x1​,y1​,x2​,y2​)=(1,1,3,3) 为例：
●查询的子矩阵包含矩阵的左上 3×3 区域；
●其内部所有元素之和为 1+2+3+3+2+1+1+5+7=25；
因此输出 25。

 

备注：
读入数据可能很大，请注意读写时间。

---

思路：

假如有以下二维数组，下面是构建二维前缀和数组dp[]：

dp[x][y]表示从(1,1)到(x,y)之间矩阵中的元素之和。

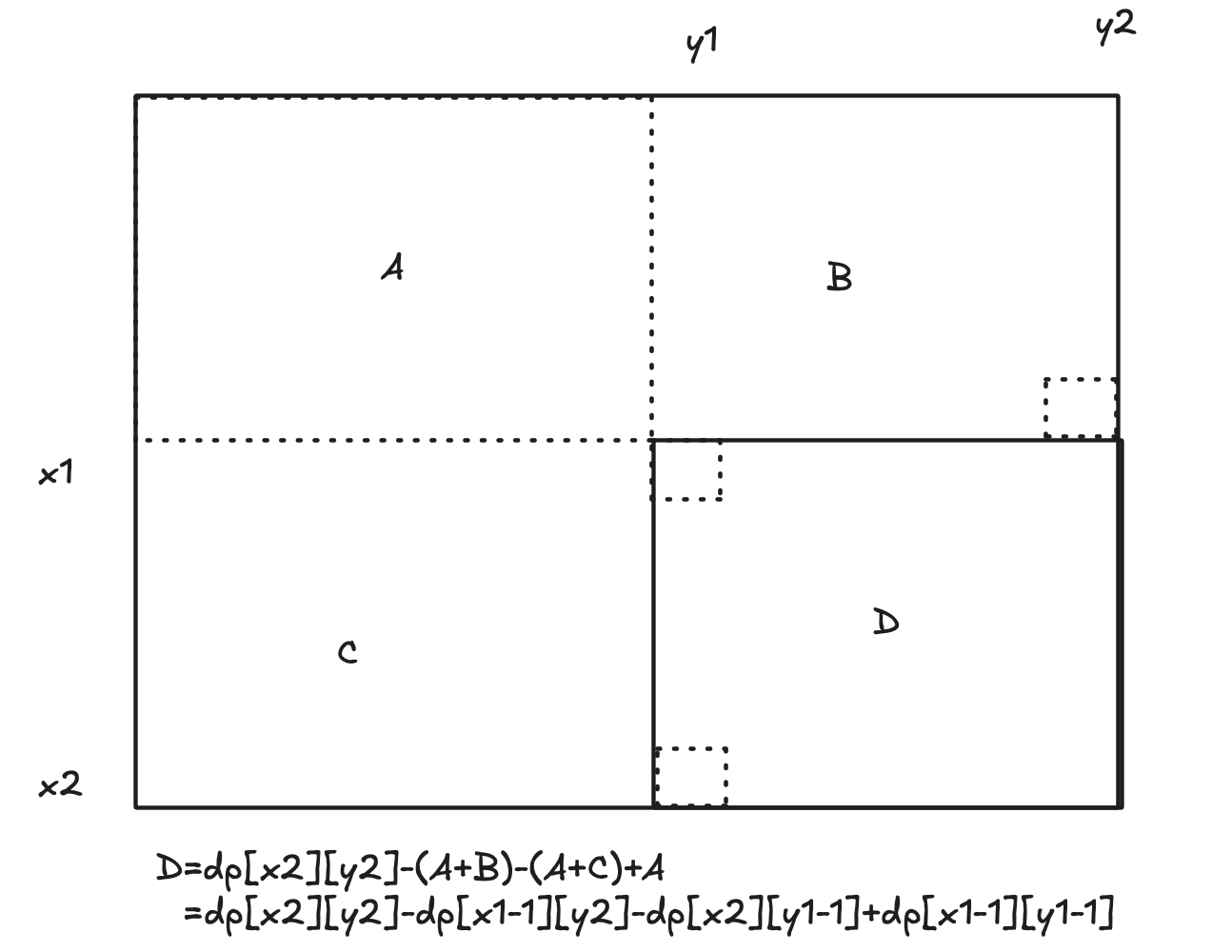
使用前缀和数组：

(x1,y1)到(x2,y2)矩阵中的元素之和：

---

代码及结果：

---

三、寻找数组的中心下标

题目链接：https://leetcode.cn/problems/find-pivot-index/

题目：

给你一个整数数组 nums，请计算数组的 中心下标。数组 中心下标 是数组的一个下标，其左侧所有元素相加的和等于右侧所有元素相加的和。

如果中心下标位于数组最左端，那么左侧数之和视为 0，因为在下标的左侧不存在元素。这一点对于中心下标位于数组最右端同样适用。
如果数组有多个中心下标，应该返回 最靠近左边 的那一个。如果数组不存在中心下标，返回 -1。
 

示例 1：
输入：nums = [1, 7, 3, 6, 5, 6]
输出：3
解释：
中心下标是 3 。
左侧数之和 sum = nums[0] + nums[1] + nums[2] = 1 + 7 + 3 = 11，
右侧数之和 sum = nums[4] + nums[5] = 5 + 6 = 11，二者相等。

 

示例 2：
输入：nums = [1, 2, 3]
输出：-1
解释：
数组中不存在满足此条件的中心下标。

 

示例 3：
输入：nums = [2, 1, -1]
输出：0
解释：
中心下标是 0 。
左侧数之和 sum = 0，（下标 0 左侧不存在元素），
右侧数之和 sum = nums[1] + nums[2] = 1 + -1 = 0。

---

思路：

本题的解题思路是 构建一个前缀和数组f和后缀和数组g，当下标为i时，判断f[i]和g[i]是否相等。

其中f[i]表示的是：[1,i]区间内所有元素之和。

f[i]=f[i-1]+arr[i]，f[0]=nums[0]；

g[i]表示的是：[i,n-1]区间内所有元素之和。

g[i]=g[i+1]-arr[i+1]，g[n-1]=nums[n-1]；

---

代码及结果：

class Solution {public int pivotIndex(int[] nums) {int n=nums.length;//预处理前缀和数组和后缀和数组int[]f=new int[n];int[]g=new int[n];f[0]=nums[0];g[n-1]=nums[n-1];for(int i=1;i<n;i++){f[i]=f[i-1]+nums[i];}for(int i=n-2;i>=0;i--){g[i]=g[i+1]+nums[i];}for(int i=0;i<n;i++){if(f[i]==g[i]){return i;}}return -1;}}

---

四、出自身以外数组的乘积

题目链接：https://leetcode.cn/problems/product-of-array-except-self/

题目：

给你一个整数数组 nums，返回数组 answer，其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积。

 

题目数据保证数组 nums 之中任意元素的全部前缀元素和后缀的乘积都在 32 位整数范围内。

 

请不要使用除法，且在 O(n) 时间复杂度内完成此题。

 

示例 1：
输入：nums = [1,2,3,4]
输出：[24,12,8,6]

 

示例 2：
输入：nums = [-1,1,0,-3,3]
输出：[0,0,9,0,0]

---

思路：

和上一题几乎一样，定义i下标的前缀积数组f[i]和后缀积数组g[i]。

f[i]表示的是：[0,i-1]区间内所有元素之积。

f[i]=f[i-1]*arr[i-1]，f[0]=1;

g[i]表示的是：[i+1,n-1]区间内所有元素之积。

g[i]=g[i+1]*arr[i+1]，g[n-1]=1;

---

代码及结果：

class Solution {public int[] productExceptSelf(int[] nums) {int n=nums.length;int []answer=new int[n];//预处理前缀积数组和后缀积数组int f[]=new int[n];int g[]=new int[n];f[0]=g[n-1]=1;for(int i=1;i<n;i++){f[i]=f[i-1]*nums[i-1];}for(int i=n-2;i>=0;i--){g[i]=g[i+1]*nums[i+1];}for(int i=0;i<n;i++){answer[i]=f[i]*g[i];}return answer;}}

---

五、和为k的子数组

题目链接：https://leetcode.cn/problems/subarray-sum-equals-k/

题目：

给你一个整数数组 nums 和一个整数 k，请你统计并返回该数组中和为 k 的子数组的个数。

 

子数组是数组中元素的连续非空序列。

 

示例 1：
输入：nums = [1,1,1], k = 2
输出：2

 

示例 2：
输入：nums = [1,2,3], k = 3
输出：2

---

思路：

这道题利用前缀和的思路解决，但不能使用之前讲解的滑动窗口算法，因为数组中元素不都大于0。

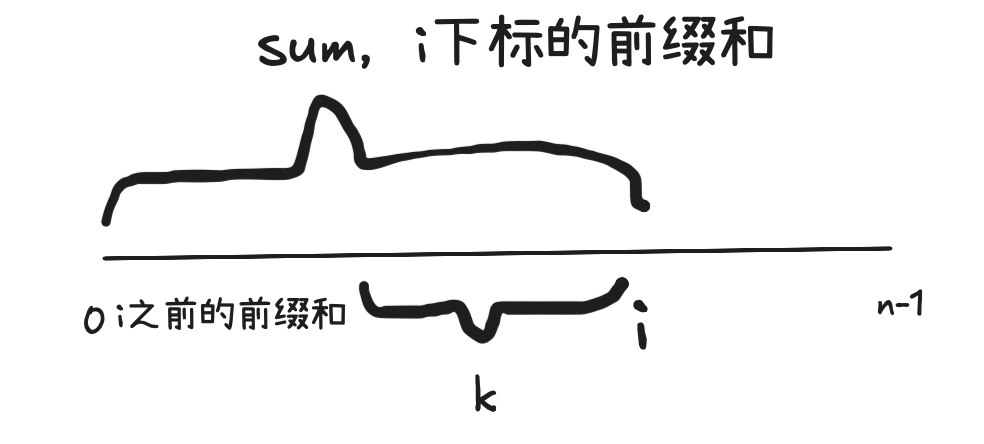
数组中有很多段，我们在遍历i的时候，只需查找有多少个以i结尾的子段为k即可。

使用前缀和的算法，就是查看在i之前，有多少前缀和为sum-k即可。

这道题中不用真的创建前缀和数组，而是将每一次i下标的前缀和sum放入hash表中即可。

❓有一个细节问题：

假设前缀和为 sum[i] 表示前 i 个元素的和。当 sum[i] = k时，这个子数组（从 0 到 i）本身就是一个有效的解。但代码中查找的是i之前存放的sum，hash 初始为空，这种情况会被漏掉。

---

代码及结果：

class Solution {public int subarraySum(int[] nums, int k) {Map<Integer,Integer> hash=new HashMap<>();int sum=0,ret=0;hash.put(0,1);for(int x:nums){sum+=x;ret+=hash.getOrDefault(sum-k,0);hash.put(sum,hash.getOrDefault(sum,0)+1);}return ret;}}

---

六、和可被k整除的子数组

题目链接：https://leetcode.cn/problems/subarray-sums-divisible-by-k/

题目：

给定一个整数数组 nums 和一个整数 k，返回其中元素之和可被 k 整除的非空子数组的数目。

 

子数组是数组中连续的部分。

 

示例 1：
输入：nums = [4,5,0,-2,-3,1], k = 5
输出：7
解释：
有 7 个子数组满足其元素之和可被 k = 5 整除：
[4, 5, 0, -2, -3, 1], [5], [5, 0], [5, 0, -2, -3], [0], [0, -2, -3], [-2, -3]

 

示例 2：
输入：nums = [5], k = 9
输出：0

---

思路：

同上一道题相似：

遍历i的时候，查找有多少i之前有多少x满足 （sum-x）%k==0

上面的式子可以转化为sum%k==x%k

我们每次将sum%k存入哈希表中。

---

代码及结果：

import java.util.*;
class Solution {public int subarraysDivByK(int[] nums, int k) {Map<Integer,Integer> hash1=new HashMap<>();int sum=0;//前缀和hash1.put(0%k,1);//前缀和的余数，出现的次数int num=0;for(int x:nums){sum+=x;int r=(sum%k+k)%k;num+=hash1.getOrDefault(r,0);hash1.put(r,hash1.getOrDefault(r,0)+1);}return num;}
}

---

七、连续数组

题目链接：https://leetcode.cn/problems/contiguous-array/

题目：

给定一个二进制数组 nums，找到含有相同数量的 0 和 1 的最长连续子数组，并返回该子数组的长度。

 

示例 1：
输入：nums = [0,1]
输出：2
说明：[0, 1] 是具有相同数量 0 和 1 的最长连续子数组。

 

示例 2：
输入：nums = [0,1,0]
输出：2
说明：[0, 1]（或 [1, 0]）是具有相同数量 0 和 1 的最长连续子数组。

 

示例 3：
输入：nums = [0,1,1,1,1,1,0,0,0]
输出：6
解释：[1,1,1,0,0,0] 是具有相同数量 0 和 1 的最长连续子数组。

---

思路：

这道题可以把0转换成-1，然后使用前缀和的算法解决，查找和为0的最长的连续子数组。

遍历i的时候，查找有多少i之前有多少x满足x==sum；

---

代码及结果：

class Solution {public int findMaxLength(int[] nums) {//转化：for(int i = 0; i < nums.length; i++) {if(nums[i] == 0) nums[i] = -1;}Map<Integer, Integer> hash = new HashMap<>();//储存的分别是前缀和，当前下标hash.put(0, -1); // 初始化，和为0的索引为-1int sum = 0, len = 0;//求和为0的最长子数组长度for(int i = 0; i < nums.length; i++) {sum += nums[i];if(hash.containsKey(sum)) {//有了sum就不需要再添加了int j = hash.get(sum);len = Math.max(len, i - j); // 计算长度时不需要+1} else {hash.put(sum, i);}}return len;
}
}

---

八、矩形区域和

题目链接：https://leetcode.cn/problems/matrix-block-sum/

题目：

给你一个 m x n 的矩阵 mat 和一个整数 k，请你返回一个矩阵 answer，其中每个 answer[i][j] 是所有满足下述条件的元素 mat[r][c] 的和：

 

• i - k <= r <= i + k，
• j - k <= c <= j + k 且
• (r, c) 在矩阵内。

 

示例 1：
输入：mat = [[1,2,3],[4,5,6],[7,8,9]], k = 1
输出：[[12,21,16],[27,45,33],[24,39,28]]

 

示例 2：
输入：mat = [[1,2,3],[4,5,6],[7,8,9]], k = 2
输出：[[45,45,45],[45,45,45],[45,45,45]]

---

思路：

这道题使用前缀和算法解决，

这道题主要就是求出以[i][j]为原点，k为半径的区域元素之和，下面总结了边界情况：

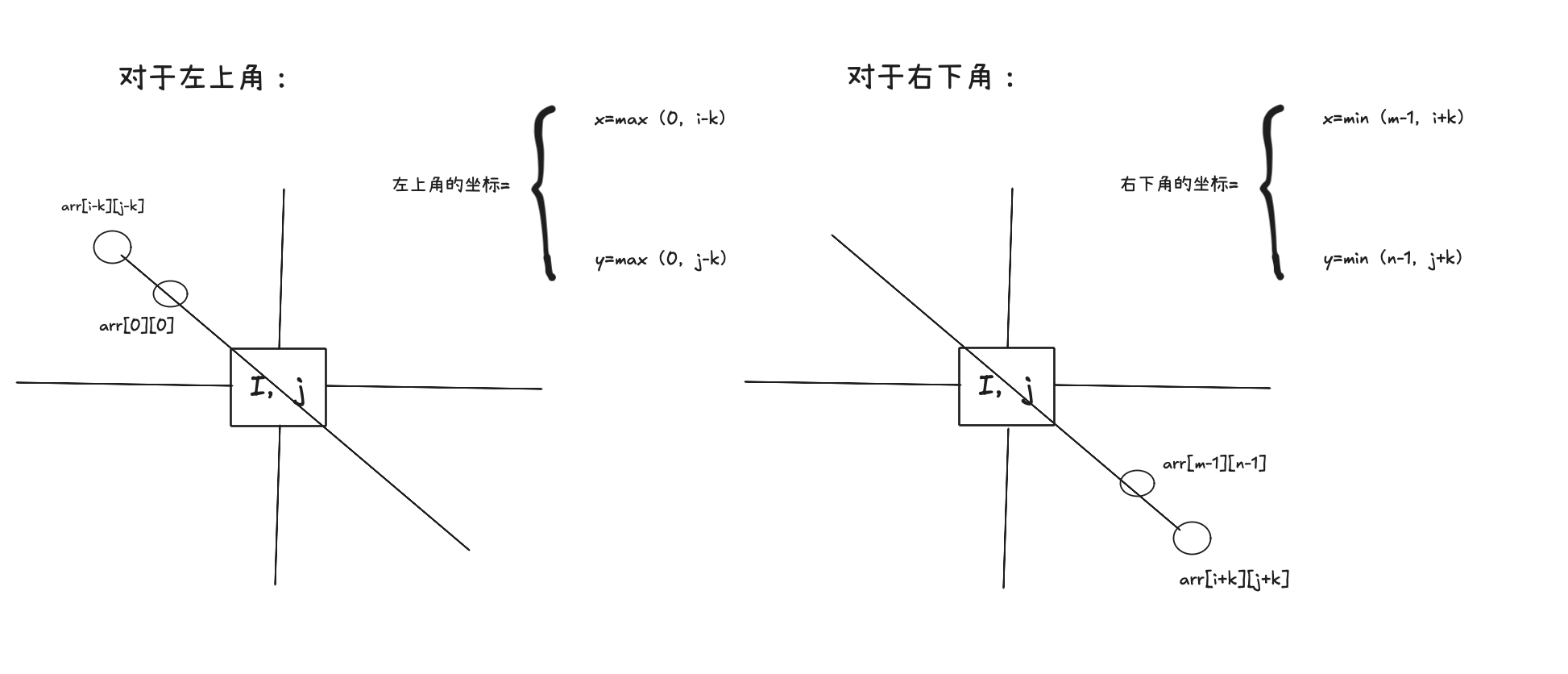
然后创建二维前缀和数组dp

二维前缀和数组dp是从1下标开始放入元素的，dp对应到原数组的下标 是要-1的。

---

代码及结果：

class Solution {public int[][] matrixBlockSum(int[][] mat, int k) {int m= mat.length,n=mat[0].length;//创立前缀和矩阵int dp[][]=new int[m+1][n+1];for(int i=1;i<m+1;i++){for(int j=1;j<n+1;j++){dp[i][j]=dp[i-1][j]+dp[i][j-1]-dp[i-1][j-1]+mat[i-1][j-1];//这里的mat[i][j]要变成mat[i-1][j-1]//因为dp是在1位置开始的，总是比mat数组要后一位，mat总是在他的前一位，dp对应的mat下标-1}}//使用前缀和矩阵int answer[][]=new int[m][n];for(int i=0;i<m;i++){for(int j=0;j<n;j++){int x1=Math.max(0,i-k)+1;//answer数组是从0开始的，dp数组是从1开始的，ansewr对应的dp下标+1int y1=Math.max(0,j-k)+1;int x2=Math.min(m-1,i+k)+1;int y2=Math.min(n-1,j+k)+1;answer[i][j]=dp[x2][y2]-dp[x1-1][y2]-dp[x2][y1-1]+dp[x1-1][y1-1];}}return answer;}}

---