当前位置：首页 > news >正文

元启发式算法分类

news 2025/9/20 15:21:41

0.引言

最近讲了很多元启发式算法，但是没有一个目录或者指南，无法为每个算法归类，今天写一篇类似综述的文章，为这些算法分一下类。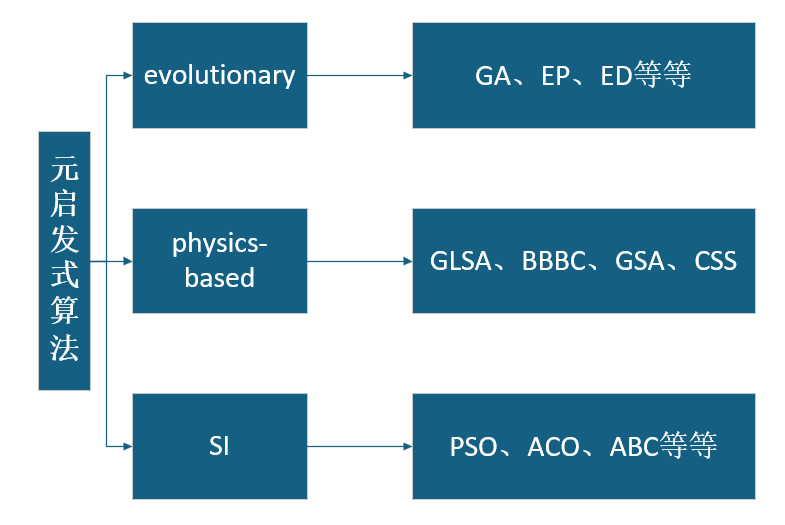

元启发式算法可分为三大类：进化算法（evolutionary）、基于物理算法（physics-based）和 SI 算法（SI algorithms）。依次讲解一下。

1.进化算法（evolutionary，EA）

进化算法是一类受生物进化启发的优化算法，属于计算智能领域。它模拟自然选择、遗传变异等机制，通过迭代搜索解决复杂优化问题。核心思想是通过种群中个体的适应度评估、选择、交叉和变异，逐步逼近最优解。

这些算法共享一个共同的框架：维持一个候选解种群，通过模拟自然选择、变异、重组等操作，使种群不断进化，从而逼近问题的最优解。 它们的核心区别在于如何表示解（编码方式）以及如何进行选择和变异。

遗传算法(Evolutionary Algorithms)GA——由John Holland及其学生发展，是最早、影响最广泛的进化算法。它的灵感直接来源于孟德尔的遗传学，强调“染色体”的交叉重组。

表示：最初使用二进制编码（0和1的字符串）来表示解，就像生物体的染色体。现在也广泛使用其他编码方式。

操作：交叉是核心操作，被认为是推动进化的主要动力。通过交换两个父代个体的部分“基因”来产生新个体。突变作为辅助操作，用于引入和维持多样性。

选择：常用轮盘赌选择（按适应度比例分配选中概率）或锦标赛选择。

进化规划(Evolutionary Programming)EP——由 Lawrence J. Fogel 在20世纪60年代提出，最初用于模拟智能行为（如预测有限状态机）。现代EP更专注于数值优化。像一群探险家，各自独立地在自己周围随机探索，然后大家比一比谁找到的地方更好，好的留下继续探索。

表示：直接使用实数值向量表示解，非常适合连续优化问题。

操作：没有交叉（重组）操作。进化完全依赖于突变。

选择：采用锦标赛选择。每个解与随机选出的其他多个解进行比较，根据其适应度（优劣程度）排名，选择排名高的个体进入下一代。

自适应变异：通常变异步长（突变的大小）会与解一起进化，从而实现自适应的搜索（开始时大步长全局探索，后期小步长局部精细搜索）。

差分进化(Differential Evolution)ED——由 Storn 和 Price 提出，是一种非常强大且流行的实参数优化算法，以其简单、高效、鲁棒性强而著称。探险家们不仅自己探索，还互相交流信息：“我从A点出发，朝着B和C之间的方向走了一段，发现了一个可能更好的地方，我去试试，如果真的好就换过去。”

表示：实数值向量。

核心操作： 差分变异 和交叉。

差分变异：新候选解通过对种群中随机选取的几个解进行向量差分运算来生成。例如：试验向量 = A + F * (B - C)，其中A, B, C是随机个体，F是缩放因子。

交叉：将突变生成的试验向量与原来的目标向量按一定概率进行混合，生成最终的子代。

选择： 贪婪选择。子代只有比父代更优秀时才会替换父代进入下一代，否则父代保留。这保证了种群的质量单调不下降。

进化策略(Evolution Strategies)ES——由 Ingo Rechenberg 和 Hans-Paul Schwefel 在德国发展起来，最初用于解决流体动力学等工程优化问题。极其擅长数值优化。一队专业的测绘人员。他们不仅记录自己的位置（解），还精密地控制和调整自己每一步的步长和方向（策略参数），并且有严格的团队更替规则（选择策略）。

表示：实数值向量。其关键创新在于同时进化解和策略参数（如变异步长σ和相关系数）。

操作：主要依赖重组和突变。重组方式多样（离散/中间值重组）。突变是核心，通常使用高斯分布扰动，并伴有自适应的步长。

选择：著名的 （μ, λ）- ES 或 （μ + λ）- ES 策略。

μ 表示父代数量，λ 表示子代数量。

（μ, λ）：只从λ个子代中选择最好的μ个作为下一代的父代（只能单代竞争）。

（μ+λ）：从父代和子代（μ+λ）中一起选择最好的μ个（两代竞争）。

遗传编程 (Genetic Programming)GP—— 由 John Koza 推广，是遗传算法（GA）的延伸。它的目标不是找到一个固定的解，而是进化出一个计算机程序或模型来解决任务。不是进化一个参数，而是进化一个“配方”或“方法”。就像通过随机组合和修改菜谱中的食材和步骤，最终进化出一道美味佳肴（能解决问题的程序）。

表示：解是计算机程序，通常用树形结构表示（例如，语法树、函数表达式、决策树等）。

操作：采用与GA类似的交叉和突变，但操作对象是树。

交叉：交换两棵树的分支（子树）。

突变：随机改变树上的一个节点（操作符或操作数）或用新子树替换一个分支。

选择：通常采用GA中的选择方式，如轮盘赌选择、锦标赛选择等。

生物地理学优化(Biogeography-Based Optimization)BBO——由 Dan Simon 提出，灵感来源于物种在栖息地之间的迁移和分布。栖息地的适宜度指数 (HSI) 类比为解的适应度，特征（SIV）类比为解的参数。

表示：实数值向量，每个解被称为一个“栖息地”。

核心操作：迁移和突变。

迁移：类似于交叉，但具有概率性。高HSI（优质）栖息地的特征（SIV）会倾向于迁移到低HSI（劣质）栖息地中，共享优良特性。反之，劣质栖息地也会接收优质特征。

突变：栖息地的物种数量变化率决定了突变概率。低概率和高概率的物种数量的栖息地更容易发生突变，从而增加多样性。

选择：算法本身通过迁移操作隐含了选择，优良解的信息被保留和传播。

2.基于物理的算法（physics-based）

元启发式的第二个主要分支是基于物理的技术。这种优化算法通常模仿物理规则。

这些算法的机制与 EA 不同，因为一组随机的搜索代理根据物理规则在整个搜索空间中进行通信和移动。例如，使用重力、射线投射、电磁力、惯性力、重量等来实现这种运动。

这类算法中包含了很多经典算法：引力局部搜索（GLSA），大爆炸大紧缩（BBBC），引力搜索算法（GSA），带电系统搜索（CSS），中心力优化（CFO），人工化学反应优化算法（ACROA），黑洞（BH）算法，射线优化（RO）算法，小世界优化算法（SWOA），基于星系的搜索算法（GbSA），弯曲空间优化（CSO）等等等等。这里简要介绍BBBC算法和GSA算法。

引力搜索算法 (Gravitational Search Algorithm)——由Esmat Rashedi等人于2009年提出。其灵感来源于牛顿的万有引力定律。在GSA中，解空间中的每个候选解被看作一个具有质量的“物体”。物体的“质量”由它的适应度值（解决问题的能力）决定：解越好，质量越大。就像太阳系中，所有行星都被质量巨大的太阳（当前找到的最佳解）的引力所束缚，并围绕着它运行。质量小的天体（较差解）更容易被拉向质量大的天体。

协作搜索：种群中的个体通过“引力”相互交流和引导，优秀的个体（质量大）会对整个种群的移动方向产生主导性影响。

自适应：随着迭代进行，优质解的质量会越来越大，其吸引力也越强，从而在搜索后期促使种群快速收敛到最优区域。

平衡探索与开发：初期引力常数较大，鼓励全局探索（探索）；后期引力常数减小，利于局部精细搜索（开发）。

大爆炸大挤压算法 (Big Bang-Big Crunch Algorithm)——由Erol和Eksin在2006年提出。其灵感来源于宇宙起源的“大爆炸”和收缩的“大挤压”理论。算法交替执行两个阶段：大爆炸 (Big Bang) 阶段：一个无序的、随机的能量释放过程，对应于生成随机解（探索）；大挤压 (Big Crunch) 阶段：一个将物质和能量向内收缩到一个点的过程，对应于将所有当前解的信息聚合到一个中心点（开发）。就像宇宙的一次次呼吸：先吸气（将所有物质和信息收缩到一个中心点），再呼气（从中心点向周围喷发出新的物质去探索），如此循环往复，每次呼吸都更接近宇宙的核心。

两阶段循环：结构非常简单清晰，只有爆炸和挤压两个交替的步骤。

信息聚合：通过计算质心，有效地利用了整个种群的信息来指导下一次搜索。

收敛性强：由于每次迭代都围绕质心进行，算法通常具有很好的收敛速度。

3.群体智能算法(SI)

这些算法大多模仿自然界中生物群、牛群、羊群或成群的社会行为。该机制几乎类似于基于物理的算法，但搜索代理使用生物的模拟集体和社会智能进行导航。除了广为人知的PSO算法，ACO算法,ABC算法之外还有2001年蜜蜂优化算法（MBO），2003 年的人工鱼群算法（AFSA），2005 年的白蚁算法，2007 年的黄蜂群算法，2007 年的猴子搜索，2008年蜜蜂采集花粉算法（BCPA），2009 年的杜鹃搜索（CS），2009 年的海豚伙伴优化（DPO），2010 年的萤火虫算法，2012 年的鸟类交配优化器（BMO），蝙蝠算法（BA），灰狼寻优算法（GWO），白鲸算法等等等等.

群体智能的核心灵感来源于社会性生物群体（如蚁群、鸟群、鱼群、蜂群）的集体行为。这些群体中的个体行为非常简单，也没有中央控制，但通过个体之间的简单规则和局部交互，整个群体能够呈现出高度结构化、智能化的协同行为，解决复杂问题（如觅食、筑巢、迁徙）。

粒子群优化算法 (Particle Swarm Optimization)——鸟群或鱼群的运动模拟。鸟群在飞行中突然改变方向、散开、聚集，其行为非常协调。
1. 每个候选解是搜索空间中的一个“粒子”。
2. 每个粒子根据自己的历史最佳位置（pBest） 和整个种群的历史最佳位置（gBest） 来调整自己的飞行速度和方向。
3. 粒子通过追踪这两个极值来不断更新自己的位置，最终整个种群趋于最优解。