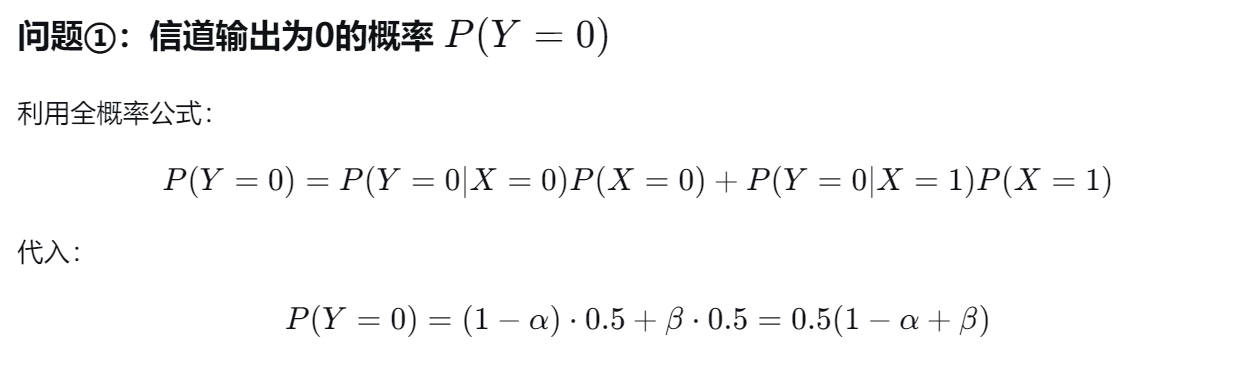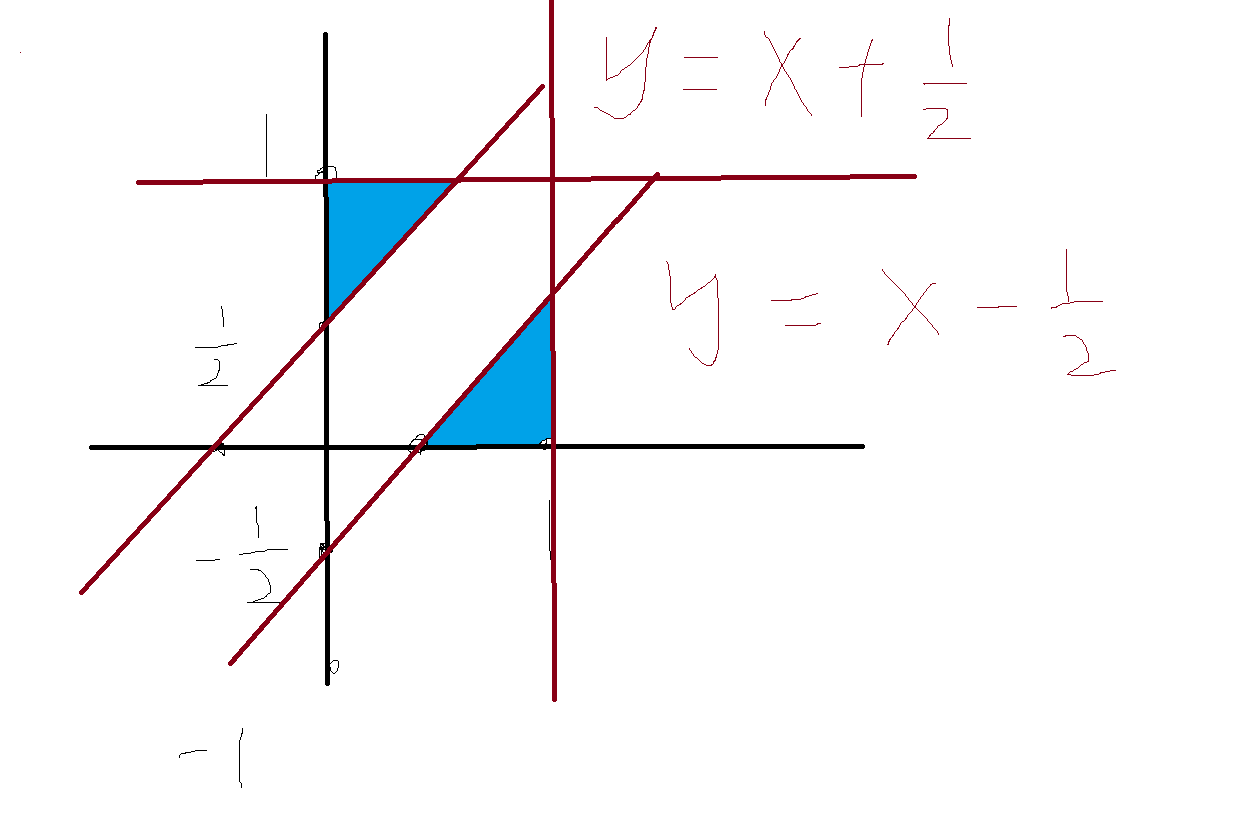随机过程笔记
概率空间和随机对象
概率空间
Borel集
样本空间的某些子集组成的一个集合,记作
。若
满足:
称是定义在样本空间
上的
集。
例子:
样本空间
:
{1, 2, 3, 4, 5, 6}一个
:
{ Ø, S, {1}, {2, 3, 4, 5, 6} }Ø代表空集。S代表整个样本空间。{1}代表一个事件(抛出1点)。{2, 3, 4, 5, 6}代表事件{1}的补集(抛出不是1的点)。
验证它是否是Borel事件集:
包含全集和空集:
S和Ø都在里面。 ✅对补集封闭:
{1}的补集是{2,3,4,5,6},它在集合里。 ✅{2,3,4,5,6}的补集是{1},它在集合里。 ✅S的补集是Ø,它在集合里。 ✅Ø的补集是S,它在集合里。 ✅
对可数并封闭:
任意取集合里的事件做并集,结果都仍然在这个集合里。
例如:
{1} ∪ Ø = {1}✅{1} ∪ {2,3,4,5,6} = S✅{1} ∪ S = S✅...所有可能组合都满足。
验证通过,{ Ø, S, {1}, {2, 3, 4, 5, 6} } 是一个合法的Borel事件集。
最小Borel事件集:
样本空间
:
{1, 2, 3, 4, 5, 6}:
{ Ø, S }这是最小的Borel事件集,永远成立。
只包含必然事件和不可能事件。
最大Borel事件集:
样本空间
:
{1, 2, 3, 4, 5, 6}:
P(S),即的所有子集的集合。
例如,
{1},{2},{1,2},{1,3,5},{2,4,6}等等,所有64个可能的子集都是这个σ代数的元素。这是最大的Borel事件集。
概率集函数
若
,且
则
若
, 则
条件概率的定义
独立性
若,称事件
相互独立。
若
独立性与互斥性
独立表示没有关系,而互斥是一种对立关系,即发生则
不能发生,
对
是有影响的,反之亦然。所以互斥事件一定不独立。独立事件一定不互斥。
全概率公式
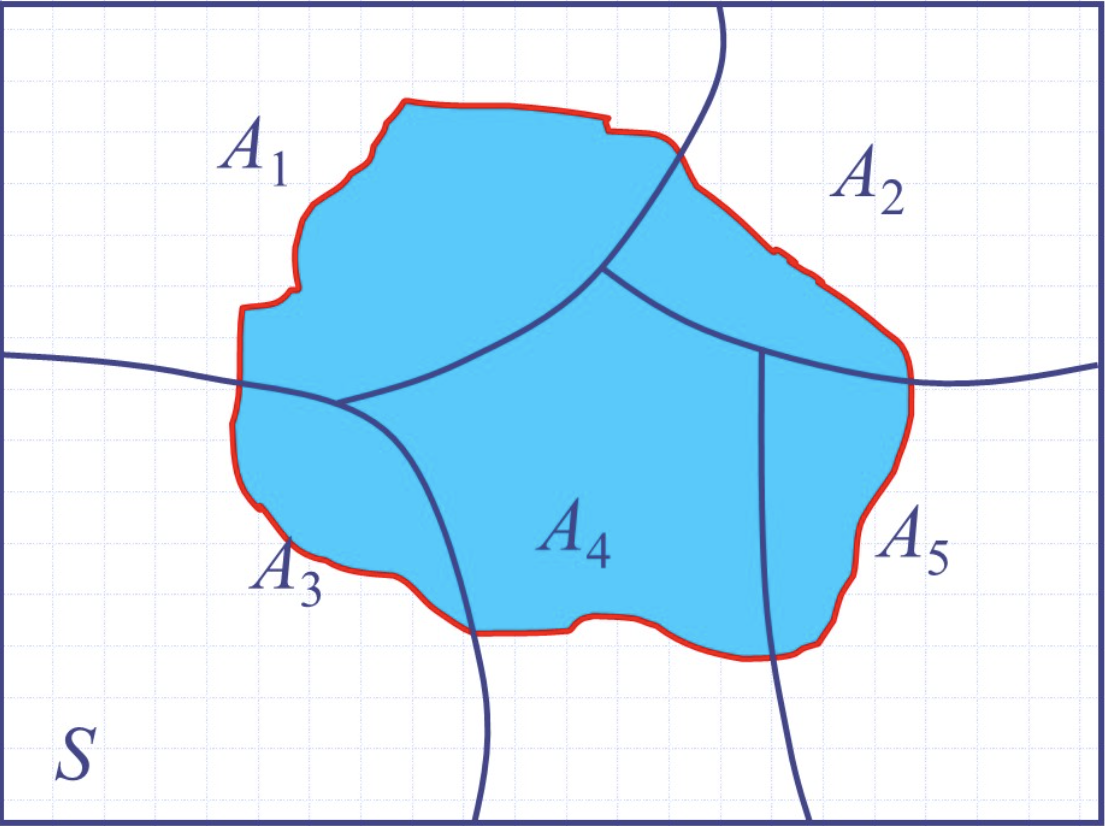
在连续条件下的推广:
贝叶斯公式
:后验概率
:先验概率
随机变量
随机对象
当样本空间为一维实数集合时,则称该一维实变量为随机变量。
当样本空间为高维实数空间时,则称该高维实数变量为随机向量。
当样本空间为定义于某个数集上的函数组成,则称该函数集合为随机过程。
概率质量函数
任何一种离散型随机变量都可以统一地用概率质量函数表示。
其他事件的概率通过概率质量函数计算得到
连续型随机变量不可以用概率质量函数表示
概率生成函数
设随机变量的取值和概率分别为
,则
X的概率生成函数为
展开生成函数:
求一阶导数:
现在,令 ,所有包含
的项都变为 0:
求 k 阶导数:
z = 0代入:
例子泊松分布
概率生成函数:
用生成函数求概率:
求 :
得到:
概率分布函数
单调递增,若
,则
右连续,即
概率密度函数
对任意实数
概率特征函数
设
则
例子:
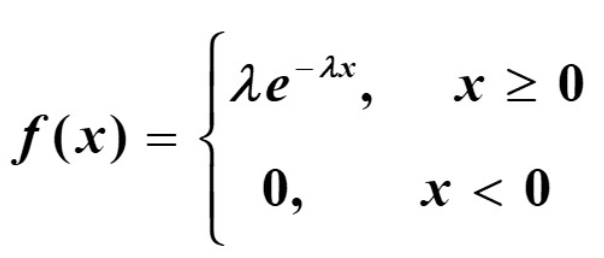
分布函数:
当时:
当 时:
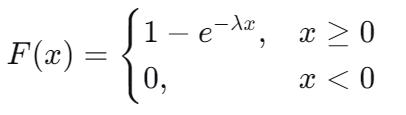
特征函数:
当:
,复指数的模始终为1
当:
因此:
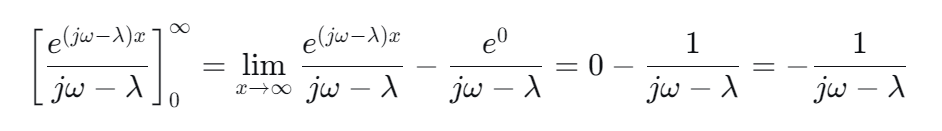
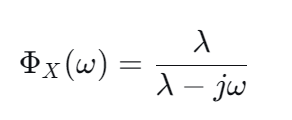
作业
2025.9.19
2.5

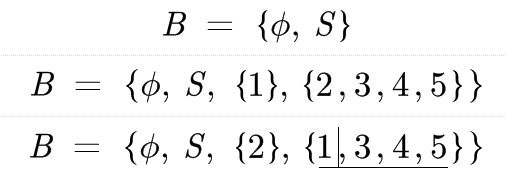
2.10
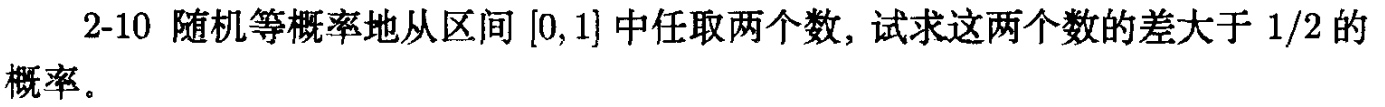
四分之一
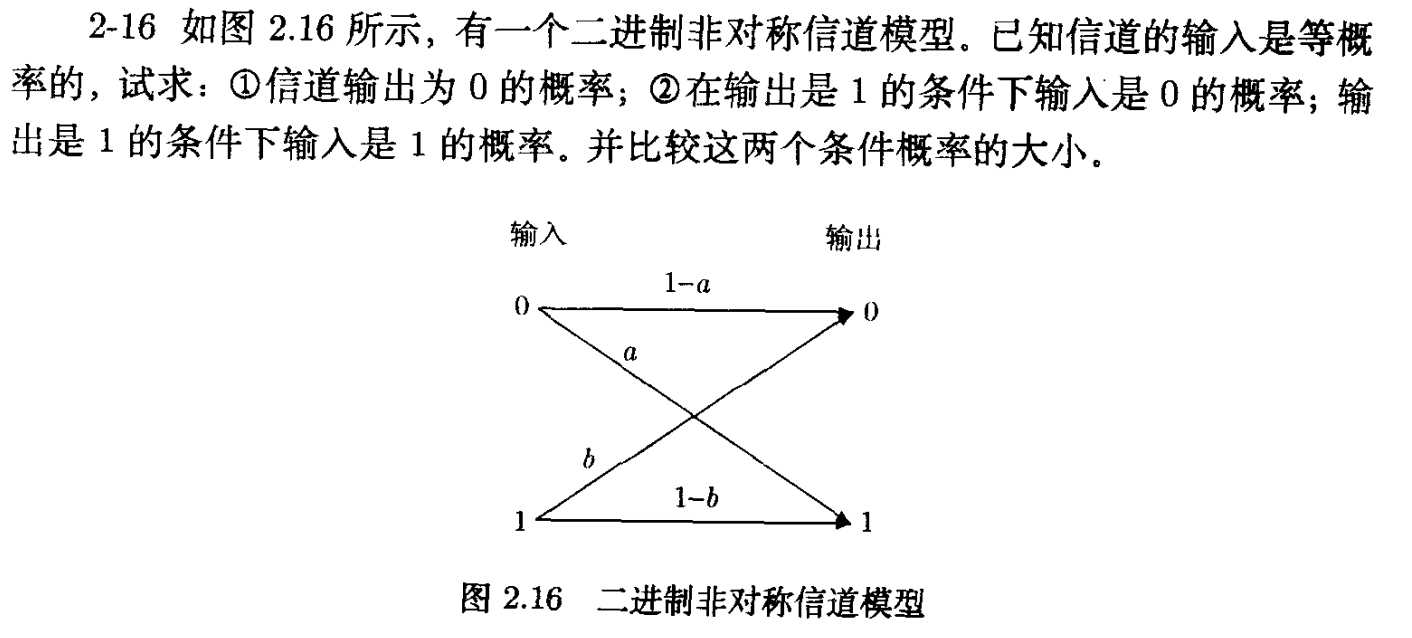
2.16