刷题记录（10）stack和queue的简单应用
一、最小栈
155. 最小栈 - 力扣（LeetCode）
怎么说呢，其实push pop top直接套STL库的就行，其实最麻烦的就是如何获得堆栈中最小的元素（而且硬性要求常数时间解决），毕竟我们非常清楚，栈是不能随意访问元素的，至多只能访问栈顶元素。
其实在打这句话的时候我就想到了一个解决方法，虽然我们不能随意的访问元素，但是push的时候我们可以接触到每个元素，只要记录下来最小的不就完了：
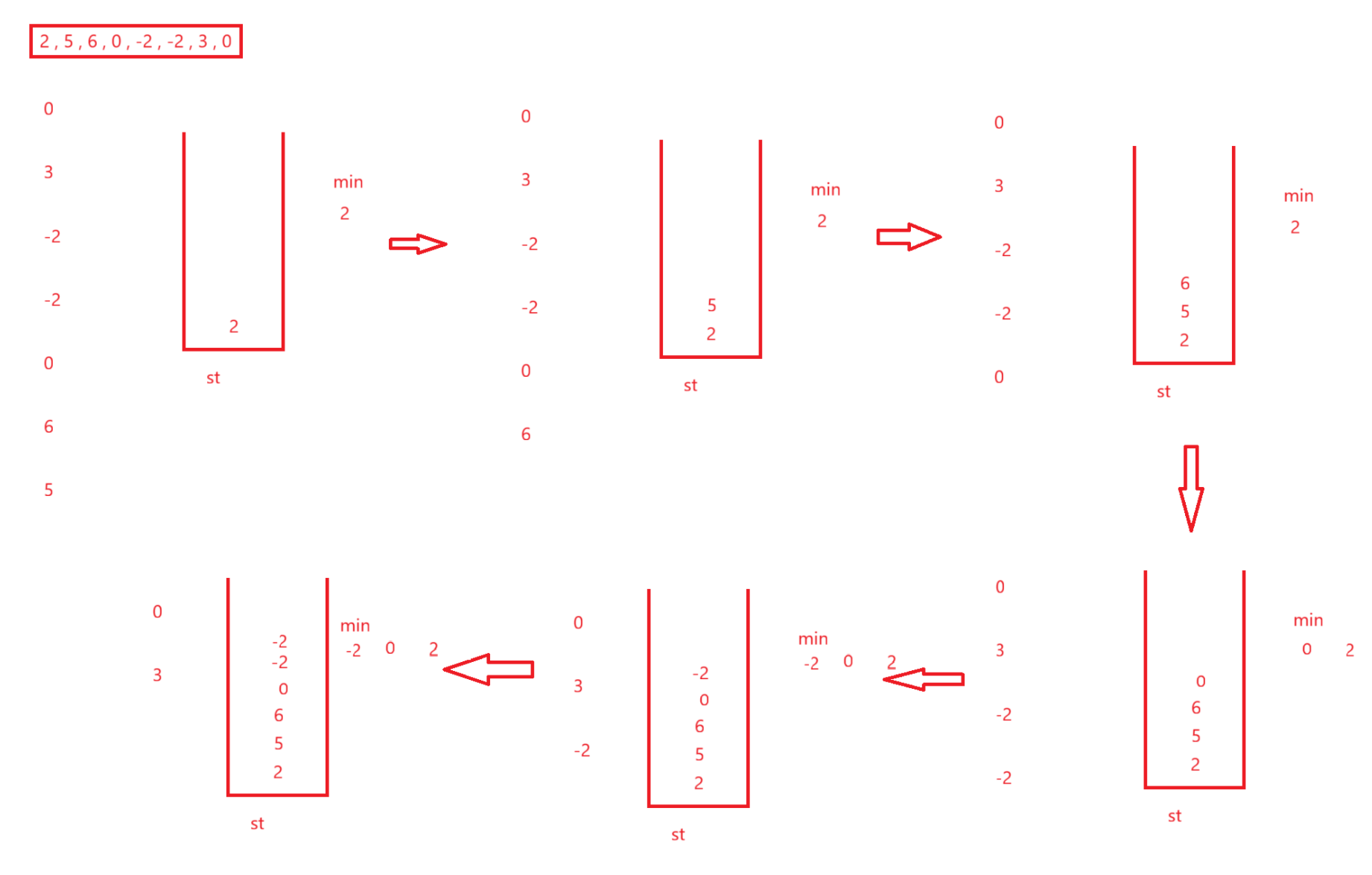
但是画着画着就出现问题了，如果在目前这一步连续pop两次，也就是把-2全部pop出去，那你栈里最小不就变0了嘛，这个时候你的min受影响的啊，也就是pop以后也必须检查并修改min的值。
于是，再来一个栈：
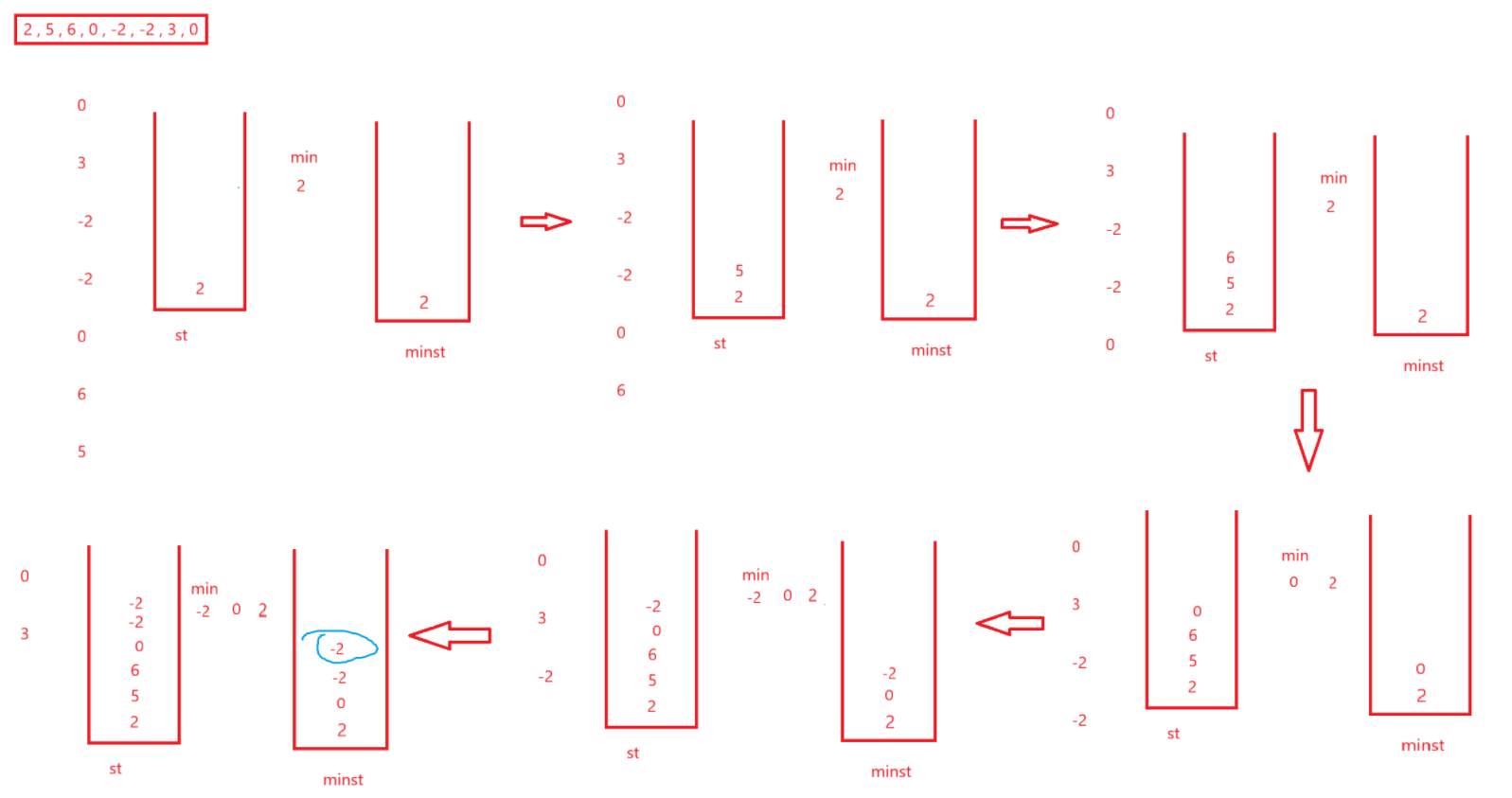
需要注意的点就是如果检测到minst的栈顶和此次push进st的值一样我们也得push到minst里。
其实是倒过来推的，如果st需要pop-2，我们为了维护最小值，肯定得检测检测minst栈顶和它相等不等，相等也得pop，所以就得出来如果此次往st中push的值跟minst的top相等，也得push到minst里。
class MinStack {
public:MinStack() {}void push(int val) {st.push(val);if(minst.empty())minst.push(val);else if(val <= minst.top())minst.push(val);}void pop() {if(minst.top() == st.top())minst.pop();st.pop();}int top() {return st.top();}int getMin() {return minst.top();}
private:stack<int> st;stack<int> minst;
};直接通过了，需要说的是默认构造函数，我们说过，所有非静态成员变量一定走初始化列表，那么我们两个成员栈也都需要走初始化列表，我们还说过：
①初始化列表给值的以初始化列表的值初始化
②初始化列表没给值有缺省值的按缺省值走初始化列表
③走不了初始化列表初始化的，编译器对于内置类型的初始化可能是随机值也可能是0之类的值；对于自定义类型调用它们的默认构造函数，没有默认构造的报错
好了好了，不用背书了，所以这里我们的默认构造啥都没写就是这个道理，没有显式初始化的走自定义类型的默认构造。
这道题的重点就是从存到一个变量min里转变到存到一个栈里预防pop造成的负面效果。
二、栈的压入、弹出序列
栈的压入、弹出序列_牛客题霸_牛客网
等于给你两个序列，一个序列代表压栈顺序，一个序列代表出栈顺序，让你判断出栈序列合理不合理。
这道题其实有点像思路实现，我自己想的昂，毕竟咱们人碰见这个题咋做，就说这个序列：
看见第一个出的是4，所以入的时候肯定是1234入进去了，出了个4，然后发现下一个是5，那就入5出5，再连着出刚好就是这个序列。
参数不是这俩嘛。
可以设计一个栈，让它入到popV的第一个数再停，然后开始遍历popV，每次比较栈顶元素是否和popV此次遍历的数相同，如果不相同，先看看push完了没，没有push完就疯狂的push直到碰见popV遍历到的数。如果相同直接pop再继续检查下一个应该pop的值。
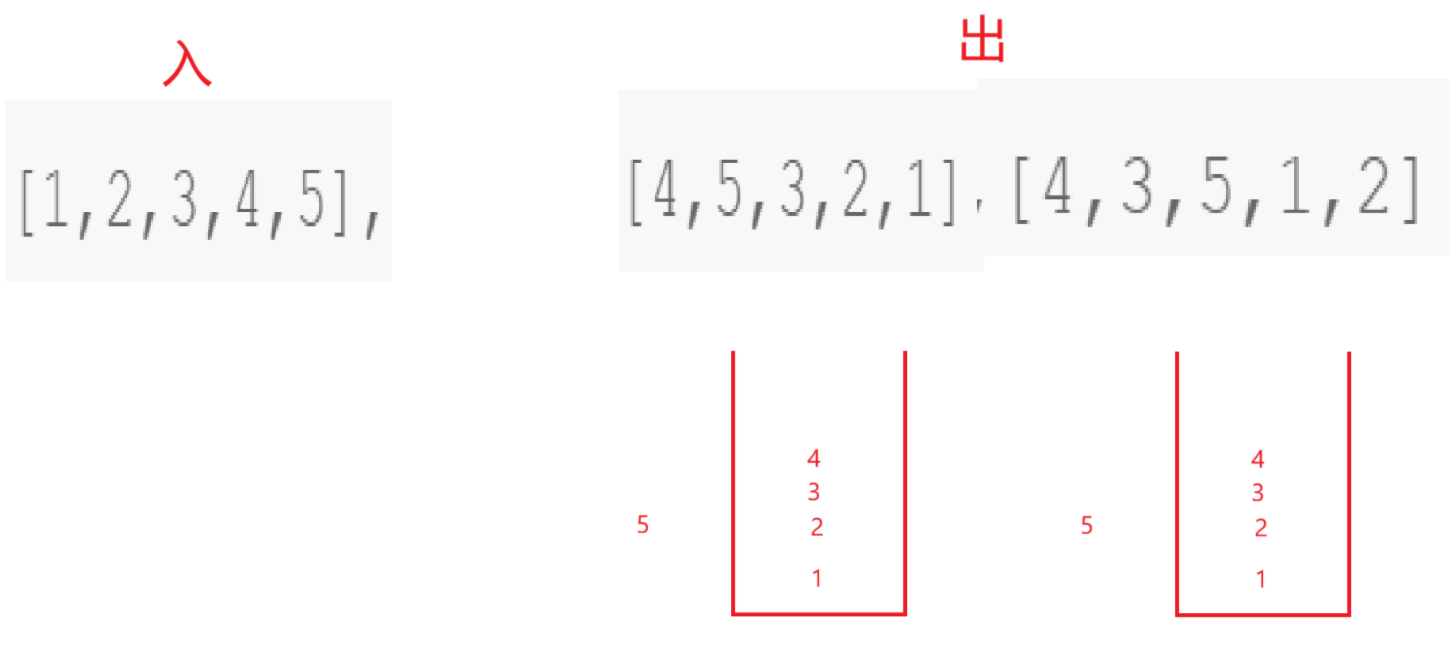
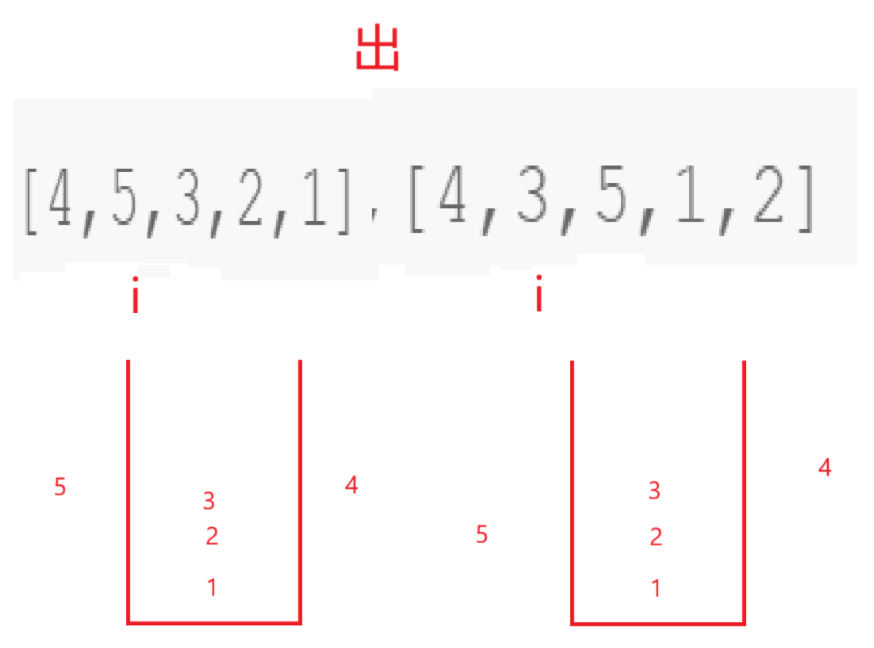
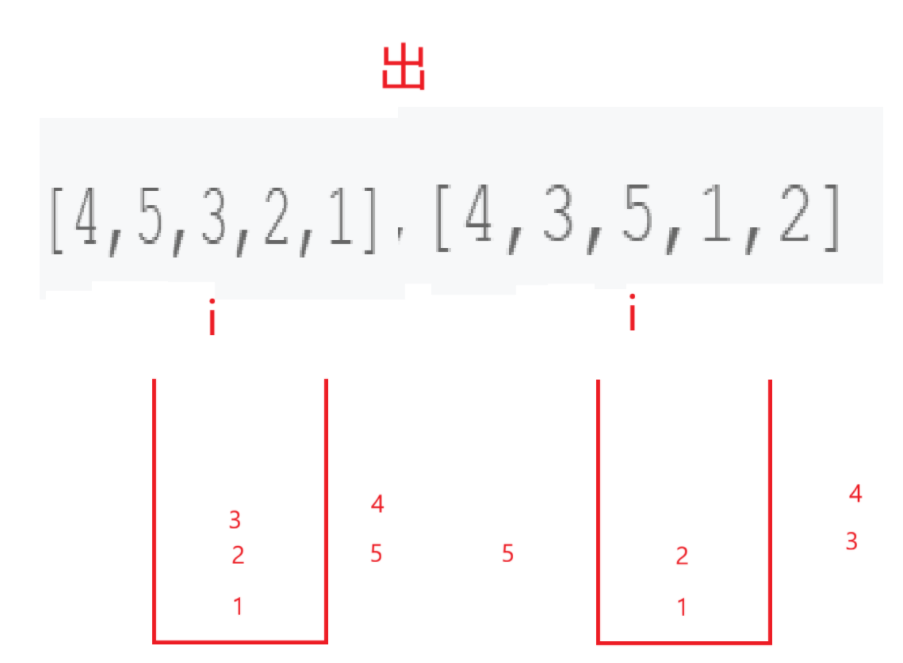
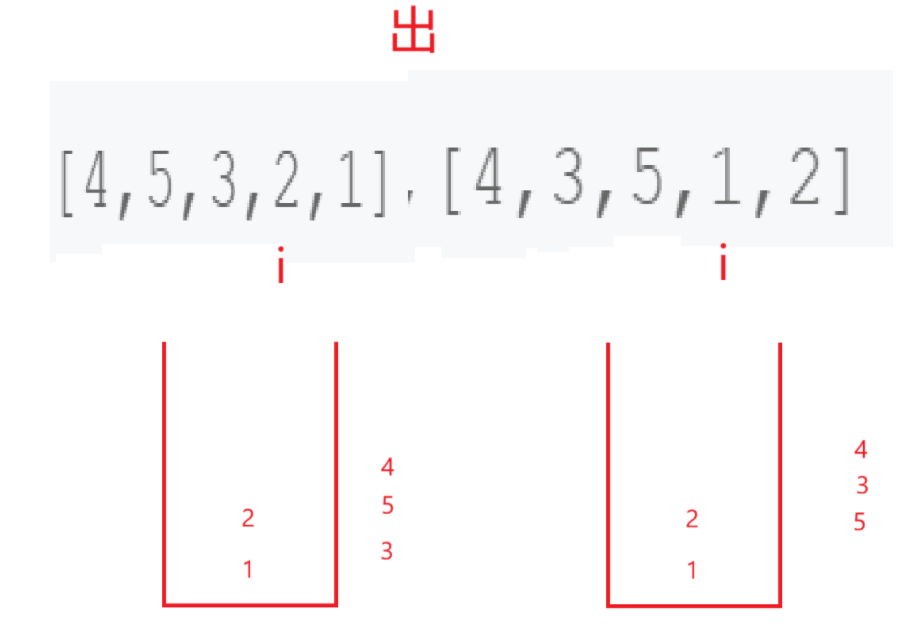
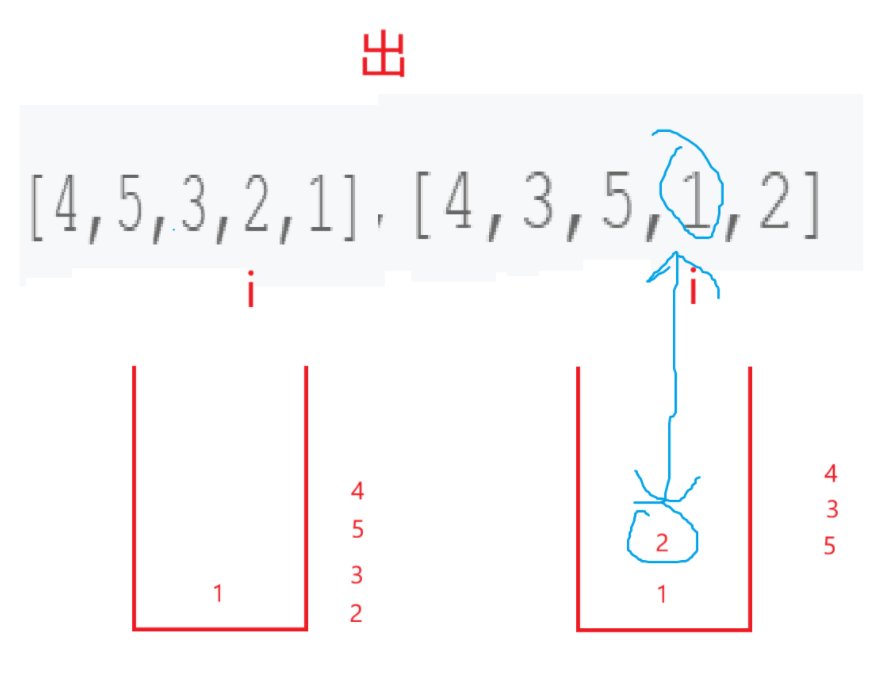
到这就不用再演示了。
但是看题目的意思估计俩序列里的数不会不一样，顶多次序不合理，先不考虑俩序列不一样吧，那以上就是我们全部的思路，其实说思路，也就是把我们做选择题的做法转换成一句句代码表达出来。
序列不合理就是遍历的时候遍历到不一样的。
序列合理就是遍历完了也没出事的。
代码出现过两个问题：
class Solution {
public:/*** 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可*** @param pushV int整型vector* @param popV int整型vector* @return bool布尔型*/bool IsPopOrder(vector<int>& pushV, vector<int>& popV) {// write code herestack<int> st;st.push(pushV[0]);//先push到与popV[0]相同 size_t i = 1;while (i <= pushV.size() && st.top() != popV[0])st.push(pushV[i++]);//遍历popV check st.top() ? popV[j]//== pop; j++//!= check i ? pushV.size()->push完毕false,未push完毕,while pushsize_t j = 0;while (j < popV.size()){if (st.top() == popV[j++])st.pop();else if (i < pushV.size())while (i <= pushV.size()&& st.top() != popV[j])st.push(pushV[i++]);elsereturn false;}return true;}
};第一次发现的错误点在：
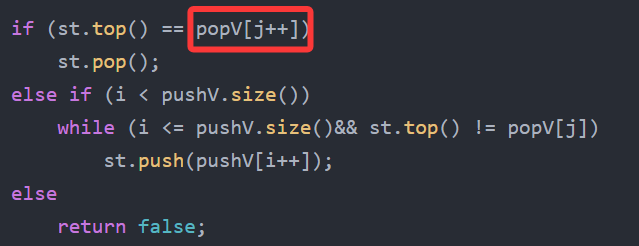
只要进循环就得判断条件，把++写到判断条件可能造成：
j遍历到5了，很明显按说该走第二个条件，但是第一个条件判断完以后j就变成指向3的了，直接死翘翘了。
第二次错误点就是，我在刚创建好st就先push就是怕栈空，结果到while里就不管了，第一个if赤裸裸直接st.top()，第二个else if也差不多没遍历完的往里进里层的while也是不管栈空不空，直接往上st.top()。
除此之外就只是我们正常做选择的正常思路。
三、用两个栈实现队列
232. 用栈实现队列 - 力扣（LeetCode）
文艺复兴昂，只不过是以C++的形式，今非昔比了。
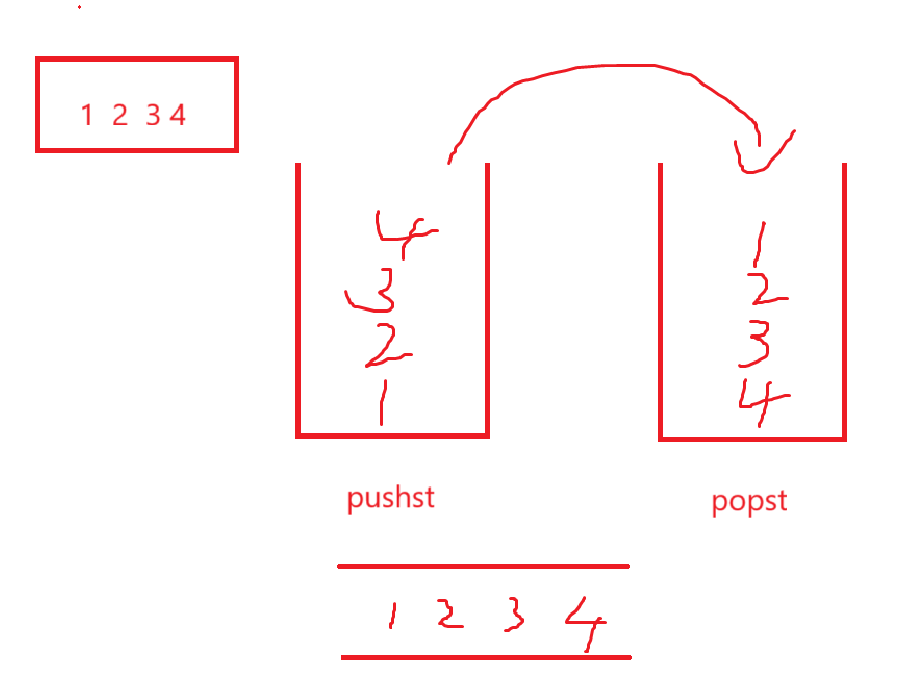
一个栈用来压数据，如果调pop或者peek（front）接口，那就把pushst依次全部入到popst，至于empty，俩栈都不为空队列就不为空。
class MyQueue {
public:MyQueue() {}void push(int x) {pushst.push(x);}int pop() {int ret;if(!popst.empty()){ret = popst.top();popst.pop();}else{while(!pushst.empty()){popst.push(pushst.top());pushst.pop();}ret = popst.top();popst.pop();}return ret;}int peek() {if(!popst.empty())return popst.top();else{while(!pushst.empty()){popst.push(pushst.top());pushst.pop();}return popst.top();}}bool empty() {return pushst.empty()&&popst.empty();}
private:stack<int> pushst;stack<int> popst;
};需要强调的就是如果popst不为空的话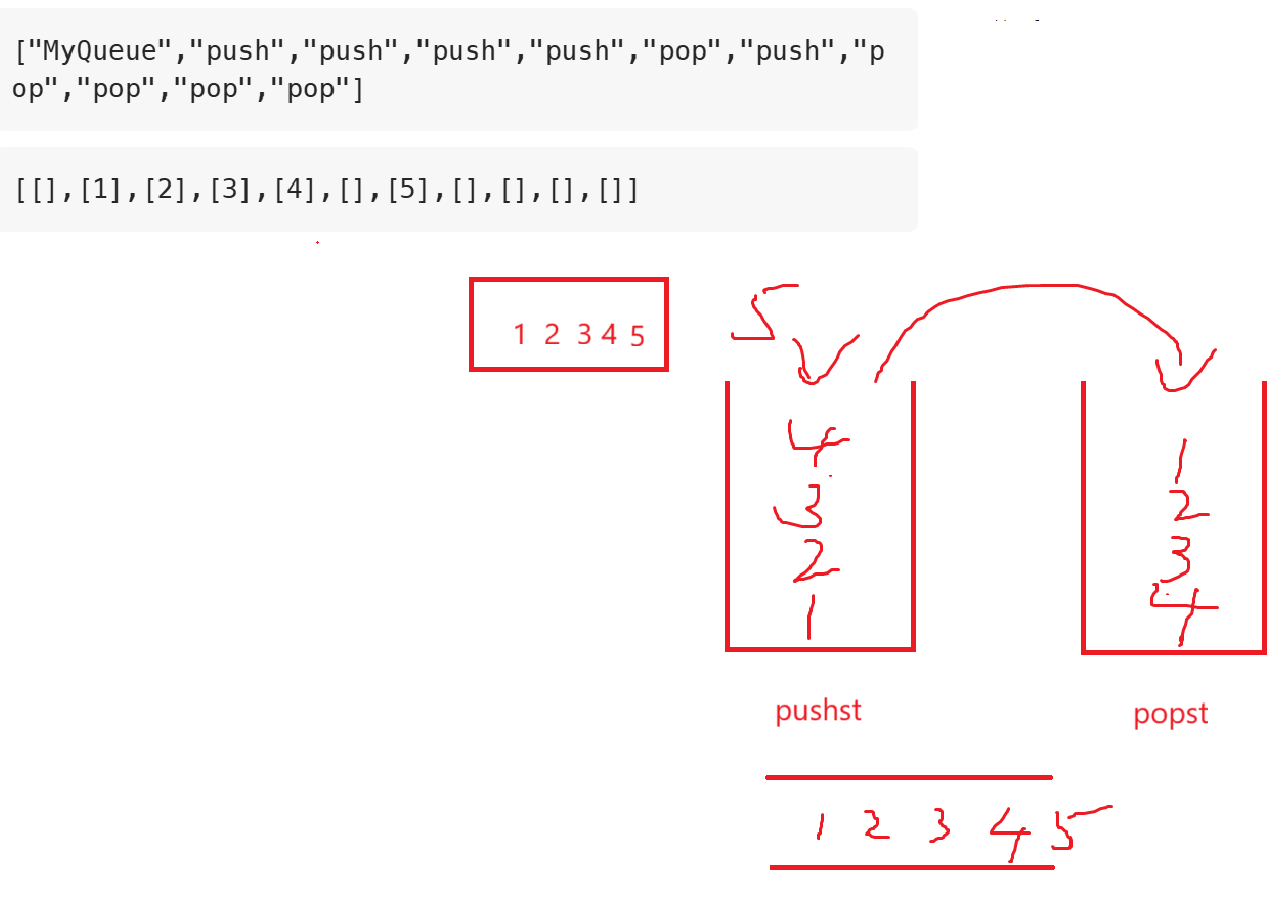
pop时优先pop和peek popst的值，真没值了再从pushst中拷贝。
四、逆波兰表达式求值
150. 逆波兰表达式求值 - 力扣（LeetCode）
大概搜了一下这个逆波兰表达式，主要作用就是因为计算机底层如果需要读优先级和括号，就降低运算的效率。
我们一般用的叫中缀表达式，而逆波兰表达式其实是后缀表达式，把运算符放到两个运算数后，读到运算符以后就把前面的两个运算数带入：
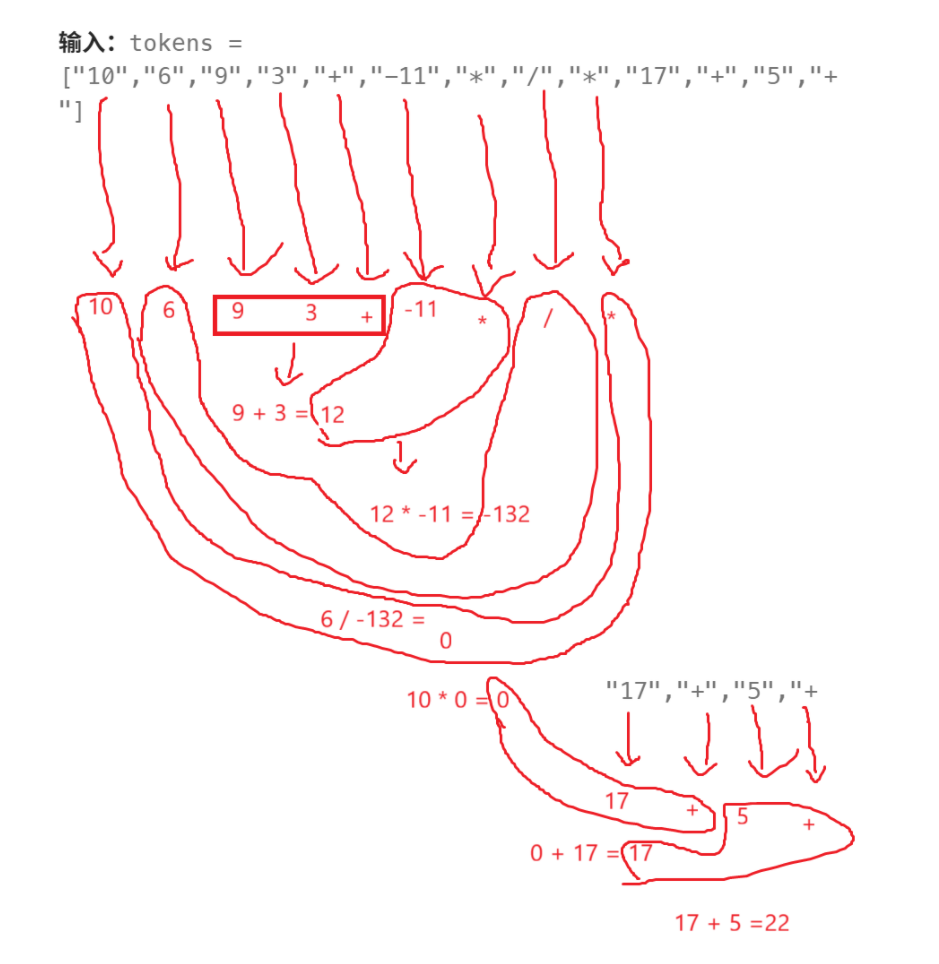
大概意思就是这样的，其实理解了后缀表达式之后很容易想到，直接用栈就行，如果读到运算符，那就弹出栈顶的两个数，如果读到数就入栈，也就是：
并且需要注意的是，第一个弹出来的是右操作数，第二个弹出来的是左操作数，+ *我不挑你的理，假如- /呢？
12 - -11和-11 - 12
6 / 3 和3 / 6
所以一定得顾好左操作数和有操作数的顺序。
另外读典例和输入我注意到，如果直接以string[0]=="+" "-" "*" "/"为判断条件，负数的符号将会被错误辨别，因此还得注意判断string的长度来判断这到底是一个负数的负号还是一个减号。
class Solution {
public:int evalRPN(vector<string>& tokens) {stack<int> st;for(auto& e: tokens){if((e[0] == '+'||e[0] == '-'||e[0] == '*'||e[0] == '/')&&e.size() == 1){int right = st.top();st.pop();int left = st.top();st.pop();switch (e[0]){case '+':st.push(left + right);break;case '-':st.push(left - right);break;case '*':st.push(left * right);break;case '/':st.push(left / right);break;default:break;}}elsest.push(stoi(e));}return st.top();}
};如果这道题要求先拆成后缀表达式然后再计算，那可就要了老命了，如果只计算，那就是充分利用stack的特性保证运算顺序即可。
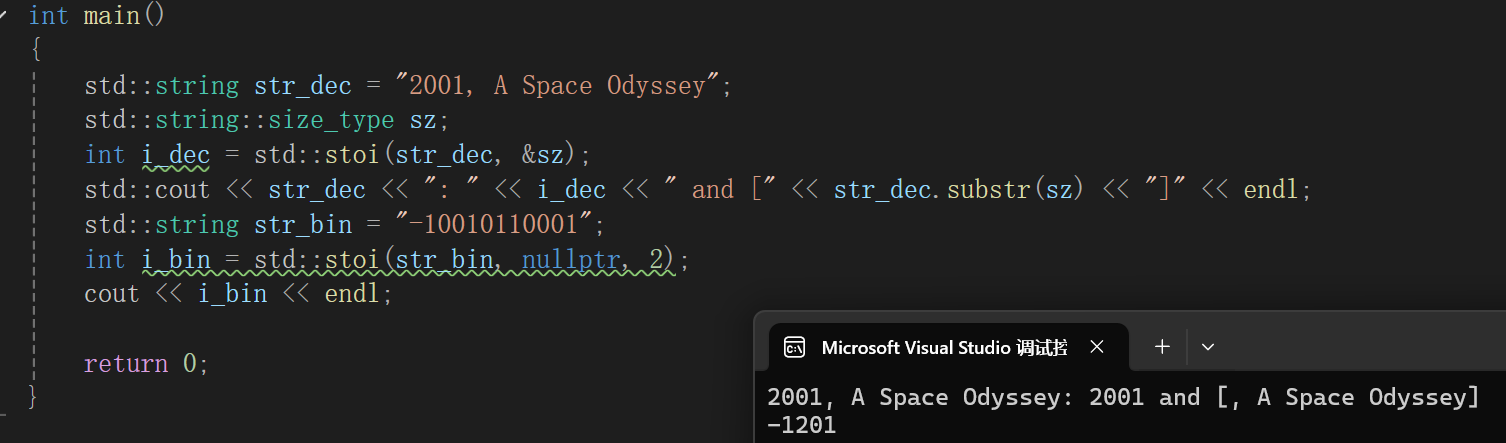
没啥可说的，唯一用了个stoi查了查库，其它的就是图咋画，代码咋写。
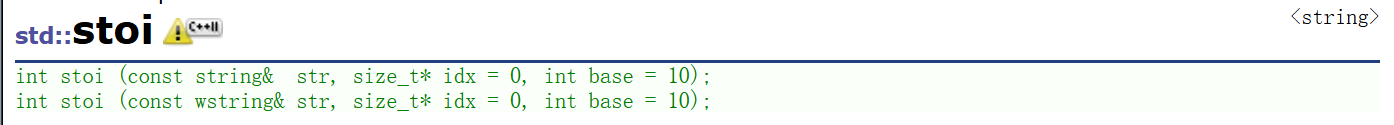第一个参数传需要转换的string对象，这个不用解释；
第二个参数idx是个指针变量，如果你想知道str在哪里开始不能再转换成数字的第一个字符的地址，那就传一个指针变量，这个函数就会把这个地址存到这个指针变量上；
最后一个参数是，str里的数字字符以多少进制的方式转换。
测试代码，直接扣的库里面的：
五、数组中的第K个最大元素
215. 数组中的第K个最大元素 - 力扣（LeetCode）
经典的top-k问题，用堆解决，或者换句话来说，用priority-queue来解决：
class Solution {
public:int findKthLargest(vector<int>& nums, int k) {priority_queue<int> pq(nums.begin(),nums.end());for(int i = 0;i < k - 1;i++)pq.pop();return pq.top();}
};只不过不要前k个，只要第k个。