当前位置：首页 > news >正文

算法（一）双指针法

news 2025/9/19 15:04:50

一、移动零

283. 移动零 - 力扣（LeetCode）

题目其实难度不高，重点是双指针这个方法。

看见这题下意识第一反应就是用两个指针，一个指针在前面找0，另一个指针在后面站岗随时准备交换。但是看见非零元素的相对顺序不变就只能换办法。

而后就能想到，如果碰见0元素，计数，并且利用类似于string/vector这些顺序表的erase方法的思路，可以

while(pcur != end)

{

nums[pcur - 1] = nums[pcur];

pcur++;
}

但是这样的话免不了循环套循环，移动次数也非常多。

所以这次我们类比快速排序的思路来做：

依旧是两个指针，根据指针来分区间。

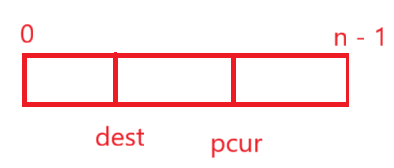
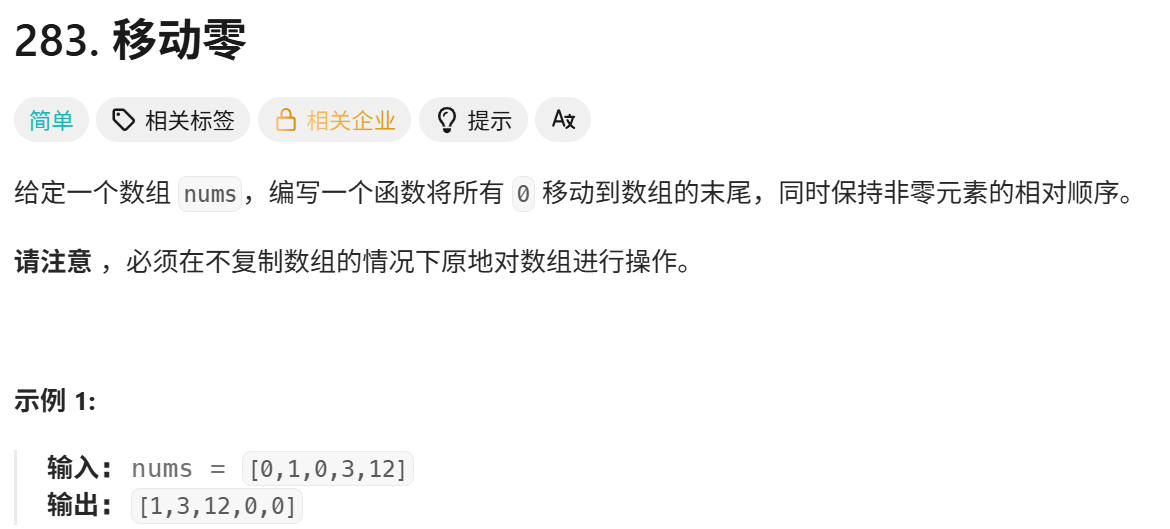
有效元素范围是[0,n-1]，其中[0,dest]代表已经处理过的非0的元素区间；[dest + 1,pcur - 1]表示已经处理过的全是0元素的区间；[pcur,n - 1]代表未处理的元素。

拿过来典例：

初始情况下就让dest出于下标-1的位置，pcur位于数组起始位置。循环条件很明显，就是pcur越界不越界即pcur < n。

pcur遍历到0

看着图走读，pcur如果碰见0那往后走还是做处理，往后直接走是：

此时dest左侧没有区间，[dest+1,pcur-1]为0，pcur后为未处理，其实是符合我们对区间的划分。

故而pcur碰见0就不管它，继续往后遍历。

pcur遍历到非0

下次遍历碰见的是非0元素，碰见非0元素那么dest左侧的区间就该扩张了，如果放着不管就相当于扩张全0区间[dest + 1,pcur - 1]，怎样才能完成扩张呢？

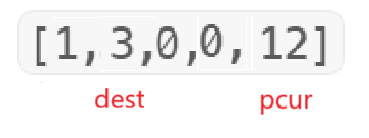
注意到此时dest后一个位置是0，而pcur位置为非0，并且pcur++后原位置应为0，故直接swap，需要注意的是swap(dest + 1,pcur)。

故而pcur碰见非0需要操控使得0与非0互换位置。

重复以上过程即可

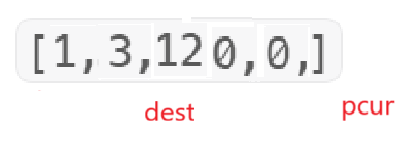
（本人暂时未去尝试那种动态的gif图怎么做，所以展现遍历只能通过一次一次截图了）

思路就是这样，代码表达：

class Solution {
public:void moveZeroes(vector<int>& nums) {int pcur = 0;int dest = -1;while(pcur < nums.size()){if(nums[pcur] == 0){++pcur;}else{++dest;swap(nums[dest],nums[pcur]);++pcur;}}}
};

当然，OJ题写成这样可不一定能通过，得考虑考虑有没有极端情况。

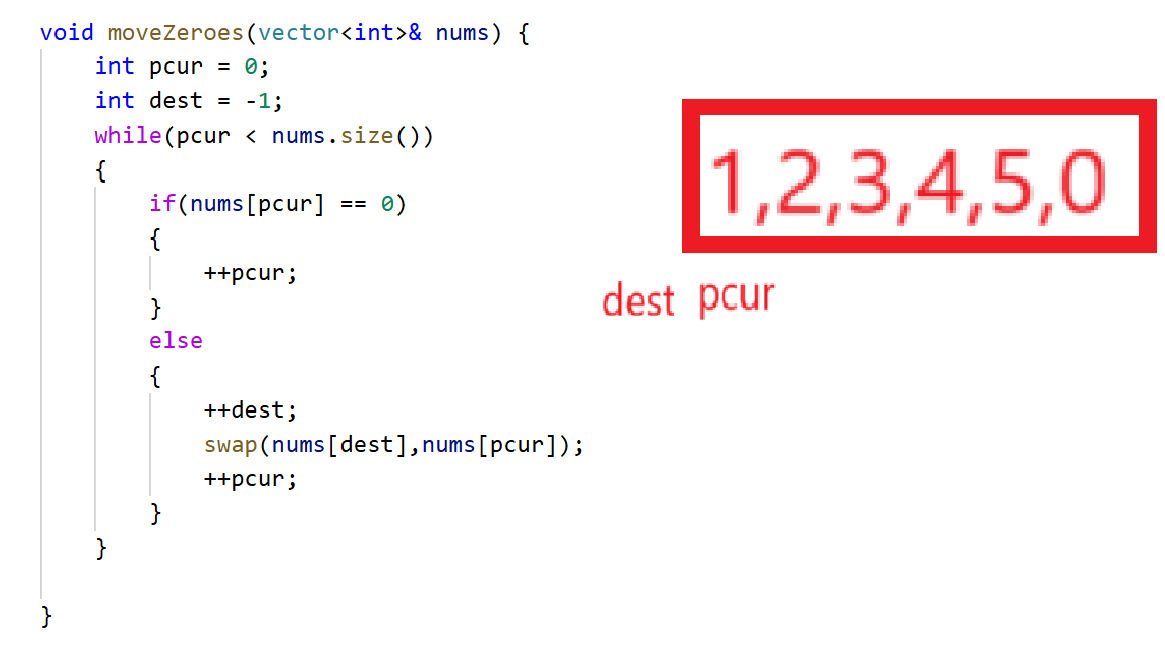
不难观察到，如果根本不需要移动0的情况下，++dest后dest == pcur，这个时候的swap毫无意义，其实可以if一下到时候跳过（不过倒也不影响结果正确性）。

再来个：

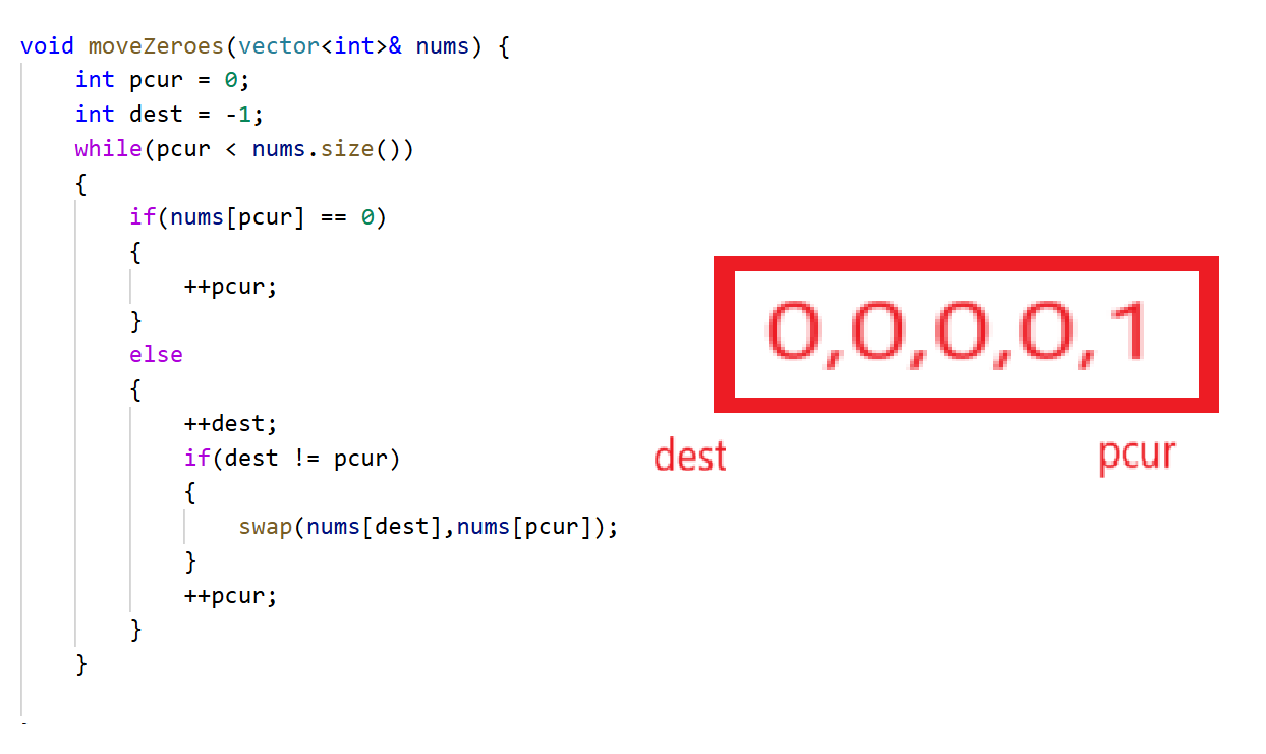
看着也没问题，因为是0的话pcur都不管，碰见非0交换也没啥毛病。

测试下呗：

暂时想不到啥麻烦事了，先提交吧：

过了，那没啥可说的了。

class Solution {
public:void moveZeroes(vector<int>& nums) {int pcur = 0;int dest = -1;while(pcur < nums.size()){if(nums[pcur] == 0){++pcur;}else{++dest;if(dest != pcur){swap(nums[dest],nums[pcur]);}++pcur;}}}
};

另外，做算法题开始我就不是特殊情况，我就逼自己用前置++了，因为最近学的容器，也模拟实现了不少，我发现实现起来前置++比后置++少个拷贝构造，所以逼自己习惯前置++吧（毕竟我其实老喜欢用后置++了）。

二、复写零

1089. 复写零 - 力扣（LeetCode）

光看这个描述其实有点抽象，结合着典例来看：

碰见零就复写，原来数组里零位置后面的元素通通后移，越界的就不管了。

1.最容易想到异地复写

很容易想到：

创建一个与原数组完全相同大小的数组，利用pcur指针遍历原数组，如果碰见非零元素就拷贝一次到临时数组里，如果遇见零那就拷贝两次，直至dest越界。

这个方法时间复杂度空间复杂度都很明显是O(n)，但是题目里早就知道你会这么干：

真是无奈啊，人家故意加粗，就是非得让你以O(1)原地实现。

2.原地从前往后复写尝试

没招了，只能是原地了：

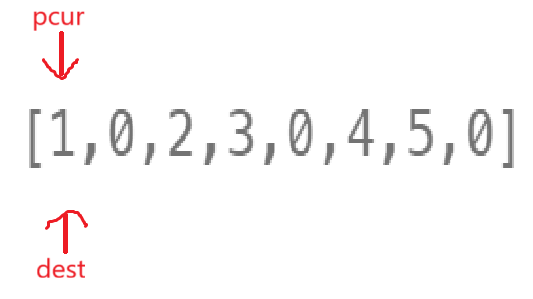
现在原地的思路就是由pcur检测当前是非零元素还是零，根据dest的指向做duplicate。

第一次pcur == 1，往dest位置赋1；二者操作完以后都++

第二次pcur == 0，所以就连续让dest赋值两次零：

完成操作后都++。

好了，已经结束了，真按照图上这么干，碰见一个0你就会发现剩下的后继元素啥都不管了，全成零了。

代码陷入停滞了，不让我异地，我原地失败了那我还干鸡毛，其实我碰见这种情况就是这么想的，但是说归说骂归骂，一地鸡毛生活还得继续过啊。

3.从前往后复写修改Ⅰ

肯定还是原地复写，而既然你现在出现的问题是零元素后紧跟着的元素，不管是零还是非零，均会被覆盖，那这样呗，干脆碰见零我就把零后的元素存起来，等到下次遍历的时候直接检测这个临时存起来的元素。

尝试尝试昂：

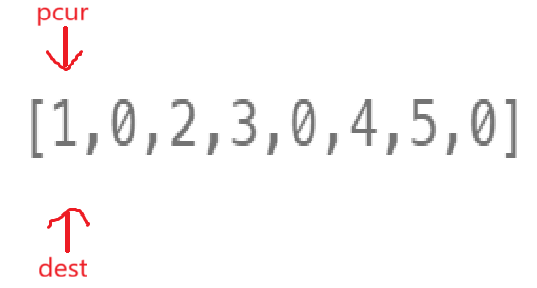
这么干第一次还是一看，没碰到0就没事，直接++。

进入第二次检测：

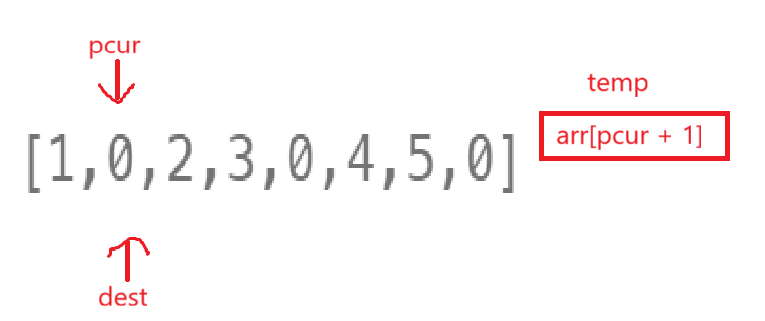
碰见零就得开始存值了。

捋下思路昂：

①碰见0就得存值，所以就存arr[pcur+1]；之后++dest，++pcur

②存值以后没有后顾之忧了，所以就dest连续复写两次0；之后++dest

这次完了以后很明显pcur已经失去遍历的效果了，下次遍历的是temp == 2：

③temp不为0，swap(arr[dest],temp)；dest++

这次遍历需要检查的就是原数组理论上的下一个元素也就是temp，不过可不能傻的直接说，检测到temp != 0所以就直接往dest位置插入，这样3（下次应该遍历的数据）就会被覆盖，最好的做法就是swap(arr[dest],temp)，这样不仅做到了覆盖，也做到了保留下次遍历到的值。

temp仍不为0，那就继续swap并++。

④temp为0，记录下此次dest位置的值（理论上下次需要遍历到的值），并且连续复写两次0。之后++dest

但是这个时候我们注意到4后的5被覆盖掉了，如果arr再长一点，就又无法交代了。

解决的办法倒是也有，等于碰见几个0我就得记录0后多少个数呗，麻烦点一个是又得定义一个变量专门记录遍历到的0的个数，除此之外最麻烦的就是怎么记录这么多个值。

后来我一细想，其实可以搞个vector，申请固定大小的int，初始全部都弄成-1，充分利用：

如果vector全部为-1，那说明没有碰到0，一直后移指针就行了，如果前m个值均为有效元素（包括0），那就先遍历完整个vector，不过一细想，这种情况用队列不更好，但是这么弄不跟原来异地复写差不多嘛。

4.从前往后复写修改Ⅱ

刚才我是从每次遍历入手，强制存起来可能被覆盖的值，但是最极端的情况，全部是0，那么没碰见一个0，按照我上面的思路，碰见第一个0存储后面一个元素，接下来碰见第二个0存储后面两个元素，第三个存储后面三个，直至把当前遍历的元素的后面所有元素存起来，这么弄起来空间复杂度将近O(n)不说，代码麻烦程度上升老多了，等于就为了个原地算法，逼的自己写成四不像了。

不过没事，我们原地算法还有修改的方向，既然从前往后复写会覆盖，那我从前往后如何呢。

简单来说就是站在答案的角度，我们知道最后一个被复制的元素是谁的话，dest从后往前写绝对不会覆盖有效元素了，最多覆盖无效元素，无效元素咱们管它干嘛呢？

这样的话碰见非零复写一次，碰见零复写两次。

大概就是：

①pcur != 0,arr[dest] = arr[pcur];--pcur,--dest

②pcur == 0,arr[dest] = arr[pcur],--dest,arr[dest] = arr[pcur];--pcur,--dest

至于结束条件，从结果出发肯定最后pcur和dest同时到达下标为0的地方了，所以随便写个pcur > 0/pcur >= 0/dest > 0/dest >= 0。

所以难点不是实现从后往前遍历复写，难点转变为，我怎么知道最后一个复写的是谁呢？

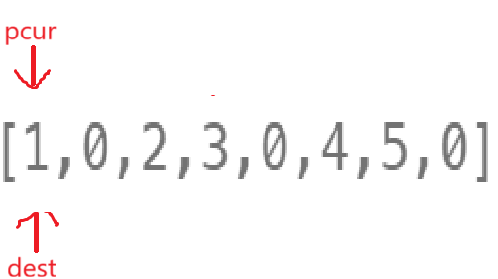
这事还真能办，毕竟重点是什么重点是我们要找到最后一个被复写的元素，那干脆空遍历呗，也就是真根据pcur指向的数据移动dest指针，不真的去赋值就行了。

那这就简单了：

①pcur != 0,++pcur,++dest

②pcur == 0,++dest;++pcur,++dest也就是dest += 2,++pcur

终于有个既好写有容易理解的法子了，这题都给我算成简单，我画画图，试着写写代码，再写写文章，一道题用了三四个小时。

class Solution {
public:void duplicateZeros(vector<int>& arr) {int pcur = 0;int dest = 0;//调整dest和pcur为最后一次复写指向while (dest < arr.size()){if (arr[pcur] != 0)++dest;elsedest += 2;if(dest < arr.size())++pcur;}//从后往前修改while (pcur >= 0){if (arr[pcur] != 0)arr[dest--] = arr[pcur];else{arr[dest--] = 0;arr[dest--] = 0;}--pcur;}}
};

说我堆栈出问题了，没办法了只能打开VS调试看看了。

走读代码

走读代码容易发现，循环走完是这样的，正常走完循环其实pcur和dest都多走了，并且想到：

最后一个是0的话，pcur多走一步就不说了，dest多走两步，所以干脆：

class Solution {
public:void duplicateZeros(vector<int>& arr) {int pcur = 0;int dest = 0;//调整dest和pcur为最后一次复写指向while (dest < arr.size()){if (arr[pcur] != 0)++dest;elsedest += 2;if(dest < arr.size())++pcur;}if (dest == arr.size())--dest;else if (dest > arr.size()){dest = arr.size() - 1;arr[dest--] = 0;--pcur;}//从后往前修改while (pcur >= 0){if (arr[pcur] != 0)arr[dest--] = arr[pcur];else{arr[dest--] = 0;arr[dest--] = 0;}--pcur;}}
};

一测试：

总算是通过了。

三、快乐数

202. 快乐数 - 力扣（LeetCode）

依旧抽象，所以还是看看典例：

那这就知道了，每次把每一位取出来再平方相加，如果是快乐数，最后就变为1而且可知，变成1以后就无限循环了。

但是还有一种情况：

这个数为什么不是快乐数呢？

2->4->16->37->58->89->161->38->73->58

无限循环了成。

等于输入的数字会出现两种情况：

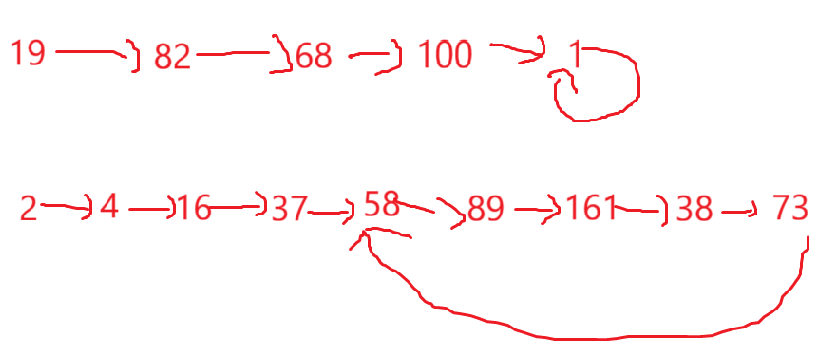
这玩意看着好熟悉啊，如果还想不起来：

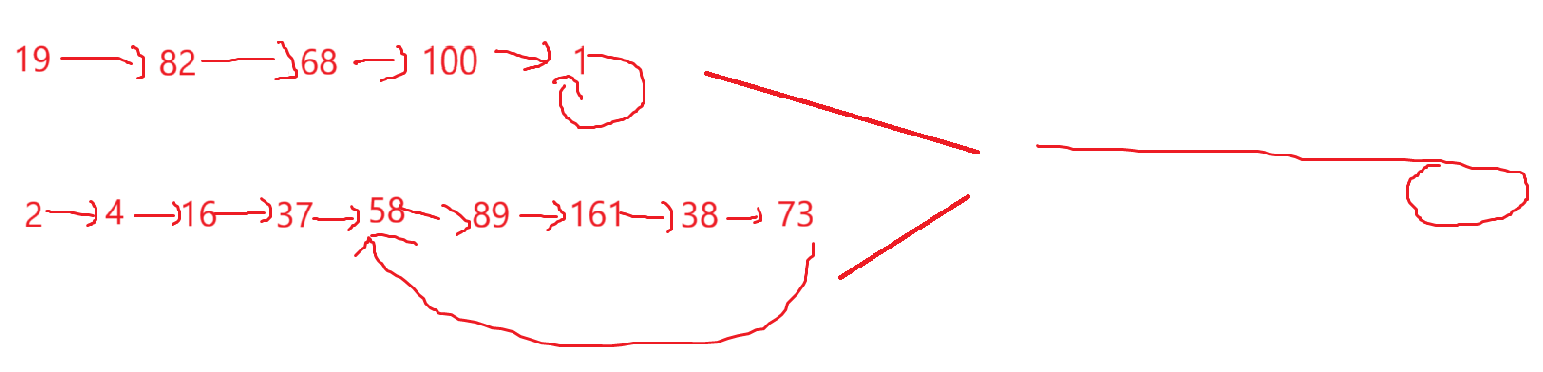
带环的链表。

为什么又提到了带环链表呢？

如果将快乐数生成的序列看成链表的话，那么快乐数生成的链表是以1为环的链表；

如果将非快乐数生成的序列看成链表的话，那么非快乐数生成的链表也是有环的，但是这个环不存在元素为1的结点。

一看见带环的链表，我们就不禁想快慢指针，因为至少有两道，链表是否有环、带环链表的环入口结点位置，那么这道题也可以用快慢指针来做吗？

答案是肯定的，我们可以利用快慢指针必然在环中相遇的特点，即如果相遇时指向元素值为1那就是快乐数，反之不是。

唯一麻烦的就是怎么用快乐数序列实现链表的快慢指针用法，其实很简单：

class Solution {
public:int sqsum(int num){int sum = 0;while(num){sum += (num % 10)*(num % 10);num /= 10;}return sum;}bool isHappy(int n) {int fast = sqsum(sqsum(n));int slow = sqsum(n);while(fast != slow){fast = sqsum(sqsum(fast));slow = sqsum(slow);}if(fast == 1)return true;elsereturn false;}
};

随便写了个函数把一个数每位的平方和表达了一下，而fast初始化用求两次平方和，slow用一次，相当于直接开始：

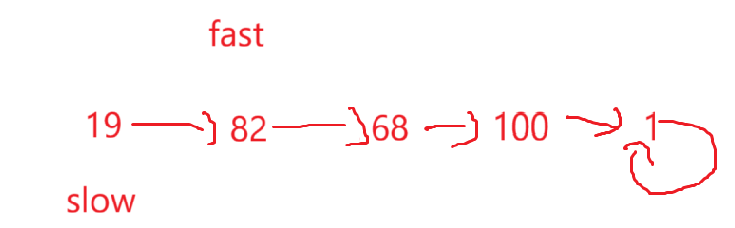
之后每次往后走fast相当于走两步，slow相当于走一步。

我们学过链表，并且学过带环链表的判断条件以后其实这题也就那样，问题就在于，我其实对这个有点不理解：

如果一个数不是快乐数的话，难道就必须无限循环下去吗？

不过这个我搜了搜，其实还挺好理解的：

int大概是 $2^{31} - 1$ 大概看看昂：

二十多亿一个数字吧，一共十位，就说成9999999999，这个数如果算平方和很容易算出来810，那么这样这肯定能包含所有整型值得平方和了吧，所有整型的平方和取值不到810个数，如果一个数不无限循环，假设就让它连续算810次，你就硬说它把不到810个情况全部取完（因为假设不循环嘛），那第811次是不是一定就能取到了。因为取值就那么多，你一直算下去怎么可能一个都取不到，所以肯定是会有循环的。

也就是说一个数要不然每位平方和一定会产生一系列数的循环。

四、盛水最多的容器

11. 盛最多水的容器 - 力扣（LeetCode）

解法1

那还说啥了兄弟，你让我算盛水最多的容器，我就把你能组成的所有容器都算了，然后筛选出来体积最大的就行了。

代码基本逻辑其实也没多难，但是弄个 $n^{2}$ 人家都不给你过，专门弄个老大的测试样例，那没办法，换办法呗，不然还能咋。

解法2

这方法纯粹借鉴，因为我真没招了，不过硬说其实是利用数学性质借助双指针实现，本质上还是枚举，但是不是一个一个枚举，而是一个一个选择性的枚举。

数学性质是这样的：

这是用双指针随意圈定的区间，还是要一个一个枚举：

但是有这样一个性质：

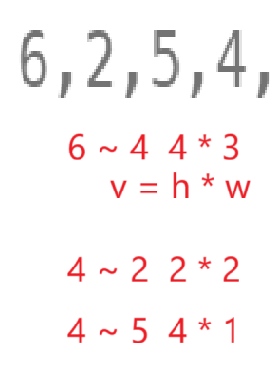
观察到区间端点可以算出来一个体积，如果让高度较小的值向内枚举，举例说明：

首先明确，向内找，容器的宽度一定会减少，这是一定的事。

4 ~ 2 -> 2 * 2，宽度减少，且由于找的高度比较小值小，所以高度也减少，总的说来相对于区间端点所得体积是小的；

4 ~ 5 -> 4 * 1，宽度减少，由于找的高度比最小值大，根据短板效应，木桶存水最大高度取决于较小值则高度不变。高度不变宽度减小，总的来说相对于区间端点所得体积是小的。

也就是说，区间端点较小值没必要再向内枚举，得到的值绝对没区间端点所得体积大。

利用这样的性质，只用区间端点较大值向内枚举，大大较少枚举的次数，而且，由于我们是通过指针控制容器端点来遍历，当两端指针交汇就停止，可想而知时间复杂度也就O(n)。

代码表达：

class Solution {
public:int maxArea(vector<int>& height) {vector<int> v;int left = 0;int right = height.size() - 1;while(left < right){v.push_back((right - left) * (height[left] < height[right]?height[left]:height[right]));if(height[left] <= height[right])++left;else--right;}int max = 0;for(auto& e: v){max = max >= e ? max : e;}return max;}
};

重点还是这个性质,有了性质代码不难写。

当然写完以后突然感觉写的冗杂，首先是发现库里其实有max和min函数，就是用来求最大最小值的，再来就是其实创建个返回值就行，这个容器不太有必要：

class Solution {
public:int maxArea(vector<int>& height) {int ret = 0;int left = 0;int right = height.size() - 1;while(left < right){int v = (right - left) * min(height[left],height[right]);ret = max(ret,v);if(height[left] <= height[right])++left;else--right;}return ret;}
};

叫我说，我这真跟小孩一样，我想了想我自己都笑了，因为已经学了几个容器了嘛，干啥事都想装装我多会用容器，招笑。

五、有效三角形的个数

611. 有效三角形的个数 - 力扣（LeetCode）

描述依旧抽象，拿出来典例结合着看：

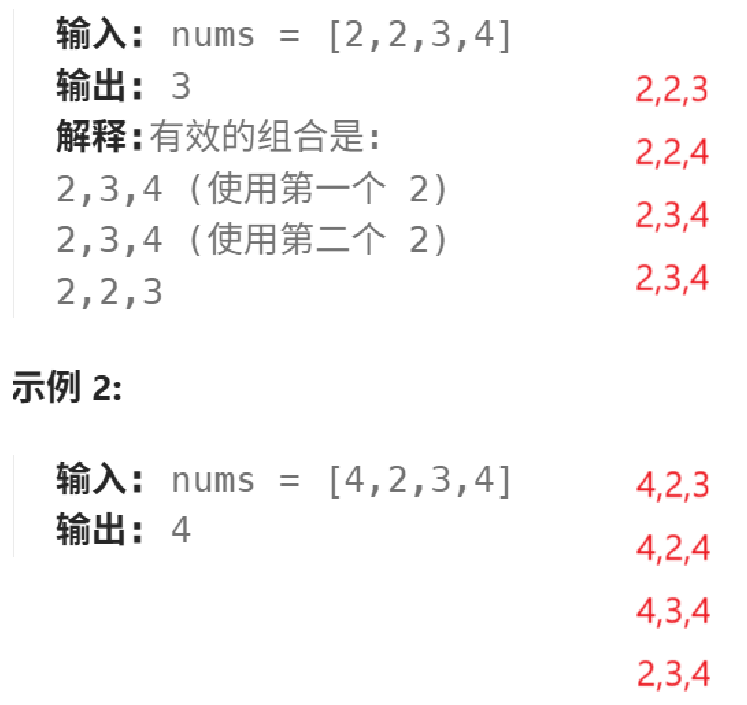
题意就是提供一个数组，数组中每个数都代表着三角形边长，任意选三条边组成三角形，要求最后输出这个数组能组成的所有三角形个数。

大概用到的判断就是三角形的两边和大于第三边。

暴力枚举

暴力解法很容易想到：

for(size_t i = 0;i<nums.size();i++)
for(size_t j = i + 1;j < nums.size();j++)

for(size_t k = j + 1；k < nums.size();k++)

check(nums[i],nums[j],nums[j]);

多好说，直接暴力枚举出所有的三元组，每个都筛选，正确就计数+1，不正确就检查下一个。

随便写了写思路就发现实际上这个事不太走的通，时间复杂度太大了，到时候不炸才怪，估计也就短数组的判断还能算得上。

减少枚举次数的优化

我们上一题算盛水最多的容器的时候刚开始也是暴力枚举，后来经过了对条件的细致的分析从而减少了枚举的次数，注意，是减少了枚举的次数，不必枚举的就直接跳过，但是实质上还是枚举，但是重点是让计算机模拟人的筛选。

其实如果abc的大小是这样的情况的话，注意到，如果a + b > c成立，那么很容易能够得到其它两个条件必然成立，因为c是最大值，只有这里可能会出现差错。

所以判断是否是三角形就从三个判断条件变为两个较小值大于最大值，想要做到a <= b <= c，最简单的办法就是排序，排好序再从左中右各选一条边必然可以符合条件。

比如有排好序的这样一个序列：

固定large在large左侧的区间枚举，也就是在large左侧区间找符合条件的二元组：

①nums[left] + nums[right] <= nums[large]

此时1和最大的数都不能组成三角形，则1和其它任意元素组成的二元组都不符合条件，所以++left舍去1做三角形边长的枚举：

②nums[left] + nums[right] > nums[large]

此时发现left和right相加大于large，那么现在left位置往后的所有位置都可以与现在的right组成三角形，也就是8和区间剩下元素组成的二元组一定可以组成三角形，因为++left的过程两边之和一直在增加。一共是right - left种情况。

结算完以后，right指向8的所有情况统计完了，8就不用枚举了，用过了，枚举失效了嘛，此时还剩--right后的区间没有检查。

最后写成代码：

class Solution {
public:int triangleNumber(vector<int>& nums) {int ret = 0;sort(nums.begin(),nums.end());for(size_t i = nums.size() - 1;i >= 2;i--){int left = 0;int right = i - 1;while(left < right){if(nums[left] + nums[right] > nums[i]){ret += right - left;--right;}else++left;}}return ret;}
};

六、查找总价格为目标值的两个商品

LCR 179. 查找总价格为目标值的两个商品 - 力扣（LeetCode）

一看典例：

大概思路就出来了，双指针，充分利用单调性，类似于盛水最多的容器和三角形个数一样的遍历方法。

当然，即使我们知道能用双指针解决还是得思考一下暴力枚举：

for(size_t i = 0;i < price.size();i++)

for(size_t j = i + 1;j < price.size();j++)

check(price[i],price[j];

大致思路就是全部枚举，for套for，处理正确以后再处理就行。

时间复杂度也不用多说了，就是O( $n^{2}$ )。

暴力枚举就是没有利用单调性，我们可以这样：

初始状况是这样的，肉眼一眼就看出来left+right的值要大于target，因为单调性，可以知道此时的left前所有与66相加的数都将大于target，66的所有枚举就没有意义了，所以此时--righ把66的所有枚举略去，即：
left + right > target -> --right

这样就省去了很多次枚举。

继续检查，left + right < target了吧，那么这个时候固定8，right左侧所有值与8相加都将小于target，所以在这个区间8的所有枚举都将失去意义，所以此时--left把8的所有枚举略去，即：

left + right < target -> ++left

继续检查，可知lleft + right > target -> --right

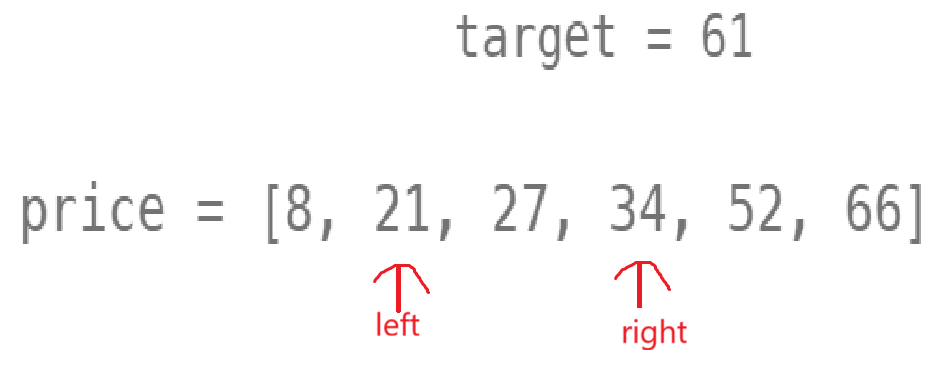
left + right < target -> ++left

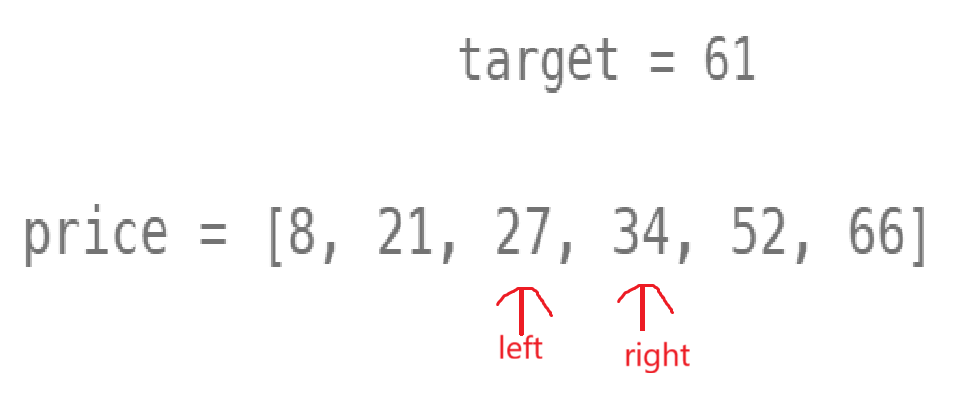
相等直接返回left和right指向的值。

class Solution {
public:vector<int> twoSum(vector<int>& price, int target) {vector<int> v;int left = 0;int right = price.size() - 1;while(left < right){if(price[left] + price[right] > target)--right;else if(price[left] + price[right] < target)++left;else{v.push_back(price[left]);v.push_back(price[right]);return v;}}return v;}
};

咋说呢这题，思路咱也接触过，倒是不难，额外再说就是因为，实际上题意就是说一定能找到两个price的和为target，最外层的return v其实没啥用，因为它也没说如果没有符合的返回什么，但按题意根本到不了这层。

七、三数之和

15. 三数之和 - 力扣（LeetCode）

两数之和做过以后，我们不禁想，能不能用同样的方法解决问题，只不过这次有点特殊，用双指针肯定还是有单调性好一点，这样的话方便用双指针来确定区间。

思路是这样的，为了能够用上双指针，我们首先sort使得整个数组有序，有序以后一个数一个数的遍历，将此次遍历到的数当作三元组的其中一个元素，三元组的要求是最后三个数之和为0，那么容易知道，其它两个元素符合要求的条件就是两元素之和刚好是此次遍历到的元素的相反数。

区间内双指针这么用：

left + right < -i

则说明left + right的值小了，那么此时移动谁呢？
假设移动right，因为此时数组有序，right左移是向小数移，那么一定不能找到目标情况，所以左移right是错误选择；

假如移动lleft，因为此时数组有序，left右移是向大数移，那么有可能找到目标情况，所以应该右移left并检查。

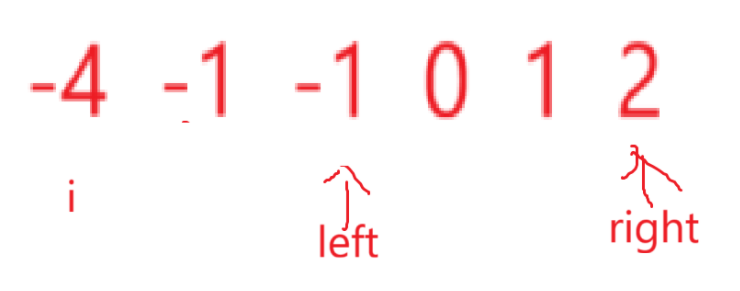
同理

经典的双指针相遇循环结束。此次遍历证明-4绝对不是结果三元组里的元素。

改变i重置left和right：

此时left + right == -i，那么我们做的处理应该是将此时三个指针指向的元素作为一个有效三元组返回。

注意，绝对不能说碰见了一个答案就停止，很明显肉眼观察-1 0 1也是符合要求的，所以如果碰到答案，正确的做法是++left和--right，继续检查，因为同时移动left和right有可能形成和不变的情况。

同样返回有效三元组。

再遍历就相遇并错过，此时进入下次循环：

注意题意：

这个时候就能体现出来排序的第二个好处，相同的值都在一起，这样的话可以写条件：

i ? i - 1

i == i - 1->continue，当然写这个条件肯定得i > 0，不然又越界了，而且按道理来说第一个元素去哪跟前面重复。

另外在双指针区间内：

在这样的条件下会出现：

所以在双指针区间内的left和right同样得检查left - 1和right + 1。

再来就是想起来个：

这个被记录，继续循环：

很容易干越界，但是好像不影响，如果根据for的条件来看的话，好像也没事：

class Solution {
public:vector<vector<int>> threeSum(vector<int>& nums) {sort(nums.begin(), nums.end());vector<vector<int>> vv;for (size_t i = 0; i <= nums.size() - 3; i++){if (i > 0 && nums[i] == nums[i - 1])continue;int left = i + 1;int right = nums.size() - 1;while (left < right){if (nums[left] + nums[right] < -nums[i])++left;else if (nums[left] + nums[right] > -nums[i])--right;else{if (left - 1 != i && nums[left] == nums[left - 1])++left;else if (right != nums.size() - 1 && nums[right] == nums[right + 1])--right;else{vv.push_back({ nums[i],nums[left],nums[right] });++left;--right;}}}}return vv;}
};

其中i <=是看的：

数数就知道是size - 3了。

另外，else内层的if和else if，left是防止left - 1 == i而导致的情况缺少：

此时如果不管left - 1 != i，那么这种情况将会被：

right是怕right + 1越界访问。

八、四数之和

18. 四数之和 - 力扣（LeetCode）

那还说啥了兄弟，你是真能整我啊，三数之和完了给我干个四数之和，一层一层的套，我要是暴力那不炸了，直接O( $n^{4}$ )，自己选的题自己宠吧，那还能咋。

依旧想办法扣出来双指针，为了搞成双指针，大概率我得固定俩数，不过还是先排序：

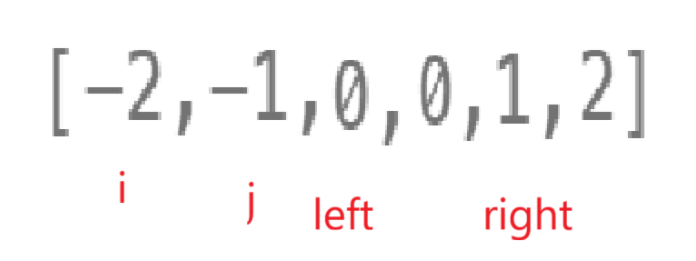
一观察，看来最后i得遍历到size() - 4，j得遍历到size() - 3，left和right依旧一个j + 1一个size() - 1，这哥俩相互制约left < right，老生常谈了真不多说啥了。

其它思路就类比三数之和，固定i，则j + left + right = target - i，固定j则left + right = target - i - j。

写三数之和有俩重点：
1.不漏

不能说找到left + right = target - i - j任务都结束了，同时移动left和right还是有可能符合条件的
继续同时--left和++right。

2.不重

从内向外走：
left - 1!= j&&left == left - 1->++left

right + 1<size()&&right == right - 1->--right

j肯定还不能跟之前的相等

j - 1 != i && j - 1 == j->++j

i同理，只不过它是不能越界

i - 1 != 0&& i - 1 ==i->++i

当然，根据我们三数之和的经验，i和j的操纵就以continue来。

可能说对上面我框框写出来的条件有疑问，其实我也不是说瞎猜的：

left可以等与j吧，但是这个时候left - 1 == j，你要是只写left == left - 1才++那扯不扯，有效情况也给你舍去了。

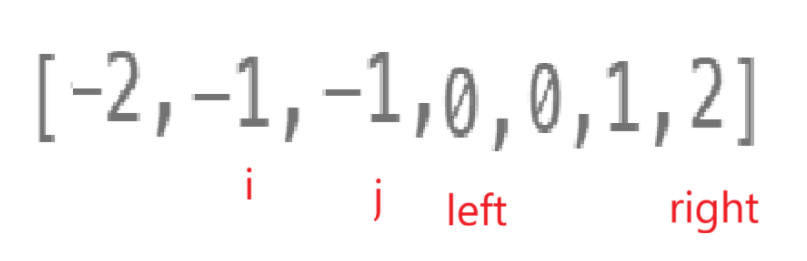
这个是j == i，但是j - 1 == i的条件，如果不写j - 1!= i那有效情况不没了。

至于i和right，它俩老在边界跳舞，防着点肯定是好的。

最后就是可能有人会想玩意i == i - 1不用去重呢？

重点就是我们先sort，相同的值肯定在一起：

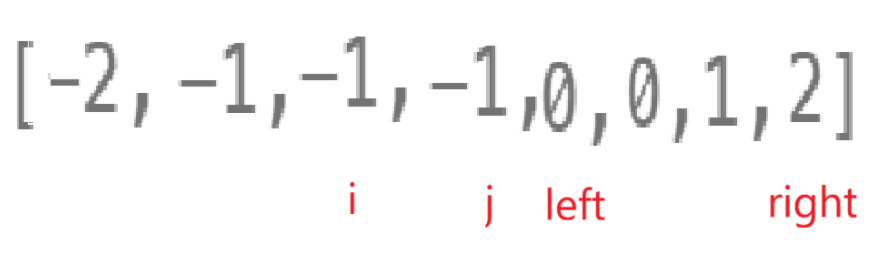
i++影不影响j和left right的值，看着确实不影响，但你移到最后一个相同的地方：

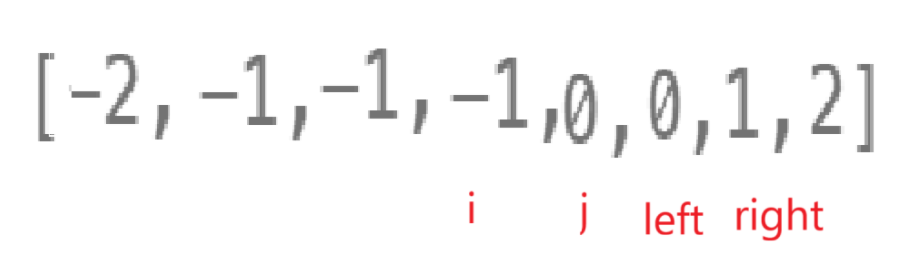
这个时候再i++就不礼貌了吧，所以除了上面说的，我还得再加一条，i - 1 == i&&i + 1 == i。

结果刚提交就炸了，太cs了：

而且它还没说如果没有结果返回啥，逆天。

第二次又炸了：

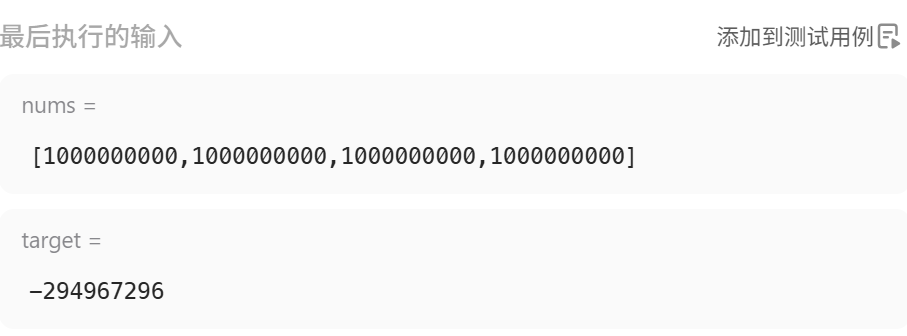
溢出了，我得发，真阴间啊。

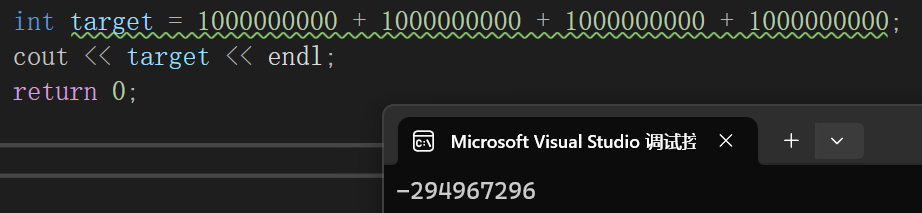
大概知道溢出就行了，所以最后代码：


class Solution {
public:vector<vector<int>> fourSum(vector<int>& nums, int target) {vector<vector<int>> v;if (nums.size() < 4)return v;sort(nums.begin(), nums.end());for (size_t i = 0; i <= nums.size() - 4; i++){if (i > 0 && nums[i] == nums[i - 1])continue;for (size_t j = i + 1; j <= nums.size() - 3; j++){if (j - 1 != i && nums[j] == nums[j - 1])continue;int left = j + 1;int right = nums.size() - 1;while (left < right){long long sum = (long long)nums[left] + nums[right] + nums[i] + nums[j];if (sum < target)++left;else if (sum > target)--right;else{if (left - 1 != j && nums[left] == nums[left - 1])++left;else if (right + 1 != nums.size() && nums[right] == nums[right + 1])--right;else{v.push_back({ nums[i],nums[j],nums[left],nums[right] });++left;--right;}}}}}return v;}
};

太阴间了，其实需求完成知道单调性下双指针，主要暗箭难防啊。