当前位置：首页 > news >正文

DeepSort学习与实践-原理学习

news 2025/9/19 9:15:06

DeepSort简介

DeepSort 是一种常用的多目标跟踪算法，基于 SORT 算法进行扩展。它通过融合目标的运动与深度外观特征，实现对检测到的多目标在视频中的持续身份跟踪。DeepSort 的作用是在每一帧图像中，将检测框关联到先前的轨迹上，从而为同一物体分配稳定的ID，实现连贯的轨迹。相比基础 SORT，DeepSort 利用 ReID 特征度量提高了匹配的准确率，能更好地区分外观相似的不同目标。DeepSort总体流程如下图：

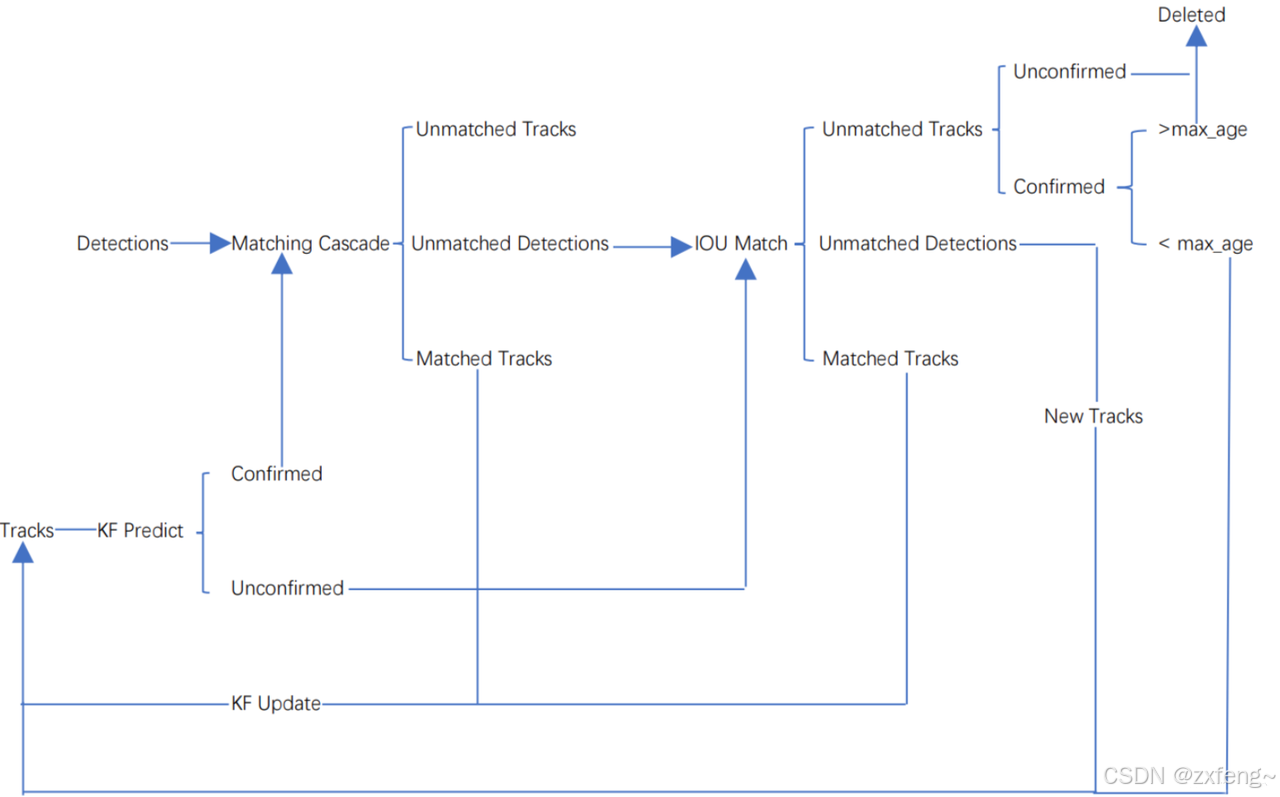
上图展示了 DeepSort 算法的跟踪流程图。可以看出，整个流程依次包括：对当前所有现有轨迹进行卡尔曼预测（KF Predict）、采用级联匹配策略将确认的轨迹与新检测框进行关联（Matching Cascade）、对未确认的轨迹和剩余的检测框进行 IOU 匹配（IOU Match），以及轨迹状态的更新（包括更新已有轨迹、初始化新轨迹和删除未命中轨迹）。

关键技术分析

卡尔曼滤波

卡尔曼滤波是一种针对线性高斯系统的最优递推估计算法，广泛应用于运动跟踪、信号处理、导航等领域。其核心思想是：利用系统的动力学模型对状态进行预测，并结合实际观测数据进行修正，实现对目标状态的最优估计。在卡尔曼滤波中，首先要对系统进行建模。其状态空间模型分为两个部分：状态转移方程和观测方程。状态转移方程描述系统在时间上的演化关系，具体表达为：
$x_k = A x_{k-1} + B u_k + w_k$
其中， $x_k$ 表示第 $k$ 步的系统状态， $A$ 为状态转移矩阵， $B$ 为控制输入矩阵， $u_k$ 为控制输入， $w_k$ 为过程噪声（均值为0，协方差为 $Q$ ）。
观测方程则描述了状态到观测的线性映射：
$y_k = C x_k + v_k$
其中， $y_k$ 为第 $k$ 步的观测值， $C$ 为观测矩阵， $v_k$ 为观测噪声（均值为0，协方差为 $R$ ）。
卡尔曼滤波的递推过程分为两个阶段：预测（Prediction）和更新（Update）。

预测阶段

预测阶段包括两个步骤：

状态预测：
$x^k∣k−1=Ax^k−1∣k−1+Buk\hat{x}_{k|k-1} = A \hat{x}_{k-1|k-1} + B u_k$
这一步利用上一步的最优估计和系统模型，预测当前时刻的状态。
协方差预测：
$P_{k|k-1} = A P_{k-1|k-1} A^T + Q$
这一步则是预测当前时刻的估计误差的协方差，其中的Q是噪声矩阵。

更新阶段

更新阶段包括三个步骤：

计算卡尔曼增益：
$K_k = P_{k|k-1} C^T (C P_{k|k-1} C^T + R)^{-1}$
卡尔曼增益 $K_k$ 决定了系统对预测和观测的权重分配，其中R是观测噪声协方差矩阵。
状态更新：
$x^k∣k=x^k∣k−1+Kk(yk−Cx^k∣k−1)\hat{x}_{k|k} = \hat{x}_{k|k-1} + K_k (y_k - C \hat{x}_{k|k-1})$
利用观测值对预测状态进行加权修正，获得本步的最优状态估计。
协方差更新：
$P_{k|k} = (I - K_k C) P_{k|k-1}$
更新最优估计的误差协方差。
其中， $x^k∣k−1\hat{x}_{k|k-1}$ 表示对第 $k$ 步状态的预测， $P_{k|k-1}$ 为预测协方差， $x^k∣k\hat{x}_{k|k}$ 为更新后的最优估计， $P_{k|k}$ 为最优估计协方差， $I$ 为单位矩阵。

卡尔曼滤波器通过这样的“预测—观测—更新”递推过程，在每一时刻不断融合模型先验和观测数据，实现对系统状态的最优估计。这种递归结构使其在实时动态系统中具有高效、鲁棒的特性。

在DeepSORT等多目标跟踪算法中，状态向量通常建模为多维（包含中心坐标、长宽、速度等），以描述目标的空间及尺度动态。卡尔曼滤波能够利用有限且带噪的观测，对目标的运动状态和尺度变化进行平滑估计，并在目标短暂消失（如遮挡、漏检）时，依然能凭借运动模型进行轨迹预测与补全，显著提升跟踪连续性与鲁棒性。

匈牙利算法

多目标跟踪问题的核心挑战在于：如何将检测结果和历史轨迹进行一一对应的全局最优匹配，以防止目标丢失和ID切换。DeepSORT采用匈牙利算法解决此检测框和轨迹的匹配任务。匈牙利算法是一种多项式时间复杂度的二分图匹配方法，用于寻找代价矩阵C的最小总权重分配。代价矩阵的每一元素定义为卡尔曼滤波预测框与检测框间的马氏距离或加入ReID特征后的加权距离：
$Ci,j=λ1dmotion(i,j)+λ2dappearance(i,j)C_{i,j}=\lambda_1 d_{motion}\left(i,j\right) + \lambda_2 d_{appearance}\left(i,j\right)$
其中， $d_{motion}$ 为马氏距离， $d_{appearance}$ 可为ReID特征的余弦或欧氏距离。

ReID

传统基于运动/几何信息的关联在面对目标密集、遮挡、交互等情景时易发生ID切换。为提升身份一致性，DeepSORT引入了基于深度学习的ReID（Re-Identification）模块，融合外观特征参与匹配。
ReID模块利用卷积神经网络（如ResNet、MobileNet等）对检测框裁剪区域提取高维向量（如128维），作为“目标外观指纹”。每个轨迹会维护历史外观特征库（如最近100帧，并选取目标与该若干帧之间的最小的距离作为该目标与当前轨迹的距离），系统在关联时将ReID距离纳入代价矩阵的计算，从而有效防止目标ID在空间位置模糊、遮挡重现等情况下漂移。以余弦距离为例，其表达式如下：
$\frac {f_{i} \cdot f_{j}} {\| f_{i} \| \| f_{j} \|}$
其中 $f_i$ , $f_j$ 分别为track历史特征和当前检测特征。

总体流程

检测输入与状态确认

DeepSORT的目标跟踪流程通常从外部检测器（如YOLOv5）输入每一帧的检测结果开始。这些检测框包含位置（中心点、宽高）等基本几何信息。每当新一帧检测到“未被分配到现有轨迹”的高置信度检测框时，DeepSORT会以此初始化一个新轨迹（Track）。此时，这条轨迹会被标记为未确认状态，系统不会立即将其纳入“有效”目标，而是需要持续验证其真实性。只有当一个未确认轨迹在连续若干帧内（通常设置为3）都被成功匹配到新的检测框，系统才会将其状态升级为已确认。这意味着目标必须表现出一定的持续性，才能避免由偶发噪声引发ID分裂或误报。通过这种方式，DeepSORT能有效过滤孤立、短暂的虚假检测。

轨迹预测

对于视频流中的每一帧，DeepSORT会先对当前所有轨迹利用卡尔曼滤波进行状态预测。具体来说，每个轨迹的状态向量（如位置、宽高、宽高比、速度等）会根据上帧状态和运动模型，计算出当前帧的“预测位置”，同时更新当前的协方差矩阵。这一步骤能够为后续检测框匹配提供空间位置的先验参考，还能在检测器短暂漏检、目标短时遮挡时，通过运动模型维持轨迹的连贯性，防止目标丢失。

级联匹配-代价矩阵获取

在级联匹配（Cascade Matching）的数据关联阶段，首先需要为每一个“已确认（Confirmed）”轨迹与所有当前检测结果建立匹配代价矩阵。代价矩阵的构建过程融合了运动信息与外观特征，以最大限度提升匹配的准确性和鲁棒性。

首先，系统会遍历所有处于“已确认”状态的轨迹。针对每个轨迹，利用卡尔曼滤波器的预测结果，计算其预测位置与所有新一帧检测框之间的运动距离。运动距离常采用马氏距离（Mahalanobis Distance），能够结合协方差信息，度量目标在状态空间内的空间相似性。与此同时，DeepSORT还为每个检测框提取了外观特征向量（如128维ReID特征），并与轨迹维护的历史外观特征进行特征距离的计算，通常采用余弦距离等指标，衡量目标外观的一致性。这两部分距离信息会按照预设的权重进行加权融合，得到最终的综合代价矩阵。形式上可以表示为：
$Ci,j=λ1dmotion(i,j)+λ2dappearance(i,j)C_{i,j}=\lambda_1 d_{motion}\left(i,j\right) + \lambda_2 d_{appearance}\left(i,j\right)$
其中， $C_{i,j}$ 代表第i个已确认轨迹与第j个检测框之间的综合匹配代价， $λ1\lambda_1$ 、 $λ2\lambda_2$ 分别为运动与外观距离的权重系数。在此基础上，DeepSORT会进一步依据“失配帧数”对已确认轨迹进行排序。级联匹配按照排序结果依次处理，每层依次计算当前层轨迹与所有剩余检测框之间的代价矩阵。这种分层、递进式的代价矩阵获取方式确保了高置信度轨迹能够优先与最匹配的检测框关联，大大降低了误匹配和ID切换的风险，为后续全局最优分配（即匈牙利算法）打下基础。

级联匹配-全局最优关联

在获取到代价矩阵后，DeepSORT利用匈牙利算法（Hungarian Algorithm）对所有已确认轨迹与检测框进行全局一对一分配。算法本质上是在二分图中，找到总代价最小的完全匹配。具体流程为：以轨迹为行，检测框为列，利用综合代价矩阵作为权重输入匈牙利算法，输出每个轨迹与检测框的最优匹配关系。每条轨迹最多只会被分配到一个检测框，每个检测框也最多只被分配到一条轨迹，实现全局唯一、无冲突的最优分配。这种做法能最大程度地降低整体关联误差，防止一对多、多对一等混淆和错误关联，是实现多目标跟踪高准确率和稳定性的关键步骤。

状态更新与新轨迹管理

对于匹配到的轨迹，DeepSORT通过卡尔曼滤波的“更新”步骤，融合检测观测与预测状态，获得新的最优估计，并同步更新协方差、外观特征等信息。每条轨迹还会维护一个特征库（如最近100帧的ReID特征），以缓解光照、姿态等带来的特征漂移。对于未被匹配的检测结果，如果其置信度较高且符合新目标判定条件，则作为新轨迹被加入系统管理。与此同时，对于那些在连续多帧内都未被检测框匹配到的确认状态轨迹，DeepSORT会记录其失配帧数（空帧数）。如果某条轨迹的空帧数超过了预设的最大允许值（如max_age），系统就会删除该轨迹。而非确认状态的轨迹如果没匹配成功，则会直接被删除。