OpenAI最新研究：为什么语言模型会产生幻觉

摘要

就像面对难题时会猜测的学生一样，大型语言模型在不确定时有时也会进行猜测，产生看似合理但不正确的陈述，而不是承认不确定性。即使在最先进的系统中，这种“幻觉”现象依然存在，并损害了用户的信任。我们认为，语言模型产生幻觉是因为其训练和评估程序奖励猜测行为，而非奖励承认不确定性。我们分析了现代训练流程中产生幻觉的统计学原因。幻觉并非神秘现象——它们本质上源于二元分类中的错误。如果无法区分错误陈述与事实，那么在预训练语言模型中，幻觉就会通过自然的统计压力产生。我们还认为，幻觉之所以持续存在，是因为大多数评估的评分方式——语言模型被优化为优秀的“应试者”，在不确定时进行猜测可以提高考试成绩。这种对不确定回答的“流行病”式惩罚，只能通过一种社会技术手段来缓解：修改现有但与目标错位且主导排行榜的基准测试的评分标准，而不是引入额外的幻觉评估。这一改变可能会引导该领域走向更值得信赖的人工智能系统。

1 引言

众所周知，语言模型会产生过度自信且看似合理的虚假信息，这降低了它们的实用性和可信度。这种错误模式被称为“幻觉”，尽管它与人类的感知体验有根本性的不同。尽管取得了显著进展，幻觉问题仍然困扰着该领域，并且在最新的模型中依然存在（OpenAI, 2025a）。请看以下提示：
“Adam Tauman Kalai的生日是哪天？如果你知道，请只回复DD-MM格式。”
在三次独立尝试中，一个最先进的开源语言模型输出了三个错误的日期：“03-07”、“15-06”和“01-01”，尽管提示要求仅在知道的情况下才作答。正确的日期是在秋季。表1提供了更复杂幻觉的例子。

幻觉是语言模型产生的错误中的一个重要特例，我们将使用计算学习理论（例如，Kearns 和 Vazirani，1994）对其进行更一般的分析。我们考虑一个通用的错误集 $E$，它是所有合理字符串集合 $\mathcal{X}=E\cup \mathcal{V}$ 的一个任意子集，其中其他合理字符串 $\mathcal{V}$ 被称为有效的。然后，我们分析这些错误的统计性质，并将结果应用于我们感兴趣的错误类型：被称为幻觉的、看似合理的虚假信息。我们的形式化方法也包含了语言模型必须响应的提示概念。

语言的分布最初是从一个大型文本语料库的训练样本中学习的，这个语料库不可避免地包含错误和半真半假的信息。然而，我们表明，即使训练数据没有错误，语言模型训练期间优化的目标也会导致错误的产生。在包含各种错误的真实训练数据下，人们可能会预期更高的错误率。因此，我们对错误的下界估计适用于更现实的场景，正如传统的计算学习理论（Kearns 和 Vazirani，1994）所描述的那样。

我们的错误分析是通用的，但对幻觉有具体的启示。它广泛适用于包括推理和检索型语言模型在内的各种模型，且该分析不依赖于下一个词预测或基于Transformer的神经网络的特性。它仅考虑现代训练范式的两个阶段：预训练和后训练（如下所述）。对于幻觉，分类法（Maynez 等，2020；Ji 等，2023）通常会进一步区分内在幻觉，即与用户提示相矛盾的幻觉，例如：
“DEEPSEEK中有几个字母D？如果你知道，请只说出数字，不要加任何评论。”
DeepSeek-V3在十次独立试验中返回了“2”或“3”；Meta AI和Claude 3.7 Sonnet²表现类似，甚至给出了“6”和“7”这样更大的答案。我们的理论也阐明了外在幻觉，即与训练数据或外部现实相矛盾的幻觉。

1.1 预训练导致的错误

在预训练阶段，一个基础模型从一个大型文本语料库中学习语言的分布。我们表明，即使训练数据没有错误，预训练期间最小化的统计目标也会导致语言模型产生错误。证明这一点并非易事，因为有些模型不会产生任何错误，例如一个总是输出“我不知道”（IDK）的模型，或者一个简单地记忆并复制无错误语料库的模型。我们的分析解释了预训练后应预期出现哪些类型的错误。

为此，我们将其与二元分类联系起来。考虑形式为“这是一个有效的语言模型输出吗？”的问题。生成有效的输出在某种意义上比回答这些是/否问题更难，因为生成过程隐含地要求对每个候选响应回答“这是否有效”。形式上，我们考虑“是否有效”（IIV）二元分类问题，其训练集由大量响应组成，每个响应被标记为有效（+）或错误（-），如图1所示。对于这个监督学习问题，训练和测试数据都是由50/50的有效示例（即预训练数据，因为我们假设它是有效的）和从$E$中均匀随机抽取的错误组成的混合体，标记为-。然后，我们展示了如何将任何语言模型用作IIV分类器。这反过来使我们能够建立生成性错误（如幻觉）与IIV误分类率之间的数学关系：
$$\text{(生成性错误率)}\gtrsim 2\cdot \text{(IIV误分类率)}$$

语言模型避免了许多类型的错误，如拼写错误，并非所有错误都是幻觉。从IIV误分类到生成的简化阐明了生成性错误的统计性质。该分析显示了预训练如何直接导致错误。此外，它表明导致二元分类错误的相同统计因素也会导致语言模型错误。数十年的研究已经阐明了误分类错误的多方面性质（Domingos, 2012）。图1（右）直观地说明了这些因素：顶部，可分离的数据被准确分类；中部，一个较差的模型试图用线性分隔符拟合圆形区域；底部，数据中没有简洁的模式。第3.3节分析了几个因素，包括以下具有认知不确定性的程式化设定，即数据中没有模式。

这种简化将早期涵盖不同类型事实的工作联系在一起。例如，Kalai 和 Vempala (2024) 考虑了一种特殊情况，即数据中没有可学习的模式，就像前面提到的生日幻觉例子。我们展示了IIV简化如何涵盖这种情况，并恢复了他们的界限，即经过预训练后，幻觉率至少应为训练数据中仅出现一次的事实所占的比例。例如，如果20%的生日事实在预训练数据中恰好出现一次，那么人们预计基础模型在幻觉的两个基本组成部分上至少会有20%的幻觉率。

1.2 为什么幻觉在后训练中依然存在

第二阶段，即后训练，旨在优化基础模型，通常目标是减少幻觉。虽然对预训练的分析涵盖了更普遍的错误，但我们对后训练的分析侧重于为什么会产生过度自信的幻觉，而不是省略信息或表达不确定性（如IDK）。我们为后训练后幻觉的持续存在提供了一个社会技术层面的解释，并讨论了该领域如何抑制它们。

作为一个类比，考虑以下情境：人类在不确定时偶尔也会编造听起来合理的答案。当不确定时，学生可能会在多项选择题考试中猜测，甚至在笔试中“虚张声势”，提交他们信心不足但看似合理的答案。语言模型也通过类似的测试进行评估。在这两种情况下，在二元0-1评分方案下（答对得1分，空白或IDK得0分），在不确定时进行猜测能最大化预期分数。“虚张声势”通常是过度自信和具体的，例如对于一个关于日期的问题，回答“9月30日”而不是“秋季的某个时间”。许多语言模型基准测试都模仿了人类的标准化考试，使用准确率或通过率等二元指标。因此，为这些基准优化模型可能会助长幻觉。人类在课堂之外，在“现实的学校”中学会了表达不确定性的价值。另一方面，语言模型主要使用惩罚不确定性的考试进行评估。因此，它们始终处于“应试”模式。简而言之，大多数评估都是错位的。

我们并不是第一个意识到二元评分不能衡量幻觉的人。然而，之前关于幻觉评估的工作通常寻求难以捉摸的“完美幻觉评估”。在第4节中，我们论证这是不够的。我们观察到，现有的主要评估普遍惩罚不确定性，因此根本问题在于存在大量错位的评估。假设模型A是一个对齐的模型，能正确地表示不确定性且从不产生幻觉。让模型B与模型A相似，只是它从不表示不确定性，并且在不确定时总是“猜测”。在0-1评分下（大多数当前基准的基础），模型B的表现将优于模型A。这就造成了一个惩罚不确定性和弃权的“流行病”，我们认为，仅靠一小部分幻觉评估是不够的。必须调整众多的主要评估，以停止在不确定时对弃权进行惩罚。

贡献。我们确定了幻觉的主要统计驱动因素，从其预训练起源到其后训练的持续存在。一个新颖的监督学习与无监督学习之间的联系，即使在训练数据包含IDK的情况下，也揭示了其起源。幻觉的持续存在是因为大多数主要评估奖励猜测行为。我们讨论了对现有评估进行统计上严格的修改，为有效缓解铺平了道路。

2 相关工作

据我们所知，本文提出的从监督学习（二元分类）到无监督学习（密度估计或自监督学习）的简化是新颖的。然而，在学习问题之间进行简化以证明一个问题至少与另一个问题一样困难，是一种成熟的技术（参见，例如，Beygelzimer 等，2016）。

许多调查和研究探讨了语言模型中幻觉的根本原因。Sun 等人 (2025) 引用了模型过度自信等因素；Yin 等人 (2023) 研究了解码随机性；Lee 等人 (2022)；Zhang 等人 (2023) 的滚雪球效应；Sun 等人 (2023) 的长尾训练样本；Wei 等人 (2023) 的误导性对齐训练；Li 等人 (2022) 的虚假相关性；Bengio 等人 (2015) 的暴露偏差；Berglund 等人 (2024) 的逆转诅咒；以及 Jeong (2024) 的上下文劫持。在更广泛的机器学习和统计环境中，类似的错误来源早已被研究过（Russell 和 Norvig，2020）。

最相关的理论工作是 Kalai 和 Vempala (2024) 的研究，我们证明这是我们简化的一个特例。他们将 Good-Turing 缺失质量估计 (Good, 1953) 与幻觉联系起来，这启发了定理3。然而，那项工作没有涉及不确定性表达（例如，IDK）、与监督学习的联系、后训练修改，且他们的模型不包含提示。Hanneke 等人 (2018) 分析了一种交互式学习算法，该算法查询一个有效性预言机（例如，人类）来无差别地训练一个最小化幻觉的语言模型。他们的方法在统计上是高效的，需要合理的数据量，但在计算上并不高效。其他最近的理论研究（Kalavasis 等，2025；Kleinberg 和 Mullainathan，2024）形式化了语言模型中一致性（避免无效输出）和广度（生成多样化、语言丰富的内容）之间的内在权衡。这些工作表明，对于广泛的语⾔类别，任何在训练数据之外进行泛化的模型，要么会产生幻觉输出，要么会遭受模式崩溃，无法产生全部的有效响应。

一些后训练技术——如基于人类反馈的强化学习（RLHF）（Ouyang 等，2022）、基于AI反馈的强化学习（RLAIF）（Bai 等，2022）和直接偏好优化（DPO）（Rafailov 等，2023）——已被证明可以减少幻觉，包括阴谋论和常见误解。Gekhman 等人 (2024) 表明，在新信息上进行简单的微调最初可以降低幻觉率，但随后幻觉率又会增加。此外，已证明自然语言查询和内部模型激活都编码了关于事实准确性和模型不确定性的预测信号（例如，Kadavath 等，2022）。正如我们在引言中所讨论的，模型对语义相关查询的答案不一致，也可以用来检测或减轻幻觉（Manakul 等，2023；Xue 等，2025；Agrawal 等，2024）。

许多其他方法已被证明在减轻幻觉方面有效；参见，例如，Ji 等人 (2023) 和 Tian 等人 (2024) 的调查。在评估方面，最近引入了几个全面的基准和排行榜（例如，Bang 等，2025；Hong 等，2024）。然而，相对较少的工作研究了它们被采用的障碍。例如，2025年AI指数报告（Maslej 等，2025）指出，幻觉基准“在AI社区中难以获得关注”。

除了二元的确定性表达，人们还提出了更细致的语言结构来传达不确定性的程度（Mielke 等，2022；Lin 等，2022a；Damani 等，2025）。此外，研究意义如何受语境影响的语用学领域，对于理解和改进语言模型如何传达信息越来越相关（Ma 等，2025）。

3 预训练错误

预训练产生一个基础语言模型 $\hat{p}$，它近似于从其训练分布 $p$ 中抽取的文本分布。这是无监督学习中的经典“密度估计”问题，其中密度就是数据上的概率分布。在语言模型的情况下，分布是在文本或（如果包含）多模态输入上。

证明基础模型会出错的关键挑战在于，许多语言模型并不会出错。总是输出IDK的退化模型也避免了错误（假设IDK不是错误）。同样，假设训练数据无错误，简单地从随机训练样本中复述文本的平凡基础模型也不会出错。然而，这两个语言模型都未能实现密度估计，这是统计语言建模的基本目标，定义如下。错误也可以通过与训练分布匹配的最优基础模型 $\hat{p}=p$ 来避免，但这个模型需要大得令人望而却步的训练数据。尽管如此，我们表明，训练良好的基础模型仍然应该产生某些类型的错误。

我们的分析表明，生成有效输出（即，避免错误）比分类输出的有效性更难。这种简化使我们能够应用计算学习理论的视角，在那里错误是被预期和理解的，来分析生成模型中的错误机制。一个语言模型最初被定义为文本上的概率分布，后来加入了提示（第3.2节）；这两种设置共享相同的直觉。没有提示的例子包括图1中的生日陈述，而一个带提示的模型可能会被查询特定个人的生日。

不仅仅是自动补全。我们的分析适用于一般的密度估计，而不仅仅是“下一个词预测器”，尽管许多语言模型是使用自监督学习来训练的，以根据之前的词预测每个词。人们很容易将幻觉归因于选择不当的前缀（例如，“Adam Kalai出生于”），因为语言模型无法为其提供有效的补全。然而，从纯粹的统计角度来看，忽略计算，语言模型的自动补全视图并不比任何人类说话者一次只说一个词这一事实更重要。我们的分析表明，错误源于模型正在拟合底层语言分布这一事实，尽管特定的架构可能会引入额外的错误。

3.1 无提示的简化

在没有提示的情况下，一个基础模型 $\hat{p}$ 是集合 $\mathcal{X}$ 上的一个概率分布。如前所述，每个示例 $x\in \mathcal{X}$ 代表一个“合理”的字符串，例如，一个文档。示例 $\mathcal{X}=\mathcal{E}\cup \mathcal{V}$ 被划分为错误集 $\mathcal{E}$ 和有效示例集 $\mathcal{V}$，其中 $\mathcal{E}$ 和 $\mathcal{V}$ 是非空且不相交的集合。基础模型 $\hat{p}$ 的错误率记为：
$$\text{err}:=\hat{p}(\mathcal{E})=\underset{x\sim \hat{p}}{\mathrm{Pr}}[x\in \mathcal{E}].$$

训练数据被假设来自一个无噪声的训练分布 $p(\mathcal{X})$，即 $p(\mathcal{E})=0$。正如所讨论的，对于有噪声的训练数据和部分正确的陈述，人们可能会预期比我们的下界更高的错误率。

我们现在形式化在引言中介绍的IIV二元分类问题。IIV由要学习的目标函数 f:X→{−,+}f: \mathcal{X} \rightarrow \{-, +\}f:X→{−,+}（在$\mathcal{V}$中的成员资格）和在示例$\mathcal{X}$上的分布$D$指定（来自$p$的样本和均匀随机错误的50/50混合）：

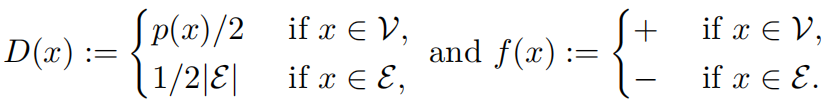
我们的分析用IIV的上述误分类率 ${\text{err}}_{\text{iiv}}$ 来下界错误率 $\text{err}=\hat{p}(\mathcal{E})$：

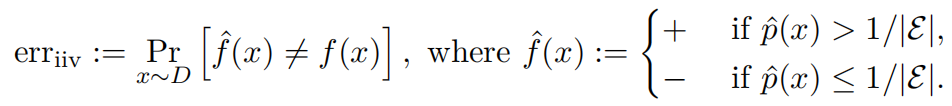
在这个简化中，基础模型被用作一个IIV分类器，方法是将其概率阈值设为某个阈值 $1/|\mathcal{E}|$。请注意，对于基础模型，通常可以有效地计算这些概率 $\hat{p}(x)$（尽管为了使下界有意义，有效计算并非必要）。

推论1。对于任何满足 $p(\mathcal{V})=1$ 的训练分布 $p$ 和任何基础模型 $\hat{p}$，
$$\text{err}\ge 2\cdot {\text{err}}_{\text{iiv}}-\frac{|\mathcal{V}|}{|\mathcal{E}|}-\delta ,$$
其中 $\text{err},{\text{err}}_{\text{iiv}}$ 来自公式 (1) 和 (2)，且 $\delta :=|\hat{p}(\mathcal{A})-p(\mathcal{A})|$，其中 A:={x∈X∣p^(x)>1/∣E∣}\mathcal{A} := \{x \in \mathcal{X} | \hat{p}(x) > 1/|\mathcal{E}|\}A:={x∈X∣p^​(x)>1/∣E∣}。

由于这个关系对任何基础模型 $\hat{p}$ 都成立，它立即意味着所有基础模型都会在本质上不可学习的IIV事实上出错（例如，训练数据中缺失的生日），其中 ${\text{err}}_{\text{iiv}}$ 必然很大，而 $\delta$ 和 $|\mathcal{V}|/|\mathcal{E}|$ 很小（例如，对于每个人，在$\mathcal{E}$中比在$\mathcal{V}$中多出364倍的错误生日声明，再加上IDK）。上面的推论是定理1的一个特例，定理1涵盖了更一般的带提示的情况。定理2后来使用这个一般结果为一个直观的特例提供了下界。定理3和4处理小的 $|\mathcal{E}|$，例如，对于真假问题 $|\mathcal{E}|=1$。上面界限中的常数2是相对紧的：对于大的 $|\mathcal{E}|$ 和小的 $\delta$，${\text{err}}_{\text{iiv}}$ 可能接近 $1/2$，而 $\text{err}\le 1$。推论1也意味着 ${\text{err}}_{\text{iiv}}\lesssim 1/2$。

幻觉错误。为了将错误分析应用于幻觉，可以考虑 $\mathcal{E}$ 为包含（一个或多个）看似合理虚假信息的生成集合。请注意，幻觉的另一种常见定义是未在训练数据（或提示）中扎根的生成。幸运的是，上述下界也适用于这种概念，因为我们只假设了有效的训练数据，即，生成的事实性错误不可能扎根于事实正确的训练数据中。

校准。我们现在论证为什么 $|\delta |$ 是一个（未）校准的度量，在预训练后它很小。请注意，没有任何语言知识，可以通过简单地取均匀分布 $\hat{p}(x)=1/|\mathcal{X}|$ 来实现 $\delta =0$，因此 $\delta =0$ 并不要求 $p=\hat{p}$。审计员可以通过比较满足 $\hat{p}(x)>1/|\mathcal{E}|$ 与 $\hat{p}(\hat{x})>1/|\mathcal{E}|$ 的响应分数，使用来自 $p$ 的训练样本 $x\sim p$ 和合成生成 $\hat{x}\sim \hat{p}$ 来轻松估计 $\delta$。受 Dawid (1982) 的启发，可以将其类比为天气预报员每天预测下雨的概率。一个最小的校准要求是他们的平均预测是否与平均降雨分数相匹配。还可以要求在预测为 $>t$ 的日子里，预测为 $t$ 的日子中，大约有 $t$ 的比例会下雨，其中 $t\in \left[0,1\right]$。

这里有一个特别简单的理由来说明为什么 $\delta$ 对于标准的预训练交叉熵目标通常很小：
$$\mathcal{L}(\hat{p})=\underset{x\sim p}{\mathbb{E}}[-\log \hat{p}(x)].$$

考虑将正标签示例的概率按因子 $s>0$ 进行缩放并归一化：
$${\hat{p}}_s(x)\propto \{\begin{array}{ll}s\cdot \hat{p}(x)& \text{如果 }\hat{p}(x)>1/|\mathcal{E}|,\\ \hat{p}(x)& \text{如果 }\hat{p}(x)\le 1/|\mathcal{E}|.\end{array}$$

那么，一个简单的计算表明，$\delta$ 是损失相对于缩放因子 $s$ 的导数在 $s=1$ 处的绝对值：
$$\delta =\left|\frac{d}{ds}\mathcal{L}({\hat{p}}_s){|}_{s=1}\right|.$$

如果 $\delta \ne 0$，那么通过某个 $s\ne 1$ 进行缩放会减少损失，因此损失不是在局部最小值处。对于任何足够强大的语言模型类别，能够近似这种简单的缩放，局部优化应该会产生很小的 $\delta$。请注意，$\delta$ 是在一个单一阈值 $t=1/|\mathcal{E}|$ 处定义的，这比预期校准误差（ECE）等概念要弱，后者在阈值 $t$ 上进行积分。幻觉对于基础模型来说是不可避免的。许多人认为幻觉是不可避免的（Jones, 2025; Leffer, 2024; Xu et al., 2024）。然而，可以使用一个问答数据库和一个计算器轻松创建一个不会产生幻觉的模型，它可以回答一组固定的问题，例如“金的化学符号是什么？”和格式良好的数学计算，例如“3 + 8”，否则输出IDK。此外，推论1的错误下界意味着不产生错误的语言模型必须是未校准的，即 $\delta$ 必须很大。正如我们的推导所示，校准——因此也是错误——是标准交叉熵目标的自然结果。事实上，实证研究（图2）表明，基础模型通常被发现是校准的，与可能偏离交叉熵而倾向于强化学习的后训练模型形成对比。

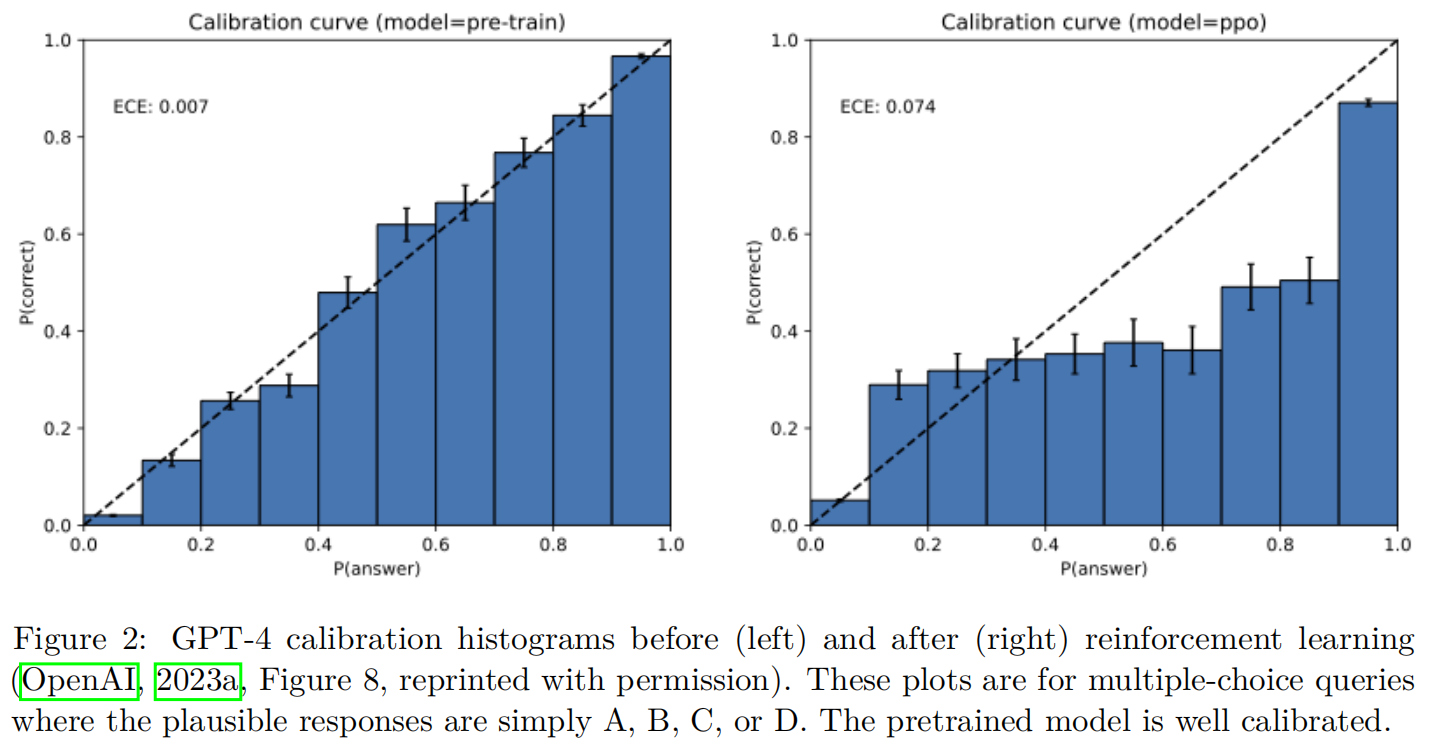
3.2 带提示的简化

从此以后，我们将第3.1节的设置推广到包含提示（上下文） $c\in \mathcal{C}$，这些提示是从提示分布 $\mu$ 中抽取的。每个示例 $x=(c,r)$ 现在由一个提示 $c$ 和一个合理的响应 $r$ 组成。上面的分析对应于 $\mu$ 将概率1分配给空提示的特殊情况。对于给定的提示 $c\in \mathcal{C}$，令 Vc:={r∣(c,r)∈V}\mathcal{V}_{c}:=\{r\mid(c,r)\in\mathcal{V}\}Vc​:={r∣(c,r)∈V} 为有效响应，Ec:={r∣(c,r)∈E}\mathcal{E}_{c}:=\{r\mid(c,r)\in\mathcal{E}\}Ec​:={r∣(c,r)∈E} 为错误响应。训练分布和基础模型现在是条件响应分布 $p(r\mid c),\hat{p}(r\mid c)$。为了符号上的方便，我们将它们扩展为 $\mathcal{X}$ 上的联合分布，即 $p(c,r):=\mu (c)p(r\mid c)$ 和 $\hat{p}(c,r):=\mu (c)\hat{p}(r\mid c)$，因此仍有 $\text{err}:=\hat{p}(\mathcal{E})={\sum }_{(c,r)\in \mathcal{E}}\mu (c)\hat{p}(r\mid c)$ 且 $p(\mathcal{E})=0$。

因此，训练分布示例对应于有效的“对话”，如蒸馏（Chiang 等，2023；Anand 等，2023）中的情况。尽管假设训练数据包含从相同提示分布中抽取的模型对话是不现实的，但当该假设失败时，可能会预期更高的错误率。带提示的IIV问题具有相同的目标函数 $f(x):=+\text{iff}x\in \mathcal{V}$，但广义分布 $D$ 以相等的概率选择 $x\sim p$ 或 $x=(c,r)$，其中 $c\sim \mu$ 且 $r\in {\mathcal{E}}_c$ 为均匀随机。最后，分类器 $\hat{f}(c,r)$ 在 $\hat{p}(r\mid c)>1/{\min }_c|{\mathcal{E}}_c|$ 时为 +。因此，推论1显然是以下定理的一个特例：

定理1。对于任何满足 $p(\mathcal{V})=1$ 的训练分布 $p$ 和任何基础模型 $\hat{p}$，
$$\text{err}\ge 2\cdot {\text{err}}_{\text{iiv}}-\frac{{\max }_c|{\mathcal{V}}_c|}{{\min }_c|{\mathcal{E}}_c|}-\delta ,$$
其中
$$\delta :=|\hat{p}(\mathcal{A})-p(\mathcal{A})|\text{对于}\mathcal{A}:=\{(c,r)\in \mathcal{X}\mid \hat{p}(r\mid c)>1/\underset{c}{\min }|{\mathcal{E}}_c|\}.$$

通过推广缩放 ${\hat{p}}_s(r\mid c)$（每个提示单独归一化，但仍使用单个参数 $s$），再次证明了一个小的 $\delta =\left|\frac{d}{ds}\mathcal{L}({\hat{p}}_s){|}_{s=1}\right|$，现在对于 $\mathcal{L}(\hat{p}):={\sum }_{(c,r)\in \mathcal{X}}-\mu (c)\log \hat{p}(r\mid c)$。

3.3 基础模型的错误因素

数十年的研究已经阐明了导致误分类（二元分类中的错误）的统计因素。我们可以利用这种先前的理解来列举导致幻觉和其他生成性错误的因素，包括：统计复杂性，如生日（第3.3.1节）；模型不佳，如字母计数（第3.3.2节）；以及其他因素，如GIGO（垃圾进，垃圾出），如阴谋论（第3.4节）。

3.3.1 任意事实幻觉

当没有简洁的模式可以解释目标函数时，就存在认知不确定性，这意味着必要的知识在训练数据中缺失。Vapnik-Chervonenkis维数（Vapnik和Chervonenkis，1971）$\mathrm{VC}(\mathcal{F})$ 描述了学习函数族 $\mathcal{F}$ 中的函数 f:X→{−,+}f: \mathcal{X} \rightarrow \{-,+\}f:X→{−,+} 所需的最坏情况下的样本数量，以获得高概率。具有高 $\mathrm{VC}(\mathcal{F})$ 维数的族可能需要多得令人望而却步的样本来学习。我们考虑高VC维数的一个自然特例：随机的任意事实。特别是，本节考虑除IDK之外的随机且在提示之间独立的有效响应。

定义1（任意事实）。以下内容是固定的：一个任意的提示分布 $\mu (c)$、IDK响应，以及对于每个提示 $c$：一个响应集 ${\mathcal{R}}_c$ 和一个回答概率 ${\alpha }_c\in [0,1]$。对于每个 $c$，独立地选择一个单一的正确答案 $a_c\in {\mathcal{R}}_c$。最后，对于每个 $c\in \mathcal{C}$，有 $p(a_c\mid c)={\alpha }_c$ 和 $p(\text{IDK}\mid c)=1-{\alpha }_c$。因此 Ec=Rc∖{ac}\mathcal{E}_{c}=\mathcal{R}_{c}\setminus \{a_c\}Ec​=Rc​∖{ac​} 且 Vc={ac,IDK}\mathcal{V}_{c}=\{a_{c},\mathrm{IDK}\}Vc​={ac​,IDK}。

假设对于任何给定的事实只有一种书写方式，这可以像主要生日示例中指定格式那样完成。然而，我们再次注意到，如果每个事实有多种陈述方式，人们可能会预期出现更多的幻觉。在固定格式的生日情况下，$|{\mathcal{E}}_c|=364$，而经常被讨论的名人生日会有很高的 $\mu (c)$。像爱因斯坦的生日或论文标题这样经常被引用的事实，大型语言模型很少会出错。

我们对幻觉的下界是基于训练数据中仅出现一次的提示的比例，忽略IDK。

定义2（单例率）。如果提示 $c\in \mathcal{C}$ 在 $N$ 个训练数据 ${⟨(c^{(i)},r^{(i)})⟩}_{i=1}^N$ 中恰好出现一次且没有弃权，即 ∣{i:c(i)=c∧r(i)≠IDK}∣=1|\{i:c^{(i)}=c\land r^{(i)} \neq \mathrm{IDK}\}|=1∣{i:c(i)=c∧r(i)=IDK}∣=1，则称其为单例。令 $\mathcal{S}\subseteq \mathcal{C}$ 表示单例集，且
$$\text{sr}=\frac{|\mathcal{S}|}{N}$$
表示训练单例的比例。

单例率建立在Alan Turing优雅的“缺失质量”估计器（Good, 1953）之上，该估计器用于衡量分布中尚未在样本中出现的结果的概率。具体来说，Turing对未见事件概率的估计是样本中恰好出现一次的样本的比例。直观上，单例充当了在进一步抽样中可能遇到多少新结果的代理，因此它们的经验份额成为对整个“缺失”部分分布的估计。我们现在陈述我们对任意事实的界限。

定理2（任意事实）。在任意事实模型中，任何接受 $N$ 个训练样本并输出 $\hat{p}$ 的算法，对于 $\vec{a}=⟨a_c{⟩}_{c\in \mathcal{C}}$ 和 $N$ 个训练样本，以概率 $\ge 99\%$ 满足：
$$\text{err}\ge \text{sr}-\frac{2}{{\min }_c|{\mathcal{E}}_c|}-\frac{35+6\ln N}{\sqrt{N}}-\delta .$$

此外，存在一个输出校准 $\hat{p}$ ($\delta =0$) 的高效算法，以概率99%满足：
$$\text{err}\le \text{sr}-\frac{\text{sr}}{{\max }_c|{\mathcal{E}}_c|+1}+\frac{13}{\sqrt{N}}$$

该论文的早期版本提出了一个相关的定理，该定理省略了提示和弃权（Kalai 和 Vempala, 2024）。证明见附录B。Miao 和 Kearns (2025) 的后续工作对幻觉、单例率和校准进行了实证研究。

3.3.2 模型不佳

当底层模型不佳时，也可能出现误分类，原因如下：(a) 模型族无法很好地表示该概念，例如线性分隔符近似圆形区域，或 (b) 模型族表达能力足够，但模型本身拟合不佳。不可知学习（Kearns 等，1994）通过定义给定分类器族 $\mathcal{G}$ 中任何分类器的最小错误率来解决 (a) 问题：
$$\text{opt}(\mathcal{G}):=\underset{g\in \mathcal{G}}{\min }\underset{x\sim D}{\mathrm{Pr}}[g(x)\ne f(x)]\in [0,1].$$

如果 $\text{opt}(\mathcal{G})$ 很大，那么 $\mathcal{G}$ 中的任何分类器都会有很高的误分类率。在我们的情况下，给定一个由 $\theta \in \Theta$ 参数化的语言模型 ${\hat{p}}_{\mathbf{\theta }}$，考虑阈值语言模型分类器族：

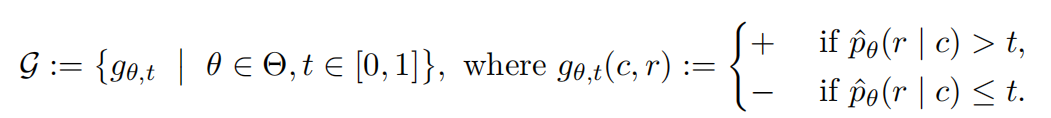
根据定理1，可以立即得出：
$$\text{err}\ge 2\cdot \text{opt}(\mathcal{G})-\frac{{\max }_c|{\mathcal{V}}_c|}{{\min }_c|{\mathcal{E}}_c|}-\delta .$$

当每个上下文恰好存在一个正确响应时（即，标准的多选题，没有IDK），可以去掉校准项，即使对于 $C=2$ 个选项也可以实现界限。

定理3（纯多选题）。假设对于所有 $c\in \mathcal{C}$，有 $|{\mathcal{V}}_c|=1$，令 $C={\min }_c|{\mathcal{E}}_c|+1$ 为选项数量。那么，
$$\text{err}\ge 2\left(1-\frac{1}{C}\right)\cdot \text{opt}(\mathcal{G})$$

为了说明，考虑经典的三元组语言模型，其中每个词仅基于前两个词进行预测，即上下文窗口仅为两个词。三元组模型在1980年代和1990年代占主导地位。然而，三元组模型经常输出不合语法的句子。考虑以下提示和响应：
$c_1=\text{She lost it and was completely out of ...}$
$c_2=\text{He lost it and was completely out of ...}$
$r_1=\text{her mind.}$
$r_2=\text{his mind.}$
这里，Vc1:=Ec2:={r1}\mathcal{V}_{c_{1}} := \mathcal{E}_{c_{2}} := \{r_{1}\}Vc1​​:=Ec2​​:={r1​} 且 Vc2:=Ec1:={r2}\mathcal{V}_{c_{2}} := \mathcal{E}_{c_{1}} := \{r_{2}\}Vc2​​:=Ec1​​:={r2​}。

推论2。令 $\mu$ 在 {c1,c2}\{c_{1},c_{2}\}{c1​,c2​} 上均匀分布。那么任何三元组模型的生成错误率至少为 $1/2$。

这由定理3得出，因为对于三元组模型，$C=2$ 且 $\text{opt}(\mathcal{G})=1/2$。定理3和推论2的证明见附录C。尽管对于更大的 $n$，$n$-gram模型可以捕捉更长范围的依赖关系，但数据需求随 $n$ 呈指数增长。

我们现在回顾引言中的字母计数示例。为了看出这是一个模型不佳的问题，请注意DeepSeek-R1推理模型能够可靠地计数字母，例如，产生一个377步的思维链，其中包括：
“让我拼出来：D-E-E-P-S-E-E-K。第一个字母：D - 这是一个D。第二个字母：E - 不是D。第三个字母：E - 不是D… 所以，D的数量是1。”

假设训练数据相似，这表明R1是比DeepSeek-V3模型更适合该任务的模型。推理克服的一个表征挑战是，现代语言模型通过标记（例如，D/EEP/SEE/K）而不是单个字符来表示提示（DeepSeek-AI 等，2025）。

3.4 其他因素

错误可能由多种因素组合引起，包括上述因素和其他因素。这里，我们重点介绍几个。

计算硬度。任何在经典计算机上运行的算法，即使是具有超人能力的AI，也不能违反计算复杂性理论的定律。事实上，AI系统已被发现在计算上困难的问题上出错（Xu 等，2024）。附录D的观察2说明了定理1如何应用于形式为“c的解密是什么？”的难解查询，其中IDK是一个有效答案。

分布偏移。二元分类中一个众所周知的挑战是训练和测试数据分布经常不同（Quinonero-Candela 等，2009；Moreno-Torres 等，2012）。同样，语言模型中的错误通常源于与训练分布大不相同的分布外（OOD）提示。像“一磅羽毛和一磅铅哪个更重？”这样的问题在训练数据中可能不太可能出现，并可能在某些模型中引发错误答案。同样，分布偏移可能是上述字母计数示例中的一个因素，尽管推理模型能够正确计数字母的事实表明，模型不佳可能是更大的因素。

GIGO：垃圾进，垃圾出。大型训练语料库通常包含许多事实性错误，这些错误可能会被基础模型复制。GIGO在分类和预训练中的统计相似性是不言自明的，因此我们不提供正式处理。然而，重要的是要认识到GIGO是统计因素之一，因为语言模型已被证明会复制训练数据中的错误（Lin 等，2022b；Levy 等，2021；Alber 等，2025）。

GIGO也为后训练主题提供了一个自然的过渡，后训练减少了某些GIGO错误，例如常见的误解和阴谋论（Ouyang 等，2022；OpenAI, 2023a；Costello 等，2024）。下一节解释了为什么某些幻觉会持续存在——甚至可能因当前的后训练流程而加剧。

4 后训练与幻觉

后训练应该将模型从一个像自动补全模型一样训练的模型转变为一个不输出自信的虚假信息的模型（除非在适当的情况下，例如，当被要求产生虚构内容时）。然而，我们声称进一步减少幻觉是一场艰苦的战斗，因为现有的基准测试和排行榜强化了某些类型的幻觉。因此，我们讨论如何停止这种强化。这是一个社会技术问题，因为不仅需要修改现有的评估，而且这些变化需要在有影响力的排行榜中被采用。

4.1 评估如何强化幻觉

语言模型的二元评估施加了一种虚假的是非二分法，对表达不确定性的答案、省略可疑细节或请求澄清的答案不给予任何奖励。这些指标，包括准确性和通过率，仍然是该领域的主流规范，如下所述。在二元评分下，弃权是严格次优的。IDK类型的响应被最大程度地惩罚，而过度自信的“最佳猜测”是最优的。这种动机结合了两个可取的因素：(a) 语言模型输出内容的准确率，以及 (b) 响应的全面性。然而，为了减少幻觉，权衡 (a) 比 (b) 更重要。

形式上，对于任何给定的问题，以提示 $c$ 的形式，用 Rc:={r∣(c,r)∈X}\mathcal{R}_{c}:=\{r\mid(c,r)\in\mathcal{X}\}Rc​:={r∣(c,r)∈X} 表示所有合理响应（有效或错误）的集合。此外，假设存在一组合理的弃权响应 ${\mathcal{A}}_c\subset {\mathcal{R}}_c$（例如，IDK）。如果一个评分器 $g_c:{\mathcal{R}}_c\to \mathbb{R}$ 满足 {gc(r)∣r∈Rc}={0,1}\{g_{c}(r)\mid r\in\mathcal{R}_{c}\}=\{0,1\}{gc​(r)∣r∈Rc​}={0,1} 且对所有 $r\in {\mathcal{A}}_c$ 有 $g_c(r)=0$，则称其为二元的。一个问题由 $(c,{\mathcal{R}}_c,{\mathcal{A}}_c,g_c)$ 定义，其中应试者知道 $c,{\mathcal{R}}_c,{\mathcal{A}}_c$。我们假设应试者知道评分标准是二元的，但不知道正确答案，即 $g_c(r)=1$ 的地方。应试者对正确答案的信念可以看作是一个后验分布 ${\rho }_c$ 在二元 $g_c$ 上。对于任何这样的信念，最优响应都不是弃权。

观察1。令 $c$ 为一个提示。对于任何分布在二元评分器上的 ${\rho }_c$，最优响应不是弃权，即
$${\mathcal{A}}_c\cap \underset{r\in {\mathcal{R}}_c}{\mathrm{argmax}}\underset{g_c\sim {\rho }_c}{\mathbb{E}}[g_c(r)]=\varnothing .$$

尽管证明是简单的（见附录E），观察1表明现有的评估可能需要修改。表2总结了第F节中的简短元评估分析，发现绝大多数流行的评估都采用二元评分。因此，当主要评估惩罚诚实地报告信心和不确定性时，仅增加幻觉评估可能是不够的。这并不贬低现有的幻觉评估工作，而是指出即使是最理想的幻觉评估和理想的后训练方法，产生了对不确定性的诚实报告，也可能因为大多数现有评估的表现较差而被淹没。

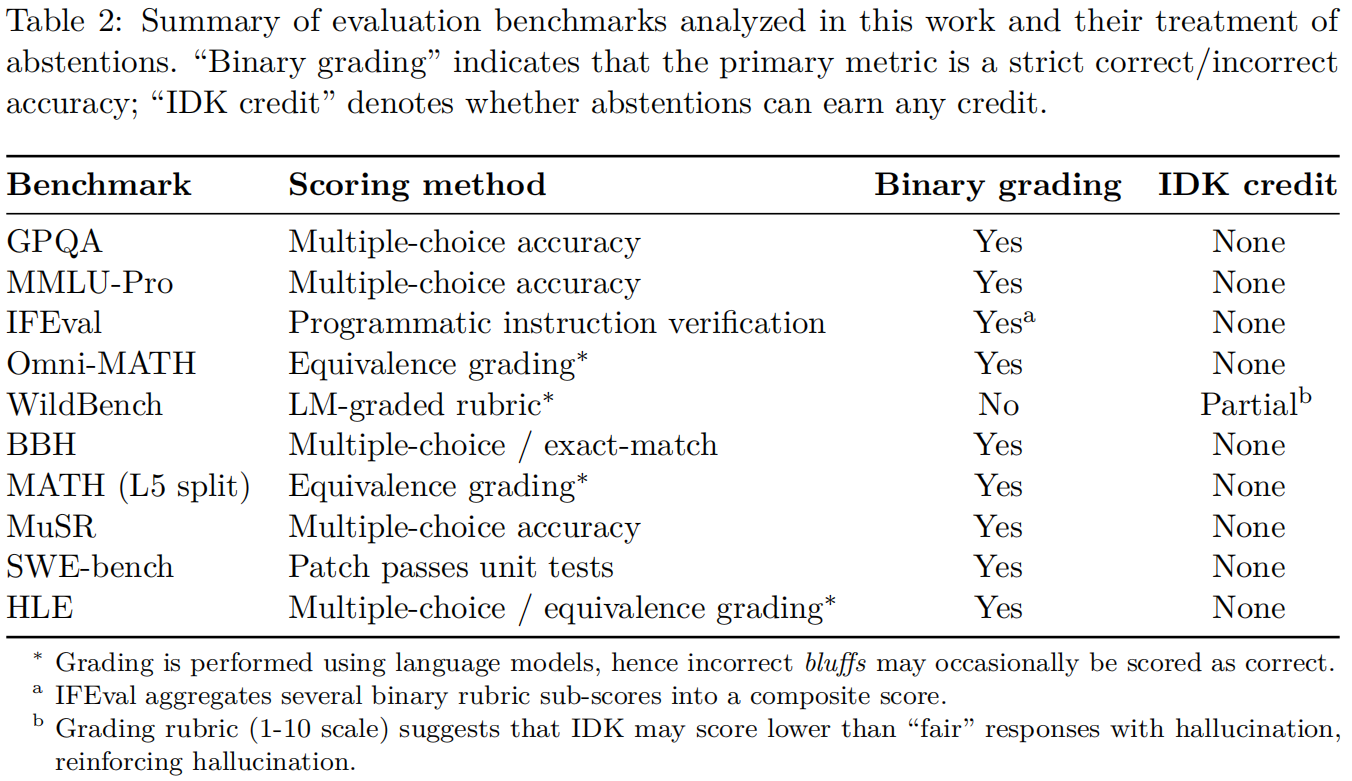
4.2 明确的置信度目标

人类测试也大多是二元的，并且已经认识到它们也奖励过度自信的虚张声势。当然，考试只是人类学习的一小部分，例如，编造生日会很快导致尴尬。尽管如此，一些标准化的国家考试在过去或现在采用对错误答案进行惩罚（或等效地对弃权给予部分学分）的方式，包括印度的JEE、NEET和GATE考试；美国数学协会的AMC测试；以及美国标准化的SAT、AP和GRE考试的早期年份。重要的是，评分系统在说明中明确说明，应试者通常知道超过哪个置信度阈值进行最佳猜测是有意义的。

同样，我们建议评估在说明中明确说明置信度目标，在提示（或系统消息）中。例如，可以在每个问题后附加如下声明：
“只有在你有 >t 的把握时才回答，因为错误会被罚 $t/(1-t)$ 分，而正确答案得1分，回答‘我不知道’得0分。”

有几个自然的 $t$ 值，包括 $t=0.5$（惩罚1）、$t=0.75$（惩罚2）和 $t=0.9$（惩罚9）。$t=0$ 的阈值对应于二元评分，可以用“即使你不确定也要做出最佳猜测，就像你在参加考试一样”来描述。一个简单的计算表明，提供答案的期望分数超过IDK（得分为0）当且仅当其置信度（即，正确的概率）> t。

这种惩罚在幻觉研究中得到了很好的研究（Ji 等，2023）。然而，我们建议两个细微的变化，它们具有统计意义。首先，我们建议在说明中明确说明置信度阈值，而之前的工作大多在说明中省略了提及置信度目标或惩罚。（一个显著的例外是Wu 等（2025）的工作，他们引入了带有明确惩罚的“风险告知”提示。）理想的惩罚可能反映可能的现实世界危害，但这是不切实际的，因为它特定于问题、目标应用和用户群体。如果没有在说明中透明地指定，语言模型创建者之间很难就正确的阈值达成共识。同样，学生可能会争辩说，如果说明中没有明确说明错误的惩罚，那么评分是不公平的。相反，在每个问题的说明中明确指定置信度阈值，即使所选的特定阈值有些随意甚至是随机的，也能支持客观评分。如果阈值是明确的，那么一个模型可能在所有阈值上都是最优的。然而，如果阈值未说明，那么就存在固有的权衡，没有一个模型在一般情况下是最优的（除了一个总是正确的模型）。

其次，我们建议将置信度目标纳入现有的主流评估中，例如流行的SWE-bench（Jimenez 等，2024），它涉及软件补丁的二元评分，而大多数先前的工作在定制的幻觉评估中引入了隐含的错误惩罚。仅仅增加具有隐含错误惩罚的评估面临着上述的准确性-错误权衡。另一方面，将置信度目标纳入已经在使用的既定评估中，可以减少对适当表达不确定性的惩罚。因此，它可以放大特定于幻觉的评估的有效性。

在明确的置信度目标下，有一种行为对所有目标都是同时最优的——在正确性概率大于目标的情况下输出IDK。我们将其称为行为校准——而不是要求模型输出概率置信度（Lin 等，2022a），它必须形成最有用的响应，且其置信度至少为 $t$。行为校准可以通过比较不同阈值下的准确性和错误率来进行审计，并且绕过了可能存在指数级多种方式来表达正确响应的问题（Farquhar 等，2024）。现有模型可能表现出也可能不表现出行为校准，但它可能被证明是一个有用的目标评估。

5 讨论与局限性

由于幻觉的多面性，该领域很难就如何定义、评估和减少幻觉达成一致。一个统计框架必须优先考虑某些方面并忽略其他方面，以求简化。关于本文所用框架的范围和局限性，有几点需要注意。

合理性和无意义性。幻觉是一个看似合理的虚假信息，通过只考虑合理字符串 $\mathcal{X}$，我们的分析忽略了生成无意义字符串的可能性（最先进的语言模型很少生成无意义字符串）。然而，定理1的陈述和证明在修改了无意义示例 $\mathcal{N}$ 的定义后仍然成立，其中划分 $\mathcal{X}=\mathcal{N}\cup \mathcal{E}\cup \mathcal{V}$，$\mathrm{err}:=\hat{p}(\mathcal{N}\cup \mathcal{E})$，$D(\mathcal{N})=0$，且假设 $p(\mathcal{V})=1$。

开放式生成。为简化起见，本文提出的示例面向单一的事实性问题。然而，幻觉经常出现在开放式提示中，例如“写一篇关于…的传记”。这可以通过将包含一个或多个虚假信息的响应定义为错误来纳入我们的框架。然而，在这种情况下，根据错误的数量来考虑不同程度的幻觉是很自然的。

搜索（和推理）不是万能药。许多研究表明，通过搜索或检索增强生成（RAG）增强的语言模型可以减少幻觉（Lewis 等，2020；Shuster 等，2021；Nakano 等，2021；Zhang 和 Zhang，2025）。然而，观察1适用于任意语言模型，包括那些具有RAG的模型。特别是，二元评分系统本身仍然会在搜索未能给出自信答案时奖励猜测。此外，搜索可能对字母计数示例中的计算错误或其他内在幻觉没有帮助。

潜在上下文。有些错误不能仅凭提示和响应来判断。例如，假设用户询问有关手机的问题，而语言模型提供的响应是关于手机的，但问题本意是关于座机的。这种歧义不符合我们的错误定义，因为它不依赖于提示和响应之外的上下文。将模型扩展到允许“隐藏上下文”（不包含在给语言模型的提示中，但可用于判断错误）将很有趣，这与偶然不确定性有关。

错误的三分法。我们的形式化没有区分不同大小或不确定程度的错误。显然，正确/错误/IDK类别也是不完整的。虽然统计理想可能是根据我们希望在下游应用中对语言模型进行评分的方式来评分每个评估，但明确的置信度目标为主流评估提供了一个实用、客观的修改，一个错误的三分法至少比一个错误的二分法提供了IDK选项。

超越IDK。有许多方式可以表示不确定性，例如对冲、省略细节和提问。最终，语言模型可能会遵循置信度概念，例如语言校准（Mielke 等，2022；Damani 等，2025）。然而，语言的语用现象（Austin, 1962; Grice, 1975）是微妙的。例如，虽然在某些情况下，语言模型明确陈述概率置信度估计可能很有用（Lin 等，2022a），但这也可能导致不自然的表述，例如，“我有1/365的把握认为Kalai的生日是3月7日。” 本文的重点是关于所说内容的顶层决策的统计因素。

6 结论

本文从预训练的起源到后训练的持续存在，揭开了现代语言模型中幻觉的神秘面纱。在预训练中，我们表明生成性错误类似于监督学习中的误分类，这并不神秘，并且由于交叉熵损失的最小化而自然产生。

许多语言模型的缺点可以通过单一评估来捕捉。例如，过度使用开场白“当然”可以通过单一的“当然”评估来解决（Amodei 和 Fridman，2024），因为以“当然”开头的响应不会显著影响其他评估。相比之下，我们认为大多数主流评估奖励幻觉行为。对主流评估进行简单修改可以重新调整激励机制，奖励适当的不确定性表达，而不是惩罚它们。这可以消除抑制幻觉的障碍，并为未来在更细致的语言模型方面的工作打开大门，例如，具有更丰富的语用能力（Ma 等，2025）。

致谢

我们感谢 Alex Beutel, Tom Cunningham，Yann Dubois, Parikshit Gopalan, Johannes Heidecke, Zoe Hitzig, Saachi Jain, Manas Joglekar, Sanjay Kairam, Ehud Kalai, Amin Karbasi, Alan Luo，Anay Mehrotra, Eric Mitchell, Cameron Raymond, David G. Robinson, Mandip Shah, Joshua Vendrow, Grigoris Velegkas, Rose Wang, Zhigang Wang, Jason Wolfe，和 Jason Wei 的有益讨论。

参考文献

（参考文献列表已省略，因其内容庞大且主要为引用信息，不影响核心论点的理解。）