从线性回归到 Softmax 回归：深度学习入门核心知识全解析
在深度学习的世界里，回归模型是我们探索数据规律、解决实际问题的重要工具。无论是给心仪的房子估算价格，还是对海量图像进行分类，都离不开线性回归与 Softmax 回归的身影。本文将带大家深入剖析这两种经典回归模型，从基本原理到优化方法，再到实际应用，全方位解锁深度学习入门的关键知识点。
一、线性回归：预测连续值的 “价格估算师”
（一）生活中的线性回归：给房子定价
当我们看中一套房子，想要估算它的合理价格并出价时，线性回归就能派上用场。我们可以收集往年类似房子的交易数据，比如房子的面积、卧室数量、地理位置等特征，以及对应的成交价格（即Price）。像 A 房子付了多少、B 房子付了多少这样的往年房价数据，都是线性回归的宝贵训练素材。通过这些数据，线性回归模型能找到特征与价格之间的线性关系，从而为我们看中的房子给出合理的价格估算。
（二）线性回归的数学表达
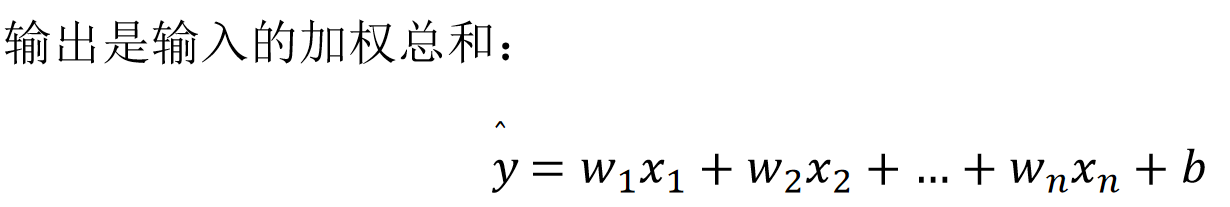
w称为权重，决定了每个特征对我们预测值的影响 b称为偏置
（三）从线性回归到神经网络的过渡
线性回归其实可以看作是最简单的神经网络结构。它包含一个输入层和一个输出层，输入层接收样本的特征（如房子的各项特征），输出层则输出预测的目标值（如房子的价格）。在这个简单的神经网络中，输入层的每个神经元（对应一个特征）与输出层的神经元之间都有一个连接权重（即w中的元素），输出层神经元还会加上偏置项b，最终得到预测结果。这种结构为我们理解更复杂的神经网络奠定了基础，复杂的神经网络就是在这样简单的结构上，通过增加隐藏层、增多神经元数量等方式构建起来的。
二、模型训练的核心：损失函数与优化算法
要让线性回归（以及后续的 Softmax 回归）模型发挥作用，就需要通过训练不断调整参数（权重w和偏置b），而这离不开损失函数和优化算法。
（一）损失函数：衡量模型预测的 “误差”
损失函数的作用是计算模型预测值与真实值之间的差异，它是我们调整参数的 “指南针”。常见的损失函数有以下几种：
- 平方损失（L2 损失）：其计算公式为
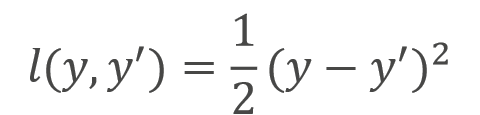，其中yi是真实值，y^i是预测值，n是样本数量。平方损失对较大的误差惩罚更严重，能让模型更关注偏差较大的样本。 - L1 损失：计算公式为
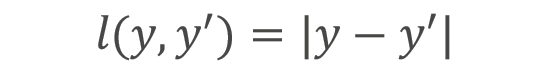。与平方损失相比，L1 损失对异常值的鲁棒性更强，因为它对误差的惩罚是线性的，不会过度放大异常值的影响。 - Huber 损失：结合了 L1 损失和 L2 损失的优点。当预测误差较小时，采用平方损失（让模型收敛更快）；当误差较大时，采用 L1 损失（减少异常值的影响）。其表达式为：
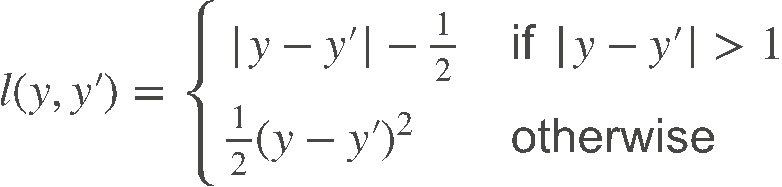其中δ是一个超参数，用于控制两种损失的切换阈值。 - 交叉熵损失：在分类问题中应用广泛（后续Softmax回归会详细介绍），主要用于衡量两个概率分布之间的差异。计算公式为
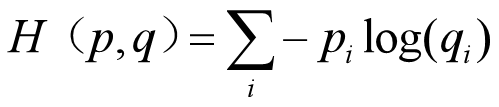，其中p是真实概率分布，q是模型预测的概率分布。
二）优化算法：寻找最优参数的“路径”
优化算法的目标是通过调整参数，使损失函数的值达到最小，从而找到模型的最优参数。
- 梯度法：梯度是由函数所有变量的偏导数汇总而成的向量。它指示的反方向是函数值减小最多的方向。在梯度法中，我们从当前参数位置出发，沿着梯度的反方向更新参数，然后在新的位置重新计算梯度，重复这个过程，直到损失函数的值收敛到最小值（或接近最小值）。
需要注意的是，梯度方向只是当前位置函数值减小最快的方向，不能保证一定能找到函数的全局最小值，也可能陷入局部最小值。但在实际应用中，梯度法依然是最常用的优化方法之一。 - 随机梯度下降（SGD）：传统的梯度下降需要使用全部训练数据计算梯度，计算量较大，训练速度慢。随机梯度下降则每次从训练数据中随机选择一个样本，用这个样本的梯度来更新参数。这种方式大大减少了计算量，加快了训练速度，但参数更新的波动较大，收敛过程不稳定。
- 小批量随机梯度下降（Mini-batch SGD）：结合了传统梯度下降和随机梯度下降的优点。它每次从训练数据中选择一小批样本（批量大小通常为32、64、128等），用这一批样本的平均梯度来更新参数。
梯度：使得函数值增加最快的方向，更新权重的方向
在选择批量大小时，需要注意以下两点：
批量值不能太小：如果批量值太小，每次计算的梯度随机性较大，难以充分利用计算机的并行计算资源，训练效率低。
批量值不能太大：如果批量值太大，虽然梯度估计更稳定，但会浪费计算资源（比如批量过大可能导致内存不足），而且训练过程中参数更新的频率降低，收敛速度变慢。
梯度下降通过不断的沿着反梯度方向更新参数求解
小批量随机梯度下降是深度学习默认的求解算法
（三）超参数选择：影响模型训练的“关键开关”
在模型训练过程中，除了模型的参数（权重和偏置），还有一些需要人工设置的参数，称为超参数。其中，学习率和批量大小是两个最重要的超参数
- 学习率：控制每次参数更新的幅度。学习率不要太大：如果学习率过大，参数更新的幅度会很大，可能会导致损失函数的值在最小值附近震荡，甚至无法收敛。学习率不要太小：如果学习率过小，参数更新的幅度很小，训练过程会非常缓慢，需要大量的迭代次数才能收敛到最小值。在实际应用中，通常会采用学习率调度策略，比如随着训练轮次的增加，逐渐减小学习率，让模型在训练初期快速收敛，在后期精细调整参数。
- 批量大小：如前所述，批量大小需要根据计算资源和训练效率进行合理选择，找到一个既能充分利用资源，又能保证训练稳定性和收敛速度的平衡点。
学习率：步长的超参数，每次沿梯度方向一步走多远
三、Softmax回归：解决多分类问题的“利器”
线性回归主要用于预测连续值，而在实际应用中，我们经常会遇到分类问题（如手写数字识别、图像分类、文本情感分析等），Softmax回归就是专门用于解决多分类问题的模型。
（一）回归与分类的区别
回归 ：单个连续数值输出 自然区间 与真实值的区别作为损失
分类 ：通常多个输出 输出的i表示预测为第i类的置信度
（二）Softmax回归的网络结构
Softmax回归是一个单层神经网络，同时也是一个全连接层。它的输入层接收样本的特征，输出层的神经元数量等于类别的数量。
例如，在手写数字识别问题中，输入层接收手写数字图像的像素特征（如MNIST数据集的图像为28×28像素，输入特征数为784），输出层有10个神经元（对应0-9这10个数字类别）。每个输出神经元的输出值经过Softmax运算后，得到对应类别的概率。
由于每个输出神经元的计算都依赖于所有输入特征，因此Softmax回归层是全连接层。
（三）Softmax回归的损失函数：交叉熵损失
在Softmax回归中，常用交叉熵损失来衡量模型预测的概率分布与真实概率分布之间的差异。
假设训练样本的真实标签采用独热编码（即对于属于第i类的样本，其真实概率分布p中，pi=1，其他类别的概率为0），模型预测的概率分布为q，则交叉熵损失的计算公式为L=−∑i=1Kpilog(qi)=−log(qj)（其中j是样本的真实类别）。
交叉熵损失能够有效惩罚模型预测概率与真实标签偏差较大的情况，推动模型不断调整参数，提高对正确类别的预测概率。
（四）Softmax 运算：将置信度转化为概率
为了更好地处理多类分类任务，Softmax 回归引入了 Softmax 运算。Softmax 运算的作用是将模型输出的置信度转化为概率分布，满足概率的两个基本性质：（非负，和为1）
四、总结：深度学习入门的“核心要点”
- 线性回归是预测连续值的基础模型，其数学表达式为y=wTx+b（多变量），可看作最简单的神经网络。
- Softmax回归是解决多分类问题的重要模型，通过Softmax运算将模型输出转换为概率分布，结合交叉熵损失进行训练。
- 损失函数是衡量模型误差的标准，常见的有平方损失、L1损失、Huber损失、交叉熵损失等，需根据具体问题选择。
- 优化算法是寻找最优参数的关键，梯度法是基础，随机梯度下降和小批量随机梯度下降是常用的优化方法。
- 学习率和批量大小是重要的超参数，学习率控制参数更新幅度，批量大小影响训练效率和稳定性，需合理选择。
通过掌握线性回归和Softmax回归这两个基础模型，以及对应的损失函数和优化算法，我们就能为后续学习更复杂的神经网络（如卷积神经网络、循环神经网络等）打下坚实的基础。希望本文能帮助大家轻松入门深度学习，开启人工智能的学习之旅！