自动驾驶中的传感器技术50——Radar(11)
本节开始介绍雷达前端算法,即雷达如何配置。
首先这里推荐两本书:FMCW Radar Design 和 Radar Signal Processing for Autonomous Driving
1、FMCW测速
Triangular Chirp测速
Ref:https://wirelesspi.com/fmcw-radar-part-2-velocity-angle-and-radar-data-cube/
由于运动本身会产生多普勒频率 fd,因此拍频 fb 会偏移与 fd 相等的量。下图分别展示了正多普勒和负多普勒两种情况。
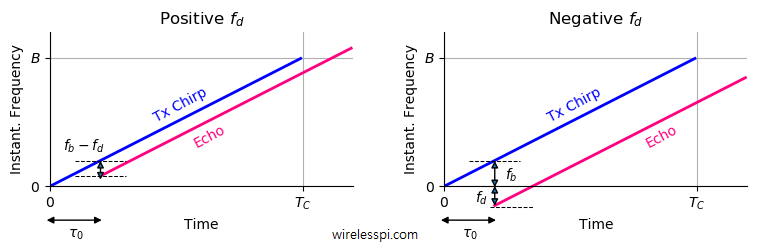
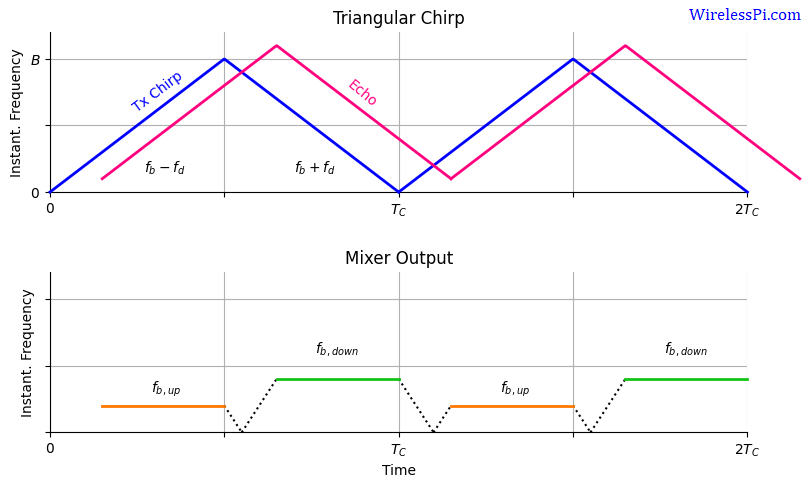
fb,up=fb−fd
fb,down=fb+fd
fb=μ*2d0/c=(fb,down+fb,up)/2
fd=2v/λ=(fb,down–fb,up)/2
d0=(fb,down+fb,up)*c/(4μ)
v=(fb,down–fb,up)*λ/4
以上方案的核心思想是采用两种不同的Chirp 速率+μ和-μ,因此它仅适用于单个运动目标的距离和速度。如果存在多个目标,则两个方程不足以确定它们的距离和速度。此外,例如,第一个目标和第二个目标的直线相交处会出现Ghost目标,这会导致距离-速度图出现模糊。
实际在FMCW雷达中的采用一个简单的解决方案,它基于这样一个事实:多普勒频率从一个Chirp到下一个Chirp的变化可以忽略不计。从下面显示的传统线性 FMCW 波形中提取距离和速度。
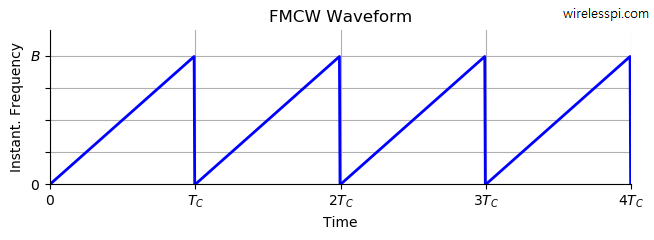
Chirp波形相位部分如下
ϕ=πμτ0(2)−2πfτ0=π(μτ0)τ0−2πfτ0
上式给出了τ0秒内相位的变化:第一项中相位变化来自拍频,第二项中相位变化来自载波频率。虽然τ0出现在上面的表达式中,但由于2π周期的限制,它无法用于测距。
虽然 FMCW 雷达的相位仍然限制在 2π 范围内,但一种巧妙的技术可以使其用于速度估计。
假设在时间 t=0 时,FMCW 雷达发出一个chirp,该chirp需要 τ0 秒才能到达目标并返回。混频器输出或中频信号的相位由上述表达式给出。我们将其称为 ϕ0。在另一个时刻,比如 t=TC(扫描时间),雷达发出另一个chirp,该chirp同样需要 τ0 秒才能到达目标。如果物体静止不动,则混频器之后接收到的相位(与 ϕ0 相比)没有变化,将其表示为 ϕ1。
Δϕ=ϕ1−ϕ0=0
现在想象一下,在两次chirp之间的时间间隔内,目标以速度 v 移动了很短的距离 Δd=vTC。
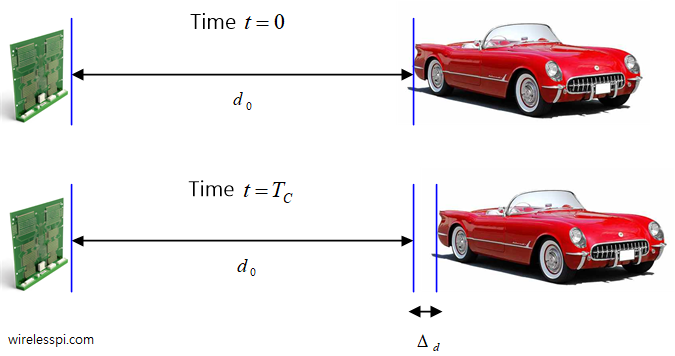
在这种情况下,相位如何变化?虽然在 t=0 时相位仍为 ϕ0,但当 t=nTC 时,相位会逐渐变化,如下图所示。例如,当 n=1 或时间 t=TC(扫描时间)时,chirp的传播时间为 τ0+Δτ 秒。
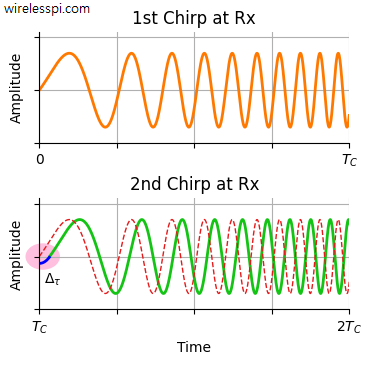
Δτ=2Δd/c=2vTC/c
ϕ1=−(2πμΔτ)t+πμΔτ(2)+2πμτ0Δτ−2πfΔτ+ϕ0
假设
-
Speed of EM wave c=3×10(8) m/s
-
Frequency f=77×10(9) Hz
-
Sweep time TC=40×10(−6) seconds
-
Chirp rate μ=40 MHz/microsecond =40×10(12) Hz/second
-
Range d0=20 m
-
Velocity v=36 km/hr =10 m/s
对于上式第一项可以计算得到
Change in phase=2πμΔτTC≈0.02radians
对于上式第二项可以计算得到
πμΔ2τ≈9×10(−10),可以忽略
对于上式第三项可以计算得到
2πμτ0Δτ≈4.5×10(−5),可以忽略
对于上式第四项可以计算得到
2πfΔτ=1.29,与 ϕ0 相比,这是导致 ϕ1 发生变化的唯一重要因素。
所以上式可以重写为
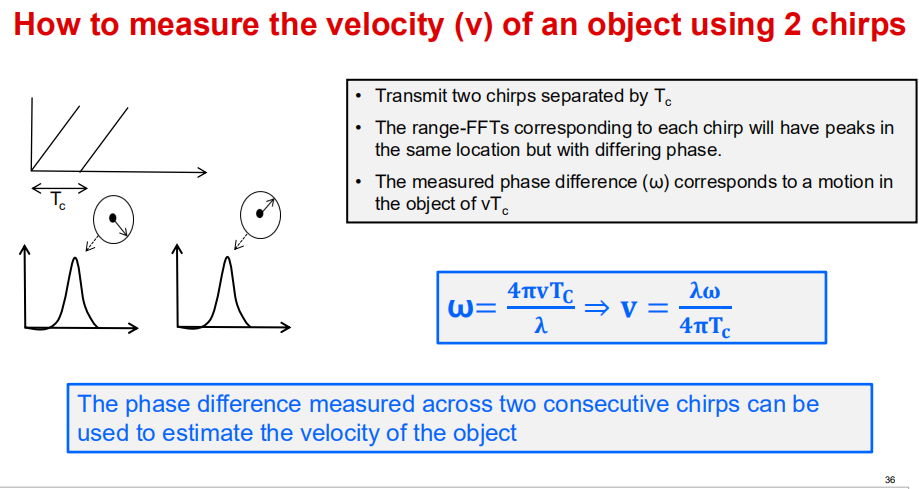
Δϕ=ϕ1−ϕ0≈−2πfΔτ=2πf2Δd/c=4πΔd/λ=2π2vTC/λ
得到速度如下
v=λ*Δϕ/(4π*TC)
我们原本以为我们关注的是相位,但实际上我们测量的是一定时间内相位的变化率,而这正是频率的定义!这本身就是多普勒频率。总而言之,单个目标的距离可以通过拍频找到,而单个目标的速度则隐藏在一段时间内的相位演变中,这与多普勒频率类似。
对于一段时间内的第 n 个 chirp,可以将其概括为
ϕn=ϕ0−2πf⋅nΔτ,n=0,1,⋯,N−1
对于典型速度,距离FFT中的距离单元(bin) k上的delta函数或sinc函数(表示拍频fb)在N次扫描周期内变化不大,可以视为常量(如下图所示)。该常量理想情况下位于δ[k−kb]。另一方面,在上述表达中,相位ϕn是变化的。
v[n]=constant⋅exp(jϕn)→exp(j2πf⋅nΔτ)=exp(j2πn*2vTC/λ)
上式是一个“频率”为 2vTC/λ 的复正弦波。下图对此进行了说明,其中沿多普勒维度的相位演变与 FFT 幅度一起绘制。显然,距离单元中的相位会生成另一个复正弦波(其中 sin(⋅) 部分也显示出来),可用于速度估计。
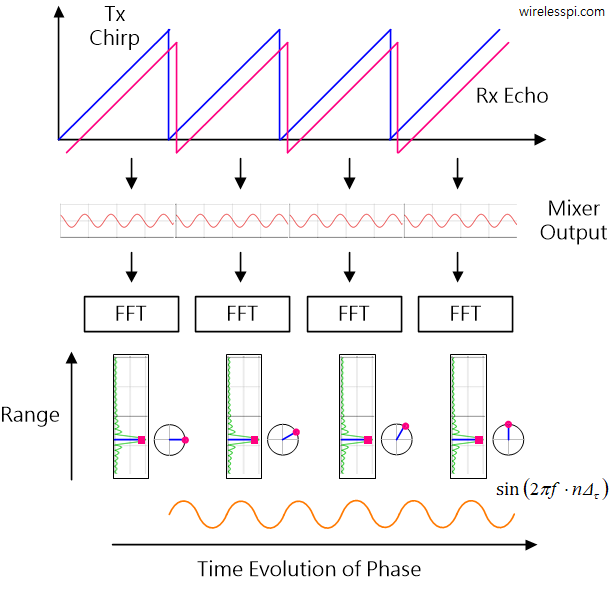
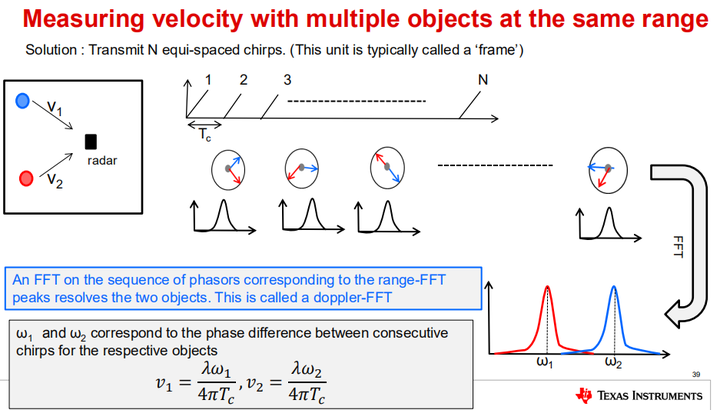
存在多个目标时的输出变为
v[n]=constant1⋅exp(j2πn*2v1TC/λ)+constant2⋅exp(j2πn*2v2TC/λ)+constant3⋅exp(j2πn*2v3TC/λ)
沿此 n 轴进行另一次傅里叶变换(即在距离 FFT 的频率区间上逐个chirp地进行),会发现一个峰值,该峰值对应于 2vTC/λ,从而对应于每个目标的速度。此二维 FFT 输出称为距离-多普勒图 (RDM)。
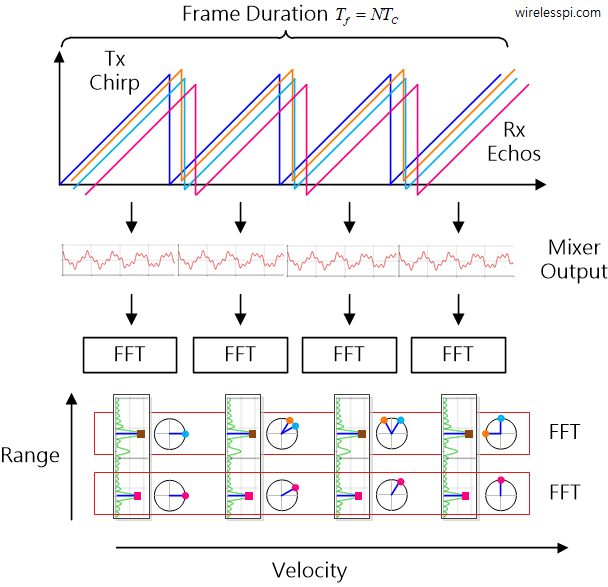
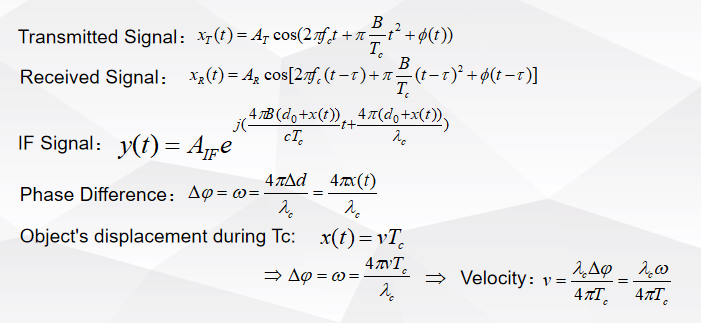
2、测速Chirp配置
了解了FMCW的测试算法,就需要依据该算法对雷达的Frame-Chirp进行配置。
Ref:https://www.ti.com/lit/an/swra553a/swra553a.pdf?ts=1758031246994
最大测量速度
快速 FMCW 调制雷达的最大可测速度取决于线性调频脉冲周期,即两个连续线性调频脉冲起始时间之间的时间差。这又取决于频率扫描的速度以及允许的最小线性调频脉冲间隔时间。
MMIC 的频率上升速度越快,最大无模糊速度就越高。例如100 MHz/µs 的快速上升速率。此外,闭环 PLL 的设计也支持频率上升的快速稳定。因此,VCO 从上升频率末端跳变到重新开始下一个上升频率所需的时间非常短,从而允许更短的空闲时间(低至 2 µs)。
Unambiguousmax velocity = λ/(4TC)
TC → 总线性调频脉冲时间,包括线性调频脉冲时间 + 空闲时间
λ → 所用信号的波长
使用更高级的算法,可以将实际可测最大速度扩展到无模糊最大速度之外。
速度测量分辨率
速度分辨率主要取决于传输帧的持续时间,也就是说,增加帧中的线性调频脉冲数量可以提高速度分辨率。
Unambiguousmax velocity = λ/(2NTC)
Nc → 帧中的线性调频脉冲数量

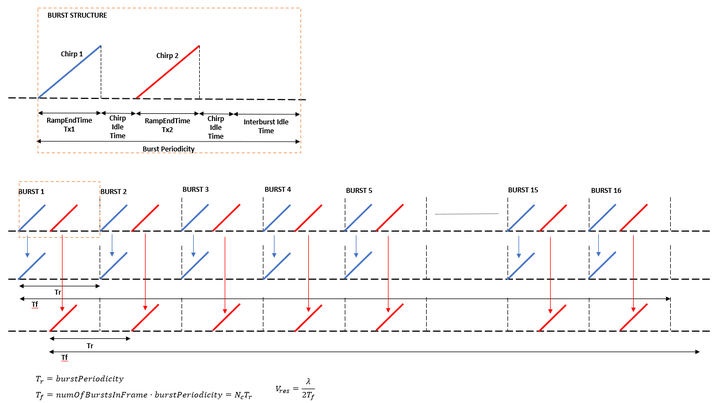
多普勒分析是针对每个天线进行的。考虑到这一点,为了简单起见,假设只有一个接收天线(但该分析可以推广到所有天线对),我们可以将chirp分成两个序列,每个序列包含 16 个样本:一个由第一个发射天线发射的 16 个chirp组成(蓝色chirp),另一个由第二个发射天线发射的 16 个chirp组成(红色chirp)。
两个序列有相同之处:
-
最大速度:Vmax = c / (4 * fc * Tr) = 3e8/(4 * 60.26e9 * 800e-6) = 1.555 m/s
-
速度分辨率:Vres = c / (2 * fc * Tf ) = c / (2 * fc * Nc * Tr ) = 3e8/(2 * 60.26e9 * 16 * 800e-6) = 0.1944 m/s。或者,Vres = 2 * Vmax / Nc = 2 * 1.555 / 16 = 0.1944 m/s。
3、RD处理流
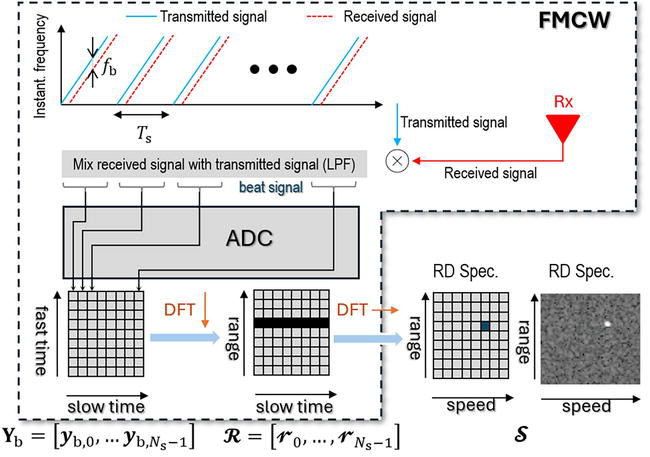
Ref:https://www.intechopen.com/chapters/1217095
