当前位置：首页 > news >正文

构建AI智能体：三十六、决策树的核心机制（二）：抽丝剥茧简化专业术语推理最佳分裂点

news 2025/9/18 10:12:04

一、决策树回顾

在大家读这篇文章前，如果对决策树还没有什么概念，可以先看看前一篇《构建AI智能体：三十五、决策树的核心机制（一）：刨根问底鸢尾花分类中的参数推理计算》，先简单回顾一下决策树：通过提出一系列问题，对数据进行层层筛选，最终得到一个结论（分类或预测），每一个问题都是关于某个特征的判断，而每个答案都会引导我们走向下一个问题，直到得到最终答案。

昨天我们通过鸢尾花数据集构建的决策树，初步了解了基尼不纯度值、样本等一些基础概念，今天将继续刨根问底，进一步探索一些核心的标准值，了解最佳分裂阈值、信息增益以及加权基尼不纯度等核心值的计算方式和对整体决策的影响。

首先看看鸢尾花的决策流程，今天我们用一个流程图来代替。

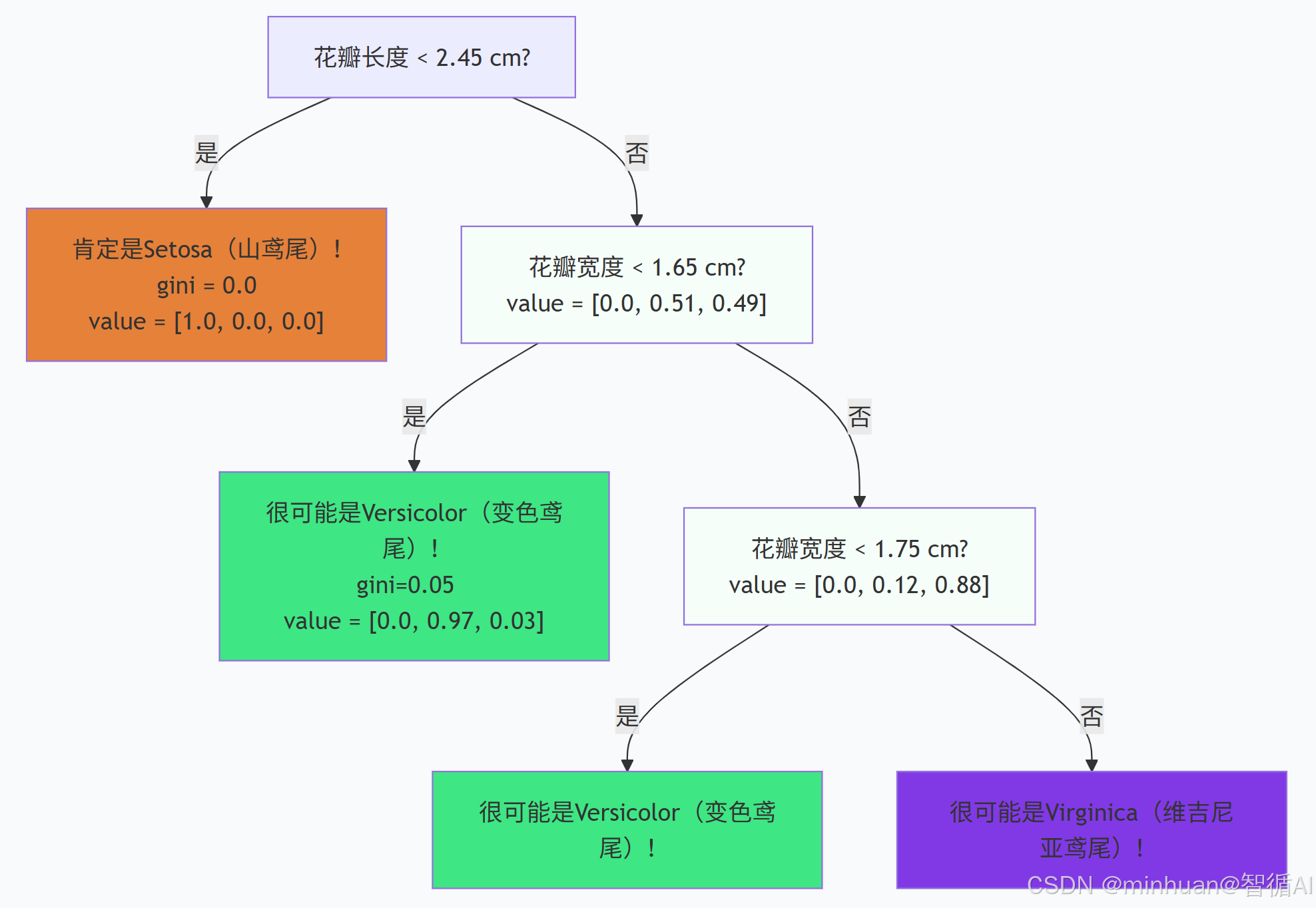
1. 模型的决策逻辑

第一问：花瓣长度 <= 2.45？

是 -> 左分支：
- 我们看到了一个gini = 0.0的叶节点。这是一个100%纯净的节点！
- value = [1.0, 0.0, 0.0] 意味着所有走到这里的样本，100%都是山鸢尾（Setosa）。
- 结论：模型发现了一个黄金定律——只要花瓣长度小于等于2.45厘米，就一定是山鸢尾。这个规则在训练数据中毫无例外。
否 -> 右分支：
- 既然不是山鸢尾，那就只可能是变色鸢尾或维吉尼亚鸢尾了。模型需要继续提问。
- 这个节点显示 value = [0.0, 0.51, 0.49]，证实了这一点（山鸢尾为0，另外两类几乎各占一半）。

第二问（对非Setosa的花）：花瓣宽度 <= 1.65？

是 -> 左分支：
- 这里又有一个非常纯净的节点（gini=0.05）。value = [0.0, 0.97, 0.03] 表示97%是变色鸢尾。
- 结论：如果花瓣宽度 <= 1.65 cm，那么这朵花极大概率是变色鸢尾。
否 -> 右分支：
- 这里的情况稍微复杂一点，需要再问一个问题。

第三问（对上述右分支的花）：花瓣宽度 <= 1.75？

这是一个更细粒度的区分，最终将剩下的花也成功地分离成了主要是变色鸢尾或主要是维吉尼亚鸢尾的组。

由此可见：

如果有一朵花，其花瓣长度 > 2.45 cm 且花瓣宽度 <= 1.65 cm，模型会非常自信地将其分类为变色鸢尾。
如果另一朵花，其花瓣长度 > 2.45 cm，花瓣宽度 > 1.65 cm，且花瓣宽度 > 1.75 cm，模型会非常自信地将其分类为维吉尼亚鸢尾。
如果一朵花不在以上的明确区间，只在少数节点（如gini=0.5）表现出不确定性，那里两类花各占一半，需要更多信息和条件去进行深度决策。

2. 模型的决策总结

黄金法则：如果花瓣长度 ≤ 2.45 cm，那它100%是山鸢尾 (Setosa)。这是最清晰、最绝对的规律。
主要规律：对于花瓣长度 > 2.45 cm的花：
- 如果花瓣宽度 ≤ 1.65 cm，它极大概率是变色鸢尾 (Versicolor)。
- 如果花瓣宽度 > 1.75 cm，它极大概率是维吉尼亚鸢尾 (Virginica)。
模糊地带：在花瓣宽度在 1.65 cm 到 1.75 cm 这个非常窄的区间里，模型会比较困惑，因为两种花的数据在这个区间有重叠。

这棵决策树不仅仅是一个模型，更是一个数据报告，它清晰地揭示了这三种花在物理特征上的差异和边界。

二、决策树最佳分裂点探索

1. 什么是决策树的最佳分裂点

决策树的最佳分裂点是指在构建决策树时，算法选择的那个能够最有效区分不同类别的特征值阈值。这个点是决策树算法的核心，它决定了树的结构和预测性能。

在我们做鸢尾花的分类决策时，不知道大家有没有注意到其中的几个固定值，像2.45、1.65这些，特别是1.65，我们今天围绕的核心就是找到决策树中的这个1.65是如何产生的。

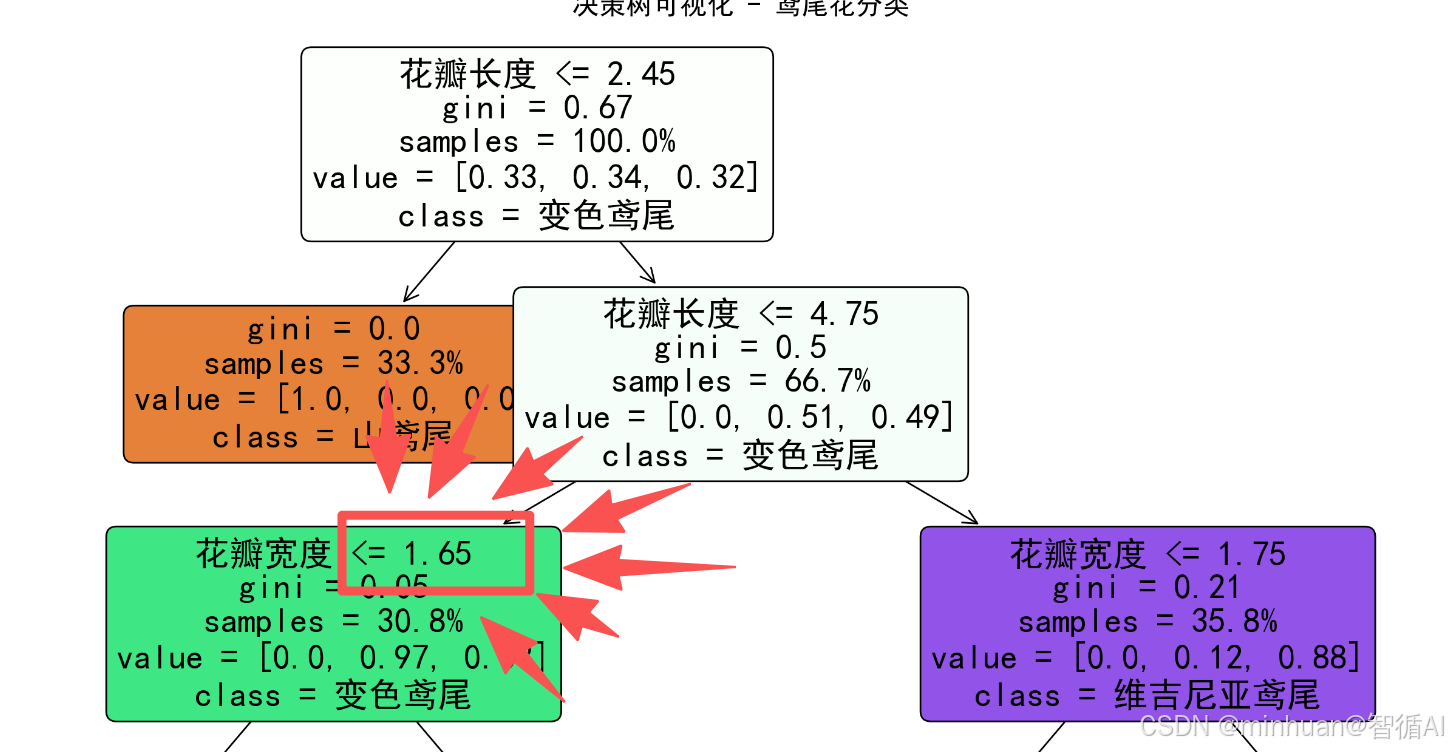
2. 最佳分裂点的核心原理

决策树通过最小化不纯度来找到最佳分类点。具体来说：

不纯度衡量：使用基尼不纯度或信息熵来衡量节点的"混乱程度"
分裂评估：对每个可能的分裂点，计算分裂后子节点的加权不纯度
最优选择：选择能使加权不纯度最小的分裂点作为最佳分类点

抛开繁杂的概念术语，重点讲一些息息相关的概念，通过最直接的示例输出来理解深层的含义。

2.1 关键概念：纯度与不纯度

纯度：指的是一个节点中样本属于同一类别的程度。纯度越高，节点中的样本越相似。
纯度衡量标准：
- 基尼不纯度：衡量随机抽取两个样本，它们属于不同类别的概率
- 信息增益：基于信息熵，衡量不确定性减少的程度

下面我们直接看看基尼不纯度的示例：

import numpy as np
def gini_impurity(labels):"""计算基尼不纯度：值越低表示越纯净"""if len(labels) == 0:return 0# 计算每个类别的比例proportions = np.bincount(labels) / len(labels)# 基尼不纯度 = 1 - Σ(比例²)return 1 - np.sum(proportions ** 2)# 示例：
print(gini_impurity([0, 0, 0, 0, 0]))     # 输出：0.0 （完全纯净）
print(gini_impurity([1, 1, 1, 1, 1]))     # 输出：0.0 （完全纯净）
print(gini_impurity([0, 0, 0, 1, 1]))     # 输出：0.48 （不太纯净）
print(gini_impurity([0, 1, 2, 3, 4]))     # 输出：0.7999999 （非常不纯净）

第一个数组[0, 0, 0, 0, 0] 输出的结果是0.0，说明完全纯净
第二个数组[1, 1, 1, 1, 1] 输出的结果是0.0，说明完全纯净
第三个数组[0, 0, 0, 1, 1] 输出的结果是0.48，说明不太纯净
第四个数组[0, 1, 2, 3, 4] 输出的结果是0.7999999，说明非常不纯净
由此可见，基尼不纯度理解也比较简单，范围为0到1，0表示完全纯净，1表示最大不纯度

2.2 重要：加权平均基尼不纯度

提示：这里对后面很重要，稍微有点晦涩难懂，可以拿个纸笔简单的画画计算一下

2.2.1 核心概念

决策树分裂的成本效益分析，是决策树用来评估一个分裂点好坏的价格标签。它综合考虑了分裂后两个子节点的纯净程度和每个子节点的规模，最终给出一个总体评分。这个值越低，说明分裂效果越好。

2.2.2 简单的比喻

想象你是一位老师，要把一个班级的学生按性别分成两组进行活动。你的目标是让每一组的性别纯度尽量高（要么全是男生，要么全是女生）。

方案A：你把40个学生分成 [20个男生] 和 [20个女生]。
- 左边组纯度：100%（全是男生）
- 右边组纯度：100%（全是女生）
方案B：你把40个学生分成 [2个男生] 和 [38个学生：18个男生 + 20个女生]。
- 左边组纯度：100%（全是男生）
- 右边组纯度：很差（男女混合）

加权平均基尼不纯度就是用来量化这种“整体效果”的指标。它不会只看一个组的纯度，而是会考虑每个组的人数权重，计算一个总的“不纯度得分”。

哪个方案更好？显然是方案A。虽然两个方案的左边组纯度都是100%，但方案A的右边组也非常纯净，而方案B的右边组几乎和原来一样混乱。

2.2.3 强化理解

2.2.3.1 基尼不纯度：衡量一个节点的混乱程度

首先，理解基尼不纯度。它衡量的是一个节点内部数据的“混乱程度”。

值域：0 到 0.5
0：完美纯净（节点内所有样本都属于同一类别）
接近0.5：极度混乱（节点内样本均匀分布在各个类别中）

计算公式：Gini = 1 - (p₁)² - (p₂)² （其中 p₁, p₂ 是两类样本的比例）

2.2.3.2 加权：“权重”为什么重要？

加权意味着我们不是简单地将两个子节点的不纯度相加，而是根据每个节点所含样本数量的比例来分配重要性。

一个节点样本数越多，它的不纯度对总体影响就越大。
这很合理：一个有1000个样本的节点变得纯净，比一个只有10个样本的节点变得纯净，意义要重大得多。

2.2.3.3 加权平均基尼不纯度：综合评分

现在，我们把前两个概念结合起来。

计算公式：

加权平均基尼不纯度 = (左节点样本数 / 总样本数) * 左节点基尼不纯度 + (右节点样本数 / 总样本数) * 右节点基尼不纯度

这个值代表了使用某个分裂点后，所产生的两个新节点的总体不纯度。

2.2.3.4 实例计算

让我们用鸢尾花数据来实际算一下，为什么“花瓣长度 ≤ 2.45cm”是一个好分裂点。
假设父节点有100个样本（50朵Versicolor + 50朵Virginica），其基尼不纯度很高。

我们测试分裂点 t = 2.45 cm。

分裂后：

左节点（花瓣长度 ≤ 2.45 cm）：假设有50个样本，全部是Versicolor。
基尼不纯度 = 1 - (50/50)² - (0/50)² = 0 （完全纯净）
右节点（花瓣长度 > 2.45 cm）：有50个样本，全部是Virginica。
基尼不纯度 = 1 - (0/50)² - (50/50)² = 0 （完全纯净）
计算加权平均基尼不纯度：= (50/100) * 0 + (50/100) * 0 = 0

结论： 加权平均基尼不纯度为 0，这是最佳可能结果！说明这个分裂点完美地将数据分成了两个纯净的节点。

相比我们测一个坏的分裂点，假设我们选择一个很差的分裂点 t = 4.0 cm。

分裂后：

左节点（≤ 4.0 cm）：有60个样本（50朵Versicolor + 10朵Virginica）
基尼不纯度 = 1 - (50/60)² - (10/60)² ≈ 0.277
右节点（> 4.0 cm）：有40个样本（0朵Versicolor + 40朵Virginica）
基尼不纯度 = 0 （纯净）
计算加权平均基尼不纯度：= (60/100) * 0.277 + (40/100) * 0 ≈ 0.166

结论： 加权平均基尼不纯度为 0.166，远高于0。说明这个分裂效果不好，因为左节点仍然非常混乱。

决策树算法会尝试所有可能的分裂点，最终选择那个能使加权平均基尼不纯度最小化的点（在这个例子中，就是 t = 2.45 cm）

2.3 重要：不纯度减少量

提示：需求清楚基础概念，后面遇到不清楚可以回过来冥想一下

2.3.1 核心概念

决策树分裂的收益报告，不纯度减少量衡量的是提出一个问题所带来的价值。它告诉我们，通过某个分裂点将数据分成两组后，整体的混乱程度降低了多少。这个值越大，说明问的这个问题的价值越高。

也称信息增益：

分裂前：面对一堆混合的花，你很不确定它们的种类，不确定性很高。
分裂后：通过一个问题，你获得了信息，不确定性降低了。
信息增益：就是你通过这次分裂获得的信息量。获得的信息越多，这次分裂就越有价值。

2.3.2 简单的比喻

想象你的房间非常乱，标识高不纯度，里面堆满了衣服、书、零食和电子产品。你想通过整理来让房间变整洁，是为了降低不纯度。

整理方案A：你买了一个脏衣篓，把所有衣服都扔进去。现在房间看起来好多了，混乱程度大幅降低。
整理方案B：你把一支笔从桌上放回了笔筒。房间的混乱程度只有轻微降低。

不纯度减少量就是用来量化这种“混乱程度降低幅度”的指标。方案A的“不纯度减少量”远大于方案B，所以方案A是更值得做的高价值操作。

在决策树中，每个可能的分裂点就是一个“整理方案”，算法会选择那个能带来最大不纯度减少量的方案。

2.3.3 计算步骤

计算过程，遵循一个直观的公式：

不纯度减少量 = 分裂前的不纯度 - 分裂后的加权平均不纯度

第一步：计算分裂前的“混乱程度”（父节点不纯度）

首先，需要知道在没做任何事之前，当前节点的混乱程度有多高。我们用基尼不纯度来度量它。
示例：一个节点里有10个样本，5个是A类，5个是B类。
父节点不纯度 = 1 - (5/10)² - (5/10)² = 1 - 0.25 - 0.25 = 0.5

第二步：计算分裂后的“剩余混乱程度”（子节点加权不纯度）

然后，评估如果采用某个分裂规则（例如“特征X ≤ 阈值t”），将数据分成左右两个子节点后，整体的混乱程度还剩多少。这个值就是加权平均基尼不纯度。

示例：假设按某个规则分裂后：
左节点有6个样本，全是A类 -> 不纯度 = 0
右节点有4个样本，全是B类 -> 不纯度 = 0
加权平均不纯度 = (6/10)*0 + (4/10)*0 = 0

第三步：计算“混乱程度的降低量”（不纯度减少量）

最后，用第一步的值减去第二步的值，得到的就是这次分裂带来的收益。
不纯度减少量 = 0.5 - 0 = 0.5

结论：这个分裂点带来了0.5的不纯度减少量，这是一个巨大的收益，因为它完全消除了不纯度。

2.3.4 实例计算

让我们用鸢尾花数据的真实场景来计算一下，为什么“花瓣长度 ≤ 2.45cm”这个分裂点如此优秀。
场景：根节点有120个样本（假设训练集），其中40朵Setosa，40朵Versicolor，40朵Virginica。

计算分裂前的不纯度（父节点）：

Gini_parent = 1 - (40/120)² - (40/120)² - (40/120)² = 1 - (0.111) - (0.111) - (0.111) ≈ 0.667

计算分裂后的不纯度（使用花瓣长度 ≤ 2.45cm）：

左子节点（≤ 2.45cm）：假设有40个样本，全部是Setosa。
- Gini_left = 1 - (40/40)² - (0/40)² - (0/40)² = 0
右子节点（> 2.45cm）：有80个样本，40朵Versicolor，40朵Virginica。
- Gini_right = 1 - (0/80)² - (40/80)² - (40/80)² = 1 - 0 - 0.25 - 0.25 = 0.5
加权平均不纯度：
- Weighted_Gini = (40/120)*0 + (80/120)*0.5 ≈ 0 + 0.333 = 0.333

计算不纯度减少量（信息增益）：

Information Gain = Gini_parent - Weighted_Gini = 0.667 - 0.333 = 0.334

这个分裂点带来了0.334的不纯度减少量。这意味着它解决了父节点中近一半的混乱问题，是一个收益非常高的分裂决策。

如果另一个分裂点只能将加权不纯度从0.667降到0.600，那么它的不纯度减少量只有:Information Gain = 0.667 - 0.600 = 0.067,这个收益要小得多，因此算法不会选择它。

2.4 纯度和最佳分裂点的关系

纯度是决策树构建的根本目标和优化方向，决策树的一切行为都是为了最大化节点纯度，从而减少预测的不确定性。
最佳分裂点是算法为了实现纯度最大化这个目标，在经过穷举搜索和数学计算后，所选择的必然手段和最优路径。

2.5 了解 numpy.bincount函数

numpy.bincount 函数用于统计非负整数数组中每个元素的出现次数，简单来说，就是数数，给定一个数组，它会统计出这个数组中从 0 到最大值（max）之间，每一个整数出现的次数。

工作原理：

它先找到输入数组中的最大值 max_value。
然后创建一个长度为 max_value + 1 的新数组（因为我们从0开始计数）。
最后，它遍历输入数组，遇到数字 n，就在新数组的第 n 个位置（即索引为 n 的位置）上加 1。

import numpy as np
x = np.array([1, 1, 2, 2, 2, 3, 7, 8, 8, 10])
result = np.bincount(x)
print(result)
y = np.array([1, 1, 1, 1 ,1, 1])
result1 = np.bincount(y)
print(result1)
# 索引：  0 1 2 3 4 5 6 7 8 9 10
# 输出： [0 2 3 1 0 0 0 1 2 0 1]
# 输出： [0 6]

比较两个输出结果可知，输出数据的长度取决于数组中的最大值
数组1中有两个1，输出的结果在1的索引位值为2
数组2中有六个1，输出的结果在1的索引位值为6，依次类推

3. 最佳分裂点的探索流程

3.1 流程图

决策树使用穷举搜索结合不纯度最小化的原则来找到最佳分裂点。具体流程如下：

3.2 分步探索

为了简单直观更易于理解，示例中我们只采用两个样本，Versicolor（变色鸢尾花）和Virginica（维吉尼亚鸢尾花）两类花，并只使用花瓣宽度特征来推算最佳分类点；

3.2.1 固定随机抽样的状态

# 设置随机种子确保结果可重现
np.random.seed(42)

random_state 参数的作用，代码中的 random_state=42。这个参数控制了随机抽样的“种子”。

如果设置 random_state：每次运行代码，划分结果都是一样的。因此 value 的值也是固定的。42 只是一个常用例子，可以用任何数字。
如果不设置 random_state：每次运行代码，都会进行一次新的随机划分。因此每次看到的 value 值都可能略有不同。
所以，value 的值是“固定”还是“变化”，完全取决于我们的代码配置。

3.2.2 数据准备

加载鸢尾花数据集，只保留Versicolor和Virginica两类花，并只使用花瓣宽度特征

# 1. 加载鸢尾花数据集
iris = load_iris()
X, y = iris.data, iris.target
feature_names = iris.feature_names# 创建DataFrame以便更好地处理数据
df = pd.DataFrame(X, columns=feature_names)
df['target'] = y
df['species'] = [iris.target_names[t] for t in y]# 2. 只保留Versicolor和Virginica两类花，并只使用花瓣宽度特征
df_subset = df[df['target'] >= 1]  # 只取target=1和2的样本
X_subset = df_subset[['petal width (cm)']].values.flatten()
y_subset = df_subset['target'].valuesprint("步骤1: 数据准备")
print(f"数据集大小: {len(X_subset)}")
print(f"Versicolor (类别1)样本数: {sum(y_subset == 1)}")
print(f"Virginica (类别2)样本数: {sum(y_subset == 2)}")
print()

输出结果：

步骤1: 数据准备
数据集大小: 100
Versicolor (类别1)样本数: 50
Virginica (类别2)样本数: 50

3.2.3 对特征值进行排序

共计100个样本，份数于两种类型，按花瓣宽度从小到大进行排序

# 3. 对花瓣宽度值进行排序
sorted_indices = np.argsort(X_subset)
X_sorted = X_subset[sorted_indices]
y_sorted = y_subset[sorted_indices]print("步骤2: 样本排序后的花瓣宽度值和对应类别")
# for i in range(10):  # 只显示前10个
for i in range(len(X_sorted)):  # 只显示前10个print(f"花瓣宽度: {X_sorted[i]:.2f} cm, 类别: {y_sorted[i]}")
print("...")
print()

输出结果：

步骤2: 样本排序后的花瓣宽度值和对应类别
花瓣宽度: 1.00 cm, 类别: 1
花瓣宽度: 1.00 cm, 类别: 1
花瓣宽度: 1.00 cm, 类别: 1
花瓣宽度: 1.00 cm, 类别: 1
花瓣宽度: 1.00 cm, 类别: 1
花瓣宽度: 1.00 cm, 类别: 1
花瓣宽度: 1.00 cm, 类别: 1
花瓣宽度: 1.10 cm, 类别: 1
花瓣宽度: 1.10 cm, 类别: 1
花瓣宽度: 1.10 cm, 类别: 1
... (此步只输出10个，后续详细的输出)

3.2.4 生成的候选分裂阈值

候选分裂阈值是决策树算法在为连续特征（如花瓣宽度）寻找最佳分裂点时，所尝试的所有可能的分界值，并在分界点的中间划线，此值即为分裂阈值，此示例中我们需要找到类别发生变化的节点。例如1.0cm和1.1cm，此处的分裂阈值为（1.0+1.1)/2 = 1.05，依次类推

# 4. 生成候选分裂阈值（相邻值的中点）
candidate_thresholds = []
for i in range(len(X_sorted) - 1):if y_sorted[i] != y_sorted[i + 1]:  # 只在类别变化处考虑候选阈值threshold = (X_sorted[i] + X_sorted[i + 1]) / 2.0candidate_thresholds.append(threshold)print("步骤3: 生成的候选分裂阈值（在类别变化处）")
print(f"候选阈值数量: {len(candidate_thresholds)}")
print(f"前5个候选阈值: {candidate_thresholds[:5]}")
print(f"所有候选阈值: {candidate_thresholds}")
print()

输出结果：

步骤3: 生成的候选分裂阈值（在类别变化处）
候选阈值数量: 11
前5个候选阈值: [1.35, 1.4, 1.45, 1.5, 1.6]
所有候选阈值: [1.35, 1.4, 1.45, 1.5, 1.6, 1.6, 1.65, 1.7, 1.75, 1.8, 1.8]

完整的取值过程，在以下100个样本中，只要是连续的类别发生改变即产生分裂的阈值：
花瓣宽度: 1.00 cm, 类别: 1
花瓣宽度: 1.00 cm, 类别: 1
花瓣宽度: 1.00 cm, 类别: 1
花瓣宽度: 1.00 cm, 类别: 1
花瓣宽度: 1.00 cm, 类别: 1
花瓣宽度: 1.00 cm, 类别: 1
花瓣宽度: 1.00 cm, 类别: 1
花瓣宽度: 1.10 cm, 类别: 1
花瓣宽度: 1.10 cm, 类别: 1
花瓣宽度: 1.10 cm, 类别: 1
花瓣宽度: 1.20 cm, 类别: 1
花瓣宽度: 1.20 cm, 类别: 1
花瓣宽度: 1.20 cm, 类别: 1
花瓣宽度: 1.20 cm, 类别: 1
花瓣宽度: 1.20 cm, 类别: 1
花瓣宽度: 1.30 cm, 类别: 1
花瓣宽度: 1.30 cm, 类别: 1
花瓣宽度: 1.30 cm, 类别: 1
花瓣宽度: 1.30 cm, 类别: 1
花瓣宽度: 1.30 cm, 类别: 1
花瓣宽度: 1.30 cm, 类别: 1
花瓣宽度: 1.30 cm, 类别: 1
花瓣宽度: 1.30 cm, 类别: 1
花瓣宽度: 1.30 cm, 类别: 1
花瓣宽度: 1.30 cm, 类别: 1
花瓣宽度: 1.30 cm, 类别: 1
花瓣宽度: 1.30 cm, 类别: 1
花瓣宽度: 1.30 cm, 类别: 1    1.35
花瓣宽度: 1.40 cm, 类别: 2 1.4
花瓣宽度: 1.40 cm, 类别: 1
花瓣宽度: 1.40 cm, 类别: 1
花瓣宽度: 1.40 cm, 类别: 1
花瓣宽度: 1.40 cm, 类别: 1
花瓣宽度: 1.40 cm, 类别: 1
花瓣宽度: 1.40 cm, 类别: 1
花瓣宽度: 1.40 cm, 类别: 1   1.45
花瓣宽度: 1.50 cm, 类别: 2
花瓣宽度: 1.50 cm, 类别: 2 1.5
花瓣宽度: 1.50 cm, 类别: 1
花瓣宽度: 1.50 cm, 类别: 1
花瓣宽度: 1.50 cm, 类别: 1
花瓣宽度: 1.50 cm, 类别: 1
花瓣宽度: 1.50 cm, 类别: 1
花瓣宽度: 1.50 cm, 类别: 1
花瓣宽度: 1.50 cm, 类别: 1
花瓣宽度: 1.50 cm, 类别: 1
花瓣宽度: 1.50 cm, 类别: 1
花瓣宽度: 1.50 cm, 类别: 1
花瓣宽度: 1.60 cm, 类别: 1   1.6
花瓣宽度: 1.60 cm, 类别: 2   1.6
花瓣宽度: 1.60 cm, 类别: 1
花瓣宽度: 1.60 cm, 类别: 1   1.65
花瓣宽度: 1.70 cm, 类别: 2   1.7
花瓣宽度: 1.70 cm, 类别: 1   1.75
花瓣宽度: 1.80 cm, 类别: 2
花瓣宽度: 1.80 cm, 类别: 2
花瓣宽度: 1.80 cm, 类别: 2
花瓣宽度: 1.80 cm, 类别: 2
花瓣宽度: 1.80 cm, 类别: 2
花瓣宽度: 1.80 cm, 类别: 2
花瓣宽度: 1.80 cm, 类别: 2
花瓣宽度: 1.80 cm, 类别: 2   1.8
花瓣宽度: 1.80 cm, 类别: 1   1.8
花瓣宽度: 1.80 cm, 类别: 2
花瓣宽度: 1.80 cm, 类别: 2
花瓣宽度: 1.80 cm, 类别: 2
花瓣宽度: 1.90 cm, 类别: 2
花瓣宽度: 1.90 cm, 类别: 2
花瓣宽度: 1.90 cm, 类别: 2
花瓣宽度: 1.90 cm, 类别: 2
花瓣宽度: 1.90 cm, 类别: 2
花瓣宽度: 2.00 cm, 类别: 2
花瓣宽度: 2.00 cm, 类别: 2
花瓣宽度: 2.00 cm, 类别: 2
花瓣宽度: 2.00 cm, 类别: 2
花瓣宽度: 2.00 cm, 类别: 2
花瓣宽度: 2.00 cm, 类别: 2
花瓣宽度: 2.10 cm, 类别: 2
花瓣宽度: 2.10 cm, 类别: 2
花瓣宽度: 2.10 cm, 类别: 2
花瓣宽度: 2.10 cm, 类别: 2
花瓣宽度: 2.10 cm, 类别: 2
花瓣宽度: 2.10 cm, 类别: 2
花瓣宽度: 2.20 cm, 类别: 2
花瓣宽度: 2.20 cm, 类别: 2
花瓣宽度: 2.20 cm, 类别: 2
花瓣宽度: 2.30 cm, 类别: 2
花瓣宽度: 2.30 cm, 类别: 2
花瓣宽度: 2.30 cm, 类别: 2
花瓣宽度: 2.30 cm, 类别: 2
花瓣宽度: 2.30 cm, 类别: 2
花瓣宽度: 2.30 cm, 类别: 2
花瓣宽度: 2.30 cm, 类别: 2
花瓣宽度: 2.30 cm, 类别: 2
花瓣宽度: 2.40 cm, 类别: 2
花瓣宽度: 2.40 cm, 类别: 2
花瓣宽度: 2.40 cm, 类别: 2
花瓣宽度: 2.50 cm, 类别: 2
花瓣宽度: 2.50 cm, 类别: 2
花瓣宽度: 2.50 cm, 类别: 2

对比一下和我们输出的阈值是否是一致的；

3.2.5 评估每个候选阈值

# 5. 计算基尼不纯度的函数
def gini_impurity(labels):"""计算基尼不纯度"""if len(labels) == 0:return 0# 计算每个类别的比例proportions = np.bincount(labels) / len(labels)print(f"bincount类别计数: {np.bincount(labels)}, len: {len(labels)}, 每个类别的占比: {proportions}")# print(f"proportions: {proportions}")# 计算基尼不纯度: 1 - Σ(p_i)^2return 1 - np.sum(proportions ** 2)# 6. 评估每个候选阈值
results = []print("步骤4: 评估每个候选阈值")
for threshold in candidate_thresholds:# 根据阈值分割数据left_indices = X_subset <= thresholdright_indices = X_subset > thresholdl_indices = X_subset <= thresholdr_indices = X_subset > thresholdleft_labels = y_subset[left_indices]right_labels = y_subset[right_indices]print('*'*25+f"当前阈值：{threshold}"+'*'*25)print(f"样本全集合: {X_subset}")print(f"样本的分类: {y_subset}")# print(f"l_indices: {l_indices}")xx = [1 if x == True else 0 for x in l_indices]yy = [1 if x == True else 0 for x in r_indices]xxx = re.sub(",", "", str(xx))yyy = re.sub(",", "", str(yy))print(f"样本<=阈值: {xxx}")print(f"样本> 阈值: {yyy}")print(f"左边的子集: {left_labels}")# 计算基尼不纯度gini_left = gini_impurity(left_labels)print(f"左子集的基尼不纯度值: {gini_left}")print(f"右边的子集: {right_labels}")gini_right = gini_impurity(right_labels)print(f"右子集的基尼不纯度值: {gini_right}")# 计算加权平均基尼不纯度n_left, n_right = len(left_labels), len(right_labels)n_total = n_left + n_rightweighted_gini = (n_left / n_total) * gini_left + (n_right / n_total) * gini_rightprint(f"加权平均基尼不纯度: {weighted_gini:.6f}, left: {(n_left / n_total) * gini_left}, right: {(n_right / n_total) * gini_right}")# 计算不纯度减少量gini_parent = gini_impurity(y_subset)impurity_reduction = gini_parent - weighted_giniprint(f"不纯度减少量（信息增益）值: {impurity_reduction:.6f}, gini_parent: {gini_parent}, weighted_gini: {weighted_gini}")print(f"threshold: {threshold:.2f}, gini_left: {gini_left:.6f}, gini_right: {gini_right:.6f}, weighted_gini: {weighted_gini:.6f}, impurity_reduction: {impurity_reduction:.6f}, n_left: {n_left}, n_right: {n_right}")results.append({'threshold': threshold,'gini_left': gini_left,'gini_right': gini_right,'weighted_gini': weighted_gini,'impurity_reduction': impurity_reduction,'n_left': n_left,'n_right': n_right})

输出结果：

步骤4: 评估每个候选阈值
*************************当前阈值：1.35*************************
样本全集合: [1.4 1.5 1.5 1.3 1.5 1.3 1.6 1. 1.3 1.4 1. 1.5 1. 1.4 1.3 1.4 1.5 1.
1.5 1.1 1.8 1.3 1.5 1.2 1.3 1.4 1.4 1.7 1.5 1. 1.1 1. 1.2 1.6 1.5 1.6
1.5 1.3 1.3 1.3 1.2 1.4 1.2 1. 1.3 1.2 1.3 1.3 1.1 1.3 2.5 1.9 2.1 1.8
2.2 2.1 1.7 1.8 1.8 2.5 2. 1.9 2.1 2. 2.4 2.3 1.8 2.2 2.3 1.5 2.3 2.
2. 1.8 2.1 1.8 1.8 1.8 2.1 1.6 1.9 2. 2.2 1.5 1.4 2.3 2.4 1.8 1.8 2.1
2.4 2.3 1.9 2.3 2.5 2.3 1.9 2. 2.3 1.8]
样本的分类: [1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2]
样本<=阈值: [0 0 0 1 0 1 0 1 1 0 1 0 1 0 1 0 0 1 0 1 0 1 0 1 1 0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1 0 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
样本> 阈值: [1 1 1 0 1 0 1 0 0 1 0 1 0 1 0 1 1 0 1 0 1 0 1 0 0 1 1 1 1 0 0 0 0 1 1 1 1 0 0 0 0 1 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1]
左边的子集: [1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1]
bincount类别计数: [ 0 28], len: 28, 每个类别的占比: [0. 1.]
左子集的基尼不纯度值: 0.0
右边的子集: [1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2]
bincount类别计数: [ 0 22 50], len: 72, 每个类别的占比: [0. 0.30555556 0.69444444]
右子集的基尼不纯度值: 0.4243827160493827
加权平均基尼不纯度: 0.305556, left: 0.0, right: 0.3055555555555555
bincount类别计数: [ 0 50 50], len: 100, 每个类别的占比: [0. 0.5 0.5]
不纯度减少量（信息增益）值: 0.194444, gini_parent: 0.5, weighted_gini: 0.3055555555555555
threshold: 1.35, gini_left: 0.000000, gini_right: 0.424383, weighted_gini: 0.305556, impurity_reduction: 0.194444, n_left: 28,
n_right: 72

通过计算得出：阈值1.35，加权平均基尼不纯度 0.305556，信息增益值 0.194444

左、右子集的切分方式：

当前判断的阈值为1.35，以1.35为界，<=1.35的放左边，>1.35的放右边，为了直观，我拉开数组的间距
注意：样本集合和样本分类是初始适合固定产生的，不会发生变化
样本集合: [1.4 1.5 1.5 1.3 1.5 1.3 1.6 1. 1.3 1.4 1. 1.5 1. 1.4 1.3 1.4 1.5 1.0 1.5 1.1 1.8 ...]
样本分类: [1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 ...]
<=阈值: [0 0 0 1 0 1 0 1 1 0 1 0 1 0 1 0 0 1 0 1 0 1 ...]
> 阈值: [1 1 1 0 1 0 1 0 0 1 0 1 0 1 0 1 1 0 1 0 1 0 ...]

以1.35为边界，<=1.35的放左边，标记红色，>1.35的放右边，标记绿色

取出”<=阈值“集合中样本类型构成了左侧子集：
左边子集: [1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1]
取出”> 阈值“集合中样本类型构成了右侧子集
右边子集: [1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2]

3.2.6 找到最佳分裂点

# 7. 找到最佳分裂点
best_result = min(results, key=lambda x: x['weighted_gini'])
best_threshold = best_result['threshold']print("步骤5: 找到最佳分裂点")
print(f"最佳分裂阈值: {best_threshold:.4f} cm")
print(f"加权基尼不纯度: {best_result['weighted_gini']:.6f}")
print(f"不纯度减少量: {best_result['impurity_reduction']:.6f}")
print(f"左节点样本数: {best_result['n_left']}")
print(f"右节点样本数: {best_result['n_right']}")
print()

输出结果：

步骤5: 找到最佳分裂点
最佳分裂阈值: 1.7000 cm
加权基尼不纯度: 0.110306
不纯度减少量: 0.389694
左节点样本数: 54
右节点样本数: 46

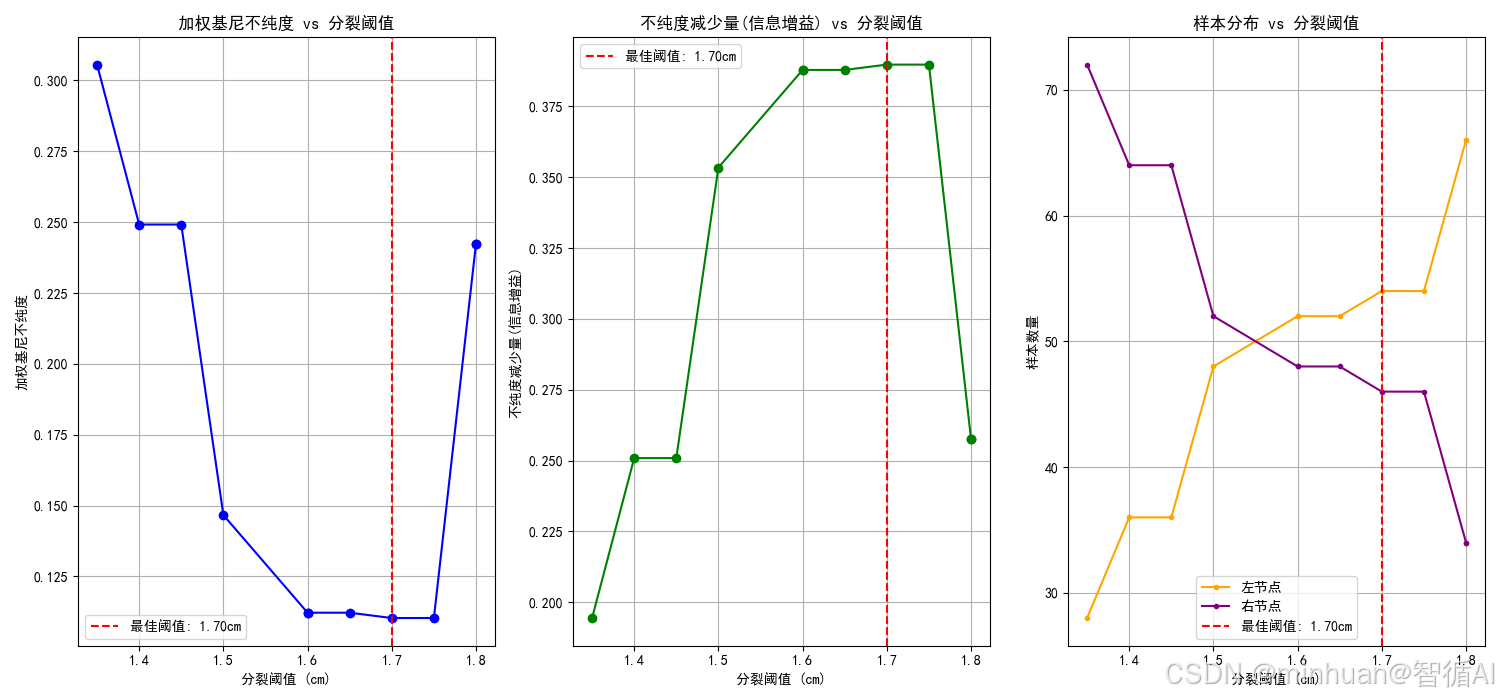
3.2.7 显示所有候选阈值的结果

# 8. 显示所有候选阈值的结果
print("步骤6: 所有候选阈值的结果比较")
results_df = pd.DataFrame(results)
print(results_df[['threshold', 'weighted_gini', 'impurity_reduction', 'n_left', 'n_right']].head(10))
print("...")
print()

输出结果：

步骤6: 所有候选阈值的结果比较
threshold weighted_gini impurity_reduction n_left n_right
0 1.35 0.305556 0.194444 28 72
1 1.40 0.249132 0.250868 36 64
2 1.45 0.249132 0.250868 36 64
3 1.50 0.146635 0.353365 48 52
4 1.60 0.112179 0.387821 52 48
5 1.60 0.112179 0.387821 52 48
6 1.65 0.112179 0.387821 52 48
7 1.70 0.110306 0.389694 54 46
8 1.75 0.110306 0.389694 54 46
9 1.80 0.242424 0.257576 66 34
...

3.2.8 验证最佳分裂点的效果

# 10. 验证最佳分裂点的效果
print("步骤7: 验证最佳分裂点的效果")
left_labels = y_subset[X_subset <= best_threshold]
right_labels = y_subset[X_subset > best_threshold]
print(f"左节点类别分布: Versicolor: {sum(left_labels == 1)}, Virginica: {sum(left_labels == 2)}")
print(f"右节点类别分布: Versicolor: {sum(right_labels == 1)}, Virginica: {sum(right_labels == 2)}")
print(f"左节点基尼不纯度: {gini_impurity(left_labels):.6f}")
print(f"右节点基尼不纯度: {gini_impurity(right_labels):.6f}")

输出结果：

步骤7: 验证最佳分裂点的效果
左节点类别分布: Versicolor: 49, Virginica: 5
右节点类别分布: Versicolor: 1, Virginica: 45
bincount类别计数: [ 0 49 5], len: 54, 每个类别的占比: [0. 0.90740741 0.09259259]
左节点基尼不纯度: 0.168038
bincount类别计数: [ 0 1 45], len: 46, 每个类别的占比: [0. 0.02173913 0.97826087]
右节点基尼不纯度: 0.042533

3.3 为什么不是1.65

我们计算出的最佳阈值是1.7，并不是示例中的1.65，这是为什么呢，理论上讲，最佳分裂点确实应该是一个有区间变化的值。但在许多鸢尾花的教学示例中，它被固定为1.65，这主要是为了教学演示的稳定性和可重复性。在不同的情境下，这个分裂点会是会有细微的变化的。

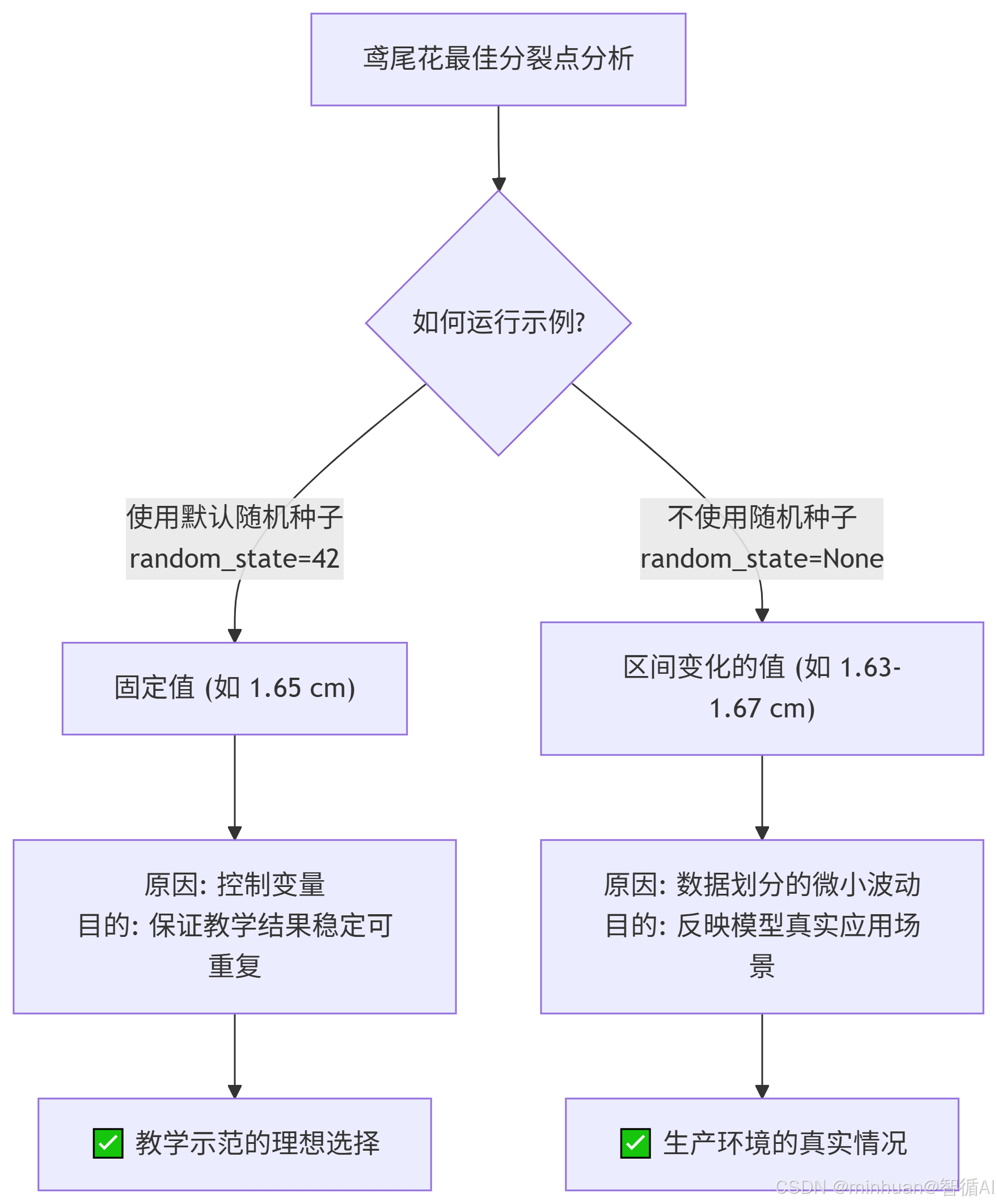
根本原因：记得前文我们说果的random_state 参数（随机种子）

如果固定 random_state（例如 random_state=42）：每次运行代码，数据都会以完全相同的方式被划分。因此，模型训练过程完全一致，找到的最佳分裂点也固定不变。
如果不固定 random_state（即 random_state=None）：每次运行代码，都会产生一个随机的划分。训练集的样本构成会有微小的不同，导致找到的“最佳”分裂点也在一个区间内波动（例如1.63cm, 1.65cm, 1.67cm）。
教学示例中固定 random_state，是为了确保所有学习者运行代码后都能得到完全一样的结果，便于教学和比较。

不同的训练子集会导致这个“最佳”点的微小波动：