吴恩达机器学习作业七：方差与偏差

数据集在作业一

方差与偏差

在机器学习中，偏差（Bias） 和方差（Variance） 是衡量模型泛化能力的两个核心概念，它们共同决定了模型的总误差。以下是具体定义：

1. 偏差（Bias）

• 定义：模型对训练数据中真实规律的偏离程度，即模型在平均意义上的预测值与真实值之间的差距。

• 本质：反映模型的拟合能力，由模型本身的简化假设（如线性模型假设数据是线性关系）导致。

• 示例：

  • 用线性模型拟合非线性分布的数据（如二次曲线关系），会因模型假设过于简单而产生高偏差，表现为训练误差和测试误差都较大（欠拟合）。

  • 复杂模型（如深度神经网络）通常偏差较低，因为它们能捕捉更复杂的规律。

1. 方差（Variance）

• 定义：模型对训练数据中随机噪声的敏感程度，即模型在不同训练数据集上的预测结果之间的波动范围。

• 本质：反映模型的稳定性，由模型对训练数据细节的过度关注导致。

• 示例：

  • 复杂模型（如高次多项式、未剪枝的决策树）可能过度拟合训练数据中的噪声，在不同训练集上的预测结果差异很大，即高方差，表现为训练误差很小但测试误差很大（过拟合）。

  • 简单模型（如线性回归）通常方差较低，因为它们对数据细节的敏感度低，预测更稳定。

高偏差：用线性模型拟合非线性分布的数据（如二次曲线关系），会因模型假设过于简单而产生高偏差，表现为训练误差和测试误差都较大（欠拟合）

高方差：复杂模型（如高次多项式、未剪枝的决策树）可能过度拟合训练数据中的噪声，在不同训练集上的预测结果差异很大，即高方差，表现为训练误差很小但测试误差很大（过拟合）。

这两个是我们要解决的问题。

解决方式

问题类型	核心原因	解决核心思路	典型手段
高偏差	模型太简单，无法拟合规律	增强拟合能力	复杂模型、增加特征、减少正则
高方差	模型太复杂，过度拟合噪声	降低敏感程度	简化模型、增加数据、加强正则

实际应用中，需通过交叉验证观察训练误差与验证误差的差距：

• 若两者都高且接近 → 高偏差（欠拟合）；

• 若训练误差低但验证误差高 → 高方差（过拟合），再针对性调整。

代码

读取数据

import  numpy as np
import matplotlib.pyplot as plt
from scipy.io import loadmat
from scipy.optimize import minimize# 读取数据
data=loadmat('ex5data1.mat')
# 训练集
X_train=data['X']
y_train=data['y']
# print(X_train.shape,y_train.shape)(12, 1) (12, 1)# 验证集
X_val=data['Xval']
y_val=data['yval']
# print(X_val.shape,y_val.shape)(21, 1) (21, 1)# 测试集
X_test=data['Xtest']
y_test=data['ytest']
# print(X_test.shape,y_test.shape)(21, 1) (21, 1)

预处理（加入截距）

# 加入截距
X_train=np.insert(X_train,0,values=1,axis=1)
X_val=np.insert(X_val,0,values=1,axis=1)
X_test=np.insert(X_test,0,values=1,axis=1)
# print(X_train.shape,X_val.shape,X_test.shape)

可视化

def plot_data(X,y):fig,ax=plt.subplots()ax.scatter(X[:,1],y)ax.set(xlabel='water level',ylabel='water flying out')plot_data(X_train,y_train)
# plt.show()

损失函数

def cost(theta,X,y):m=X.shape[0]h=np.dot(X,theta)cost=np.sum((h-y.flatten())**2)/(2*m)return costdef cost_reg(theta,X,y,lamda):m=X.shape[0]reg=np.sum(theta[1:]**2)*lamda/(2*m)return cost(theta,X,y)+reg

梯度

def reg_gradient(theta,X,y,lamda):m=X.shape[0]reg=theta[1:]*(lamda/m)reg=np.insert(reg,0,0,0)return np.dot(X.T,(np.dot(X,theta)-y.flatten()))/m+reg

参数训练

def train_model(X,y,lamda):theta=np.ones(X.shape[1])result=minimize(fun=cost_reg,x0=theta,args=(X,y,lamda),method='TNC',jac=reg_gradient)return result.x# 训练模型
theta_final=train_model(X_train,y_train,0)#[13.08790348  0.36777923]

这里是用method='TNC' 指的是使用 Truncated Newton Method（截断牛顿法）

拟合图像

fig,ax=plt.subplots()
plt.scatter(X_train[:,1],y_train,c='r',marker='x')
plt.xlabel('Change in water level (x)')
plt.ylabel('Water flowing out of the dam (y)')
plt.plot(X_train[:,1],np.dot(X_train,theta_final),c='b')
plt.show()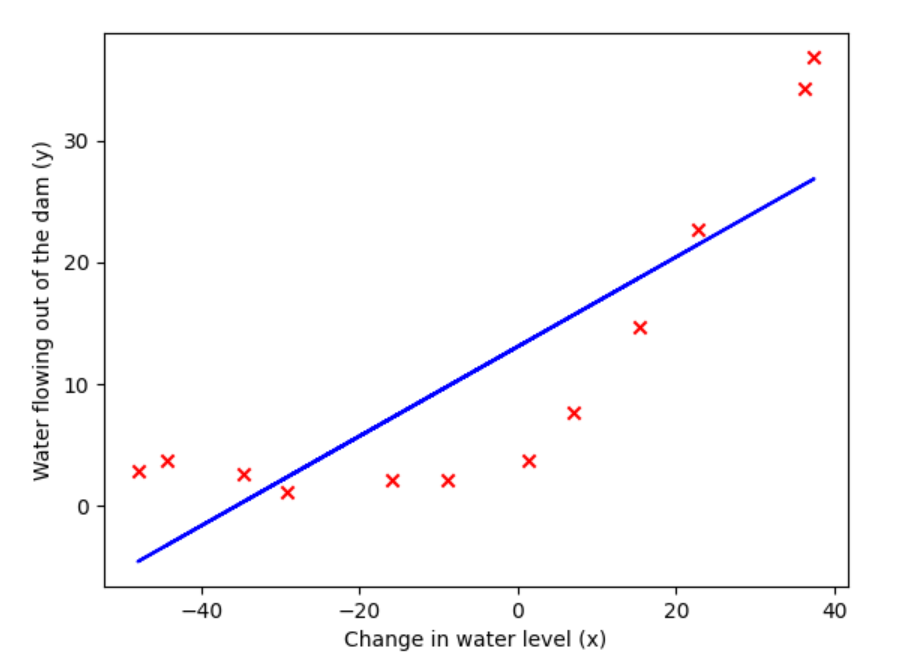

画学习曲线，判断高偏差，高方差问题

"""学习曲线通过绘制训练集损失，验证集损失随训练样本增加的变化趋势，来判断模型的偏差和方差问题

高偏差（欠拟合）：训练集损失和验证集损失都较高，且两者差距很小（几乎重合）

高方差（过拟合）：训练集损失很低（模型几乎完美拟合训练数据），但验证集损失显著高于训练集损失，且两者差距较大。"""

def plot_learning_curve(X_train,y_train,X_val,y_val,lamda):m=X_train.shape[0]train_cost=[]cv_cost=[]for i in range(1,m+1):theta=train_model(X_train[:i],y_train[:i],lamda)train_cost.append(cost(theta,X_train[:i],y_train[:i]))cv_cost.append(cost(theta,X_val,y_val))plt.plot(np.arange(1,m+1),train_cost,c='r',label='Train')plt.plot(np.arange(1,m+1),cv_cost,c='b',label='Cross Validation')plt.xlabel('Number of training examples')plt.ylabel('costs')plt.legend()plt.show()# plot_learning_curve(X_train,y_train,X_val,y_val,0)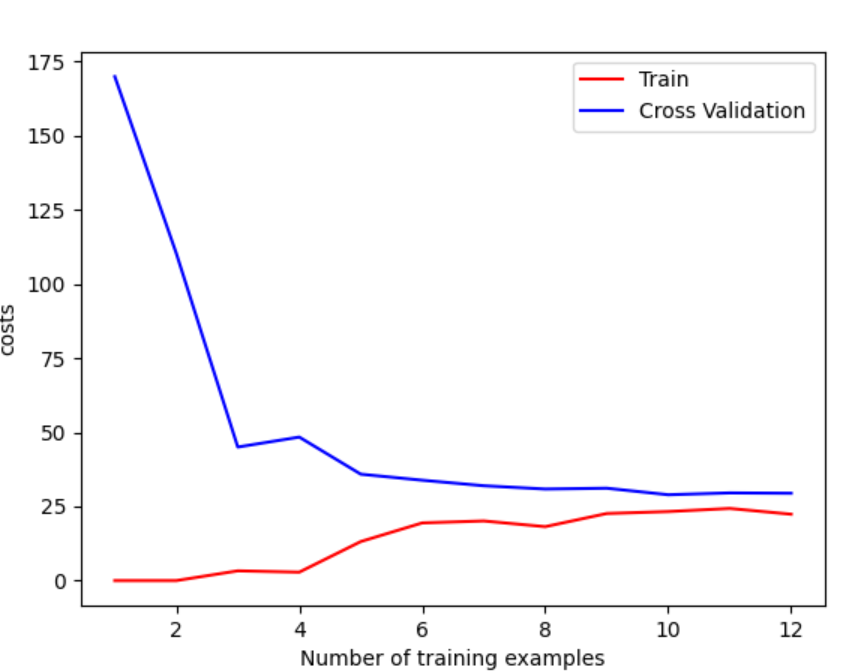

虽然随着训练量的增大，损失出现下降，但可以看出，二者损失都较大，高偏差，因此需要特征映射创造多项式特征，进行多项式回归，用更复杂的函数去拟合

特征映射，均值归一化

def poly_features(X,power):for i in range(2,power+1):X=np.insert(X,X.shape[1],np.power(X[:,1],i),axis=1)return X

这里的特征映射就是创造多项式特征，而均值归一化的目的是为了缓解高阶项对训练的影响。

举个直观例子：

• 特征 1：“房屋面积”（数值范围：50~200 平方米）；
• 特征 2：“房间数”（数值范围：1~5 个）；
• 特征 3（高阶项）：“面积的平方”（数值范围：2500~40000 平方米 ²）。

若不做归一化，“面积平方” 的数值会远大于 “房间数”，导致模型在更新参数时（如梯度下降），会过度偏向 “数值大的特征（高阶项）”—— 参数更新幅度受特征数值尺度主导，而非特征对目标的实际影响，最终导致训练效率低（收敛慢）或参数优化不稳定。

初始化参数（数据预处理）

power=6
# 特征映射
X_train_poly=poly_features(X_train,power)
X_val_poly=poly_features(X_val,power)
X_test_poly=poly_features(X_test,power)
# 均值归一化
mu,sigma=get_standard(X_train_poly)
X_train_norms=feature_normalize(X_train_poly,mu,sigma)
X_val_norms=feature_normalize(X_val_poly,mu,sigma)
X_test_norms=feature_normalize(X_test_poly,mu,sigma)

训练

# 训练模型
theta_final=train_model(X_train_norms,y_train,0)

绘制曲线

plot_data(X_train,y_train)
# 绘制曲线
def plot_poly_curve():x=np.linspace(-60,60,100)X_reshape=x.reshape((x.shape[0],1))X_reshape=np.insert(X_reshape,0,1,axis=1)X_reshape=poly_features(X_reshape,power)X_reshape=feature_normalize(X_reshape,mu,sigma)plt.plot(x,np.dot(X_reshape,theta_final),c='r')plt.show()# plot_poly_curve()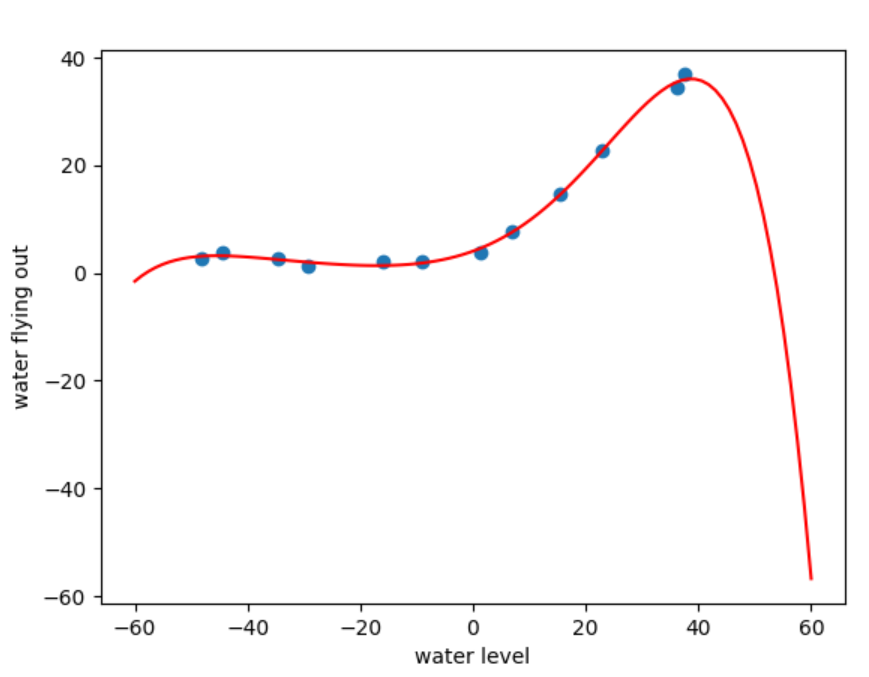

用交叉验证集选择lmd（惩罚系数）

lamdas=[0,0.001,0.003,0.01,0.03,0.1,0.3,1,3,10]
train_costs=[]
cv_costs=[]
for lamda in lamdas:theta_final=train_model(X_train_norms,y_train,lamda)train_costs.append(cost(theta_final,X_train_norms,y_train))cv_costs.append(cost(theta_final,X_val_norms,y_val))
plt.plot(lamdas,train_costs,c='r',label='Train')
plt.plot(lamdas,cv_costs,c='b',label='Cross Validation')
plt.xlabel('lamda')
plt.ylabel('costs')
plt.legend()
plt.show()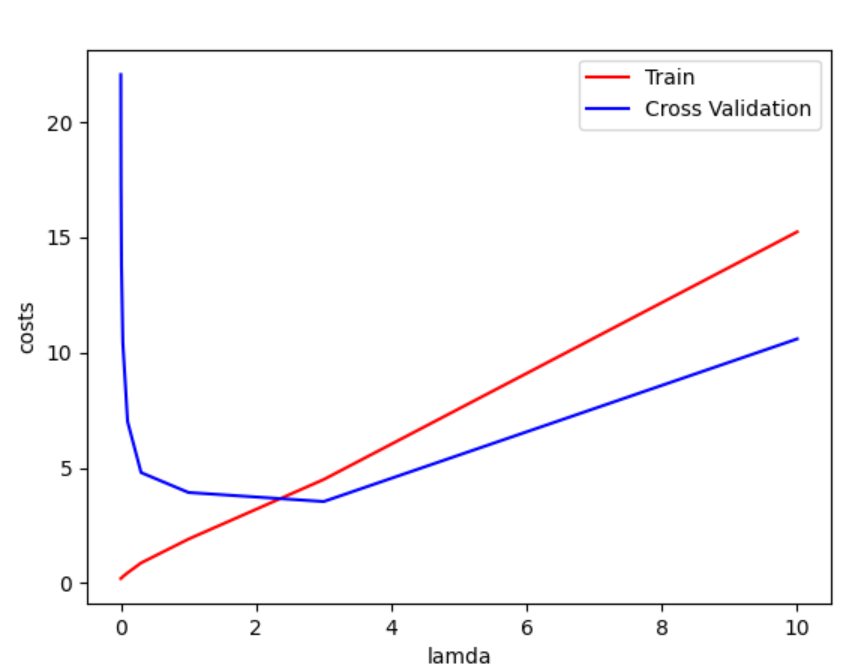

取出最佳lamda并训练模型

# 获取最佳lamda
best_lamda=lamdas[np.argmin(cv_costs)]
print(best_lamda)#3
# 训练最佳模型
theta_final=train_model(X_train_norms,y_train,best_lamda)
print(cost(theta_final,X_test_norms,y_test))
#4.39761601408022

总结

读取数据——预处理（加入偏置）——损失函数——梯度——调用优化器——拟合——特征映射，均值归一化——训练——找到最佳参数