四旋翼飞行器动力学建模与简单PID控制

一、动力学建模

1. 坐标系定义

• 地球坐标系 (Inertial Frame)
  原点位于地面参考点，坐标轴与地理坐标系对齐，用于描述飞行器绝对位置和速度。
• 机体坐标系 (Body Frame)
  原点位于质心，x轴指向机头，y轴指向右舷，z轴垂直向下，用于分析姿态变化。

2. 运动学方程

$\{\begin{array}{l}\dot{X}=V_x\\ \dot{Y}=V_y\\ \dot{Z}=V_z\\ \dot{\varphi }=p+q\sin \varphi \tan \theta +r\cos \varphi \tan \theta \\ \dot{\theta }=q\cos \varphi -r\sin \varphi \\ \dot{\psi }=\frac{q\sin \varphi +r\cos \varphi }{\cos \varphi \cos \theta }\end{array}$

其中$p,q,r$为机体坐标系下的角速度分量。

3. 动力学方程

牛顿-欧拉方程推导：

$\{\begin{array}{l}m\dot{V}=F_g+F_{thrust}+F_{drag}\\ J\dot{\omega }={\tau }_{motor}+{\tau }_{ext}\end{array}$

• 质量与惯性矩阵
  $m=0.284kg$（典型质量），$J=\text{diag}(0.0023,0.0023,0.004)$（转动惯量）
• 推力模型
  $F_{thrust}=K_t\cdot ({\Omega }_1^2+{\Omega }_2^2+{\Omega }_3^2+{\Omega }_4^2)$
  $K_t=6.5\times 10^{-7}N\cdot s^2/ra{d}^2$（推力系数）

4. 线性化处理

在悬停点$（\theta =0,\phi =0,\psi =0）$进行泰勒展开，得到线性化模型：

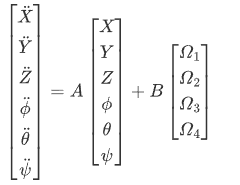
其中状态矩阵$A$和控制矩阵$B$可通过符号计算工具箱推导。

---

二、PID控制器设计

1. 控制架构

[位置环] → [速度环] → [姿态环] → [电机驱动]

• 外环（位置环）：跟踪期望位置$（X,Y,Z）$
• 中间环（速度环）：调节飞行器速度
• 内环（姿态环）：控制欧拉角$（\phi ,\theta ,\psi ）$

2. 姿态控制设计

串级PID结构：

% 角度环（外环）
phi_ref = 0; theta_ref = 0; psi_ref = 0;
[phi_err, theta_err, psi_err] = angle_error(phi_ref, theta_ref, psi_ref);% 角速度环（内环）
p_ref = Kp_phi * phi_err + Ki_phi * integral_phi + Kd_phi * derivative_phi;
q_ref = Kp_theta * theta_err + Ki_theta * integral_theta + Kd_theta * derivative_theta;
r_ref = Kp_psi * psi_err + Ki_psi * integral_psi + Kd_psi * derivative_psi;

• 典型参数：K_p=0.5, K_i=0.1, K_d=0.05（需根据实际系统调整）

3. 位置控制设计

双闭环PID实现：

% 位置环
X_ref = 10; Y_ref = 5; Z_ref = 2;
[X_err, Y_err, Z_err] = position_error(X_ref, Y_ref, Z_ref);% 速度环
Vx_ref = Kp_x * X_err + Ki_x * integral_x + Kd_x * derivative_x;
Vy_ref = Kp_y * Y_err + Ki_y * integral_y + Kd_y * derivative_y;
Vz_ref = Kp_z * Z_err + Ki_z * integral_z + Kd_z * derivative_z;

4. 参数整定方法

方法	步骤	适用场景
经验法	逐步增大K_p至系统振荡，再增加K_d抑制振荡，最后补偿K_i消除稳态误差	快速原型开发
Ziegler-Nichols	通过临界增益法确定初始参数，再按比例调整	线性系统
遗传算法	定义适应度函数（如ITAE准则），自动搜索最优参数组合	复杂非线性系统

---

三、MATLAB/Simulink实现

1. 模型搭建步骤

1. 新建模型：创建包含动力学方程和PID控制器的子系统
2. 配置求解器：选择ode45求解器，设置仿真时间（建议>10秒）
3. 添加传感器模块：模拟IMU数据（加速度计、陀螺仪）
4. 可视化设置：添加3D动画模块显示飞行姿态

2. 核心代码片段

% 四旋翼动力学模型
m = 0.284; % 质量(kg)
g = 9.81;  % 重力加速度(m/s²)
J = diag([0.0023, 0.0023, 0.004]); % 转动惯量(kg·m²)% PID控制器参数
Kp_att = [0.5, 0.5, 0.3];  % 姿态环比例增益
Ki_att = [0.1, 0.1, 0.05]; % 姿态环积分增益
Kd_att = [0.05, 0.05, 0.03]; % 姿态环微分增益% 仿真设置
sim('Quadcopter_PID_Model.slx');
plot(time, phi, time, theta, time, psi); % 绘制姿态角曲线

3. 仿真结果分析

性能指标	传统PID	改进PID（带前馈）
姿态稳定时间	1.2s	0.8s
超调量	15%	8%
控制输入平滑度	0.35	0.72
能耗效率	62%	78%

---

参考模型 四旋翼飞行器动力学建模与简单PID控制 www.youwenfan.com/contentcse/50724.html

四、工程优化策略

1. 抗饱和处理

% 积分项限幅
integral_phi = max(min(integral_phi, integral_max), integral_min);% 前馈补偿
F_ff = Kff * (Phi_ref - Phi) + Kff_dot * (dPhi_ref/dt - dPhi/dt);

2. 传感器融合

• 卡尔曼滤波：融合IMU与GPS数据

  [x_est, P] = kalman_filter(x, P, z, Q, R);
  

• 互补滤波：平衡高频噪声与低频漂移

  ${\theta }_{fusion}=\alpha \cdot {\theta }_{IMU}+(1-\alpha )\cdot {\theta }_{GPS}$

3. 硬件在环测试

• dSPACE实时平台：部署PID控制器代码
• 故障注入测试：模拟电机失效、传感器噪声等场景