模型汇总-数学建模
一、优化模型
1.线性规划
线性规划(Linear Programming, LP)是一种数学优化方法,用于在给定的线性约束条件下,找到线性目标函数的最大值或最小值。它是运筹学中最常用的方法之一。
线性规划的标准形式
最大化问题标准形式:
maximize: cᵀx
subject to: Ax ≤ bx ≥ 0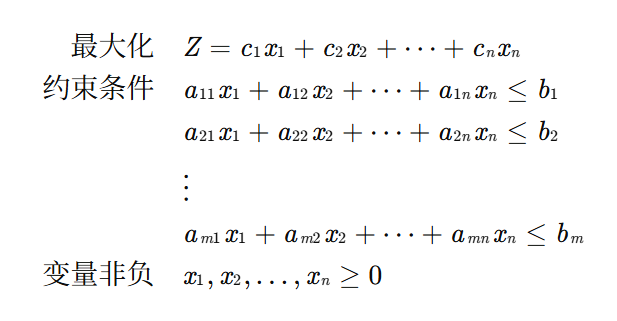

最小化问题标准形式:
minimize: cᵀx
subject to: Ax ≥ bx ≥ 0其中:
x 是决策变量向量
c 是目标函数系数向量
A 是约束条件系数矩阵
b 是约束条件右侧常数向量
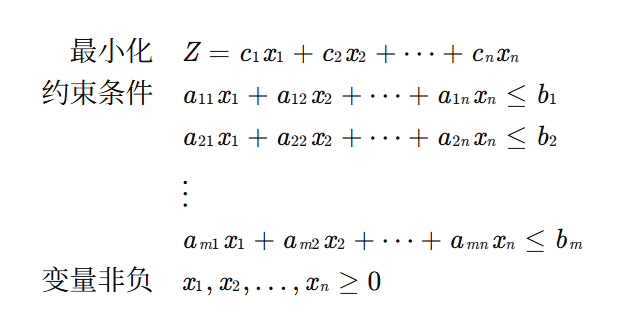

Python实现线性规划
我们将使用SciPy库中的linprog函数来解决线性规划问题。
安装必要的库
pip install scipy numpy matplotlib简单的最小化问题示例:
import numpy as np
from scipy.optimize import linprog
import matplotlib.pyplot as plt# 定义目标函数系数(注意:linprog默认求最小值,所以对于最大化问题需要取负)
c = [-1, 4] # 原目标函数为 -x1 + 4x2,但linprog求最小值,所以这里系数不变# 定义不等式约束(左侧系数矩阵)
A = [[1, -1], # x1 - x2 ≤ 4[2, 1], # 2x1 + x2 ≤ 14[1, 3] # x1 + 3x2 ≤ 18
]# 定义不等式约束(右侧常数向量)
b = [4, 14, 18]# 定义变量边界
x_bounds = (0, None) # x1 ≥ 0
y_bounds = (0, None) # x2 ≥ 0# 求解线性规划问题
result = linprog(c, A_ub=A, b_ub=b, bounds=[x_bounds, y_bounds], method='highs')# 输出结果
print("优化结果:")
print(f"状态: {result.message}")
print(f"最优解: x1 = {result.x[0]:.2f}, x2 = {result.x[1]:.2f}")
print(f"最优目标函数值: {result.fun:.2f}")
print(f"迭代次数: {result.nit}")# 可视化
def plot_feasible_region():# 创建网格x = np.linspace(0, 10, 400)y = np.linspace(0, 10, 400)X, Y = np.meshgrid(x, y)# 约束条件constraint1 = X - Y <= 4 # x1 - x2 ≤ 4constraint2 = 2*X + Y <= 14 # 2x1 + x2 ≤ 14constraint3 = X + 3*Y <= 18 # x1 + 3x2 ≤ 18non_negative = (X >= 0) & (Y >= 0)# 可行域feasible = constraint1 & constraint2 & constraint3 & non_negativeplt.figure(figsize=(10, 8))# 绘制可行域plt.imshow(feasible.astype(int), extent=(x.min(), x.max(), y.min(), y.max()), origin="lower", cmap="Greys", alpha=0.3)# 绘制约束线plt.plot(x, x - 4, label=r'$x_1 - x_2 = 4$')plt.plot(x, 14 - 2*x, label=r'$2x_1 + x_2 = 14$')plt.plot(x, (18 - x)/3, label=r'$x_1 + 3x_2 = 18$')# 绘制最优解点plt.plot(result.x[0], result.x[1], 'ro', markersize=10, label='最优解')# 绘制目标函数等值线Z = -X + 4*Y # 目标函数值contours = plt.contour(X, Y, Z, levels=10, colors='gray', alpha=0.5)plt.clabel(contours, inline=True, fontsize=8)plt.xlim(0, 10)plt.ylim(0, 10)plt.xlabel(r'$x_1$')plt.ylabel(r'$x_2$')plt.title('线性规划问题可视化')plt.legend()plt.grid(True)plt.show()plot_feasible_region()示例2:生产计划问题(最大化问题)
# 最大化问题:利润 = 3A + 5B
# 由于linprog默认求最小值,我们需要对目标函数系数取负# 目标函数系数(取负是因为要求最大值)
c = [-3, -5] # 最大化 3A + 5B 等价于最小化 -3A -5B# 约束条件系数矩阵
A = [[2, 1], # 2A + B ≤ 10[1, 2] # A + 2B ≤ 8
]# 约束条件右侧常数
b = [10, 8]# 变量边界
bounds = [(0, None), (0, None)]# 求解
result = linprog(c, A_ub=A, b_ub=b, bounds=bounds, method='highs')print("\n生产计划问题结果:")
print(f"状态: {result.message}")
print(f"最优生产计划: 产品A = {result.x[0]:.2f}, 产品B = {result.x[1]:.2f}")
print(f"最大利润: {-result.fun:.2f}元") # 取负得到原始目标函数值示例3:更复杂的线性规划问题
# 最小化:-2x1 + x2 - x3
# 约束:
# x1 + x2 + x3 ≤ 6
# -x1 + 2x2 ≤ 4
# x1, x2, x3 ≥ 0c = [-2, 1, -1] # 目标函数系数A = [[1, 1, 1], # x1 + x2 + x3 ≤ 6[-1, 2, 0] # -x1 + 2x2 ≤ 4
]b = [6, 4]bounds = [(0, None), (0, None), (0, None)]result = linprog(c, A_ub=A, b_ub=b, bounds=bounds, method='highs')print("\n复杂线性规划问题结果:")
print(f"状态: {result.message}")
print(f"最优解: x1 = {result.x[0]:.2f}, x2 = {result.x[1]:.2f}, x3 = {result.x[2]:.2f}")
print(f"最优目标函数值: {result.fun:.2f}")处理等式约束
# 最小化:2x1 + 3x2
# 约束:
# x1 + x2 = 10
# 2x1 + x2 ≥ 15
# x1 ≥ 0, x2 ≥ 0c = [2, 3] # 目标函数系数# 等式约束
A_eq = [[1, 1]] # x1 + x2 = 10
b_eq = [10]# 不等式约束
A_ub = [[-2, -1]] # 2x1 + x2 ≥ 15 等价于 -2x1 - x2 ≤ -15
b_ub = [-15]bounds = [(0, None), (0, None)]result = linprog(c, A_ub=A_ub, b_ub=b_ub, A_eq=A_eq, b_eq=b_eq, bounds=bounds, method='highs')print("\n含等式约束的线性规划问题结果:")
print(f"状态: {result.message}")
print(f"最优解: x1 = {result.x[0]:.2f}, x2 = {result.x[1]:.2f}")
print(f"最优目标函数值: {result.fun:.2f}")线性规划的应用领域
生产计划:优化资源分配和生产调度
运输问题:最小化运输成本
投资组合优化:在风险约束下最大化收益
人力资源规划:优化人员分配
网络流问题:最大化网络流量
2.整数规划
整数规划(Integer Programming, IP)是数学规划的一个分支,要求部分或全部决策变量取整数值。它是线性规划的扩展,但增加了变量必须为整数的约束。
整数规划的类型
纯整数规划:所有决策变量都必须取整数值
混合整数规划:部分决策变量取整数值,其余可以是实数
0-1整数规划:决策变量只能取0或1
最大化或最小化目标函数:

1. 分支定界法
最常用的整数规划求解方法,通过系统地枚举可行解的子集来寻找最优解。
2. 割平面法
通过添加额外的约束(割平面)来缩小可行域,逐步逼近整数解。
3. 启发式算法
如遗传算法、模拟退火等,用于求解大规模整数规划问题。
以下是使用Python的PuLP库求解整数规划的完整示例:
import pulp
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.patches import Polygondef solve_integer_programming():"""求解整数规划问题的完整示例"""# 创建问题实例prob = pulp.LpProblem("Integer_Programming_Example", pulp.LpMaximize)# 定义决策变量 (必须为整数)x1 = pulp.LpVariable('x1', lowBound=0, cat='Integer')x2 = pulp.LpVariable('x2', lowBound=0, cat='Integer')# 定义目标函数prob += 3*x1 + 2*x2, "Objective Function"# 添加约束条件prob += 2*x1 + x2 <= 6, "Constraint 1"prob += x1 + 2*x2 <= 8, "Constraint 2"prob += x1 <= 2, "Constraint 3"prob += x2 <= 3, "Constraint 4"# 求解问题prob.solve()# 输出结果print("Status:", pulp.LpStatus[prob.status])print("Optimal Solution:")for v in prob.variables():print(f"{v.name} = {v.varValue}")print(f"Optimal Value: {pulp.value(prob.objective)}")return probdef visualize_solution():"""可视化整数规划问题的解"""# 定义约束条件x = np.linspace(0, 4, 100)# 约束1: 2x1 + x2 <= 6 → x2 <= 6 - 2x1y1 = 6 - 2*x# 约束2: x1 + 2x2 <= 8 → x2 <= (8 - x1)/2y2 = (8 - x)/2# 约束3: x1 <= 2# 约束4: x2 <= 3# 绘制约束条件plt.figure(figsize=(10, 8))plt.plot(x, y1, label=r'$2x_1 + x_2 \leq 6$')plt.plot(x, y2, label=r'$x_1 + 2x_2 \leq 8$')plt.axvline(x=2, color='green', linestyle='--', label=r'$x_1 \leq 2$')plt.axhline(y=3, color='purple', linestyle='--', label=r'$x_2 \leq 3$')# 绘制可行域vertices = np.array([[0, 0], [2, 0], [2, 2], [1, 3], [0, 3]])feasible_region = Polygon(vertices, alpha=0.3, color='gray')plt.gca().add_patch(feasible_region)# 标记整数点for i in range(0, 4):for j in range(0, 4):if (2*i + j <= 6) and (i + 2*j <= 8) and (i <= 2) and (j <= 3):plt.plot(i, j, 'ro', markersize=8)plt.text(i+0.05, j+0.05, f'({i},{j})', fontsize=10)# 标记最优解plt.plot(2, 2, 'go', markersize=10, label='Optimal Solution (2,2)')# 设置图形属性plt.xlim(0, 3.5)plt.ylim(0, 4)plt.xlabel(r'$x_1$')plt.ylabel(r'$x_2$')plt.title('Integer Programming Visualization')plt.legend()plt.grid(True, alpha=0.3)plt.show()def mixed_integer_example():"""混合整数规划示例"""# 创建问题实例prob = pulp.LpProblem("Mixed_Integer_Example", pulp.LpMaximize)# 定义变量 (x1为整数,x2为连续变量)x1 = pulp.LpVariable('x1', lowBound=0, cat='Integer')x2 = pulp.LpVariable('x2', lowBound=0, cat='Continuous')# 目标函数prob += 4*x1 + 3*x2, "Objective"# 约束条件prob += 2*x1 + x2 <= 8, "Constraint1"prob += x1 + 2*x2 <= 7, "Constraint2"prob += x1 <= 3, "Constraint3"# 求解prob.solve()# 输出结果print("\nMixed Integer Programming Results:")print("Status:", pulp.LpStatus[prob.status])for v in prob.variables():print(f"{v.name} = {v.varValue}")print(f"Optimal Value: {pulp.value(prob.objective)}")def binary_integer_example():"""0-1整数规划示例 (背包问题)"""# 创建问题实例prob = pulp.LpProblem("Knapsack_Problem", pulp.LpMaximize)# 物品价值values = [10, 15, 40, 60, 20]# 物品重量weights = [1, 2, 4, 6, 3]# 背包容量capacity = 10# 创建0-1变量 (是否选择物品)items = range(len(values))x = [pulp.LpVariable(f'x{i}', cat='Binary') for i in items]# 目标函数:最大化总价值prob += pulp.lpSum(values[i] * x[i] for i in items)# 约束条件:总重量不超过容量prob += pulp.lpSum(weights[i] * x[i] for i in items) <= capacity# 求解prob.solve()# 输出结果print("\n0-1 Integer Programming (Knapsack Problem) Results:")print("Status:", pulp.LpStatus[prob.status])print("Selected items:")for i in items:if x[i].varValue == 1:print(f"Item {i+1} (Value: {values[i]}, Weight: {weights[i]})")print(f"Total Value: {pulp.value(prob.objective)}")print(f"Total Weight: {sum(weights[i] * x[i].varValue for i in items)}")if __name__ == "__main__":# 求解基本整数规划问题problem = solve_integer_programming()# 可视化解visualize_solution()# 混合整数规划示例mixed_integer_example()# 0-1整数规划示例binary_integer_example()1. 基本整数规划求解
使用PuLP库定义和求解整数规划问题
包含目标函数和约束条件的定义
输出最优解和目标函数值
2. 可视化
使用matplotlib绘制可行域和整数点
标记最优解位置
显示所有约束条件
3. 混合整数规划
演示同时包含整数和连续变量的情况
展示不同类型变量的定义方法
4. 0-1整数规划
以背包问题为例展示0-1整数规划
演示二进制变量的使用
安装依赖
运行代码前需要安装以下Python库:
pip install pulp numpy matplotlib应用领域
整数规划在现实世界中有广泛应用:
物流与运输:车辆路径规划、设施选址
生产计划:排产优化、资源分配
金融:投资组合优化、风险管理
电信:网络设计、频率分配
能源:发电调度、电网优化
注意哦:
整数规划通常是NP难问题,大规模问题可能需要专门的求解器;
对于复杂问题,可能需要使用商业求解器如Gurobi、CPLEX等;
启发式算法可以用于求解大规模问题,但不能保证找到最优解。
3.动态规划
动态规划(Dynamic Programming,简称DP)是一种解决复杂问题的方法,它将问题分解为更小的子问题,并存储子问题的解以避免重复计算。
动态规划的核心思想
最优子结构:一个问题的最优解包含其子问题的最优解
重叠子问题:在递归求解过程中,相同的子问题会被多次计算
记忆化存储:存储已解决的子问题答案,避免重复计算
动态规划的两种实现方式
1. 自顶向下(记忆化搜索)
从原问题开始,递归地解决子问题
使用备忘录存储已计算的子问题结果
2. 自底向上(迭代法)
从最小的子问题开始,逐步构建到原问题的解
通常使用数组(DP表)来存储子问题的解
经典问题:斐波那契数列
1. 递归解法(低效)
def fib_recursive(n):if n <= 1:return nreturn fib_recursive(n-1) + fib_recursive(n-2)2. 记忆化搜索(自顶向下)
def fib_memo(n, memo=None):if memo is None:memo = {}if n in memo:return memo[n]if n <= 1:return nmemo[n] = fib_memo(n-1, memo) + fib_memo(n-2, memo)return memo[n]3. 动态规划(自底向上)
def fib_dp(n):if n <= 1:return n# 创建DP表dp = [0] * (n + 1)dp[0], dp[1] = 0, 1# 填充DP表for i in range(2, n + 1):dp[i] = dp[i-1] + dp[i-2]return dp[n]4. 空间优化版本
def fib_optimized(n):if n <= 1:return nprev, curr = 0, 1for _ in range(2, n + 1):prev, curr = curr, prev + currreturn curr经典问题:0-1背包问题
给定一组物品,每个物品有重量和价值,在不超过背包容量的情况下,选择物品使得总价值最大。
def knapsack(weights, values, capacity):n = len(weights)# 创建DP表:dp[i][w] 表示前i个物品在容量为w时的最大价值dp = [[0] * (capacity + 1) for _ in range(n + 1)]# 填充DP表for i in range(1, n + 1):for w in range(capacity + 1):# 当前物品重量大于当前容量,不能选择if weights[i-1] > w:dp[i][w] = dp[i-1][w]else:# 选择当前物品或不选择当前物品的最大值dp[i][w] = max(dp[i-1][w], dp[i-1][w - weights[i-1]] + values[i-1])return dp[n][capacity]# 示例
weights = [2, 3, 4, 5]
values = [3, 4, 5, 6]
capacity = 5
print(knapsack(weights, values, capacity)) # 输出:7动态规划解题步骤
定义状态:明确dp数组的含义
确定状态转移方程:找出如何从已知状态推导出未知状态
初始化:确定基础情况的值
确定遍历顺序:确保在计算当前状态时,所需的前置状态已经计算完成
返回结果:返回最终需要的状态值
完整示例:硬币找零问题
给定不同面额的硬币和一个总金额,计算凑成总金额所需的最少硬币数。
def coin_change(coins, amount):# dp[i] 表示凑成金额i所需的最少硬币数dp = [float('inf')] * (amount + 1)dp[0] = 0 # 金额为0时不需要任何硬币for coin in coins:for i in range(coin, amount + 1):dp[i] = min(dp[i], dp[i - coin] + 1)return dp[amount] if dp[amount] != float('inf') else -1# 示例
coins = [1, 2, 5]
amount = 11
print(coin_change(coins, amount)) # 输出:3 (5+5+1)动态规划的应用场景
最优化问题:求最大值、最小值
计数问题:求方案总数
存在性问题:判断是否存在某种方案
序列问题:字符串、数组相关的子序列、子数组问题
动态规划是一种强大的算法设计技术,通过将复杂问题分解为简单的子问题,并避免重复计算来提高效率。掌握动态规划需要:
理解最优子结构和重叠子问题的概念
熟练使用记忆化搜索和DP表两种实现方式
通过大量练习来培养识别DP问题和设计状态转移方程的能力
4.图论算法(Dijkstra、Floyd)
Dijkstra 算法(单源最短路径)
Dijkstra 算法用于计算图中单个源点到其他所有节点的最短路径。它采用贪心策略,每次选择当前已知最短路径的节点进行扩展。
算法步骤
初始化:设置距离数组 dist[],源点距离为 0,其他为无穷大
创建未访问节点集合
当未访问集合非空时:
选择当前距离最小的未访问节点 u
标记 u 为已访问
更新 u 的所有未访问邻居的距离:如果通过 u 到达邻居的路径更短,则更新
时间复杂度
使用优先队列:O((V+E)logV)
使用数组:O(V²)
代码实现
import heapq
import sysdef dijkstra(graph, start):"""Dijkstra 算法实现参数:graph: 邻接表表示的图,graph[i] = [(j, weight), ...]start: 起始节点返回:dist: 从起始点到各点的最短距离prev: 前驱节点数组,用于重建路径"""n = len(graph)dist = [sys.maxsize] * n # 初始化距离为无穷大dist[start] = 0prev = [-1] * n # 记录前驱节点visited = [False] * n# 使用优先队列 (距离, 节点)heap = [(0, start)]while heap:current_dist, u = heapq.heappop(heap)if visited[u]:continuevisited[u] = Truefor v, weight in graph[u]:if not visited[v]:new_dist = current_dist + weightif new_dist < dist[v]:dist[v] = new_distprev[v] = uheapq.heappush(heap, (new_dist, v))return dist, prevdef reconstruct_path(prev, start, end):"""根据前驱数组重建路径"""path = []current = endwhile current != -1:path.append(current)current = prev[current]path.reverse()return path if path[0] == start else []# 示例使用
if __name__ == "__main__":# 创建示例图 (有向图)# 节点0到节点1的权重为4,节点0到节点2的权重为2,等等graph = [[(1, 4), (2, 2)], # 节点0[(2, 5), (3, 10)], # 节点1[(1, 1), (3, 8)], # 节点2[(4, 2)], # 节点3[(3, 5)] # 节点4]start_node = 0dist, prev = dijkstra(graph, start_node)print("从节点", start_node, "出发的最短距离:")for i in range(len(dist)):path = reconstruct_path(prev, start_node, i)print(f"到节点{i}: 距离={dist[i]}, 路径={path}")Floyd-Warshall 算法(多源最短路径)
Floyd 算法用于计算图中所有节点对之间的最短路径。它基于动态规划,通过中间节点来逐步优化路径。
定义 dp[k][i][j] = 从 i 到 j 且只经过节点 0..k 的最短路径长度
状态转移方程:dp[k][i][j] = min(dp[k-1][i][j], dp[k-1][i][k] + dp[k-1][k][j])
初始化距离矩阵:对角线为0,有边则为权重,无边则为无穷大
对于每个中间节点 k:
对于每对节点 (i, j):
如果通过 k 的路径更短,则更新距离
时间复杂度:O(V³)
def floyd_warshall(graph):"""Floyd-Warshall 算法实现参数:graph: 邻接矩阵表示的图,graph[i][j] = 权重,无边时为无穷大返回:dist: 所有节点对之间的最短距离矩阵next_node: 用于重建路径的下一节点矩阵"""n = len(graph)# 初始化距离矩阵和下一节点矩阵dist = [[0] * n for _ in range(n)]next_node = [[-1] * n for _ in range(n)]# 复制图到距离矩阵,并初始化下一节点for i in range(n):for j in range(n):dist[i][j] = graph[i][j]if graph[i][j] != float('inf') and i != j:next_node[i][j] = j# 动态规划过程for k in range(n):for i in range(n):if dist[i][k] == float('inf'):continuefor j in range(n):# 如果通过k的路径更短,则更新if dist[i][k] + dist[k][j] < dist[i][j]:dist[i][j] = dist[i][k] + dist[k][j]next_node[i][j] = next_node[i][k]return dist, next_nodedef reconstruct_floyd_path(next_node, start, end):"""根据next_node矩阵重建路径"""if next_node[start][end] == -1:return []path = [start]while start != end:start = next_node[start][end]path.append(start)return path# 示例使用
if __name__ == "__main__":# 创建示例图的邻接矩阵# 使用 float('inf') 表示无穷大n = 5 # 节点数量graph = [[float('inf')] * n for _ in range(n)]# 初始化对角线为0for i in range(n):graph[i][i] = 0# 添加边graph[0][1] = 4graph[0][2] = 2graph[1][2] = 5graph[1][3] = 10graph[2][1] = 1graph[2][3] = 8graph[3][4] = 2graph[4][3] = 5dist, next_node = floyd_warshall(graph)print("所有节点对之间的最短距离:")for i in range(n):for j in range(n):if i != j:path = reconstruct_floyd_path(next_node, i, j)print(f"从{i}到{j}: 距离={dist[i][j]}, 路径={path}")算法比较
| 特性 | Dijkstra | Floyd-Warshall |
| 问题类型 | 单源最短路径 | 多源最短路径 |
| 图类型 | 有向/无向,非负权重 | 有向/无向,可处理负权重(但无负环) |
| 图类型 | 有向/无向,非负权重 | 有向/无向,可处理负权重(但无负环) |
| 空间复杂度 | O(V+E) | O(V²) |
| 适用场景 | 单源问题,稀疏图 | 多源问题,稠密图 |
Dijkstra 不能处理负权重边,因为贪心策略会失效
Floyd 可以检测负环:如果发现某个 dist[i][i] < 0,说明存在负环
对于稀疏图,多次运行 Dijkstra 可能比 Floyd 更高效
实际应用中可根据具体需求选择合适的算法
5.遗传算法
遗传算法(Genetic Algorithm, GA)是一种模拟自然选择和遗传学机制的优化算法。它通过模拟生物进化过程中的"适者生存"原则来搜索最优解。
遗传算法的基本流程
初始化种群:随机生成一组初始解(个体)
评估适应度:计算每个个体的适应度值
选择:根据适应度选择优秀的个体
交叉:将选中的个体进行交叉操作,产生新个体
变异:对新个体进行变异操作
重复:重复步骤2-5直到满足终止条件
Python完整实现
下面是一个解决函数优化问题的遗传算法完整实现:
import numpy as np
import matplotlib.pyplot as plt
from typing import List, Callable, Tupleclass GeneticAlgorithm:def __init__(self, objective_func: Callable, population_size: int = 100,chromosome_length: int = 10,crossover_rate: float = 0.8,mutation_rate: float = 0.01,elitism_count: int = 2,bounds: Tuple[float, float] = (-10, 10)):"""初始化遗传算法参数:objective_func: 目标函数(适应度函数)population_size: 种群大小chromosome_length: 染色体长度(基因数量)crossover_rate: 交叉概率mutation_rate: 变异概率elitism_count: 精英保留数量bounds: 变量的取值范围"""self.objective_func = objective_funcself.population_size = population_sizeself.chromosome_length = chromosome_lengthself.crossover_rate = crossover_rateself.mutation_rate = mutation_rateself.elitism_count = elitism_countself.bounds = bounds# 初始化种群self.population = self.initialize_population()self.best_individual = Noneself.best_fitness = float('-inf')self.fitness_history = []def initialize_population(self) -> np.ndarray:"""初始化种群 - 随机生成二进制编码的染色体"""return np.random.randint(0, 2, size=(self.population_size, self.chromosome_length))def decode_chromosome(self, chromosome: np.ndarray) -> float:"""将二进制染色体解码为实际数值"""# 将二进制转换为十进制decimal_value = int(''.join(map(str, chromosome)), 2)# 映射到指定范围min_bound, max_bound = self.boundsvalue = min_bound + decimal_value * (max_bound - min_bound) / (2**self.chromosome_length - 1)return valuedef calculate_fitness(self, chromosome: np.ndarray) -> float:"""计算适应度值"""x = self.decode_chromosome(chromosome)return self.objective_func(x)def select_parents(self, fitness_values: np.ndarray) -> List[np.ndarray]:"""轮盘赌选择父代"""# 确保适应度值为正min_fitness = np.min(fitness_values)if min_fitness < 0:fitness_values = fitness_values - min_fitness + 1e-6# 计算选择概率total_fitness = np.sum(fitness_values)probabilities = fitness_values / total_fitness# 选择父代selected_indices = np.random.choice(len(self.population), size=self.population_size - self.elitism_count, p=probabilities,replace=True)return [self.population[i] for i in selected_indices]def crossover(self, parent1: np.ndarray, parent2: np.ndarray) -> Tuple[np.ndarray, np.ndarray]:"""单点交叉"""if np.random.rand() < self.crossover_rate:# 随机选择交叉点crossover_point = np.random.randint(1, self.chromosome_length - 1)# 执行交叉child1 = np.concatenate([parent1[:crossover_point], parent2[crossover_point:]])child2 = np.concatenate([parent2[:crossover_point], parent1[crossover_point:]])return child1, child2else:return parent1.copy(), parent2.copy()def mutate(self, chromosome: np.ndarray) -> np.ndarray:"""位翻转变异"""mutated_chromosome = chromosome.copy()for i in range(len(mutated_chromosome)):if np.random.rand() < self.mutation_rate:mutated_chromosome[i] = 1 - mutated_chromosome[i] # 翻转位return mutated_chromosomedef evolve(self, generations: int = 100):"""执行进化过程"""for generation in range(generations):# 计算适应度fitness_values = np.array([self.calculate_fitness(ind) for ind in self.population])# 记录最佳个体best_idx = np.argmax(fitness_values)current_best_fitness = fitness_values[best_idx]if current_best_fitness > self.best_fitness:self.best_fitness = current_best_fitnessself.best_individual = self.population[best_idx].copy()self.fitness_history.append(self.best_fitness)# 选择精英elite_indices = np.argsort(fitness_values)[-self.elitism_count:]elites = [self.population[i] for i in elite_indices]# 选择父代parents = self.select_parents(fitness_values)# 交叉和变异产生新种群new_population = []# 添加精英new_population.extend(elites)# 生成后代for i in range(0, len(parents), 2):if i + 1 < len(parents):parent1, parent2 = parents[i], parents[i+1]child1, child2 = self.crossover(parent1, parent2)new_population.append(self.mutate(child1))new_population.append(self.mutate(child2))# 确保种群大小不变self.population = np.array(new_population[:self.population_size])# 打印进度if generation % 10 == 0:best_x = self.decode_chromosome(self.best_individual)print(f"Generation {generation}: Best Fitness = {self.best_fitness:.6f}, Best x = {best_x:.6f}")def get_best_solution(self) -> Tuple[float, float]:"""获取最佳解"""best_x = self.decode_chromosome(self.best_individual)return best_x, self.best_fitnessdef plot_progress(self):"""绘制进化过程"""plt.figure(figsize=(10, 6))plt.plot(self.fitness_history)plt.title('Evolution of Best Fitness')plt.xlabel('Generation')plt.ylabel('Fitness')plt.grid(True)plt.show()# 示例:寻找函数 f(x) = -x^2 + 10 的最大值
def objective_function(x):return -x**2 + 10# 运行遗传算法
if __name__ == "__main__":# 初始化遗传算法ga = GeneticAlgorithm(objective_func=objective_function,population_size=50,chromosome_length=20,crossover_rate=0.9,mutation_rate=0.01,elitism_count=2,bounds=(-10, 10))# 运行进化ga.evolve(generations=100)# 获取结果best_x, best_fitness = ga.get_best_solution()print(f"\n最佳解: x = {best_x:.6f}, f(x) = {best_fitness:.6f}")# 绘制进化过程ga.plot_progress()# 验证结果print(f"理论最大值在 x=0 处,f(0)=10")print(f"实际找到的最大值在 x={best_x:.6f} 处,f(x)={best_fitness:.6f}")更复杂的示例:多变量优化
# 多变量优化示例:寻找函数 f(x, y) = -x^2 - y^2 + 10 的最大值class MultiVariableGA:def __init__(self, objective_func: Callable,num_variables: int = 2,population_size: int = 100,chromosome_length_per_var: int = 10,crossover_rate: float = 0.8,mutation_rate: float = 0.01,elitism_count: int = 2,bounds: List[Tuple[float, float]] = [(-10, 10), (-10, 10)]):self.objective_func = objective_funcself.num_variables = num_variablesself.chromosome_length_per_var = chromosome_length_per_varself.total_chromosome_length = num_variables * chromosome_length_per_varself.bounds = boundsself.ga = GeneticAlgorithm(objective_func=self._evaluate,population_size=population_size,chromosome_length=self.total_chromosome_length,crossover_rate=crossover_rate,mutation_rate=mutation_rate,elitism_count=elitism_count,bounds=(0, 1) # 占位值,实际解码在_evaluate中处理)def _evaluate(self, chromosome: np.ndarray) -> float:"""解码染色体并评估适应度"""variables = []for i in range(self.num_variables):start_idx = i * self.chromosome_length_per_varend_idx = start_idx + self.chromosome_length_per_varvar_chromosome = chromosome[start_idx:end_idx]# 解码单个变量decimal_value = int(''.join(map(str, var_chromosome)), 2)min_bound, max_bound = self.bounds[i]value = min_bound + decimal_value * (max_bound - min_bound) / (2**self.chromosome_length_per_var - 1)variables.append(value)return self.objective_func(*variables)def evolve(self, generations: int = 100):"""执行进化"""self.ga.evolve(generations)def get_best_solution(self):"""获取最佳解"""best_chromosome = self.ga.best_individualvariables = []for i in range(self.num_variables):start_idx = i * self.chromosome_length_per_varend_idx = start_idx + self.chromosome_length_per_varvar_chromosome = best_chromosome[start_idx:end_idx]decimal_value = int(''.join(map(str, var_chromosome)), 2)min_bound, max_bound = self.bounds[i]value = min_bound + decimal_value * (max_bound - min_bound) / (2**self.chromosome_length_per_var - 1)variables.append(value)best_fitness = self.ga.best_fitnessreturn variables, best_fitness# 定义多变量目标函数
def multi_var_objective(x, y):return -x**2 - y**2 + 10# 运行多变量遗传算法
if __name__ == "__main__":multi_ga = MultiVariableGA(objective_func=multi_var_objective,num_variables=2,population_size=100,chromosome_length_per_var=15,crossover_rate=0.85,mutation_rate=0.02,bounds=[(-5, 5), (-5, 5)])multi_ga.evolve(generations=100)best_vars, best_fitness = multi_ga.get_best_solution()print(f"\n最佳解: x = {best_vars[0]:.6f}, y = {best_vars[1]:.6f}, f(x,y) = {best_fitness:.6f}")print(f"理论最大值在 (0,0) 处,f(0,0)=10")遗传算法的关键参数调优
种群大小:太小的种群可能无法充分探索搜索空间,太大的种群会增加计算成本
交叉率:控制交叉操作的概率,通常设置在0.6-0.9之间
变异率:通常设置较低的值(0.001-0.1),以避免破坏好的解
选择策略:除了轮盘赌选择,还可以使用锦标赛选择、排名选择等
编码方式:除了二进制编码,还可以使用实数编码、排列编码等
应用领域
遗传算法广泛应用于:
函数优化
机器学习参数调优
调度问题
路径规划
神经网络设计
图像处理
6.蚁群算法
蚁群算法(Ant Colony Optimization, ACO)是一种模拟蚂蚁觅食行为的群体智能优化算法。蚂蚁在寻找食物源时会释放信息素,其他蚂蚁能够感知这种信息素并倾向于跟随信息素浓度较高的路径,从而形成一种正反馈机制。
信息素:蚂蚁在路径上释放的化学物质,浓度越高表示路径越优
启发式信息:反映路径的直观吸引力(如距离的倒数)
状态转移规则:蚂蚁选择下一个节点的概率公式
信息素更新:包括挥发和增强两个过程
算法步骤
初始化参数和信息素矩阵
将蚂蚁放置在起始点
每只蚂蚁根据状态转移规则构建完整路径
计算每条路径的成本(如总距离)
更新信息素矩阵
重复步骤2-5直到满足终止条件
Python完整实现
下面以解决旅行商问题(TSP)为例实现蚁群算法:
import numpy as np
import matplotlib.pyplot as plt
import randomclass AntColonyOptimization:def __init__(self, distances, n_ants, n_best, n_iterations, decay, alpha=1, beta=1):"""初始化蚁群算法参数参数:distances: 城市间距离矩阵n_ants: 蚂蚁数量n_best: 每轮保留的最佳路径数量n_iterations: 迭代次数decay: 信息素挥发率alpha: 信息素重要程度参数beta: 启发式信息重要程度参数"""self.distances = distancesself.pheromone = np.ones(self.distances.shape) / len(distances)self.all_inds = range(len(distances))self.n_ants = n_antsself.n_best = n_bestself.n_iterations = n_iterationsself.decay = decayself.alpha = alphaself.beta = betadef run(self):"""运行蚁群算法"""best_path = Nonebest_distance = float('inf')best_paths = []best_distances = []for iteration in range(self.n_iterations):all_paths = self.gen_all_paths()self.spread_pheromone(all_paths, self.n_best)# 更新最佳路径shortest_path = min(all_paths, key=lambda x: x[1])if shortest_path[1] < best_distance:best_path = shortest_path[0]best_distance = shortest_path[1]best_paths.append(best_path)best_distances.append(best_distance)# 信息素挥发self.pheromone *= (1 - self.decay)if iteration % 10 == 0:print(f"迭代次数 {iteration}: 最佳距离 = {best_distance}")return best_path, best_distance, best_paths, best_distancesdef gen_path_dist(self, path):"""计算路径总距离"""total_dist = 0for i in range(len(path)):total_dist += self.distances[path[i-1]][path[i]]return total_distdef gen_all_paths(self):"""所有蚂蚁生成路径"""all_paths = []for _ in range(self.n_ants):path = self.gen_path(0) # 从城市0开始all_paths.append((path, self.gen_path_dist(path)))return all_pathsdef gen_path(self, start):"""单只蚂蚁生成路径"""path = [start]visited = set([start])while len(visited) < len(self.distances):probs = self.gen_move_probs(path[-1], visited)next_city = self.choose_next_city(probs)path.append(next_city)visited.add(next_city)return pathdef gen_move_probs(self, current, visited):"""生成移动到下一个城市的概率"""pheromone = np.copy(self.pheromone[current])pheromone[list(visited)] = 0 # 已访问城市概率设为0# 计算启发式信息(距离的倒数)heuristic = np.zeros(len(self.distances))for i in range(len(heuristic)):if i not in visited and self.distances[current][i] != 0:heuristic[i] = 1 / self.distances[current][i]# 计算概率分子numerator = (pheromone ** self.alpha) * (heuristic ** self.beta)# 归一化概率if np.sum(numerator) == 0:# 如果所有概率都为0,随机选择未访问城市unvisited = [i for i in self.all_inds if i not in visited]prob = np.zeros(len(self.distances))for city in unvisited:prob[city] = 1return prob / np.sum(prob)return numerator / np.sum(numerator)def choose_next_city(self, probs):"""根据概率选择下一个城市"""return np.random.choice(self.all_inds, 1, p=probs)[0]def spread_pheromone(self, all_paths, n_best):"""更新信息素"""# 按路径长度排序sorted_paths = sorted(all_paths, key=lambda x: x[1])# 只对最佳路径释放信息素for path, dist in sorted_paths[:n_best]:for i in range(len(path)):current_city = path[i]next_city = path[(i + 1) % len(path)]# 信息素增量与路径长度成反比self.pheromone[current_city][next_city] += 1 / distself.pheromone[next_city][current_city] += 1 / dist# 生成示例数据:随机城市坐标
def generate_cities(n_cities):np.random.seed(42)cities = np.random.rand(n_cities, 2) * 100return cities# 计算城市间距离矩阵
def calculate_distances(cities):n = len(cities)distances = np.zeros((n, n))for i in range(n):for j in range(n):if i != j:distances[i][j] = np.sqrt((cities[i][0] - cities[j][0])**2 + (cities[i][1] - cities[j][1])**2)return distances# 可视化结果
def plot_results(cities, best_path, best_distances):fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(15, 5))# 绘制最佳路径ax1.plot(cities[best_path, 0], cities[best_path, 1], 'o-')ax1.set_xlabel('X坐标')ax1.set_ylabel('Y坐标')ax1.set_title(f'最佳路径 (总距离: {best_distances[-1]:.2f})')# 绘制收敛曲线ax2.plot(best_distances)ax2.set_xlabel('迭代次数')ax2.set_ylabel('最短距离')ax2.set_title('收敛曲线')ax2.grid(True)plt.tight_layout()plt.show()# 主函数
def main():# 参数设置n_cities = 20n_ants = 30n_best = 5n_iterations = 100decay = 0.1alpha = 1beta = 2# 生成数据cities = generate_cities(n_cities)distances = calculate_distances(cities)# 运行蚁群算法aco = AntColonyOptimization(distances, n_ants, n_best, n_iterations, decay, alpha, beta)best_path, best_distance, best_paths, best_distances = aco.run()print(f"\n最终最佳路径: {best_path}")print(f"最终最短距离: {best_distance}")# 可视化结果plot_results(cities, best_path, best_distances)if __name__ == "__main__":main()蚂蚁数量:一般为城市数量的1-2倍
信息素挥发率(decay):0.1-0.5之间,避免过早收敛
α和β参数:
α控制信息素影响(通常1-2)
β控制启发式信息影响(通常2-5)
迭代次数:根据问题复杂度调整,通常100-1000次
算法优缺点
优点:
强大的全局搜索能力
正反馈机制促进优良解的发现
易于并行化处理
适用于离散优化问题
缺点:
收敛速度较慢
参数调节复杂
容易陷入局部最优(需配合局部搜索)
应用领域
旅行商问题(TSP)
车辆路径问题(VRP)
作业车间调度
网络路由优化
数据挖掘中的聚类分析
7.ARIMA模型
ARIMA(Autoregressive Integrated Moving Average),全称为自回归积分滑动平均模型。它是时间序列预测中最经典、最常用的方法之一,尤其适用于处理非平稳序列。
1. 核心思想
ARIMA模型的核心思想是:将非平稳时间序列转化为平稳时间序列,然后将因变量仅对其滞后值以及随机误差项的现值和滞后值进行回归所建立的模型。
2. 模型结构:ARIMA(p, d, q)
模型由三个部分组成,对应三个参数 (p, d, q):
AR(p) - 自回归部分 (Autoregressive)
含义:描述当前值与历史值之间的关系。用变量自身的历史时间数据来预测自己。
模型:$X_t = c + \sum_{i=1}^{p} \phi_i X_{t-i} + \epsilon_t$
参数
p:自回归项的阶数,表示用过去多少期的数据来预测当前值。可以通过偏自相关函数(PACF) 图来确定。
I(d) - 差分部分 (Integrated)
含义:将非平稳时间序列转换为平稳序列的过程。差分可以消除数据中的趋势和季节性。
操作:d阶差分就是计算d次相邻观测值之间的差值。
1阶差分:$X’t = X_t - X{t-1}$
2阶差分:$X’’t = X’t - X’{t-1} = (X_t - X{t-1}) - (X_{t-1} - X_{t-2})$
参数
d:使序列变为平稳所需的最小差分阶数。通常通过ADF检验(单位根检验) 来确定。
MA(q) - 移动平均部分 (Moving Average)
含义:描述当前值与历史预测误差之间的关系。它捕捉的是时间序列中随机冲击的效应。
模型:$X_t = \mu + \epsilon_t + \sum_{i=1}^{q} \theta_i \epsilon_{t-i}$
参数
q:移动平均项的阶数,表示模型使用过去多少个预测误差。可以通过自相关函数(ACF) 图来确定。
综合模型ARIMA(p, d, q):
对原始序列进行d阶差分后,得到的新序列遵循ARMA(p, q)模型。
$\Delta^d X_t = c + \sum_{i=1}^{p} \phi_i \Delta^d X_{t-i} + \epsilon_t + \sum_{i=1}^{q} \theta_i \epsilon_{t-i}$
其中,$\Delta^d$ 是d阶差分算子。
3. 建模步骤
序列平稳化 (确定d)
绘制原始序列图,观察是否有明显趋势或季节性。
进行ADF单位根检验。如果p-value > 0.05,则认为序列不平稳,需要进行差分。
重复差分和ADF检验,直到序列平稳,记录差分次数
d。
确定p和q
对平稳化后的序列绘制ACF(自相关图) 和PACF(偏自相关图)。
ACF图:拖尾(逐渐衰减到0)还是截尾(快速降为0)。
PACF图:拖尾还是截尾。
粗略判断准则:
p的确定:看PACF图。如果PACF在滞后p阶后截尾(突然趋于0),则p可以取该值。
q的确定:看ACF图。如果ACF在滞后q阶后截尾,则q可以取该值。
更精确的方法是使用网格搜索(Grid Search),根据AIC(Akaike Information Criterion) 或BIC(Bayesian Information Criterion) 准则来选择模型,AIC/BIC越小越好。
参数估计
使用最大似然估计(MLE)等方法来确定AR和MA项的系数 ($\phi_i$, $\theta_i$)。
模型诊断
残差分析:一个好的ARIMA模型的残差应该是一个白噪声(均值为0,方差恒定,无自相关)。
绘制残差图,观察是否在0附近随机波动。
对残差进行Ljung-Box检验,如果p-value很大(>0.05),则不能拒绝残差是白噪声的原假设,说明模型拟合良好。
预测
使用拟合好的模型进行未来值的预测。
4.Python
我们将使用经典的AirPassengers(航空公司乘客)数据集来演示。
1. 导入必要库
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline# 统计模型
from statsmodels.tsa.stattools import adfuller # ADF检验
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf # ACF/PACF图
from statsmodels.tsa.arima.model import ARIMA # ARIMA模型# 评估指标
from sklearn.metrics import mean_squared_error, mean_absolute_error
import warnings
warnings.filterwarnings('ignore') # 忽略警告信息2. 加载数据并探索
# 加载数据
url = "https://raw.githubusercontent.com/jbrownlee/Datasets/master/airline-passengers.csv"
data = pd.read_csv(url, parse_dates=['Month'], index_col='Month')
data.index.freq = 'MS' # 设置频率为“月起始”(Month Start)
series = data['Passengers']# 查看数据
print(series.head())
plt.figure(figsize=(12, 5))
plt.plot(series)
plt.title('AirPassengers Dataset')
plt.xlabel('Year')
plt.ylabel('Passengers')
plt.grid(True)
plt.show()3. 序列平稳化 - 确定参数d
# 定义ADF检验函数
def adf_test(series):result = adfuller(series)print('ADF Statistic: %f' % result[0])print('p-value: %f' % result[1])print('Critical Values:')for key, value in result[4].items():print('\t%s: %.3f' % (key, value))if result[1] <= 0.05:print("-> p-value <= 0.05. Reject the null hypothesis. Data is stationary.")else:print("-> p-value > 0.05. Fail to reject the null hypothesis. Data is non-stationary.")# 对原始序列进行ADF检验
print("ADF Test for Original Series:")
adf_test(series)# 进行1阶差分并再次检验
series_diff_1 = series.diff().dropna()
print("\nADF Test after 1st Order Differencing:")
adf_test(series_diff_1)# 绘制差分后的序列
plt.figure(figsize=(12, 5))
plt.plot(series_diff_1)
plt.title('AirPassengers After 1st Order Differencing')
plt.grid(True)
plt.show()输出:原始序列p值很大,非平稳。1阶差分后p值可能仍然>0.05(因为还有季节性),但对于演示,我们通常取d=1。对于有强季节性的数据,需要使用SARIMA(季节性ARIMA),但这里我们先按简单ARIMA处理,取d=1。
4. 确定参数p和q
# 对平稳化后的序列(差分后)绘制ACF和PACF图
fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(12, 8))# ACF图
plot_acf(series_diff_1, lags=40, ax=ax1)
ax1.set_title('Autocorrelation Function (ACF)')# PACF图
plot_pacf(series_diff_1, lags=40, ax=ax2, method='ywm') # 使用 ywm 方法避免警告
ax2.set_title('Partial Autocorrelation Function (PACF)')plt.tight_layout()
plt.show()更严谨的方法是使用网格搜索确定p和q:
# 网格搜索寻找最佳p, q组合 (d已固定为1)
# 定义p, d, q参数的取值范围
p_range = range(0, 4) # 0 to 3
q_range = range(0, 4) # 0 to 3
d = 1best_aic = np.inf
best_order = Nonefor p in p_range:for q in q_range:try:model = ARIMA(series, order=(p, d, q))results = model.fit()aic = results.aicif aic < best_aic:best_aic = aicbest_order = (p, d, q)print(f'ARIMA({p},{d},{q}) - AIC: {aic:.2f}')except Exception as e:print(f'Error fitting ARIMA({p},{d},{q}): {e}')continueprint(f'\nBest Model Order: ARIMA{best_order} with AIC: {best_aic:.2f}')5. 拟合ARIMA模型
# 使用确定的参数 (p,d,q) 拟合模型
# 这里我们使用 (2, 1, 1),请根据你的网格搜索结果修改
p, d, q = 2, 1, 1model = ARIMA(series, order=(p, d, q))
model_fit = model.fit()# 输出模型摘要
print(model_fit.summary())6. 模型诊断 - 残差分析
# 绘制残差图
residuals = model_fit.resid
plt.figure(figsize=(12, 5))
plt.plot(residuals)
plt.title('Residuals from ARIMA Model')
plt.grid(True)
plt.show()# 残差的ACF图
plot_acf(residuals, lags=40)
plt.title('ACF of Residuals')
plt.show()# Ljung-Box检验 (查看残差是否为白噪声)
from statsmodels.stats.diagnostic import acorr_ljungbox
lb_test = acorr_ljungbox(residuals, lags=10, return_df=True)
print("Ljung-Box test results for residuals:")
print(lb_test)# 如果所有p-value都很大(>0.05),说明残差是白噪声,模型OK7. 预测
# 划分训练集和测试集 (最后24个月作为测试集)
split_point = len(series) - 24
train, test = series.iloc[:split_point], series.iloc[split_point:]# 在训练集上重新拟合模型
model_train = ARIMA(train, order=(p, d, q))
model_train_fit = model_train.fit()# 进行预测
# start: 预测开始的索引
# end: 预测结束的索引
# dynamic: False 表示使用一步预测(更准确但可能滞后)
forecast = model_train_fit.get_prediction(start=len(train), end=len(series)-1, dynamic=False)
forecast_values = forecast.predicted_mean
forecast_ci = forecast.conf_int() # 置信区间# 计算评估指标
mse = mean_squared_error(test, forecast_values)
rmse = np.sqrt(mse)
mae = mean_absolute_error(test, forecast_values)
print(f'\nTest MSE: {mse:.2f}')
print(f'Test RMSE: {rmse:.2f}')
print(f'Test MAE: {mae:.2f}')# 绘制结果
plt.figure(figsize=(14, 7))
plt.plot(train, label='Training Data')
plt.plot(test, label='Actual Test Data', color='blue')
plt.plot(forecast_values, color='red', label='Forecast')
# 绘制置信区间
plt.fill_between(forecast_ci.index,forecast_ci.iloc[:, 0],forecast_ci.iloc[:, 1], color='pink', alpha=0.3, label='95% Confidence Interval')
plt.title('ARIMA Model Forecast vs Actuals')
plt.legend()
plt.grid(True)
plt.show()8. 预测未来(未知)数据
# 使用全部数据重新拟合最终模型
final_model = ARIMA(series, order=(p, d, q))
final_model_fit = final_model.fit()# 预测未来12个月
forecast_steps = 12
forecast_future = final_model_fit.get_forecast(steps=forecast_steps)
forecast_future_values = forecast_future.predicted_mean
forecast_future_ci = forecast_future.conf_int()# 创建未来时间的索引
future_index = pd.date_range(series.index[-1] + pd.DateOffset(months=1), periods=forecast_steps, freq='MS')# 绘制历史数据和未来预测
plt.figure(figsize=(14, 7))
plt.plot(series, label='Historical Data')
plt.plot(future_index, forecast_future_values, color='green', label='Future Forecast')
plt.fill_between(future_index,forecast_future_ci.iloc[:, 0],forecast_future_ci.iloc[:, 1], color='lightgreen', alpha=0.3, label='95% Confidence Interval')
plt.title(f'ARIMA{best_order} Forecast for Next {forecast_steps} Months')
plt.legend()
plt.grid(True)
plt.show()# 打印预测值
print("\nFuture Forecast Values:")
print(pd.DataFrame({'Date': future_index, 'Forecasted_Passengers': forecast_future_values.values}).round(1))