【LeetCode每日一题】160.相交链表 206. 反转链表
每日一题
- 160.相交链表
- 题目
- 总体思路
- 算法原理
- 数学证明
- 代码
- go语言链表实现
- 206. 反转链表
- 题目
- 总体思路
- 迭代法
- 算法原理
- 时间复杂度与空间复杂度
- 递归法
- 递归思路
- 时间复杂度与空间复杂度
- 代码
- 迭代法
- 递归法
2025.8.28
160.相交链表
题目
给你两个单链表的头节点 headA 和 headB ,请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点,返回 null 。
图示两个链表在节点 c1 开始相交:
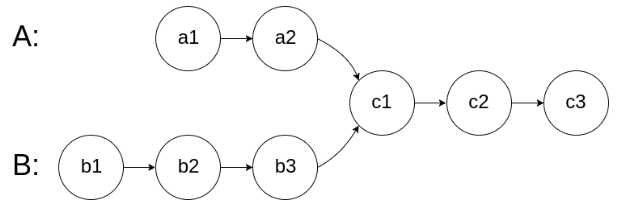
题目数据 保证 整个链式结构中不存在环。
注意,函数返回结果后,链表必须 保持其原始结构 。
自定义评测:
评测系统 的输入如下(你设计的程序 不适用 此输入):
intersectVal - 相交的起始节点的值。如果不存在相交节点,这一值为 0
listA - 第一个链表
listB - 第二个链表
skipA - 在 listA 中(从头节点开始)跳到交叉节点的节点数
skipB - 在 listB 中(从头节点开始)跳到交叉节点的节点数
评测系统将根据这些输入创建链式数据结构,并将两个头节点 headA 和 headB 传递给你的程序。如果程序能够正确返回相交节点,那么你的解决方案将被 视作正确答案 。
示例 1:
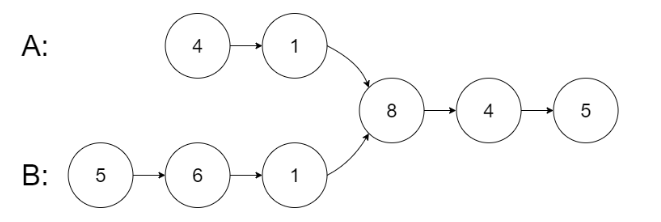
输入:intersectVal = 8, listA = [4,1,8,4,5], listB = [5,6,1,8,4,5], skipA = 2, skipB = 3
输出:Intersected at ‘8’
解释:相交节点的值为 8 (注意,如果两个链表相交则不能为 0)。
从各自的表头开始算起,链表 A 为 [4,1,8,4,5],链表 B 为 [5,6,1,8,4,5]。
在 A 中,相交节点前有 2 个节点;在 B 中,相交节点前有 3 个节点。
— 请注意相交节点的值不为 1,因为在链表 A 和链表 B 之中值为 1 的节点 (A 中第二个节点和 B 中第三个节点) 是不同的节点。换句话说,它们在内存中指向两个不同的位置,而链表 A 和链表 B 中值为 8 的节点 (A 中第三个节点,B 中第四个节点) 在内存中指向相同的位置。
示例 2:
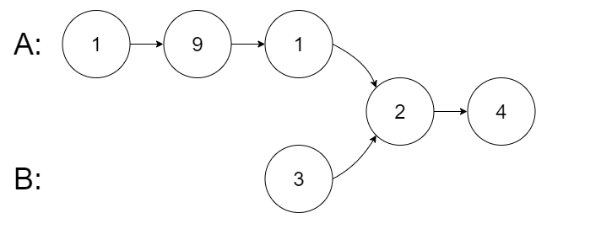
输入:intersectVal = 2, listA = [1,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1
输出:Intersected at ‘2’
解释:相交节点的值为 2 (注意,如果两个链表相交则不能为 0)。
从各自的表头开始算起,链表 A 为 [1,9,1,2,4],链表 B 为 [3,2,4]。
在 A 中,相交节点前有 3 个节点;在 B 中,相交节点前有 1 个节点。
示例 3:
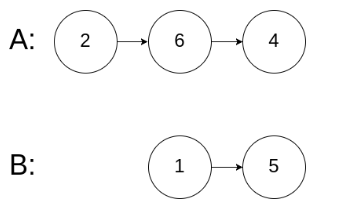
输入:intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2
输出:No intersection
解释:从各自的表头开始算起,链表 A 为 [2,6,4],链表 B 为 [1,5]。
由于这两个链表不相交,所以 intersectVal 必须为 0,而 skipA 和 skipB 可以是任意值。
这两个链表不相交,因此返回 null 。
提示:
listA 中节点数目为 m
listB 中节点数目为 n
1 <= m, n <= 3 * 104
1 <= Node.val <= 105
0 <= skipA <= m
0 <= skipB <= n
如果 listA 和 listB 没有交点,intersectVal 为 0
如果 listA 和 listB 有交点,intersectVal == listA[skipA] == listB[skipB]
进阶:你能否设计一个时间复杂度 O(m + n) 、仅用 O(1) 内存的解决方案?
总体思路
算法原理
使用双指针技巧来查找两个链表的相交节点:
-
指针初始化:两个指针分别指向两个链表的头节点
-
同步遍历:两个指针同时向前移动
-
链表切换:当某个指针到达链表末尾时,切换到另一个链表的头部
-
相遇判断:两个指针最终会在相交节点相遇,或者同时到达nil(表示没有相交)
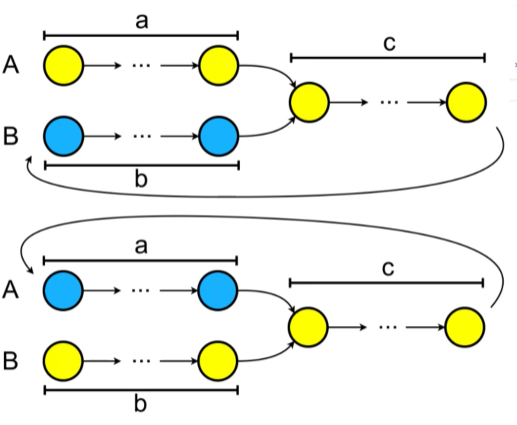
数学证明
假设:
-
链表A长度为a+c,独立部分长度为a
-
链表B长度为b+c,独立部分长度为b
-
相交部分长度为c
那么两个指针走过的路径长度都是:a + b + c
因此它们会在相交节点相遇。
-
时间复杂度:
O(m + n)-
最坏情况下需要遍历两个链表各一次
-
m 和 n 分别是两个链表的长度
-
-
空间复杂度:
O(1)-
只使用两个指针变量
-
不需要额外数据结构
-
代码
golang
/*** Definition for singly-linked list.* type ListNode struct {* Val int* Next *ListNode* }*/
func getIntersectionNode(headA, headB *ListNode) *ListNode {// 边界条件检查:如果任一链表为空,直接返回nilif headA == nil || headB == nil {return nil}// 初始化两个指针,分别指向两个链表的头节点tempA := headAtempB := headB// 循环直到两个指针相遇(找到相交节点)或都为nil(没有相交)for tempA != tempB {// 指针A移动:如果还没到链表末尾,继续向前移动if tempA != nil {tempA = tempA.Next} else {// 指针A到达链表A末尾,切换到链表B的头部继续遍历tempA = headB}// 指针B移动:如果还没到链表末尾,继续向前移动if tempB != nil {tempB = tempB.Next} else {// 指针B到达链表B末尾,切换到链表A的头部继续遍历tempB = headA}}// 返回相遇的节点(如果没相交,tempA和tempB会同时为nil)return tempA
}
func getIntersectionNode(headA, headB *ListNode) *ListNode {if headA == nil || headB == nil {return nil}A := headAB := headBfor A != B {if A != nil {A = A.Next}else{A = headB}if B != nil {B = B.Next}else{B = headA}}return A
}
go语言链表实现
- 自定义链表实现
定义链表节点
type ListNode struct {Val int // 节点值Next *ListNode // 指向下一个节点的指针
}
创建链表
// 创建空链表
var head *ListNode = nil// 创建包含元素的链表
func createList(values []int) *ListNode {if len(values) == 0 {return nil}head := &ListNode{Val: values[0]}current := headfor i := 1; i < len(values); i++ {current.Next = &ListNode{Val: values[i]}current = current.Next}return head
}
- 标准库中的链表
Go标准库提供了container/list包来实现双向链表:
import "container/list"// 创建链表
l := list.New()// 添加元素
l.PushBack(1) // 在尾部添加
l.PushFront(2) // 在头部添加// 遍历链表
for e := l.Front(); e != nil; e = e.Next() {fmt.Println(e.Value)
}
206. 反转链表
题目
给你单链表的头节点 head ,请你反转链表,并返回反转后的链表。
示例 1:
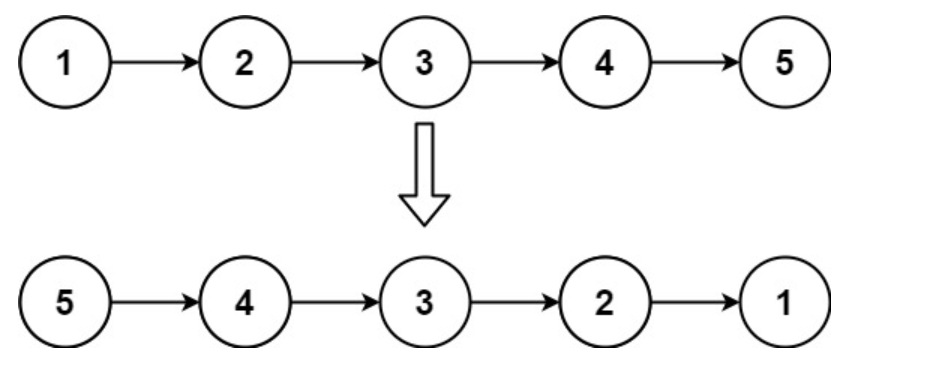
输入:head = [1,2,3,4,5]
输出:[5,4,3,2,1]
示例 2:
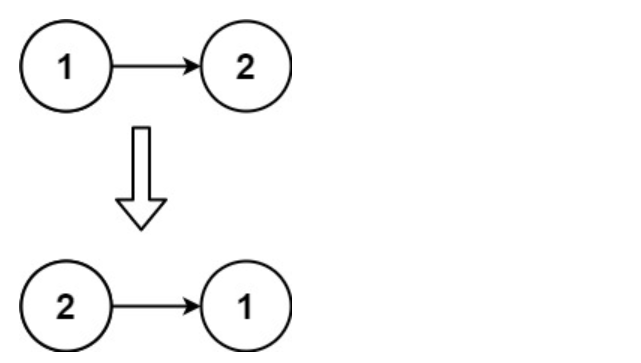
输入:head = [1,2]
输出:[2,1]
示例 3:
输入:head = []
输出:[]
提示:
链表中节点的数目范围是 [0, 5000]
-5000 <= Node.val <= 5000
进阶:链表可以选用迭代或递归方式完成反转。你能否用两种方法解决这道题?
总体思路
迭代法
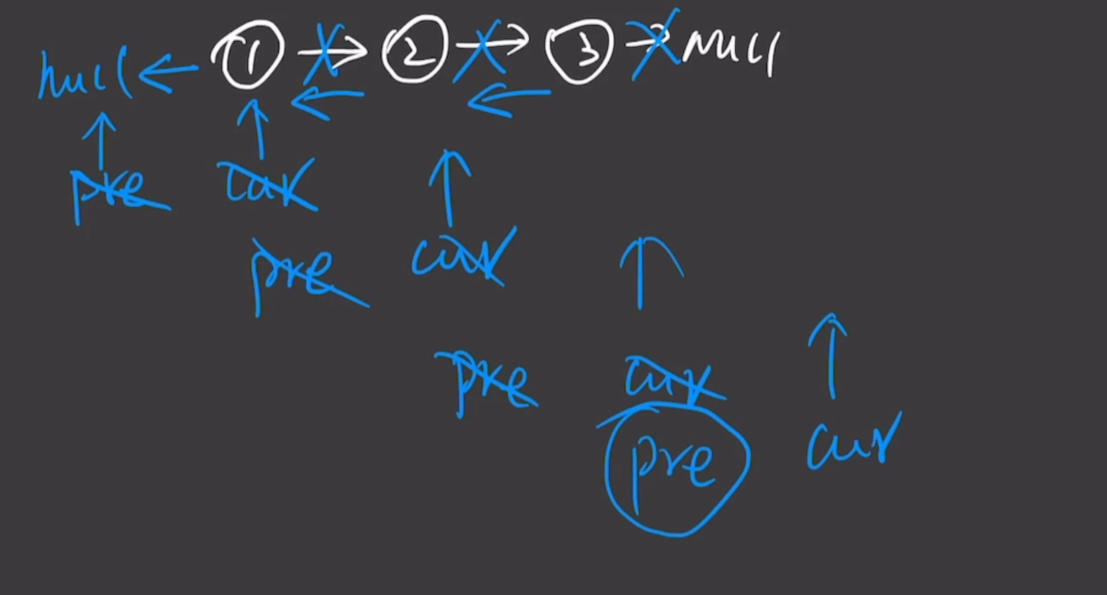
采用迭代法来反转单链表。核心思想是使用三个指针(前驱、当前、临时)来遍历链表,在遍历过程中逐个反转节点的指向,最终将整个链表的连接方向完全反转。
算法原理
- 三指针协同:使用pre、cur、tmp三个指针协同工作
- 逐步反转:每次处理一个节点,将其指向前一个节点
- 指针前进:处理完后指针向前移动,继续处理下一个节点
- 头尾转换:原来的头节点变成尾节点,原来的尾节点变成新的头节点
时间复杂度与空间复杂度
- 时间复杂度:O(n)
- 只需要遍历链表一次
- n为链表的节点数量
- 空间复杂度:O(1)
- 只使用了3个指针变量
- 不需要额外的数据结构
递归法
递归思路
- 分解问题:将大问题分解为小问题
- 递归反转:先反转剩余部分链表
- 处理当前:将当前节点连接到已反转链表的尾部
- 终止条件:空链表或单节点链表直接返回
时间复杂度与空间复杂度
- 时间复杂度:O(n)
- 需要递归n次(链表长度)
- 每次递归操作是常数时间
- 空间复杂度:O(n)
- 递归调用栈的深度为n
- 最坏情况下需要n层递归栈
代码
golang
迭代法
/*** 反转单链表* @param head *ListNode 链表的头节点* @return *ListNode 反转后链表的头节点*/
func reverseList(head *ListNode) *ListNode {// 边界条件检查:如果链表为空,直接返回nil// 这是防御性编程的重要部分,避免空指针异常if head == nil {return head}// 初始化指针:// pre - 前驱节点指针,初始为nil(表示还没有前驱节点)// cur - 当前节点指针,从头节点开始遍历var pre *ListNode = nilcur := head// 主循环:遍历链表直到当前节点为nil(链表末尾)// 每次循环处理一个节点的指针反转for cur != nil {// 保存当前节点的下一个节点到临时变量tmp// 这是关键步骤:因为下一步要修改cur.Next,需要先保存下一个节点的引用tmp := cur.Next// 反转指针:将当前节点的Next指向前驱节点// 这是实际的反转操作,改变节点的指向cur.Next = pre// 移动前驱指针:前驱指针前进到当前节点位置// 当前节点已经成为下一个节点的前驱节点pre = cur// 移动当前指针:当前指针前进到之前保存的下一个节点// 使用tmp而不是cur.Next是因为cur.Next已经被修改了cur = tmp}// 循环结束后,pre指向原链表的最后一个节点,即新链表的头节点// cur为nil,表示已经处理完所有节点return pre
}
/*** Definition for singly-linked list.* type ListNode struct {* Val int* Next *ListNode* }*/
func reverseList(head *ListNode) *ListNode {if head == nil {return head}var pre *ListNode = nilcur := headfor cur != nil {tmp := cur.Nextcur.Next = prepre = curcur = tmp}return pre
}
递归法
/*** Definition for singly-linked list.* type ListNode struct {* Val int* Next *ListNode* }*/
func reverseList(head *ListNode) *ListNode {// 递归终止条件:空链表或单节点链表if head == nil || head.Next == nil {return head}// 递归反转剩余部分链表newHead := reverseList(head.Next)// 将当前节点的下一个节点指向当前节点(反转指针)head.Next.Next = head// 将当前节点的Next设为nil(避免循环)head.Next = nil// 返回新的头节点return newHead
}
