深度学习③【卷积神经网络(CNN)详解:从卷积核到特征提取的视觉革命(概念篇)】
文章目录
- 先言
- 1. 卷积核:特征检测的魔法窗口
- 1.1什么是卷积核:可学习的特征检测器
- 1.2可视化理解:边缘检测、纹理提取、特征发现
- 1.3代码实现:使用PyTorch定义和初始化卷积层
- 2. 卷积运算的数学原理
- 2.1.离散卷积计算:滑动窗口的点乘求和
- 2.2.步长(Stride):控制输出尺寸和计算效率
- 3.3.填充(Padding):保持空间分辨率的技巧
- 3.4.深度维度:多通道多卷积核输入输出的处理机制
- 3.5空间可分离卷积运算
- 3.6深度(通道)可分离卷积
- 3.池化层:智能降维与空间不变性
- 3.1.最大池化(Max Pooling):保留最显著特征
- 3.2.平均池化(Average Pooling):平滑特征响应
- 3.3池化的作用:减少参数、控制过拟合、提供平移不变性
- 4.感受野:从像素到非线性概念的映射
- 4.1感受野定义:输出特征图中的每个单元对应输入图像的区域大小
- 4.2设计意义:如何设计网络结构来获得适当的感受野
- 结语
先言
在深度学习领域,卷积神经网络(CNN) 彻底改变了计算机视觉的发展进程。从人脸识别到自动驾驶,从医疗影像到卫星图像分析,CNN凭借其独特的局部连接、权重共享和层次化特征提取机制,成为处理图像数据的首选架构。
本文将深入解析CNN的核心组件:
✅ 卷积核(Kernel):特征提取的"显微镜"
✅ 卷积运算:参数共享的高效计算
✅ 特征提取:从边缘到语义的层次化学习
✅ 池化(Pooling):降维与平移不变性的关键
✅ 感受野(Receptive Field):理解像素到概念的映射过程
无论你是计算机视觉初学者,还是希望深入理解CNN工作原理的开发者,这篇文章都将为你揭示卷积神经网络背后的数学原理和设计哲学!
1. 卷积核:特征检测的魔法窗口
示例:pandas 是基于NumPy 的一种工具,该工具是为了解决数据分析任务而创建的。
1.1什么是卷积核:可学习的特征检测器
卷积核是卷积运算过程中必不可少的一个“工具”,在卷积神经网络中,卷积核是非常重要的,它们被用来提取图像中的特征。
卷积核其实是一个小矩阵,在定义时需要考虑以下几方面的内容:
- 卷积核的个数:卷积核(过滤器)的个数决定了其输出特征矩阵的通道数。
- 卷积核的值:卷积核的值是初始化好的,后续进行更新。
- 卷积核的大小:常见的卷积核有1×1、3×3、5×5等,一般都是奇数 × 奇数。
下图就是一个3×3的卷积核:

1.2可视化理解:边缘检测、纹理提取、特征发现

与传统网络区别:
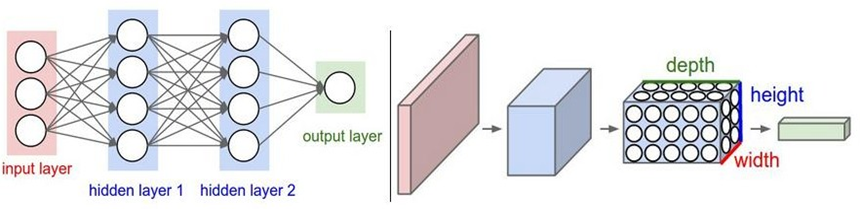
全连接神经网络的角色只是一个分类器,如果将整个图片直接输入网络,不仅参数量大,也没有利用好图片中像素的空间特性,增加了学习难度,降低了学习效果。
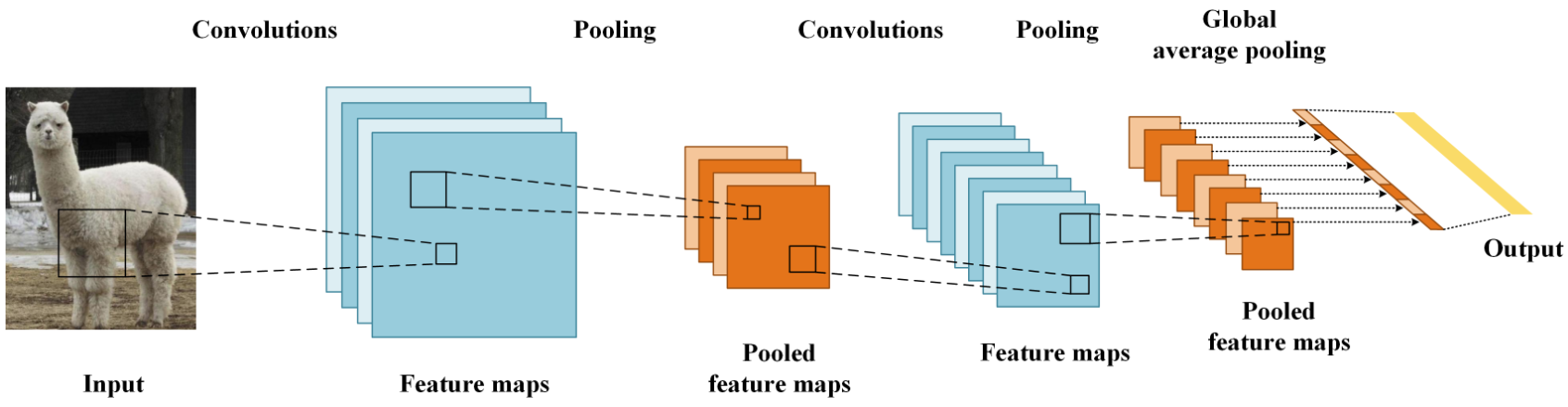
卷积和通过卷积核运算对图像特征进行提取保留了图像的空间特性,并且多通道的卷积还可以有效保留图像的颜色特征,从而实现对图像的边缘检测、纹理提取、颜色特征发现等高效操作。
1.3代码实现:使用PyTorch定义和初始化卷积层
import torch
import torch.nn as nn
import os
import matplotlib.pyplot as plt
def test01():data_base =os.path.dirname(__file__)data_path = os.path.join(data_base,'data','彩色.png')image = plt.imread(data_path)print(image.shape)#对图片数据进行升维变化 hwc->NCHW 并且变为张量image = torch.tensor(image.transpose(2,0,1)).unsqueeze(0)print(image.shape)conv = nn.Conv2d(in_channels=4,#输入的特征数,通道数out_channels=3,#输出的特征数,通道数kernel_size=3,#卷积核大小stride=1,#步长# padding=1#填充)#调用单层卷积神经out_img = conv(image)print(out_img.shape)#N C H W ->C H W ->H W Cout_img=out_img.squeeze(0).detach().numpy().transpose(1,2,0)plt.imshow(out_img)plt.show()
test01()
2. 卷积运算的数学原理
2.1.离散卷积计算:滑动窗口的点乘求和
卷积的过程是将卷积核在图像上进行滑动计算,每次滑动到一个新的位置时,卷积核和图像进行点对点的计算,并将其求和得到一个新的值,然后将这个新的值加入到特征图中,最终得到一个新的特征图。
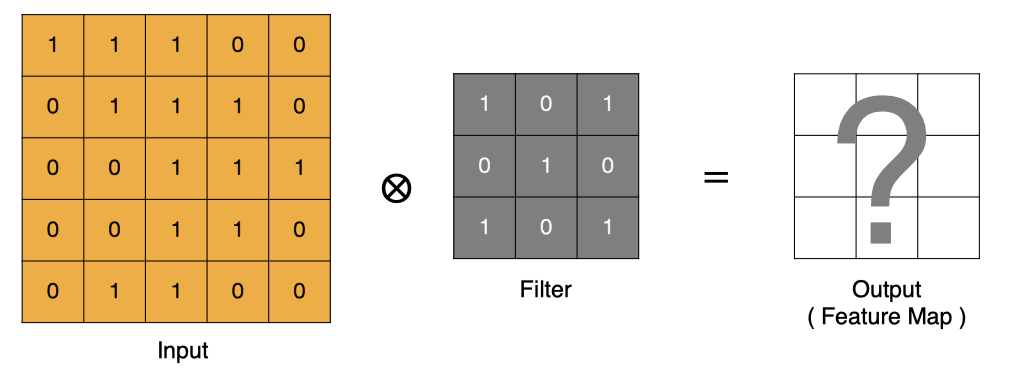
- input 表示输入的图像
- filter 表示卷积核, 也叫做滤波器
- input 经过 filter 的得到输出为最右侧的图像,该图叫做特征图
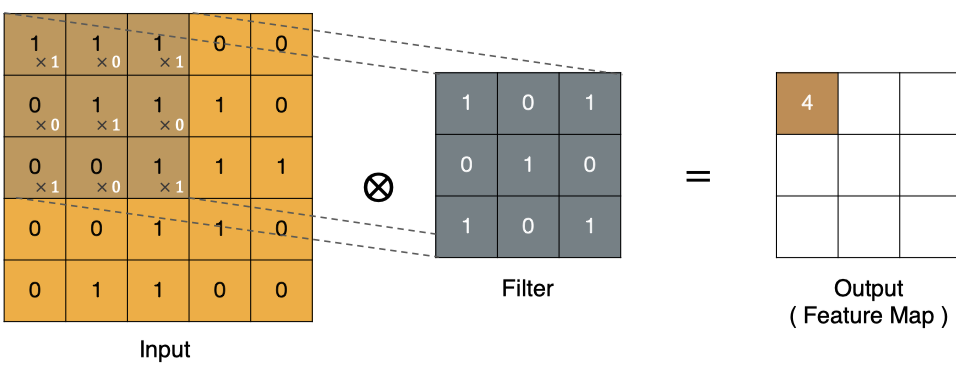
计算方式:
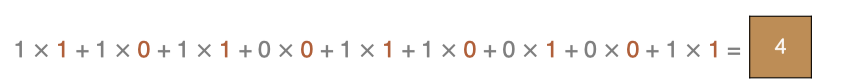
最终特征图:
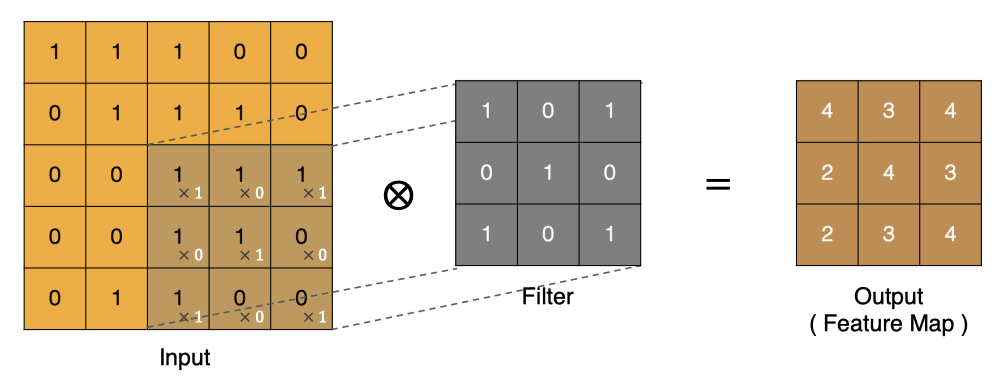
卷积的重要性在于它可以将图像中的特征与卷积核进行卷积操作,从而提取出图像中的特征。
可以通过不断调整卷积核的大小、卷积核的值和卷积操作的步长,可以提取出不同尺度和位置的特征。
2.2.步长(Stride):控制输出尺寸和计算效率
按照步长为1来移动卷积核,计算特征图如下所示:

如果我们把 Stride 增大为2,也是可以提取特征图的,如下图所示:

stride太小:重复计算较多,计算量大,训练效率降低;
stride太大:会造成信息遗漏,无法有效提炼数据背后的特征;
3.3.填充(Padding):保持空间分辨率的技巧
Padding
通过上面的卷积计算,我们发现最终的特征图比原始图像要小,如果想要保持图像大小不变, 可在原图周围添加padding来实现。
更重要的,边缘填充还更好的保护了图像边缘数据的特征。
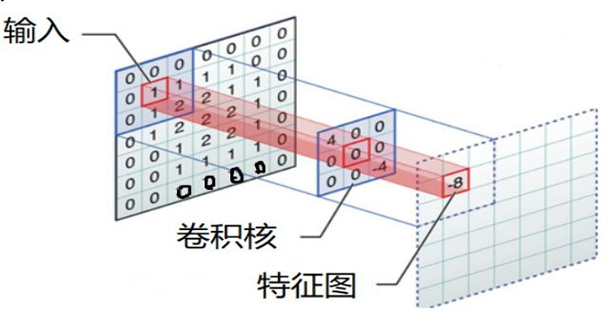
3.4.深度维度:多通道多卷积核输入输出的处理机制
深度多通道卷积运算视图:
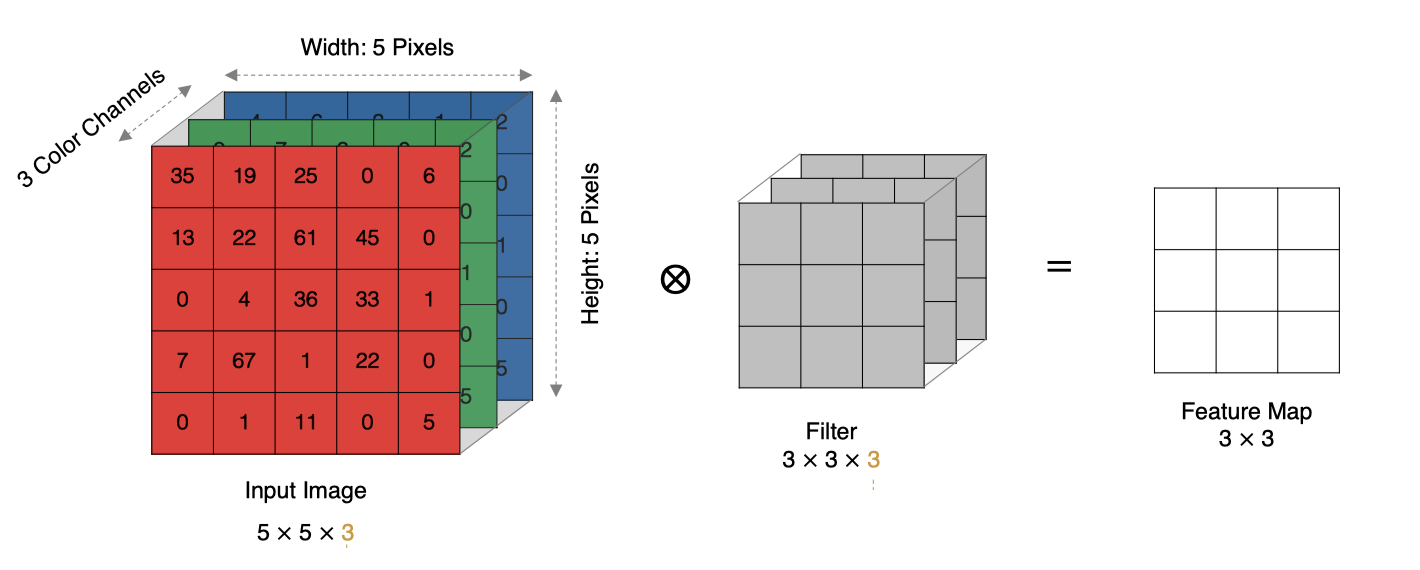
计算方法:
- 当输入有多个通道(Channel), 例如RGB三通道, 此时要求卷积核需要有相同的通道数。
- 卷积核通道与对应的输入图像通道进行卷积。
- 将每个通道的卷积结果按位相加得到最终的特征图。
计算示意图:
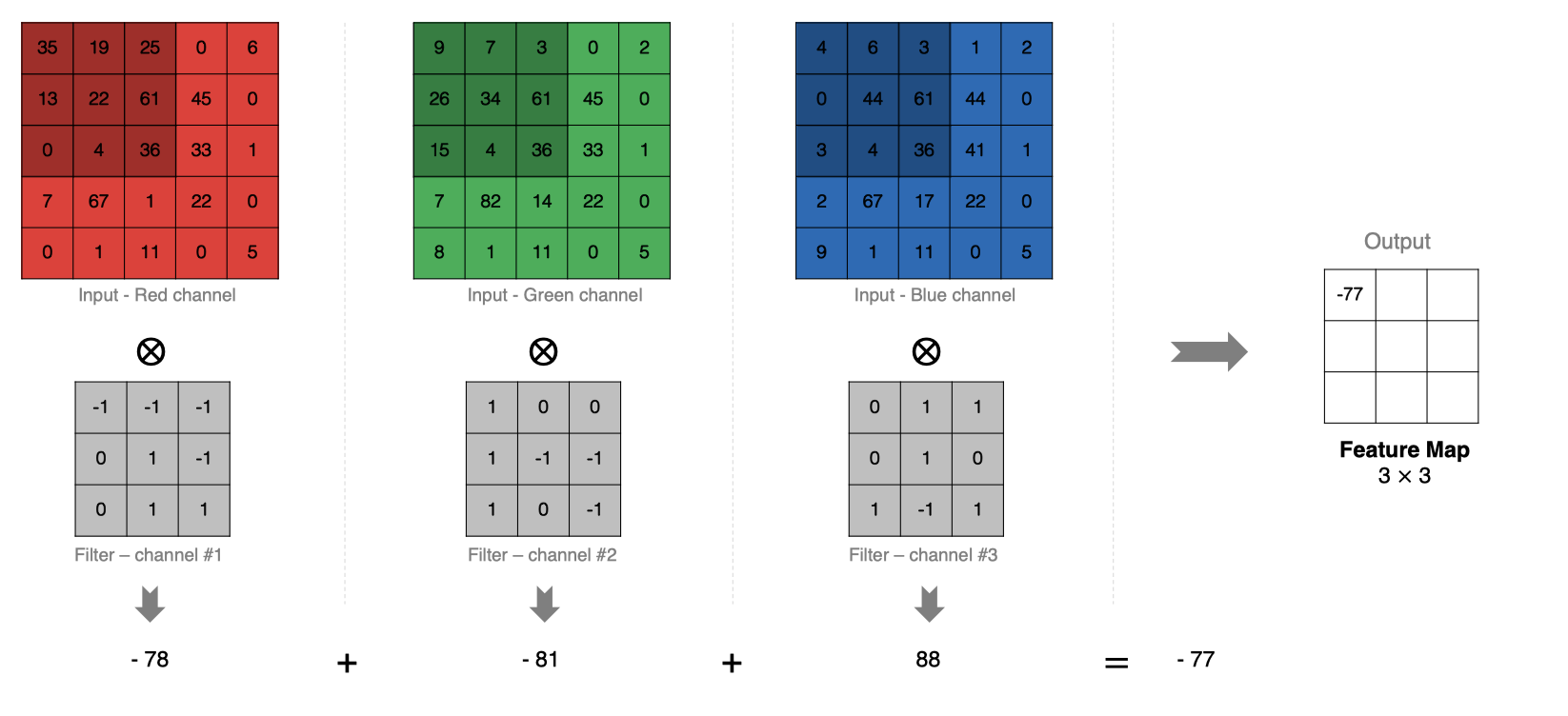
维度多卷积运算视图:
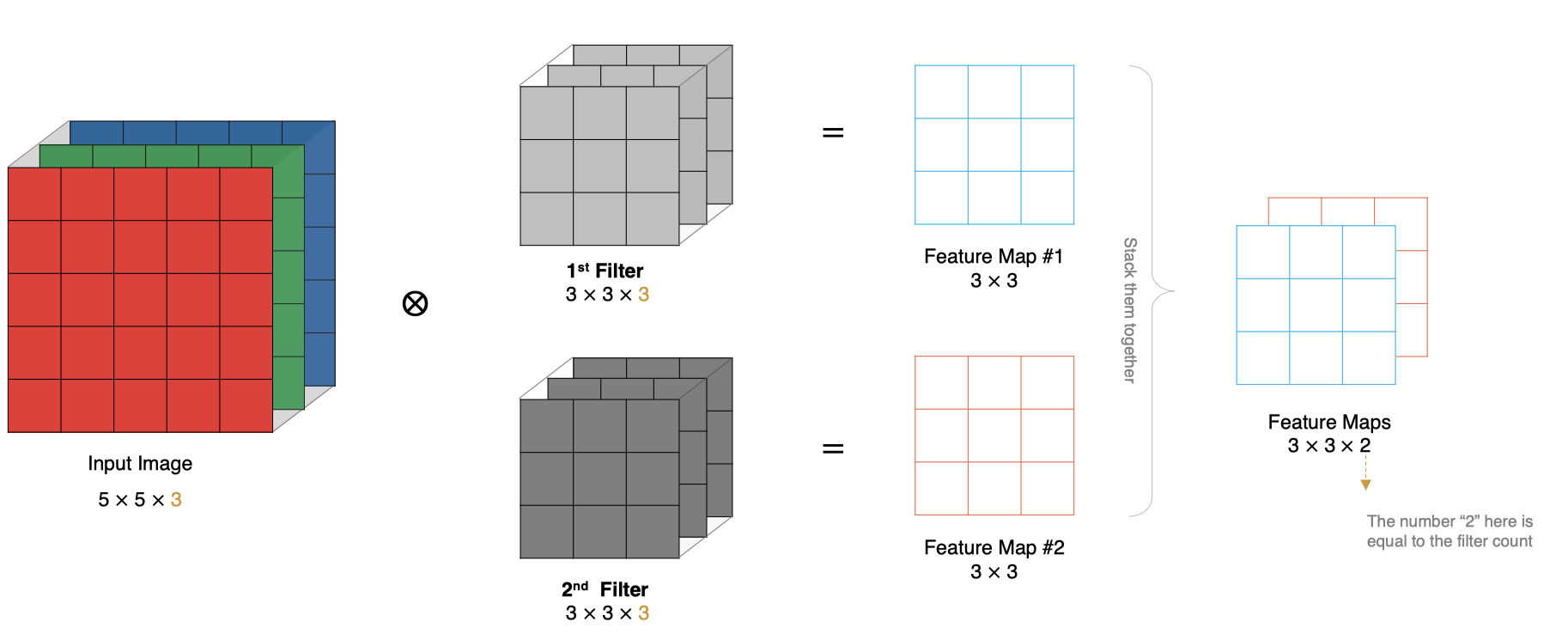
3.5空间可分离卷积运算
空间可分离卷积是将卷积核分解为两项独立的核分别进行操作。在数学中我们可以将矩阵分解:
[−101−202−101]=[121]×[−101]\left[ \begin{matrix} -1 & 0 & 1 \\ -2 & 0 & 2 \\ -1 & 0 & 1 \end{matrix} \right]= \left[ \begin{matrix} 1 \\ 2 \\ 1 \end{matrix} \right]\times \left[ \begin{matrix} -1 & 0 & 1 \end{matrix} \right] −1−2−1000121=121×[−101]
所以对3x3的卷积核,我们同样可以拆分成 3x1 和 1x3 的两个卷积核,对其进行卷积,且采用可分离卷积的计算量比标准卷积要少。
运算视图:
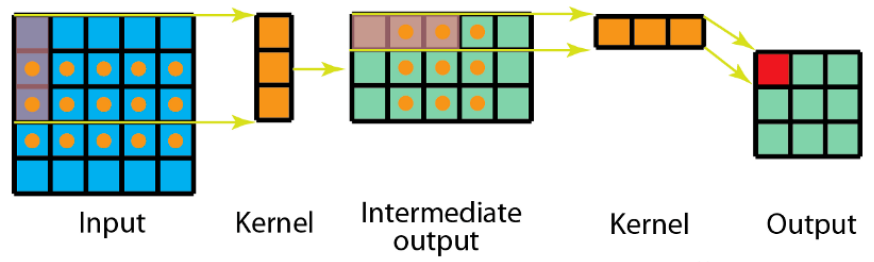
代码示例:
import torch
import torch.nn as nn
def test01():data = torch.randn(1,3,32,32)conv = nn.Conv2d(in_channels=3,#输入的特征数,通道数out_channels=3,#输出的特征数,通道数kernel_size=3,#卷积核大小stride=1,#步长)out_img = conv(data)print(out_img.shape)
def test02():#空间卷积分离data = torch.randn(1,3,32,32)#卷积核参数为3*3*1 + 3*1*3conv1 = nn.Conv2d(in_channels=3,#输入的特征数,通道数out_channels=3,#输出的特征数,通道数kernel_size=(3,1),#卷积核大小stride=1,#步长)conv2 = nn.Conv2d(in_channels=3,#输入的特征数,通道数out_channels=3,#输出的特征数,通道数kernel_size=(1,3),#卷积核大小stride=1,#步长)out_img = conv1(data)out_img = conv2(out_img)print(out_img.shape)
if __name__ == '__main__':test01()test02()
3.6深度(通道)可分离卷积
深度可分离卷积由两部组成:深度卷积核1×11\times11×1卷积,我们可以使用Animated AI官网的图来演示这一过程
图1:输入图的每一个通道,我们都使用了对应的卷积核进行卷积。 通道数量 = 卷积核个数,每个卷积核只有一个通道

图2:完成卷积后,对输出内容进行1x1的卷积

代码示例:
import torch
import torch.nn as nn
def test01():data = torch.randn(1,8,32,32)conv = nn.Conv2d(in_channels=8,#输入的特征数,通道数out_channels=8,#输出的特征数,通道数kernel_size=3,#卷积核大小stride=1,#步长)print(conv(data).shape)
def test02():# 深度分离卷积data = torch.randn(1,8,32,32)conv1 = nn.Conv2d(in_channels=8,#输入的特征数,通道数out_channels=8,#输出的特征数,通道数kernel_size=3,#卷积核大小stride=1,#步长groups=8,)conv2 = nn.Conv2d(in_channels=8,#输入的特征数,通道数out_channels=8,#输出的特征数,通道数kernel_size=1,#卷积核大小stride=1,#步长)print(conv2(conv1(data)).shape)
if __name__ == '__main__':test01()test02()
3.池化层:智能降维与空间不变性
池化层 (Pooling) 降低空间维度, 缩减模型大小,提高计算速度. 即: 主要对卷积层学习到的特征图进行下采样(SubSampling)处理。
池化层主要有两种:
-
最大池化 max pooling
最大池化是从每个局部区域中选择最大值作为池化后的值,这样可以保留局部区域中最显著的特征。最大池化在提取图像中的纹理、形状等方面具有很好的效果。
-
平均池化 avgPooling
平均池化是将局部区域中的值取平均作为池化后的值,这样可以得到整体特征的平均值。平均池化在提取图像中的整体特征、减少噪声等方面具有较好的效果。
3.1.最大池化(Max Pooling):保留最显著特征
最大池化计算方式:

代码实现:
import torch
import torch.nn as nn
torch.manual_seed(1)
data = torch.randn(1,1,5,5)
def test1(data):#最大池化print(data)#创建池化层实例pool = nn.MaxPool2d(kernel_size=2,stride=1)out = pool(data)print(out)def test4(data):#自适应最大池化pool = nn.AdaptiveMaxPool2d(output_size=4)out_data = pool(data)print(out_data)
test1(data)
test4(data)
3.2.平均池化(Average Pooling):平滑特征响应
平均池化计算方式:

代码实现:
import torch
import torch.nn as nn
torch.manual_seed(1)
data = torch.randn(1,1,5,5)
def test2(data):print(data)#平均池化pool = nn.AvgPool2d(kernel_size=2,stride=1)out = pool(data)print(out)def test3(data):print(data)#自适应平均池化pool = nn.AdaptiveAvgPool2d(output_size=4)out_data = pool(data)print(out_data)
test2(data)
test3(data)
3.3池化的作用:减少参数、控制过拟合、提供平移不变性
池化操作的优势有:
- 通过降低特征图的尺寸,池化层能够减少计算量,从而提升模型的运行效率。
- 池化操作可以带来特征的平移、旋转等不变性,这有助于提高模型对输入数据的鲁棒性。
- 池化层通常是非线性操作,例如最大值池化,这样可以增强网络的表达能力,进一步提升模型的性能。
但是池化也有缺点:
- 池化操作会丢失一些信息,这是它最大的缺点;
4.感受野:从像素到非线性概念的映射
4.1感受野定义:输出特征图中的每个单元对应输入图像的区域大小
字面意思是感受的视野范围
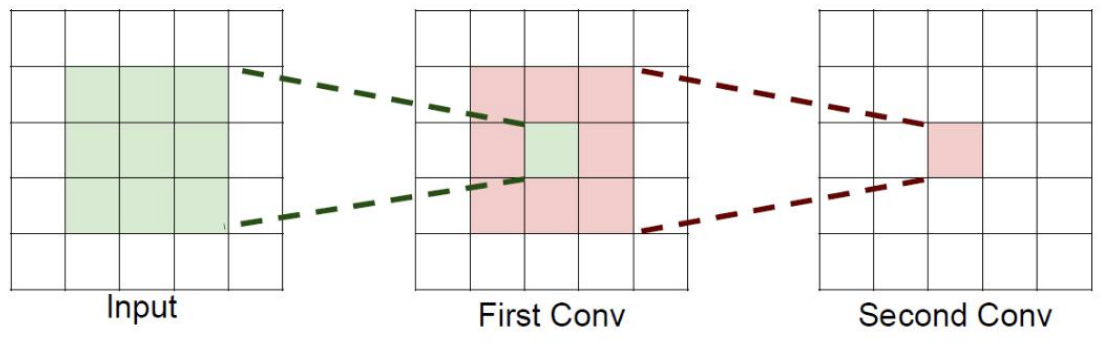
如果堆叠3个3 x 3的卷积层,并且保持滑动窗口步长为1,其感受野就是7×7的了, 这跟一个使用7x7卷积核的结果是一样的,那为什么非要堆叠3个小卷积呢?
4.2设计意义:如何设计网络结构来获得适当的感受野
假设输入大小都是h × w × C,并且都使用C个卷积核(得到C个特征图),可以来计算 一下其各自所需参数
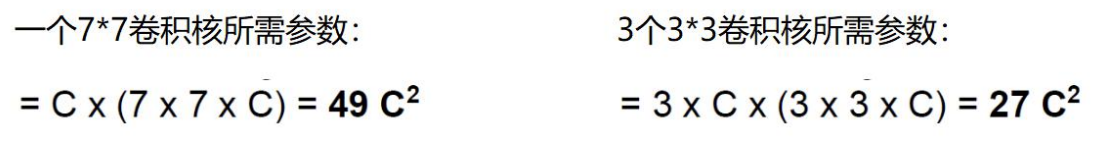
很明显,堆叠小的卷积核所需的参数更少一些,并且卷积过程越多,特征提取也会越细致,加入的非线性变换也随着增多,还不会增大权重参数个数,用小的卷积核来完成体特征提取操作。
结语
卷积神经网络通过仿生学的设计灵感,将复杂的高维图像数据转化为层次化的特征表示,奠定了现代计算机视觉的基础。理解CNN的核心组件不仅有助于模型设计,更能为解决实际视觉问题提供深刻洞察。
👀 动手实验:文中的代码示例可以帮助你直观感受卷积运算的效果!你认为CNN中最巧妙的设计是什么?欢迎在评论区分享你的观点!
📌 下篇预告:《经典CNN架构解析:从LeNet到ResNet的图像分类全解析》
