数字化转型：概念性名词浅谈（第四十二讲）

大家好，今天接着介绍数字化转型的概念性名词系列。

（1）Sigmoid函数

Sigmoid函数是一个在生物学中常见的S型函数，也称为S型生长曲线。 在信息科学中，由于其单增以及反函数单增等性质，Sigmoid函数常被用作神经网络的激活函数，将变量映射到0,1之间。

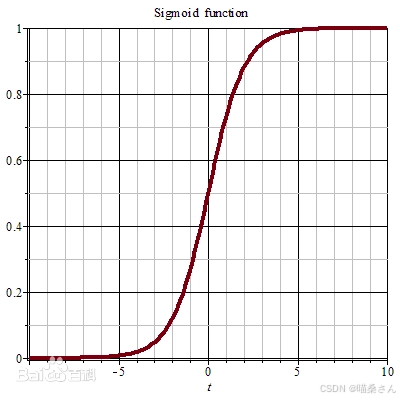
在计算机网络中，一个节点的激活函数定义了该节点在给定的输入或输入的集合下的输出。标准的计算机芯片电路可以看作是根据输入得到开（1）或关（0）输出的数字电路激活函数。这与神经网络中的线性感知机的行为类似。然而，只有非线性激活函数才允许这种网络仅使用少量节点来计算非平凡问题。 在人工神经网络中，这个功能也被称为传递函数。

sigmoid函数和tanh函数是研究早期被广泛使用的2种激活函数。两者都为S 型饱和函数。 当sigmoid 函数输入的值趋于正无穷或负无穷时，梯度会趋近零，从而发生梯度弥散现象。sigmoid函数的输出恒为正值，不是以零为中心的，这会导致权值更新时只能朝一个方向更新，从而影响收敛速度。tanh 激活函数是sigmoid 函数的改进版，是以零为中心的对称函数，收敛速度快，不容易出现 loss 值晃动，但是无法解决梯度弥散的问题。2个函数的计算量都是指数级的，计算相对复杂。softsign 函数是 tanh 函数的改进版，为 S 型饱和函数，以零为中心，值域为（−1，1）。

（2）逻辑回归

logistic回归又称logistic回归分析，是一种广义的线性回归分析模型，常用于数据挖掘，疾病自动诊断，经济预测等领域。 逻辑回归根据给定的自变量数据集来估计事件的发生概率，由于结果是一个概率，因此因变量的范围在 0 和 1 之间。例如，探讨引发疾病的危险因素，并根据危险因素预测疾病发生的概率等。以胃癌病情分析为例，选择两组人群，一组是胃癌组，一组是非胃癌组，两组人群必定具有不同的体征与生活方式等。因此因变量就为是否胃癌，值为“是”或“否”，自变量就可以包括很多了，如年龄、性别、饮食习惯、幽门螺杆菌感染等。自变量既可以是连续的，也可以是分类的。然后通过logistic回归分析，可以得到自变量的权重，从而可以大致了解到底哪些因素是胃癌的危险因素。同时根据该权值可以根据危险因素预测一个人患癌症的可能性。

logistic回归是一种广义线性回归（generalized linear model），因此与多重线性回归分析有很多相同之处。它们的模型形式基本上相同，都具有 w‘x+b，其中w和b是待求参数，其区别在于他们的因变量不同，多重线性回归直接将w‘x+b作为因变量，即y =w‘x+b，而logistic回归则通过函数L将w‘x+b对应一个隐状态p，p =L(w‘x+b),然后根据p 与1-p的大小决定因变量的值。如果L是logistic函数，就是logistic回归，如果L是多项式函数就是多项式回归。 

logistic回归的因变量可以是二分类的，也可以是多分类的，但是二分类的更为常用，也更加容易解释，多类可以使用softmax方法进行处理。实际中最为常用的就是二分类的logistic回归。 

Logistic回归模型的适用条件

1 因变量为二分类的分类变量或某事件的发生率，并且是数值型变量。但是需要注意，重复计数现象指标不适用于Logistic回归。

2 残差和因变量都要服从二项分布。二项分布对应的是分类变量，所以不是正态分布，进而不是用最小二乘法，而是最大似然法来解决方程估计和检验问题。

3 自变量和Logistic概率是线性关系

4 各观测对象间相互独立。 

原理：如果直接将线性回归的模型扣到Logistic回归中，会造成方程二边取值区间不同和普遍的非直线关系。因为Logistic中因变量为二分类变量，某个概率作为方程的因变量估计值取值范围为0-1，但是，方程右边取值范围是无穷大或者无穷小。所以，才引入Logistic回归。 

Logistic回归实质：发生概率除以没有发生概率再取对数。就是这个不太繁琐的变换改变了取值区间的矛盾和因变量自变量间的曲线关系。究其原因，是发生和未发生的概率成为了比值 ，这个比值就是一个缓冲，将取值范围扩大，再进行对数变换，整个因变量改变。不仅如此，这种变换往往使得因变量和自变量之间呈线性关系，这是根据大量实践而总结。所以，Logistic回归从根本上解决因变量要不是连续变量怎么办的问题。还有，Logistic应用广泛的原因是许多现实问题跟它的模型吻合。例如一件事情是否发生跟其他数值型自变量的关系。 

注意：如果自变量为字符型，就需要进行重新编码。一般如果自变量有三个水平就非常难对付，所以，如果自变量有更多水平就太复杂。这里只讨论自变量只有三个水平。非常麻烦，需要再设二个新变量。共有三个变量，第一个变量编码1为高水平，其他水平为0。第二个变量编码1为中间水平，0为其他水平。第三个变量，所有水平都为0。实在是麻烦，而且不容易理解。最好不要这样做，也就是，最好自变量都为连续变量。 

spss操作：进入Logistic回归主对话框，通用操作不赘述。

发现没有自变量这个说法，只有协变量，其实协变量就是自变量。旁边的块就是可以设置很多模型。

“方法”栏：这个根据词语理解不容易明白，需要说明。

共有7种方法。但是都是有规律可寻的。

“向前”和“向后”：向前是事先用一步一步的方法筛选自变量，也就是先设立门槛。称作“前”。而向后，是先把所有的自变量都进来，然后再筛选自变量。也就是先不设置门槛，等进来了再一个一个淘汰。

“LR”和“Wald”,LR指的是极大偏似然估计的似然比统计量概率值，有一点长。但是其中重要的词语就是似然。

Wald指Wald统计量概率值。

“条件”指条件参数似然比统计量概率值。

“进入”就是所有自变量都进来，不进行任何筛选

将所有的关键词组合在一起就是7种方法，分别是“进入”“向前LR”“向前Wald”"向后LR"“向后Wald”“向后条件”“向前条件”

下一步：一旦选定协变量，也就是自变量，“分类”按钮就会被激活。其中，当选择完分类协变量以后，“更改对比”选项组就会被激活。一共有7种更改对比的方法。

“指示符”和“偏差”，都是选择最后一个和第一个个案作为对比标准，也就是这二种方法能够激活“参考类别”栏。“指示符”是默认选项。“偏差”表示分类变量每个水平和总平均值进行对比，总平均值的上下界就是"最后一个"和"第一个"在“参考类别”的设置。

“简单”也能激活“参考类别”设置。表示对分类变量各个水平和第一个水平或者最后一个水平的均值进行比较。

“差值”对分类变量各个水平都和前面的水平进行作差比较。第一个水平除外，因为不能作差。

“Helmert”跟“差值”正好相反。是每一个水平和后面水平进行作差比较。最后一个水平除外。仍然是因为不能做差。

“重复”表示对分类变量各个水平进行重复对比。

“多项式”对每一个水平按分类变量顺序进行趋势分析，常用的趋势分析方法有线性二次式。

逻辑回归模型分为三种类型，它们基于分类响应而定义。 

• 二元逻辑回归：在这种方法中，响应变量或因变量本质上为二分法，即它只有两种可能的结果（如 0 或 1）。 它的一些流行使用示例包括预测电子邮件是否为垃圾邮件，或者肿瘤是恶性还是良性。 在逻辑回归中，这是最常见的使用方法，更概括地说，它是二元分类最常见的分类器之一。 

• 多项逻辑回归：在这种类型的逻辑回归模型中，因变量具有三个或更多可能的结果；但是，这些值并没有指定的顺序。 例如，电影制片厂想要预测影院观众可能会看什么类型的电影，从而更有效地推销电影。 多项逻辑回归模型可以帮助制片厂确定一个人的年龄、性别和约会状态对他们喜欢的电影类型所产生的影响程度。 然后，制片厂可以锁定潜在观众人群，向他们发布特定电影的广告。 

• 序数逻辑回归：当响应变量具有三个或更多可能的结果时，会利用这种类型的逻辑回归模型，但在这种情况下，这些值确实具有定义的顺序。 序数响应的示例包括从 A 到 F 的分级量表或从 1 到 5 的评分量表。

本篇文章要介绍的就是这么多，我们下篇文章再见。