算法题记录01：

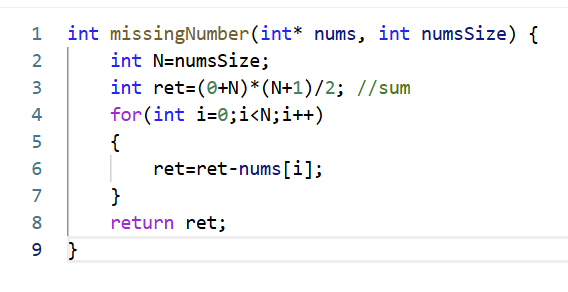
01.消失的数字

缺点：排序的复杂度。

缺点：n太大存在整数溢出风险。

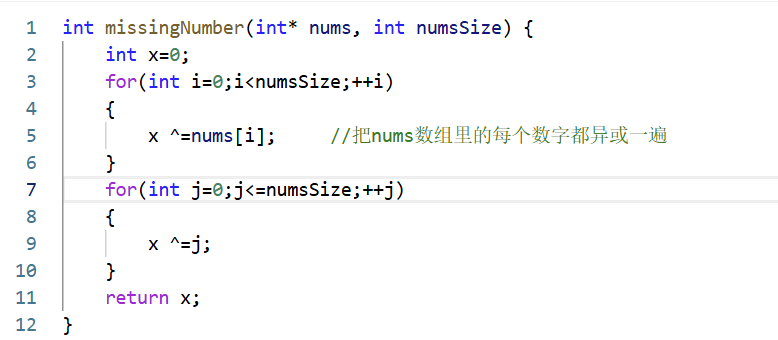
思路3：异或：相同为0，相异为1。

✅ 数学原理（异或性质）

• 任何数和自身异或结果为 0：a ^ a = 0

• 任何数和 0 异或结果是它本身：a ^ 0 = a

（​多位整数的异或是按位运算，每一位都独立地遵循单位异或的真值表）

a   = 11010110
0   = 00000000
a^0 = 11010110

• 异或满足交换律和结合律：a ^ b ^ c = c ^ a ^ b

• 相同的数异或后为0

✅ 具体实现：

第一步：异或数组中实际存在的数字

第二步：异或应该出现的所有数字（0 到 numsSize）

[nums[0],nums[i]]

[0,N]

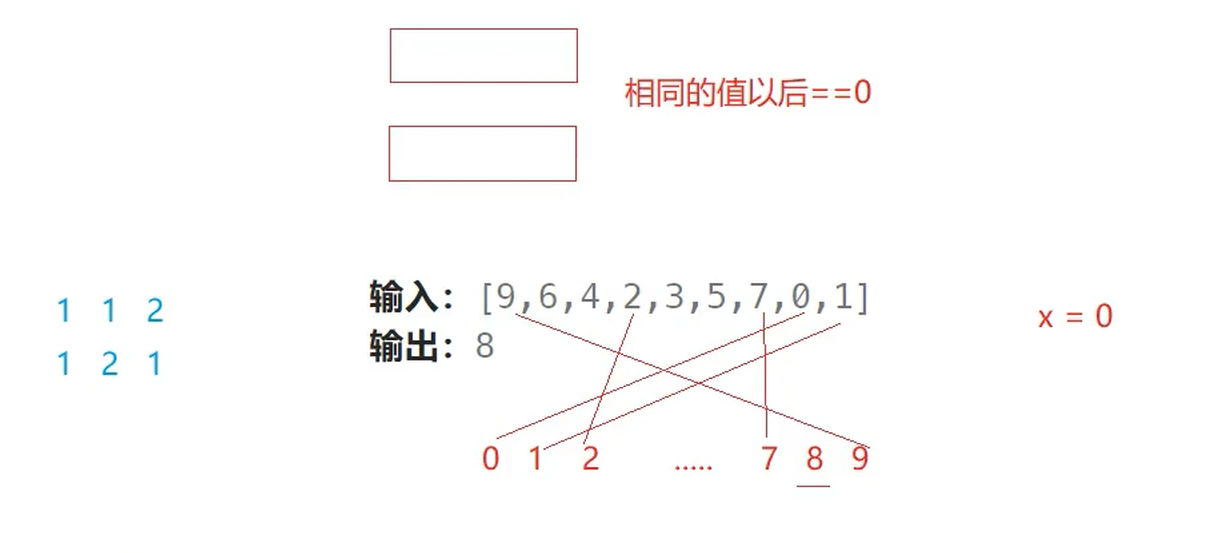
本质：       

         0         ^         数组里本应该存在的         ^         数组里实际存在的

                （原理：交换律    且        相同的数异或后为0）

两两一对，则最后剩下的那个数（单独的）就是答案。

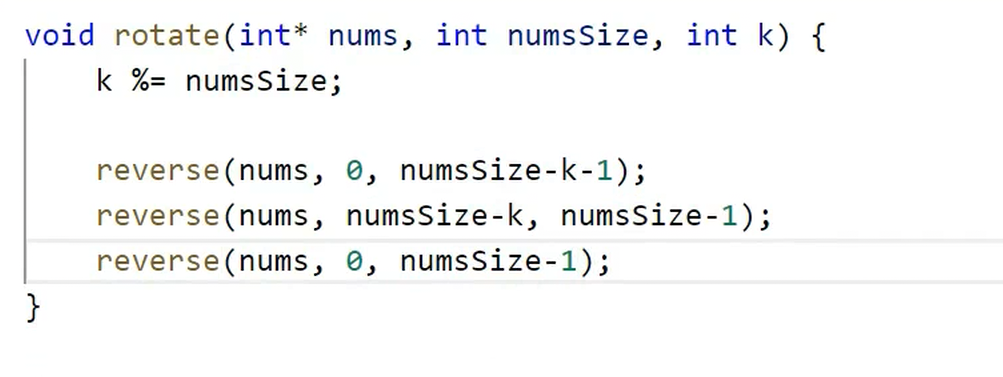
02.轮转数组

思路一.

真实的旋转次数k=k%N 

总共移动：

1到k，共k次

每次移动：

先保存最后一位，再依次右边移动其他位，一共移动（N-2）次。最后把最后一位放到第一位。（下标   0-N-2）

| 写法    | 含义       | 循环控制表达式里实际用哪个值  |
| `i--` | **先用后减** | 用 `i` 的旧值，再减 1  |
| `--i` | **先减后用** | 先把 `i` 减 1，再用新值 |

缺点：N^2的算法不给过。

思路二：三段逆置