当前位置：首页 > news >正文

排序---插入排序

news 2025/8/23 10:48:07

基本思想

对于插入排序而言，它的基本思想就是往已经排好序的序列里边插入数据。思想类似于玩扑克牌。接下来的排序都是基于下边的这个数组。

int a[ ] = { 5 , 3 , 9 , 6 , 2 , 4 , 7 , 1 , 8 };

直接插入排序

我们想要将这个数组排成升序，在最一开始，我们可以认为数组的第一个元素5为一个有序的序列，5之后的元素就是一个个要往5这个有序的序列里边插入的元素。

3显然比5要小，要想排成升序，那么5就要移动到3的位置，3插入到5原来的位置。接下来的操作其实也是这样的。

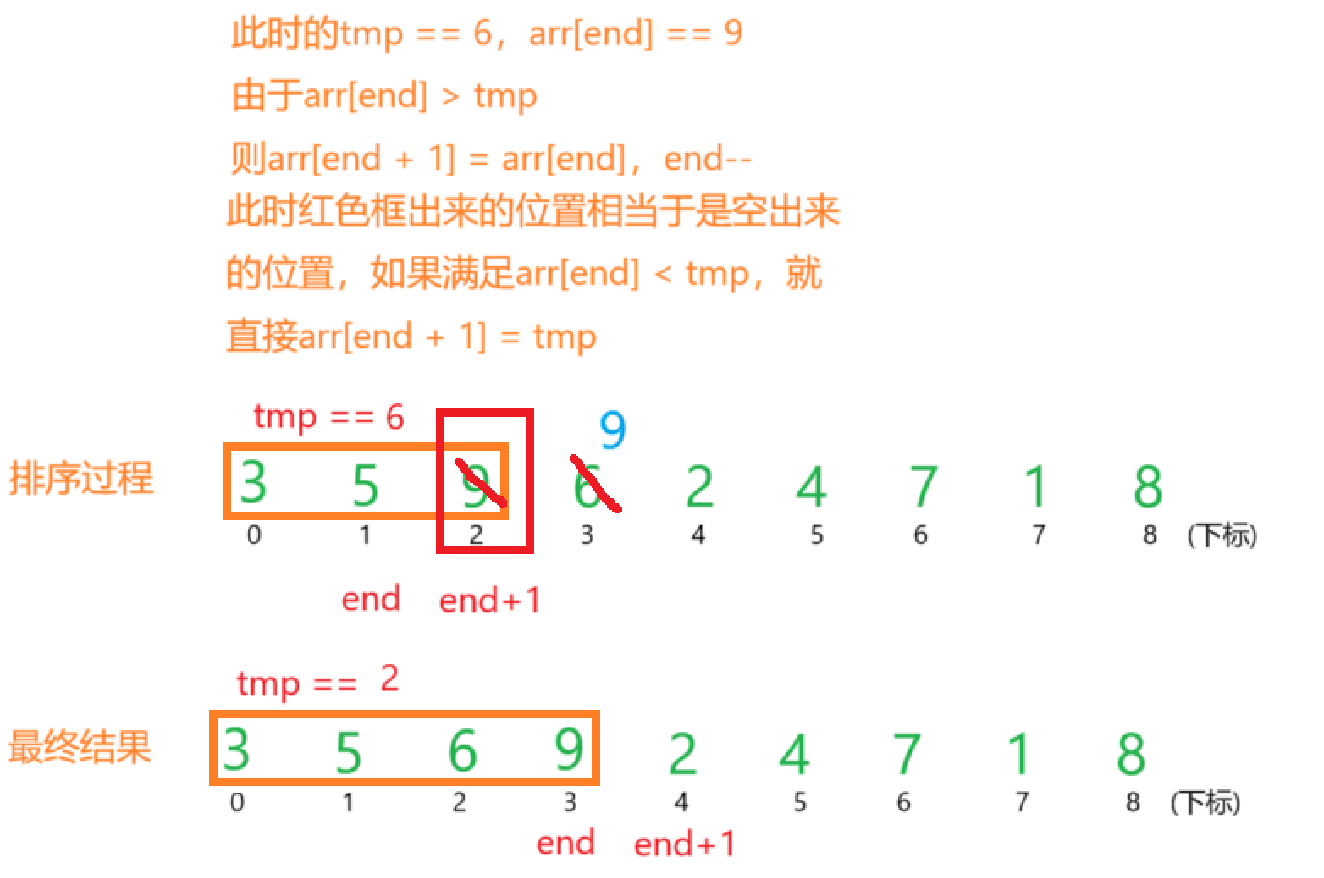
为了完成上边的操作，我们需要一个变量tmp去存储要插入的数据，我们还需要变量end去标记有序序列里边的最后一个元素，那么end + 1就表示的是待排序序列里边的第一个元素。

有了上边的铺垫，代码的基本思路就出来了。拿end + 1位置的元素先给给tmp，接着拿end位置的元素与tmp做比较。如果arr[end] > tmp，就直接把arr[end + 1] = arr[end]，可是到这，tmp依旧没有到它该去的有序的位置，所以end--，此时再重复上边的过程，直到arr[end] < tmp，这时候把arr[end + 1] = tmp。

顺着上边的思路，大家再结合我下边的图片理解。

具体代码

//直接插入排序
void InsertSort(int* arr, int n)
{for (int i = 0; i < n - 1; i++){int end = i;int tmp = arr[end + 1];while (end >= 0){if (arr[end] > tmp){arr[end + 1] = arr[end];end--;}else{break;}}arr[end + 1] = tmp;}
}

从具体的代码里边还需要注意几点，一方面是arr[end] < tmp的时候，将arr[end + 1] = tmp，另一方面，如果tmp的大小比有序序列里边都小，那么tmp这时候其实是去的0下标的位置，此时end < 0，所以统一把arr[end + 1] = tmp写在循环外边。还有最外边的那个for循环，i < n - 1，因为如果i == n的时候，end + 1已经越界了。

直接插入排序的时间复杂度

直接插入排序是由两个循环嵌套而成的，最终的时间复杂度可以理解为最深层那行代码执行的次数，假设if条件永远成立，这是最坏的情况。可以画个大概的表格来理解。

end = i         执行次数
      0    1
      1 2
      2 3
      . .
      . .
      . .
n - 2 n - 1

最后用等差数列求和一下，然后按照大0表示法的条件，得出时间复杂度最差的情况为0(N^2)。当大的数据全在前边，小的数据全在后边才能满足这一个情况。但如果这个数组有序(小的元素都在前边，大的数据都在后边)，那么时间复杂度就降为0(N)了。

为了满足每次待排序的序列都可以满足小的数据大都在前边，大的数据大都在后边，我们就需要采取一些优化的手段，希尔排序可以帮助我们。

希尔排序

希尔排序是直接插入排序的优化版本，它的基本思想就是将待排序序列先分组，组内先排序，最后大致满足小的数据在前，大的数据在后了之后，再进行直接插入排序。

希尔排序法又叫缩小增量法，具体的实现就是先选定⼀个整数（通常是gap = n/3+1），把待排序序列所有记录分成各组，所有的距离相等的记录分在同⼀组内，并对每⼀组内的记录进⾏排序，然后gap=gap/3+1得到下⼀个整数，再将数组分成各组，进⾏插⼊排序，当gap=1时，就相当于直接插⼊排序。gap为几，就分为几组。

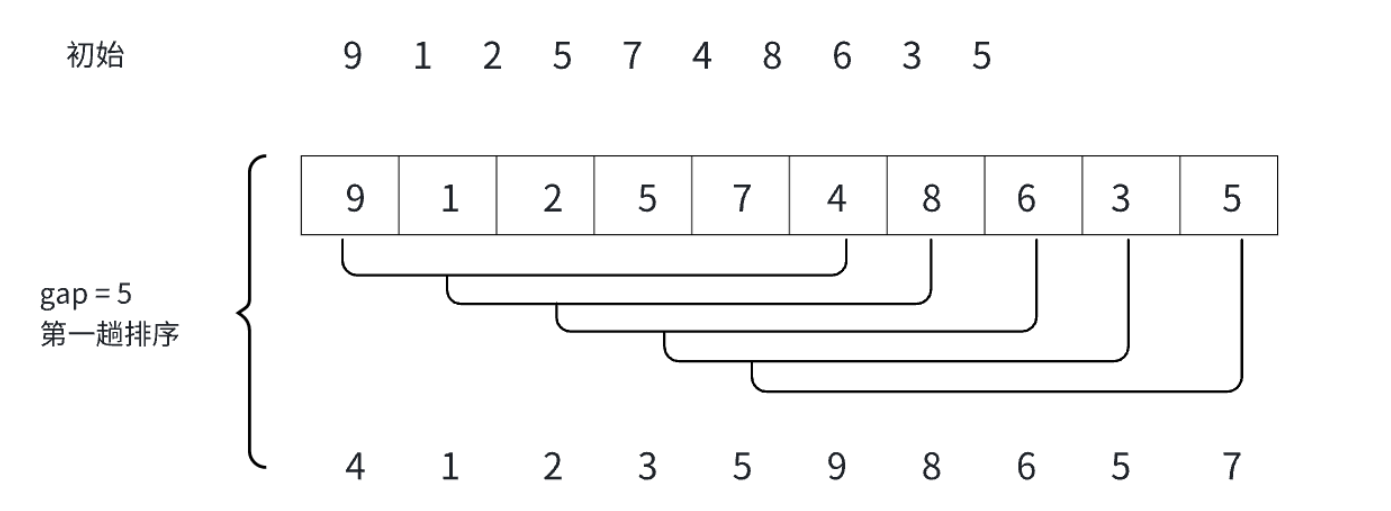
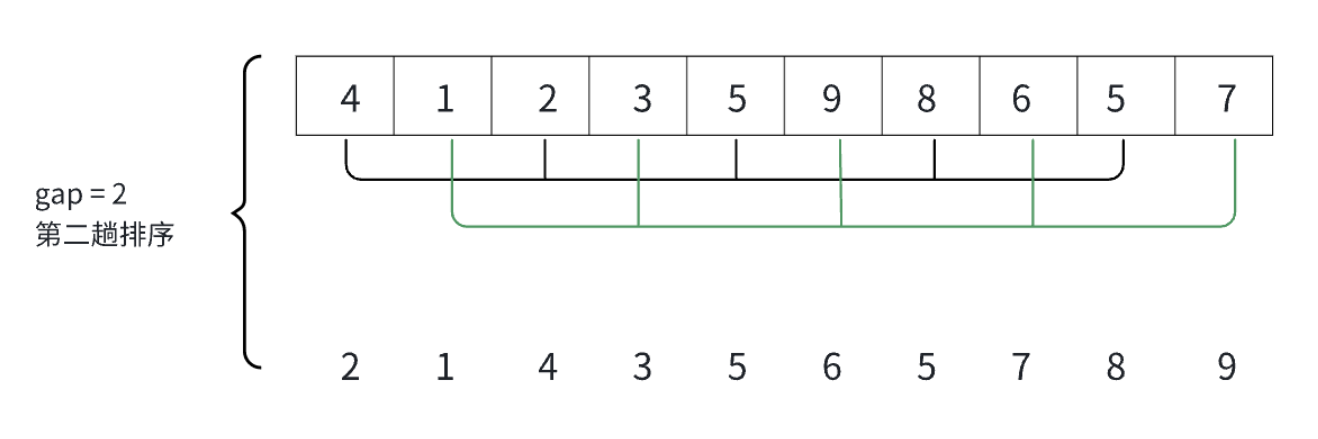
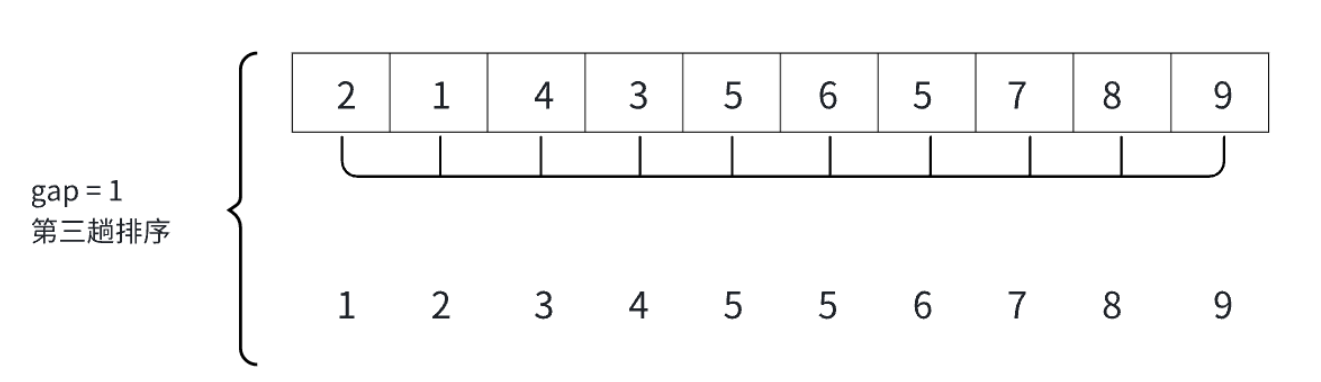
这就是完整的分组情况。

就拿gap == 2来具体说明。

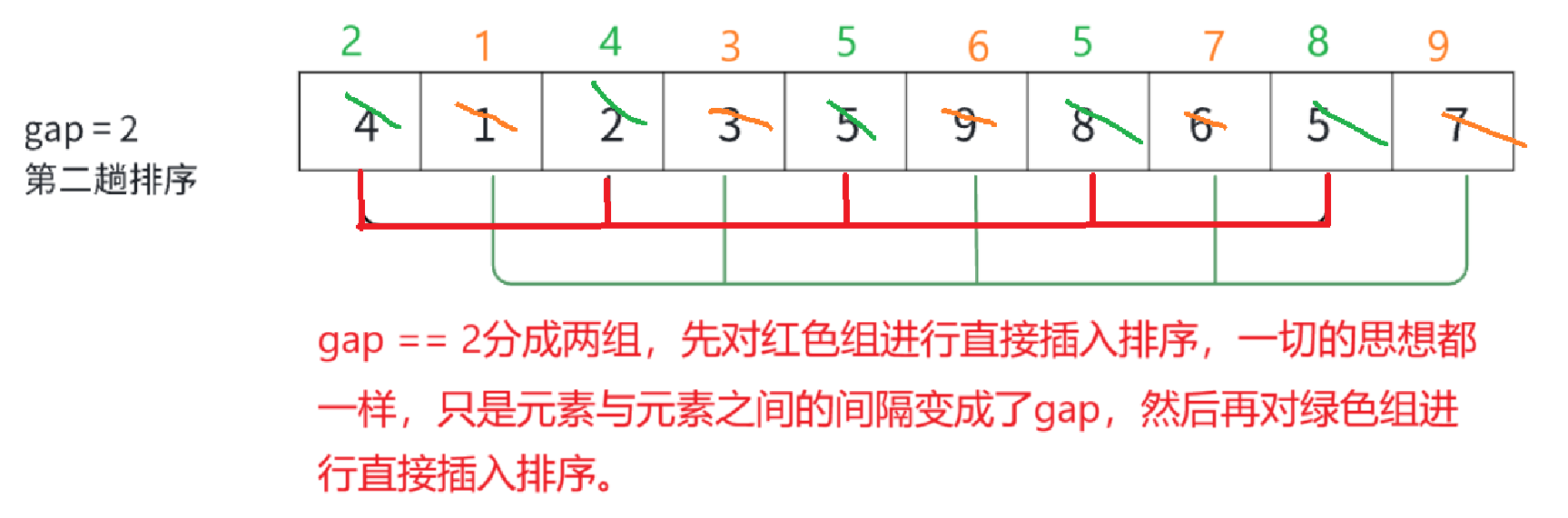
很直观的可以看出，经过了两次分组，并且组内排序之后，元素变成了我们最希望看到的样字，小的全在前边，大的都在后边。

我们称gap > 1为预排序，而gao == 1就为直接插入排序。这是一个优化的过程，本质还是直接插入排序，整体代码变化不大。

代码实现

//希尔排序
void ShellSort(int* arr, int n)
{int gap = n;while(gap > 1)//gap > 1都是预排序{gap = gap / 3 + 1;for (int i = 0; i < n - gap; i++){int end = i;int tmp = arr[end + gap];while (end >= 0){if (arr[end] > tmp){arr[end + gap] = arr[end];end = end - gap;}else{break;}}arr[end + gap] = tmp;}}
}

对于最外层的while循环来说很好理解，因为循环里边都是在进行预排序，所以要满足gap > 1，除去for循环的循环条件不看，其他的代码就是直接插入排序一样的代码，只不过是元素之间的距离变成了gap，对于for循环来说，为什么要i < n - gap，是因为我们简化了代码，如果真的按照一组组去进行排序的话，就要再多嵌套了个循环了，这显然不合适，所以我们就对各组同时进行直接插入排序。

还是拿gap == 2为例子(上边有图)，gap为2的时候总共分为两组，i = 0的时候进入for循环就是在对红色组进行排序，排序完，i++，再进入for循环，就是在对绿色组进行排序，以此类推，又由于每组之间的元素相差gap，所以当end == n - gap的时候已经是在最后一个元素的位置，再往下end + gap就越界了。