当前位置：首页 > news >正文

【MATLAB技巧】已知平面上的一些点，拟合得到一个圆的例程，给出最小二乘与非线性迭代两种解法，附下载链接

news 2025/8/15 13:56:56

在这里插入图片描述

本文所述代码用于对带噪声的圆形数据进行拟合，并比较代数法与非线性最小二乘法的效果。
代码先生成已知圆心与半径的测试点并加噪声，然后用线性方程组解法快速估计圆心与半径（代数法），再以此结果为初值，通过最小化点到圆的距离平方和（非线性法）获得更精确参数，最后绘制原始点与两种拟合圆进行对比。

文章目录

运行结果
算法介绍
- 1. 功能概述
- 2. 核心公式
MATLAB源代码
方法选择建议

运行结果

原始数据点与拟合后的圆形绘图示例：
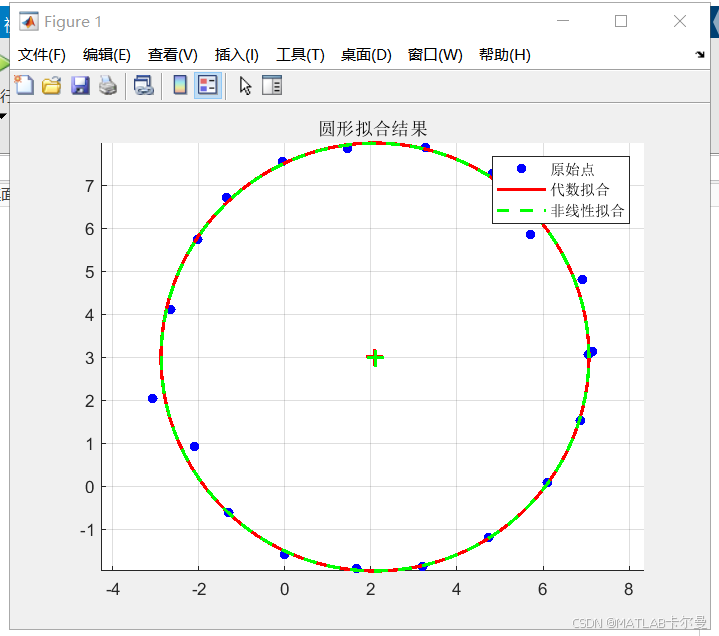
在这里插入图片描述

数据输出：
在这里插入图片描述

算法介绍

1. 功能概述

数据生成：首先构造一个已知圆心 (2,3)、半径 5 的圆形点集，并加入随机噪声。
拟合方法：
1. 代数拟合法（线性法）：通过解线性方程组快速估计圆心和半径。
2. 非线性拟合法：以代数拟合结果为初值，利用 fmincon 最小化点到圆的距离平方和，得到更精确结果。
结果对比：输出两种方法的圆心、半径以及残差。
可视化：绘制原始数据点、两种拟合圆及其圆心，比较拟合效果。

2. 核心公式

(1) 圆的方程

一个圆在二维平面上的标准方程为：

$x - x_c)^2 + (y - y_c)^2 = r^2$

其中：

$x_c, y_c)$ 为圆心坐标
$r$ 为半径

(2) 代数法推导

将圆方程展开：

$x^2 + y^2 - 2x_c x - 2y_c y + (x_c^2 + y_c^2 - r^2) = 0$

设：

$-2x_c,\quad E = -2y_c,\quad F = x_c^2 + y_c^2 - r^2$

则有：

$x^2 + y^2 + D x + E y + F = 0$

$p = A^{-1}b$

进而得到半径：

$\sqrt{c + x_c^2 + y_c^2}$

(3) 非线性最小二乘法

目标是最小化点到圆的距离与半径差的平方和：

$J(xc,yc,r)=∑i=1n((xi−xc)2+(yi−yc)2−r)2J(x_c, y_c, r) = \sum_{i=1}^n \left( \sqrt{(x_i - x_c)^2 + (y_i - y_c)^2} - r \right)^2$

使用 fmincon 在半径 $r > 0$ 的约束下进行优化。

MATLAB源代码

程序结构：
在这里插入图片描述
部分代码：

clc;clear;close all;
rng(0);
% 生成测试数据（带噪声的圆）
true_center = [2, 3];
true_radius = 5;
theta = linspace(0, 2*pi, 20);
noise = 0.1 * randn(size(theta));x = true_center(1) + true_radius * cos(theta) + noise;
y = true_center(2) + true_radius * sin(theta) + noise;% 方法一：代数拟合
[center1, radius1, residual1] = fitCircle(x, y);% 方法二：非线性拟合
[center2, radius2] = fitCircleNonlinear(x, y);% 显示结果
fprintf('真实圆心: (%.2f, %.2f), 真实半径: %.2f\n', true_center, true_radius);
fprintf('代数拟合 - 圆心: (%.2f, %.2f), 半径: %.2f, 残差: %.4f\n', center1, radius1, residual1);
fprintf('非线性拟合 - 圆心: (%.2f, %.2f), 半径: %.2f\n', center2, radius2);