当前位置：首页 > news >正文

【CF】Day127——杂题 (数论 gcd | 数论 gcd | 博弈论 | 二分图判断 | 贪心 + 暴力 / 二分答案 | 数论 gcd + 动态规划)

news 2025/8/15 13:28:37

D. Lucky Chains

题目：

思路：

数学

题目意思就是让我们求得一个最小的 k，使得 gcd(x + k, y + k) > 1

那么我们考虑 gcd 的性质：gcd(a, b) = gcd(a,b - a)

则原式化简为 gcd(x + k, y + k) = gcd(x + k, y - x)，此时显然简单很多了，即我们要找到一个 k，使得 x + k 与 y - x 不互质

由于 y - x 是一个定值，所以我们提前计算即可，那么现在考虑计算 k

我们假设二者的 gcd 为 p，那么就有 p | x + k 且 p | y - x，所以我们考虑枚举 y - x 的质因数来求出 p 即可，那么则有以下式子

(x + k) % p == 0，即 (x % p + k % p) % p == 0，所以我们考虑先计算 x % p 的值，然后借此计算 k 的值

令 x % p = m，若 m = 0，则 k = p，否则 k = p - m

最后开局特判一下需不需要求解 0 即可

代码：

#include <bits/stdc++.h>
using namespace std;
#define yes cout << "YES\n"
#define no cout << "NO\n"
vector<int> prime;
int nop[100005];void init()
{nop[0] = nop[1] = 1;for (int i = 2; i <= 100000; i++){if(!nop[i]) prime.push_back(i);for (int j = 0; j < prime.size() && i * prime[j] <= 100000; j++){nop[i * prime[j]] = 1;if(i % prime[j] == 0) break;}}
}void solve()
{int x,y;cin >> x >> y;if(gcd(x,y) != 1){cout << "0\n";return;}int dis = y - x;if(dis == 1){cout << "-1\n";return;}set<int> fac;for (auto & i : prime){if(i * i > dis) break;if(dis % i == 0){while (dis % i == 0){dis /= i;}fac.insert(i);}}if(dis > 1)fac.insert(dis);int d = 1e9;for(auto & p : fac){int yu = x % p;int td = 0;if(yu == 0)td = p;elsetd = p - yu;d = min(d,td);}cout << d << endl;
}signed main()
{init();ios::sync_with_stdio(false);cin.tie(nullptr);int t = 1;cin >> t;while (t--){solve();}return 0;
}

C. Koxia and Number Theory

题目：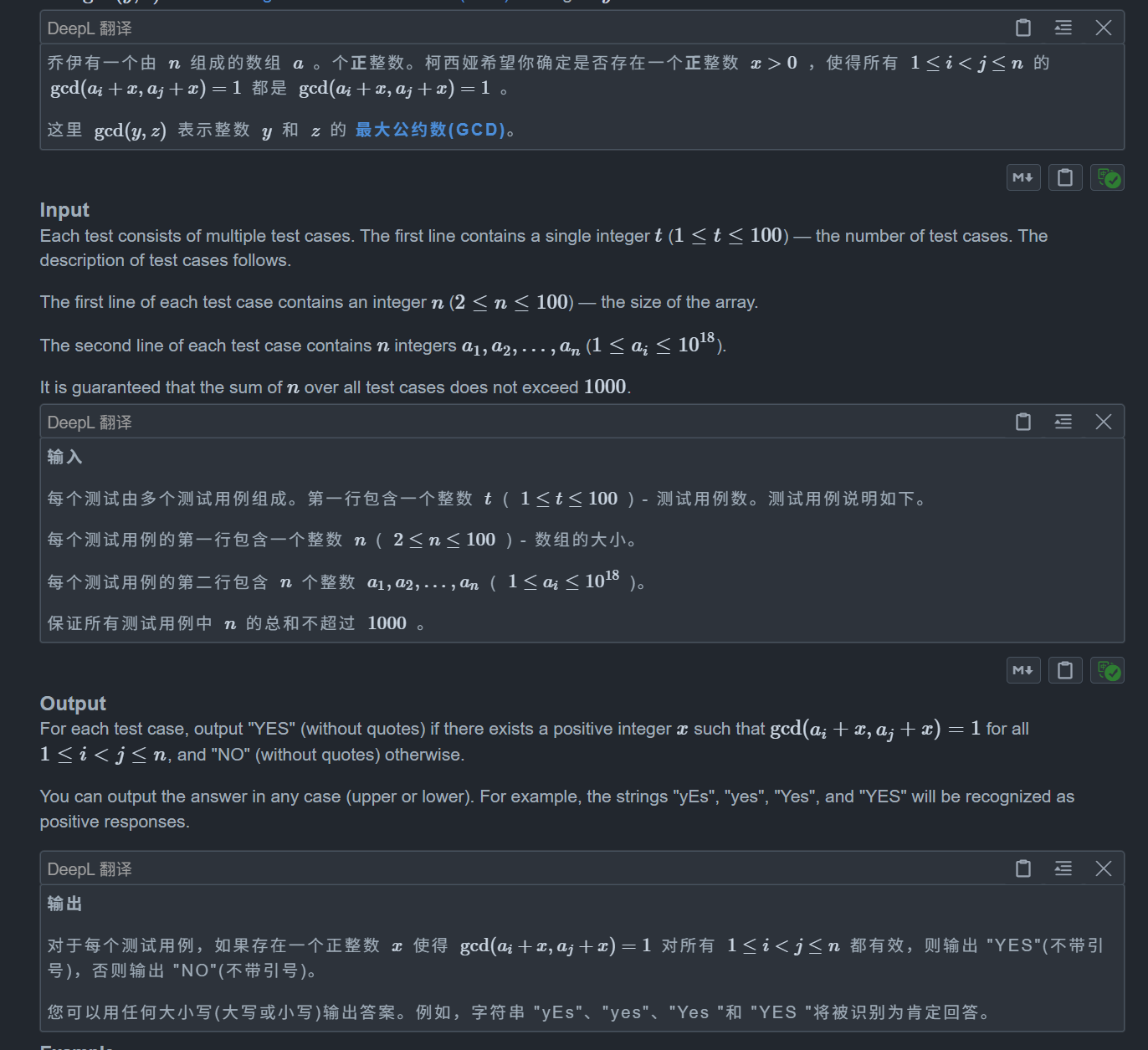

思路：

和上题很像，但是不一样

我们不妨想想什么情况下无解，如果有两个同样的数，那么显然无解，那么还有什么时候呢？

注意到题目让我们对每个 ai 都加上了 x，同时 x > 0，那么如果考虑一个 k，记 sum[i] 表示 a[j] 模 k 为 i 的数量，如果对于 sum[0] ~ sum[k - 1] 都大于等于 2，那么显然是无解的，因为此时我们无论相加多少都会存在两个数 gcd 不等于 1，即会存在两个均为 k 的倍数的数，这里我们可以选 k 为质数，虽然合数也没问题，但是质数更好判断

来自luogu题解 CF1770C【Koxia and Number Theory】 - 洛谷专栏：

代码：

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define yes cout << "YES\n"
#define no cout << "NO\n"void solve()
{int n;cin >> n;vector<int> a(n);set<int> st;int flag = 0;for (int i = 0; i < n; i++){cin >> a[i];if(st.count(a[i])) flag = 1;else st.insert(a[i]);}if(flag){no;return;}//对于模数 i 模完剩 j 的个数vector<vector<int>> modcnt(105,vector<int>(105,0));for (int k = 2; k <= n; k++){for (int i = 0; i < n; i++){modcnt[k][a[i] % k]++;}int f = 1;for (int i = 0; i < k; i++){if(modcnt[k][i] < 2){f = 0;break;}}if(f){no;return;}} yes;
}signed main()
{ios::sync_with_stdio(false);cin.tie(nullptr);int t = 1;cin >> t;while (t--){solve();}return 0;
}

E. Permutation Game

题目：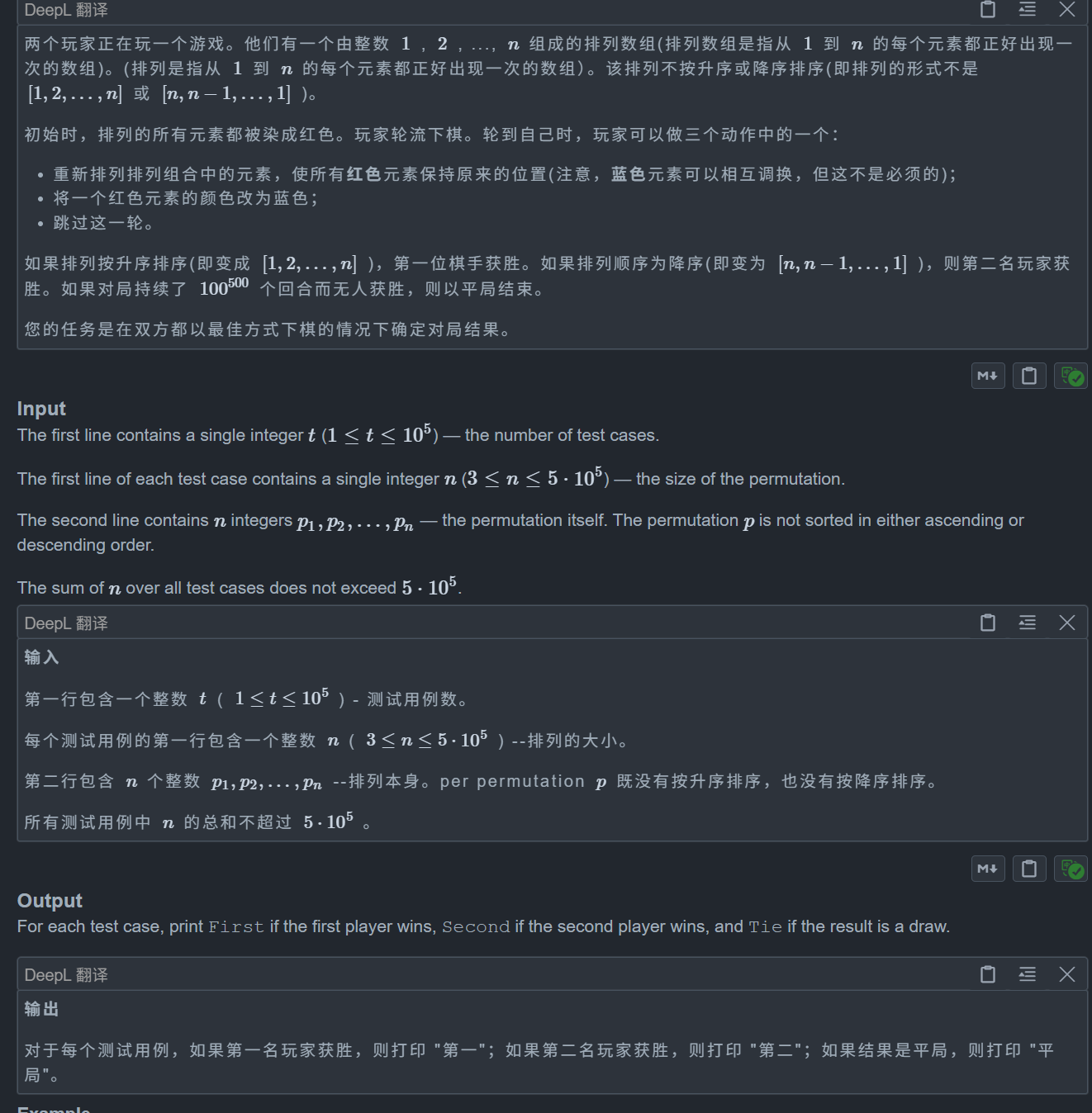

思路：

不难的博弈

题目和一般博弈不一样，还给出了一个平局结局，看起来更难，实则更简单

一个显然的胜利条件就是需要涂的少的人必胜

我们假设第一个人要涂 a 个格子，第二个人涂 b 个格子，他们都要涂 c 个格子

那么只有在 a + c <= b 时先手赢，且只有在 c + b < a 时后手赢

为什么呢？我们考虑一点，如果 a + c < b，假设 a + c = b - 1，那么最后一定是就剩一个他们都要涂的格子了，此时谁涂了谁就输了，所以干脆不动，那么就平局

后者同理，只不过由于是后手，所以还要多一步，模拟即可

代码：

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define yes cout << "YES\n"
#define no cout << "NO\n"void solve()
{int n;cin >> n;vector<int> a(n + 1);//正向需要涂 f 个，逆向需要涂 s 个，两个都需要涂 m 个int f = 0, s = 0, m = 0;for (int i = 1; i <= n; i++){cin >> a[i];if (a[i] == i)f++;if (a[i] == n - i + 1)s++;if (a[i] != i && a[i] != n - i + 1)m++;}f = n-f;s = n-s;if (f + m <= s){cout << "First\n";return;}if (s + m < f){cout << "Second\n";return;}cout << "Tie\n";
}signed main()
{ios::sync_with_stdio(false);cin.tie(nullptr);int t = 1;cin >> t;while (t--){solve();}return 0;
}

A. Amazing Trick

题目：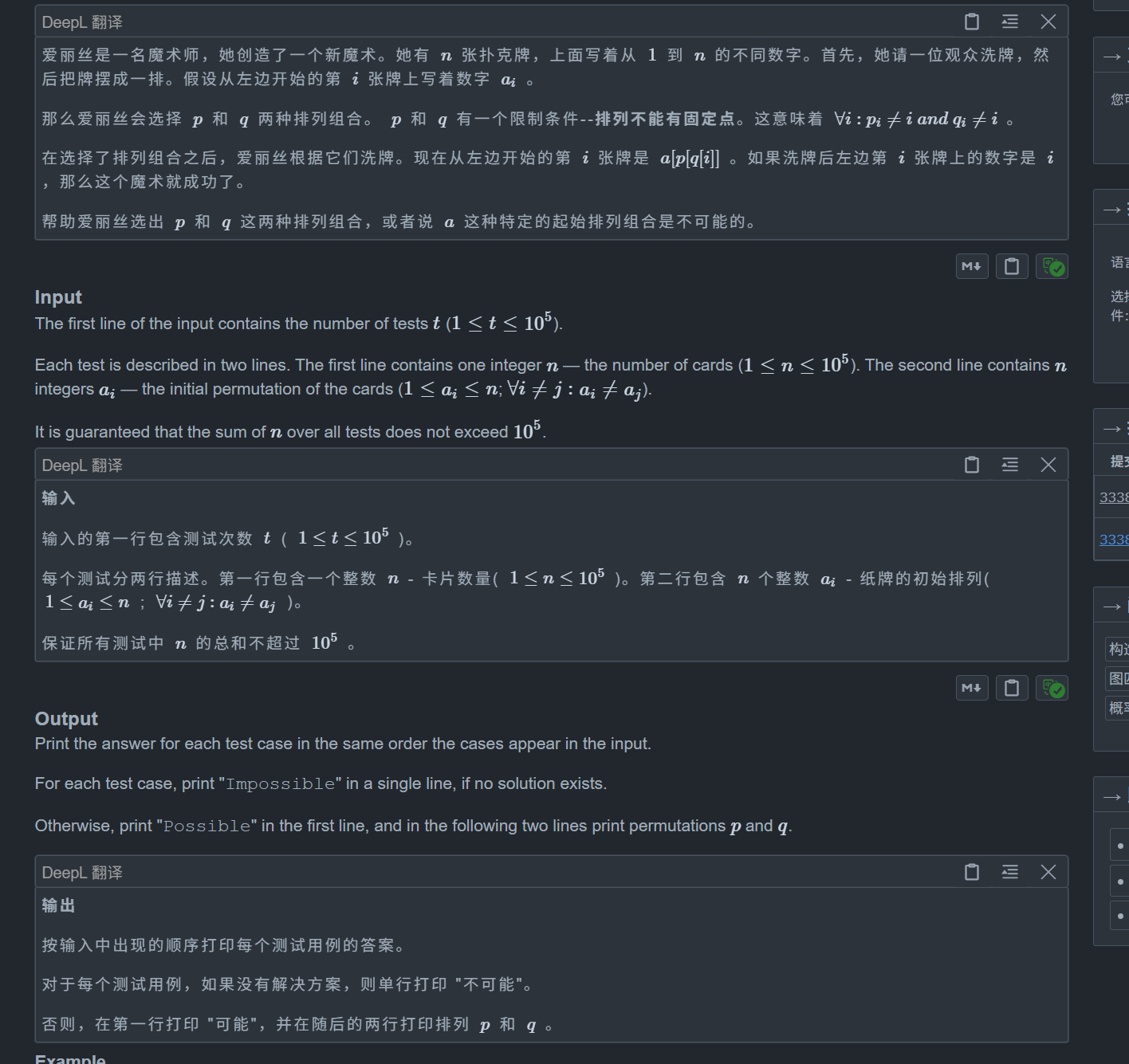

思路：

如题目一样

我们对于 3 以下的很显然暴力枚举就行，考虑 n >= 4

我们其实不难发现此时每个节点都有两个限制，一个是自生不能等于 i，一个是子节点的对应值也不能等于 i，那么就相当于最多有两个限制，而每个节点都有起码有两个度，试着考虑一个置换环，那么就相当于我们要构造 n 个置换环即可，可猜测 n>= 4 一定可以

所以随机枚举排列即可，这里使用shuffle随机

证明可看CF1773A Amazing Trick（随机/Hall定理） - 洛谷专栏

代码：

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define yes cout << "YES\n"
#define no cout << "NO\n"
mt19937 rnd(chrono::steady_clock::now().time_since_epoch().count());
int n;
int a[100005],p[100005],q[100005];
void solve()
{cin >> n;for (int i = 1; i <= n; i++){cin >> a[i];p[i] = i;}for (int i = 1; i <= 1000; i++){shuffle(p+1,p+1+n,rnd);int flag = 1;for (int i = 1; i <= n && flag; i++){if(p[i] == i || a[p[i]] == i){flag = 0;}else{q[a[p[i]]] = i;}}if(flag){cout << "Possible\n";for (int i = 1; i <= n; i++){cout << p[i] << " ";}cout << endl;for (int i = 1; i <= n; i++){cout << q[i] << " ";}cout << endl;return;}}  cout << "Impossible\n";
}signed main()
{ios::sync_with_stdio(false);cin.tie(nullptr);int t = 1;cin >> t;while (t--){solve();}return 0;
}

B. Make It Equal

题目：

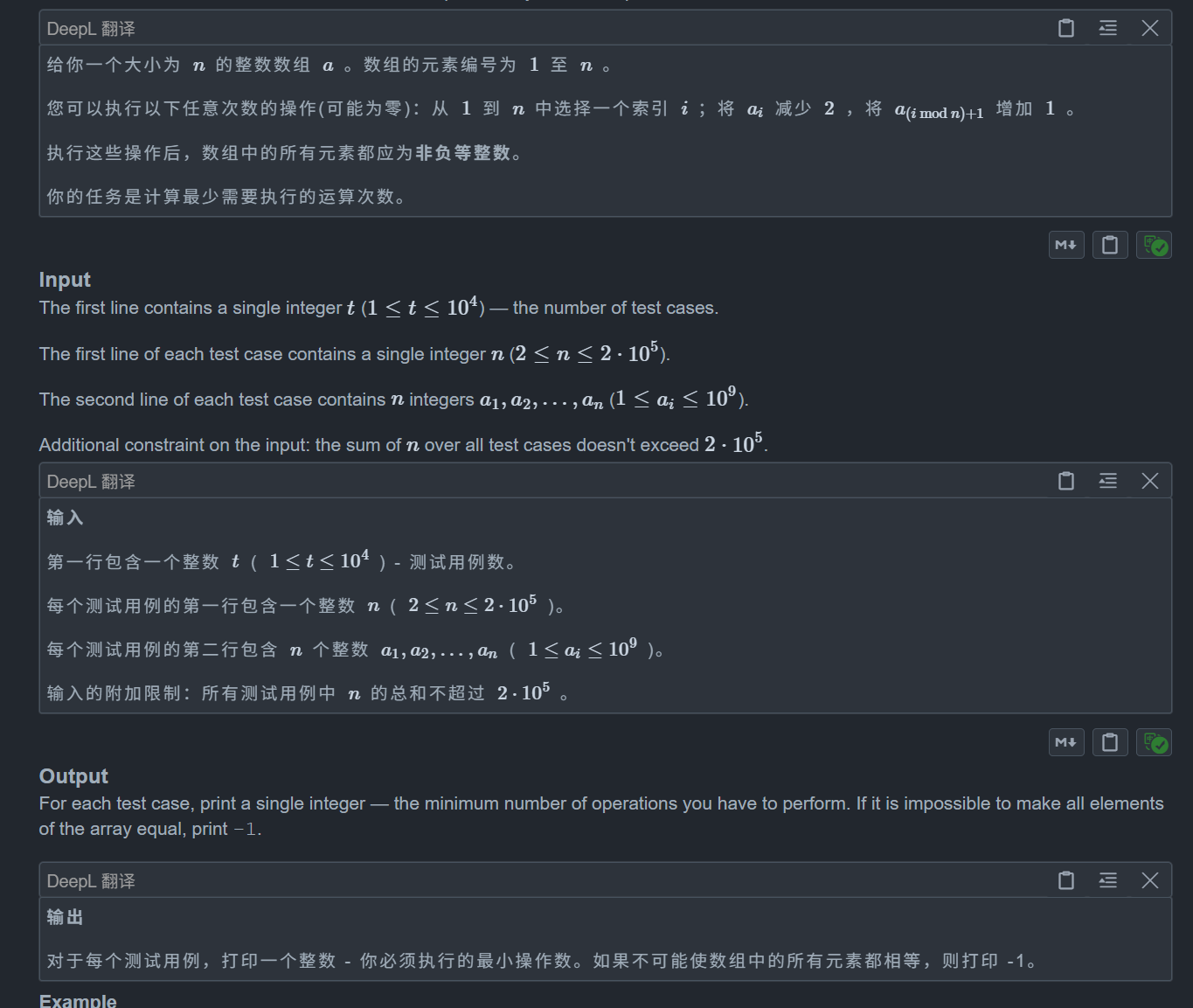
思路：

感觉很好，既能二分又能贪心

讲讲贪心思路吧，如果这个数组能够最后全一样，那么我们中间无论按什么样的操作顺序其实结果都一样，所以我们贪心的每次将能操作的全操作完，但是由于不能保证一次就成功，所以要多次操作，而对于每个数，其最多操作次数为 loga[i] 级别，因此整体为 nlogA，同时我们注意到如果 x 可以，那么 0 ~ x - 1 也都是可以的，因为我们可以操作所有的数一次，然后所有的数都会减少 1（这也是贪心和二分的关键点）

最后贪心的就是我们选取操作次数最少的那个数，然后将整体减去这次操作，由于操作具有可交换性，因此是可行的

对于二分做法，我们可以假设我们能操作到 mid，然后进行check，那么如何check呢？其实和上面大同小异，只不过这一次我们要有目的的操作，我们假设现在的数是 temp[i]，那么肯定就要操作 (temp[i] - mid) / 2 次，前提是 temp[i] > mid，否则不操作，同理一次可能也操作不完，所以也要多次操作，那么整体复杂度就是就是 nlog²A，也是可行的

代码：

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define yes cout << "YES\n"
#define no cout << "NO\n"
int b[200005];
void solve()
{int n;cin >> n;vector<int> a(n + 1, 0);for (int i = 1; i <= n; i++){cin >> a[i];b[i] = 0;}while (true){int used = 0;for (int i = 1; i <= n; i++){if (a[i] >= 2){b[i] += a[i] / 2;a[i % n + 1] += a[i] / 2;a[i] %= 2;used = 1;}}int allsame = 1;for (int i = 2; i <= n; i++){if (a[i] != a[i - 1]){allsame = 0;break;}}if (allsame)break;if (!used){cout << "-1\n";return;}}int sum = 0;int mi = 1e18;for (int i = 1; i <= n; i++){sum += b[i];mi = min(mi, b[i]);}cout << sum - mi * n << endl;
}signed main()
{ios::sync_with_stdio(false);cin.tie(nullptr);int t = 1;cin >> t;while (t--){solve();}return 0;
}

K. Grid Walk

题目：

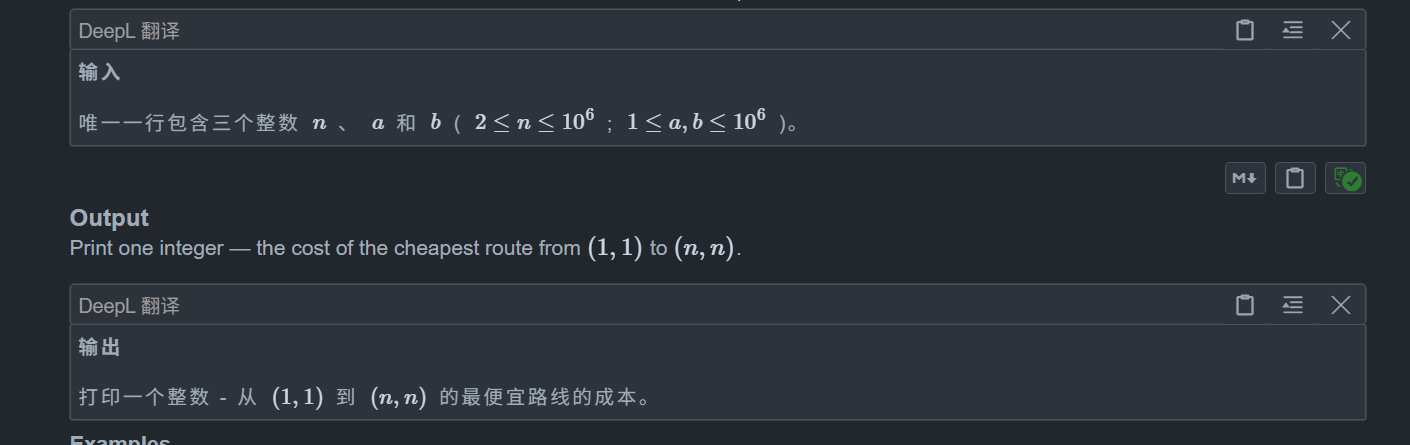思路：

绝美

我们注意到题目的答案很大，所以我们不能直接暴力使用 O(n²) 的dp，尝试考虑规律

我们发现 gcd(i, a) (i 属于 1 ~ n) 与 gcd(j, b) (j 属于 1 ~ n) 其实无论怎么走都会加上，那么就考虑如何让另一个 gcd 更小比较好，那么显然就是另一个 gcd = 1 是最好的

所以我们不妨考虑找到 gcd(i, a) = 1 的最大 i 和 gcd(j, b) = 1 的最大 j，令其风别为 A, B,那么显然如下图所示的走法是最优的

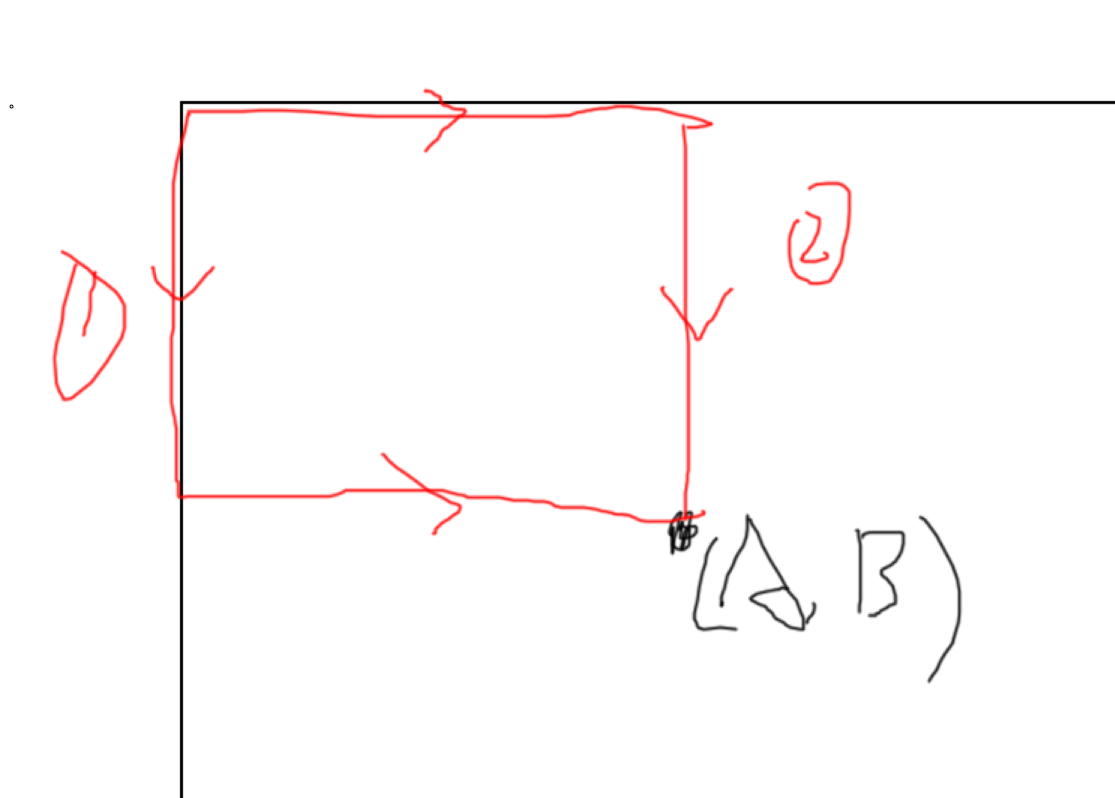
因为此时这两天边条边上全是 1 + 固定奉献，一定是最优的

那么对于之后的点怎么办呢？我们这里要找到一个性质，就是 n - A <= 25，n - B <= 25(最后证明)，当然其实我们可以先打表也行，因为 1e6 范围内的质数很密集，间隔也不是很大，最多 200 左右，这个暴力也是可以的

那么对于之后的点我们暴力转移即可，因为才 25 的大小，具体实现看代码，特别注意初始化答案要减去重复的奉献即可

来自luogu:CF2038K Grid Walk 解题报告 - 洛谷专栏

代码：

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define yes cout << "YES\n"
#define no cout << "NO\n"
int ga[1000005], gb[1000005];
void solve()
{int n, a, b;cin >> n >> a >> b;int A = 1, B = 1;for (int i = 1; i <= n; i++){ga[i] = gcd(i, a);if (ga[i] == 1){A = i;}}for (int i = 1; i <= n; i++){gb[i] = gcd(i, b);if (gb[i] == 1){B = i;}}int ans = A + B;for (int i = 2; i <= A; i++){ans += ga[i];}for (int i = 2; i <= B; i++){ans += gb[i];}int rn = n - A;int rm = n - B;vector<vector<int>> dp(50, vector<int>(50, 1e18));dp[0][0] = 0;for (int i = 0; i <= rn; i++){for (int j = 0; j <= rm; j++){if (i > 0)dp[i][j] = min(dp[i][j], dp[i - 1][j] + ga[A + i] + gb[B + j]);if (j > 0)dp[i][j] = min(dp[i][j], dp[i][j - 1] + ga[A + i] + gb[B + j]);}}cout << ans + dp[rn][rm] << endl;
}signed main()
{ios::sync_with_stdio(false);cin.tie(nullptr);int t = 1;while (t--){solve();}return 0;
}

查看全文

http://www.dtcms.com/a/331941.html