数据结构---关于复杂度的基础解析与梳理
目录
1.数据结构前言
1.1 数据结构是什么
1.2.算法
2.算法的复杂度
2.1.大O的渐进表示法
3.时间复杂度计算示例
3.1 案例1
3.2 案例2
3.3 案例3
4.复杂度的算法题
4.1 消失的数字
4.2 轮转数组
接下来我们就正式进入了数据结构的内容,首先我们来了解一下什么是数据结构和算法。
1.数据结构前言
1.1 数据结构是什么
数据结构(Data Structure)是计算机存储、组织数据的方式,指相互之间存在一种或多种特定关系的数据元素的集合。没有⼀种单一的数据结构对所有用途都有用,所以我们要学各式各样的数据结构,如:线性表、树、图、哈希等。
1.2.算法
算法(Algorithm):就是定义良好的计算过程,他取⼀个或⼀组的值为输入,并产生出一个或一组值作为输出。简单来说算法就是一系列的计算步骤,用来将输入数据转化成输出结果。
2.算法的复杂度
算法在编写成可执行程序时,运行需要消耗时间资源和内存资源,因此衡量一个算法的好坏,一般是从时间和空间两个角度衡量的,即时间复杂度和空间复杂度。
时间复杂度主要衡量一个算法的运行快慢,而空间复杂度主要衡量一个算法在运行时额外需要的空间,在计算机发展早期,计算机的存储容量很小,所以对空间复杂度比较在乎,现在计算机的存储容量已经非常巨大,所以我们现在对空间复杂度不是很在乎了,由此下面涉及到复杂度都是在说时间复杂度。
#include<stdio.h>
#include<time.h>int main(void)
{int begin1 = clock();//让clock记录循环开始前的时间点begin1int n = 100000000;int x = 10;for (int i = 0; i < n; ++i)//让变量i从0循环到一亿次{++x;//每次循环时对变量x进行自增操作(++x)}int end1 = clock();int begin2 = clock();int n1 = 1000000;for (int i = 0; i < n1; ++i){++x;}int end2 = clock();printf("%d\n", x);//输出经过这两段循环自增后x的最终值printf("%d ms\n", end1 - begin1);printf("%d ms\n", end2 - begin2);return 0;
}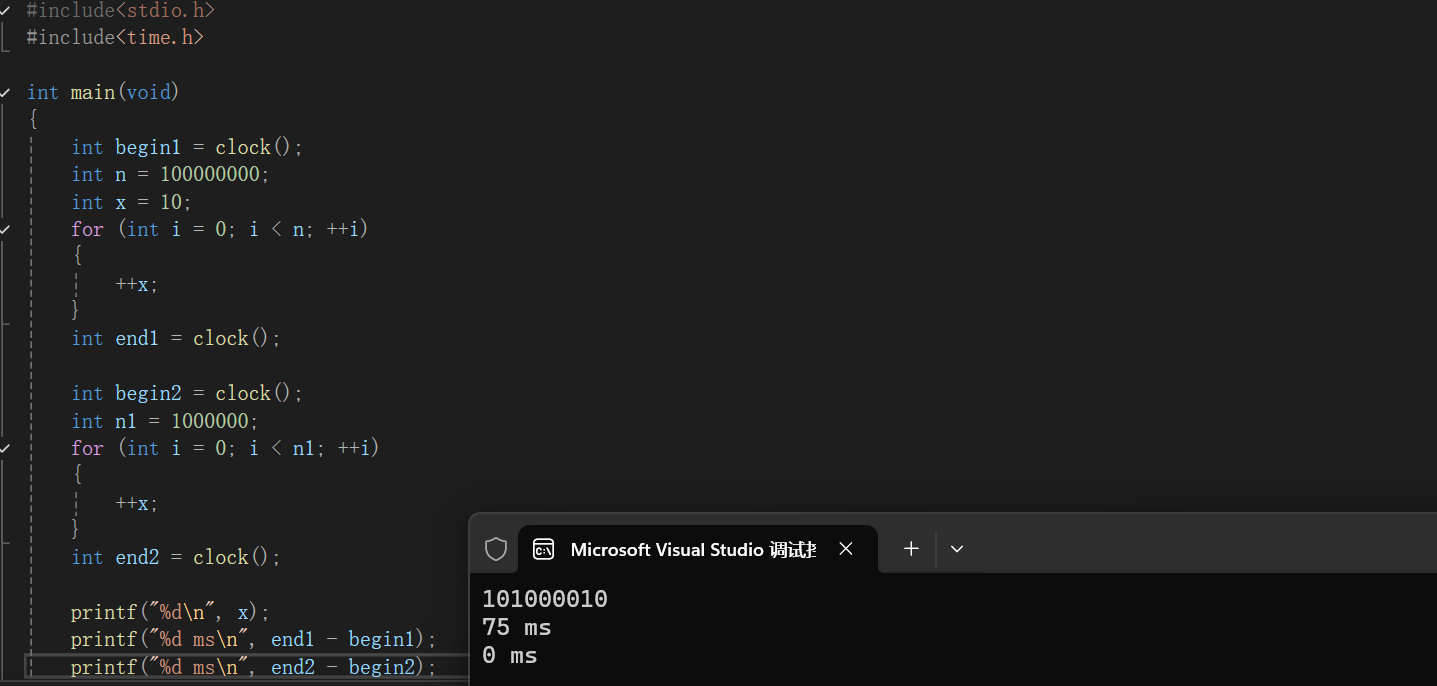
这段代码就是对比不同次数的循环执行时间,能帮助理解代码执行效率,和算法复杂度的直观体现相关,循环次数多的代码段通常花费的时间更长,对应的复杂度更高。
那么算法的时间复杂度是⼀个函数式T(N)到底是什么呢?这个T(N)函数式计算了程序的执行次数。通过c语⾔编译链接章节学习,我们知道算法程序被编译后生成⼆进制指令,程序运行,就是cpu执行这些编译好的指令。那么我们通过程序代码或者理论思想计算出程序的执行次数的函数式T(N),假设每句指令执行时间基本⼀样(实际中有差别,但是微乎其微),那么执行次数和运行时间就是等比正相关,这样也脱离了具体的编译运行环境。执行次数就可以代表程序时间效率的优劣。比如解决⼀个问题的算法a程序T(N) = N,算法b程序T(N) = N^2,那么算法a的效率⼀定优于算法b。
// 请计算⼀下Func1中++count语句总共执⾏了多少
次?
void Func1(int N)
{int count = 0;for (int i = 0; i < N ; ++ i){for (int j = 0; j < N ; ++ j){++count;}}for (int k = 0; k < 2 * N ; ++ k){++count;}int M = 10;while (M--){++count;}
}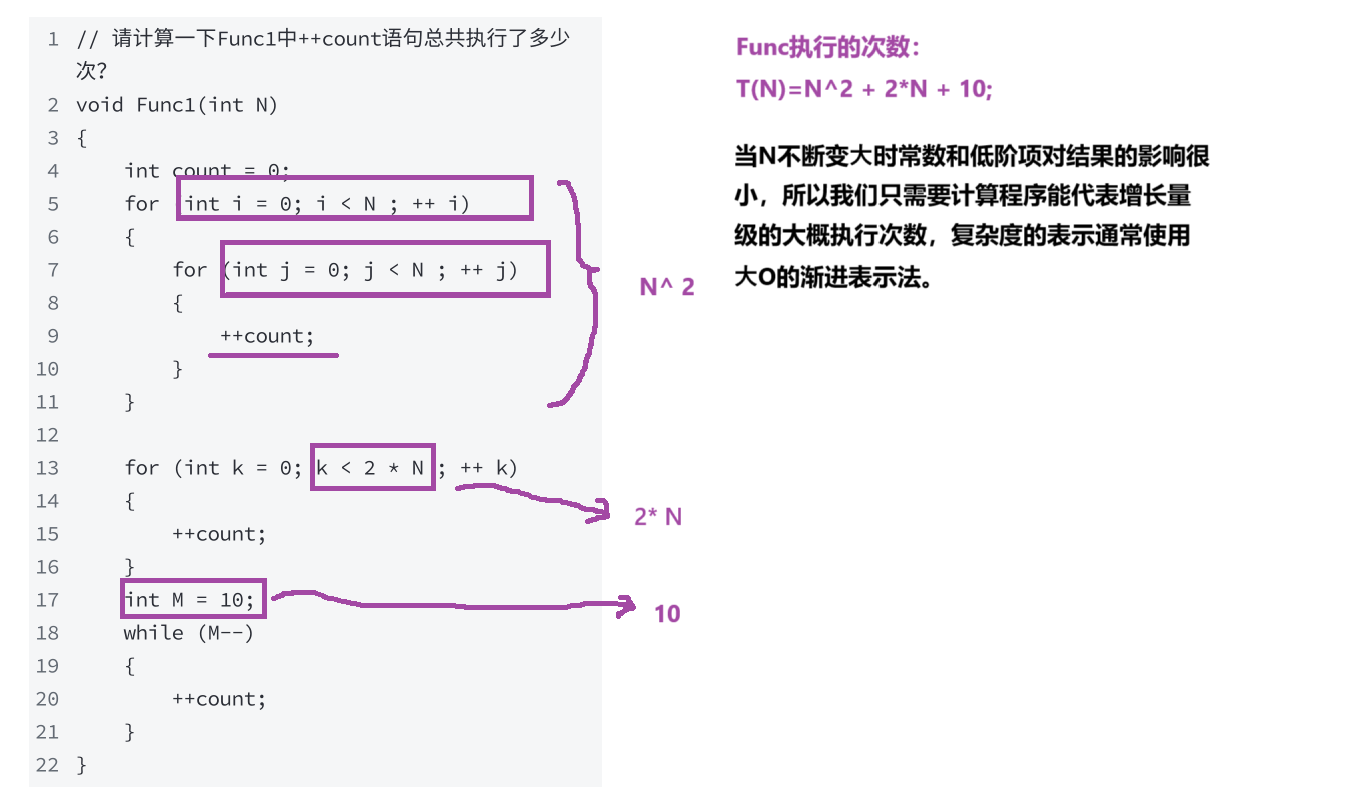
通过以上方法,可以得到 Func1 的时间复杂度为: O(N^2 )。
计算时间复杂度只是想比较算法程序的增长量级,也就是当N不断变大时T(N)的差别,上面我们已经看到了当N不断变大时常数和低阶项对结果的影响很小,所以我们只需要计算程序能代表增长量
级的大概执行次数,复杂度的表示通常使用大O的渐进表示法。
2.1.大O的渐进表示法
本质:计算算法时间复杂度(次数)属于哪个量级(level)。

3.时间复杂度计算示例
3.1 案例1
// 计算Func2的时间复杂度?
void Func2(int N)
{int count = 0;for (int k = 0; k < 2 * N ; ++ k){++count;}int M = 10;while (M--){++count;}printf("%d\n", count);
}
3.2 案例2
// 计算Func3的时间复杂度?
void Func3(int N, int M)
{int count = 0;for (int k = 0; k < M; ++ k){++count;}for (int k = 0; k < N ; ++k){++count;}printf("%d\n", count);
}
3.3 案例3
// 计算Func4的时间复杂度?
void Func4(int N)
{int count = 0;for (int k = 0; k < 100; ++ k){++count;}printf("%d\n", count);
}
通过上面我们会发现,有些算法的时间复杂度存在最好、平均和最坏情况。
最坏情况:任意输入规模的最大运行次数(上界)
平均情况:任意输入规模的期望运行次数
最好情况:任意输入规模的最小运行次数(下界)
大O的渐进表示法在实际中一般情况关注的是算法的上界,也就是最坏运行情况。
常见复杂度如下:
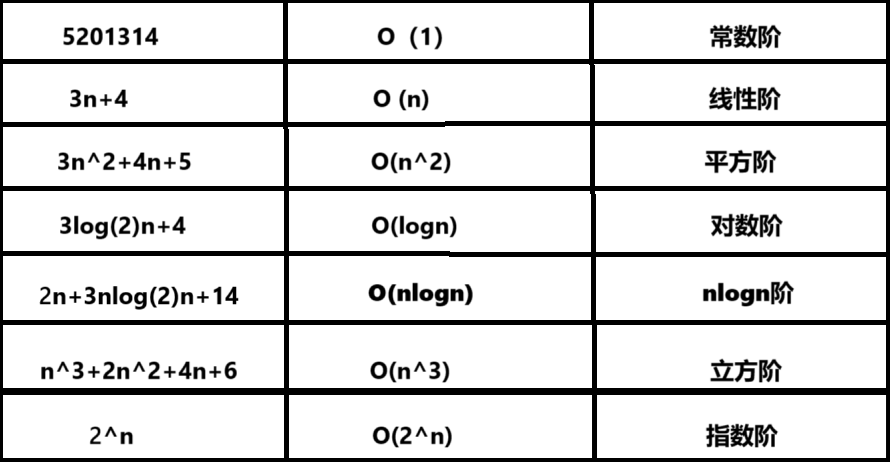
4.复杂度的算法题
4.1 消失的数字


思路二代码详解:
int missingNumber(int* nums, int numsSize) {int N=numsSize;int ret=(0+N)*(N+1)/2;//等差数列求所有数的和for(int i=0;i<N;++i){ret-=nums[i];//ret减等下标为所有项数,最后剩一个数字就是消失的数字}return ret;
}思路三代码详解:
int missingNumber(int* nums, int numsSize)
//两个参数,一个指向数组的首地址,一个表示数组的大小
{int x=0;//x用于通过异或来找出消失的数字for(int i=0;i<numsSize;i++)//第一次异或就是将数组中所有的元素与x进行异或{x^=nums[i];//每次循环的时候将x与数组nums中的第i个元素进行异或运算,相同的数字异或为0,不相同的数字异或不为0}for(int j=0;j<=numsSize;j++)//第二次异或就是将numsSize-1到0跟x进行异或{x^=j;//循环变量j从0开始,到numsSize-1结束}return x;
}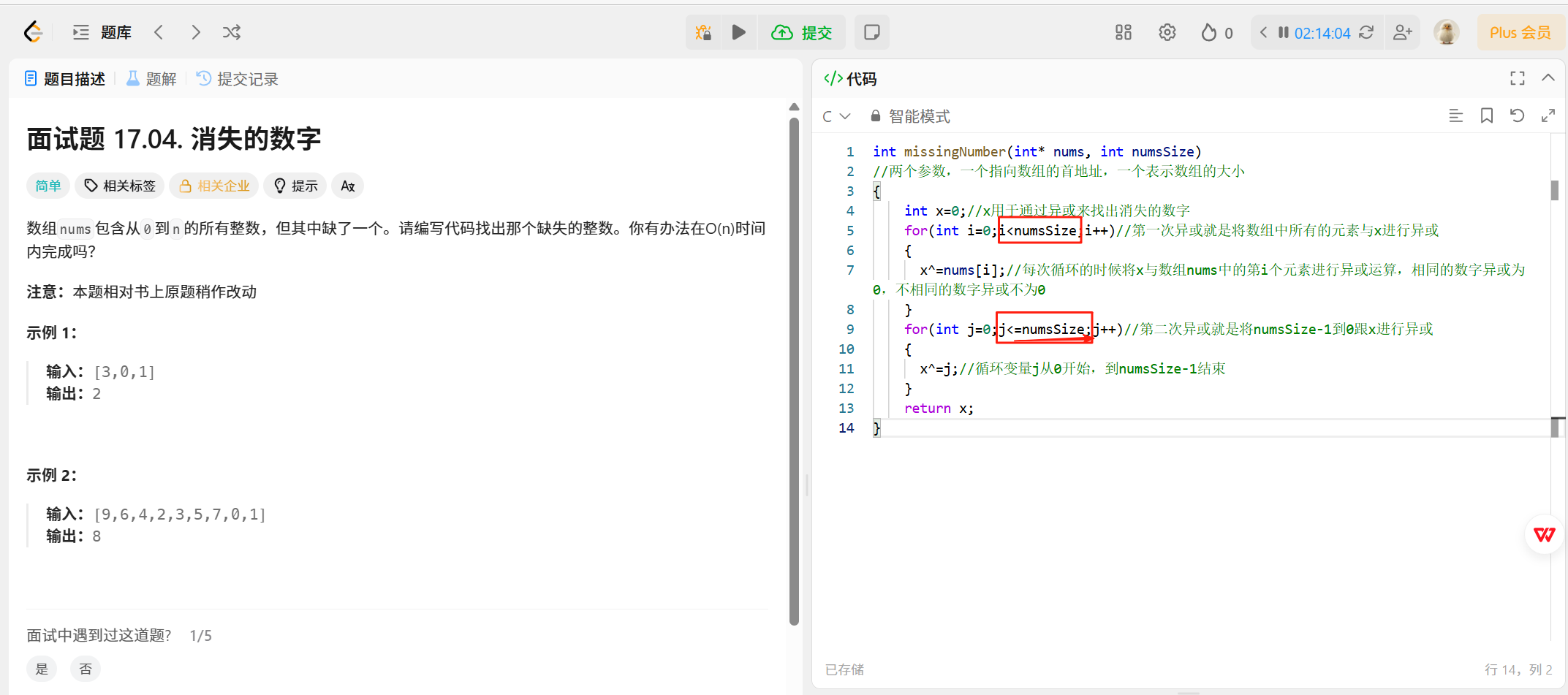
解释为什么上面的i后面没有=,但是下面的j后面要加=呢?
因为第一次异或的时候是将数组中所有元素都跟x=0异或,i是作为数组的下标用的。比如说,[0,1,3],numSize是3, 数组下标最大是2。--->用i取到数组的每个元素
第二次异或的时候是将数组本应该有的元素从0到numsSize-1都跟x=0进行异或,j是作为数据用的。数据是0,1,2, 3 ----->用j 访问这些数据
4.2 轮转数组


//思路一
void rotate(int* nums, int numsSize, int k) {k%=numsSize;while(k--) //当循环到k次{//旋转一次int tmp=nums[numsSize-1];//定义一个tmp,并将数组的最后一个元素下标为numsSize-1赋值给tmp,用于存储最后一个元素,因为后续移动元素会覆盖最后一个元素的位置for(int i=numsSize-2;i>=0;i--)//从数组的倒数第二个元素开始到第一个元素结束{nums[i+1]=nums[i];//将下标为i的元素赋值给i+1的位置}nums[0]=tmp;//将之前存储的最后一个元素tmp放到数组的开头,完成一次右旋转}
}//思路二
void reverse(int* nums,int left,int right)
{while(left<right){int tmp=nums[left];nums[left]=nums[right];nums[right]=tmp;left++;right--;}
}
void rotate(int* nums, int numsSize, int k) {k%= numsSize;reverse(nums,0,numsSize-k-1);//逆置前n-kreverse(nums,numsSize-k,numsSize-1);//后k个逆置reverse(nums,0,numsSize-1);//整体逆置
}logN的由来解释

因为写的时候需要专业的公式支持,否则不好写底数。
时间复杂度当中,为了方便,log N (以2为底N的对数)可以省略底数,直接写成logN,
其他底层不能省略(其他底数也很少出现)。
