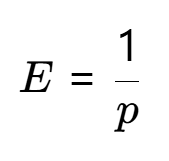用不均匀硬币实现公平决策
题目内容
有一个硬币不均匀,正面朝上70%,反面朝上30%。现在我们2个人出去吃饭,希望通过这枚硬币公平决策出谁买单,该如何决策?平均抛多少次可以决策出?
决策方法
这是一个关于利用不均匀硬币实现公平决策的概率问题。
抛掷硬币两次,按以下规则决定:
- 第一次正第二次反(概率0.7×0.3=0.21):A赢
- 第一次反第二次正(概率0.3×0.7=0.21):B赢
- 其他情况(概率1-0.42=0.58):重新抛
这样设计保证了双方获胜概率均为21%,完全公平。
期望抛掷次数计算:
设期望次数为E,建立方程:E = 0.42×2(成功) + 0.58×(2+E)(需要重抛)
展开得:E = 0.84 + 1.16 + 0.58E
移项得:0.42E = 2
解得:E ≈ 4.76次推导验证:
每次尝试需要抛2次,成功率42%
期望尝试次数 = 1/0.42 ≈ 2.38次
因此总期望次数 = 2.38×2 ≈ 4.76次
这个方案巧妙地利用两次抛掷的排列组合,抵消了硬币的不均匀性,实现了公平决策。
进一步解释
期望次数是什么意思?
期望次数(Expected Number of Trials)是指在概率问题中,为了达到某个目标(如成功决策谁买单),平均需要进行的尝试次数。它是一个长期统计的平均值,而不是某一次具体实验的结果。
为什么需要计算期望次数?
在这个问题中,由于硬币不均匀(正70%,反30%),直接抛一次会导致决策不公平。因此,我们采用抛两次硬币的策略:
- 正反(P=0.7×0.3=0.21) → A赢
- 反正(P=0.3×0.7=0.21) → B赢
- 正正或反反(P=0.7²+0.3²=0.58) → 重新抛
由于每次尝试(抛两次)有 42% 的成功概率(0.21+0.21),所以平均需要 1/0.42 ≈ 2.38 次尝试才能成功决策。
而每次尝试需要抛 2 次硬币,因此 期望总抛掷次数 ≈ 2.38 × 2 ≈ 4.76 次。
数学推导
设期望次数为 E,则:
- 成功(42%概率) → 只需抛 2 次
- 失败(58%概率) → 已经抛了 2 次,仍需再抛 E 次
因此,建立方程:E=0.42×2+0.58×(2+E)
解得:E=4.76 次
总结
- 期望次数 ≈ 4.76 次,表示长期来看,平均需要抛 4.76 次硬币才能公平决定谁买单。
- 期望(Expected Value)是概率论中的核心概念,用于衡量长期实验的平均结果。
什么是“期望”(Expected Value)?
“期望”是概率论中的一个核心概念,表示在长期重复实验中,某个随机事件的平均结果。你可以把它理解成“数学上的长期平均值”。
举个简单例子:掷骰子
假设你有一个公平的6面骰子,每个面(1~6)出现的概率都是 1/6。
那么,点数的期望值就是:
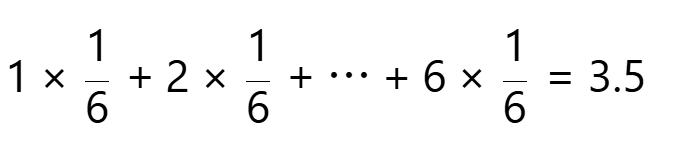
这意味着,如果你无限次掷骰子,最终所有点数的平均值会趋近于3.5(尽管你永远掷不出3.5点)。
回到硬币问题
在硬币问题中,我们计算的是“期望抛掷次数”,即:
- 每次尝试:抛2次硬币(可能成功,也可能失败需要重抛)。
- 成功概率:42%(即0.21+0.21)。
- 失败概率:58%(即0.7²+0.3²)。
数学推导:
设期望次数为 E,则:
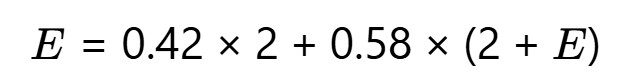
- 0.42×2:42%的概率只需抛2次就成功。
- 0.58×(2+E):58%的概率抛了2次后,仍需再抛E次。
解方程得:E=4.76 次
这意味着,长期来看,平均需要抛4.76次硬币才能公平决定谁买单。
关键点总结
- 期望 ≠ 单次结果:它描述的是长期趋势,不是某一次实验的结果。
- 加权平均:期望是所有可能结果的概率加权平均。
- 应用场景:在赌博、保险、投资、游戏设计等领域,期望值帮助人们预测长期收益或成本。
简单记忆:
“期望就是无限次重复实验后,统计出来的平均结果。”
另一种理解方式
1. 问题核心:如何用“作弊硬币”公平二选一?
- 你有一枚“作弊硬币”,正面70%,反面30%。
- 想用它公平决定谁买单(两人概率必须严格50%对50%)。
- 直接抛一次不行!(因为70%对30%不公平)
2. 解决方案:抛两次,看顺序
- 规则:
- 第一次正,第二次反(正反)→ 你赢
- 第一次反,第二次正(反正)→ 对方赢
- 其他情况(正正或反反)→ 重抛
为什么公平?
- 正反的概率 = 0.7×0.3 = 0.21
- 反正的概率 = 0.3×0.7 = 0.21
- 两人赢的概率完全相同(都是21%),剩下58%的情况无效。
3. 为什么平均要抛4.76次?
- 每次尝试:抛2次硬币。
- 成功率:42%(即21%+21%)。
- 失败率:58%(需要重抛)。
计算逻辑:
- 平均需要 1/0.42 ≈ 2.38次尝试才能成功一次。
- 每次尝试抛2次,所以总次数 = 2.38 × 2 ≈ 4.76次。
经典的“几何分布”问题:如果每次尝试的成功概率是 p,那么平均需要 1/p 次尝试才能成功一次。
- 可以理解为:成功概率是 42%,相当于平均每 100 次尝试能成功 42 次。
- 反过来,成功一次需要的平均尝试次数 = 100/42 ≈ 2.38 次。
在概率论中,这种“重复尝试直到成功”的问题属于几何分布。
几何分布的期望(平均尝试次数)公式为:其中,p 是单次尝试的成功概率(这里 p=0.42)。
通俗类比:
就像抽奖,中奖概率42%,平均抽2.38次能中一次。
但每次抽奖要花2块钱(抛2次),所以总成本是4.76块钱。
类似问题😊
题目:
有一个六面骰子,其中1点朝上的概率是30%,2点朝上的概率是20%,3、4、5、6点朝上的概率均为12.5%。现在Alice和Bob希望通过掷这个骰子公平地决定谁洗碗(即两人被选中的概率完全相等)。请设计一个方法,并计算平均需要掷多少次骰子才能做出决定。
提示:
类似于不均匀硬币的问题,可以考虑掷骰子的某些特定序列。
需要找到两个或多个序列,它们的概率相等,且可以分别对应Alice和Bob。
其他序列需要被忽略并重掷。
方法1(通用但低效):
连续掷骰子两次:
如果结果是(1,2),Alice洗碗。P(Alice) = P(1,2) = 0.06
如果结果是(2,1),Bob洗碗。P(Bob) = P(2,1) = 0.06
其他结果忽略并重掷。其他结果的概率 = 1 - 0.06 - 0.06 = 0.88
公平性:P(Alice) = P(Bob) =6%。
每次“尝试”是连续掷两次骰子:
成功概率((1,2)或(2,1)):P(成功) = 0.06 + 0.06 = 0.12
失败概率(其他结果):P(失败) = 1 - 0.12 = 0.88
期望尝试次数 = 1 / P(成功) = 1 / 0.12 ≈ 8.33次尝试
每次尝试掷骰2次,因此期望掷骰次数 = 8.33 × 2 ≈ 16.67次
方法2(高效但部分结果未利用):
P(3)=P(4)=P(5)=P(6)=0.125
掷骰子一次:
如果结果是3或4,Alice洗碗。P(Alice) = P(3) + P(4) = 0.125 + 0.125 = 0.25
如果结果是5或6,Bob洗碗。P(Bob) = P(5) + P(6) = 0.125 + 0.125 = 0.25
如果是1或2,忽略并重掷。忽略概率 = P(1) + P(2) = 0.3 + 0.2 = 0.5
公平性:P(Alice) = P(Bob) = 50%。
期望掷骰次数:
成功概率 = 0.25 + 0.25 = 0.5,失败概率 = 0.5
期望尝试次数 = 1 / 0.5 = 2次
每次尝试掷骰1次,因此E = 2 × 1 = 2次
推荐方法2,因为效率更高!