当前位置：首页 > news >正文

【YOLO系列】YOLOv1详解：模型结构、损失函数、训练方法及代码实现

news 2025/7/28 8:56:44

YOLOv1（You Only Look Once）：实时目标检测的革命性突破

✨ motivation

在目标检测领域，传统方法如R-CNN系列存在计算冗余、推理速度慢的问题。2016年提出的YOLO（You Only Look Once）首次实现端到端单阶段检测，将检测速度提升至45 FPS（Faster R-CNN仅7 FPS），彻底改变了实时目标检测的格局。其核心思想是将检测视为回归问题，实现"看一眼即知全貌"的突破。

📊 数据处理

采用PASCAL VOC 2007+2012数据集：

图像预处理：统一缩放至 $448 \times 448$ ，RGB三通道归一化
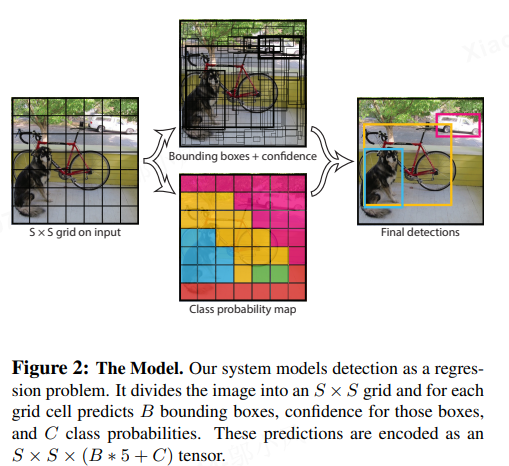
标签编码：将真值框编码为 $\times S \times (B \times 5 + C)$ 张量
其中 $S = 7$ （网格数）， $B = 2$ （每个网格预测框数）， $C = 20$ （类别数）
数据增强：随机缩放（±20%）、平移（最大偏移0.2倍图像尺寸）、HSV色彩扰动

🧠 模型结构

YOLOv1（You Only Look Once）是一种实时目标检测模型，由Joseph Redmon等人在2015年提出。其核心思想是将目标检测视为一个回归问题，一次性预测图像中的边界框（bounding boxes）和类别概率。相比于传统的两阶段检测器（如R-CNN），YOLOv1具有速度快、端到端训练的优势。下面我将详细介绍其模型结构，分步解释关键组件。
在这里插入图片描述

1. 整体架构概述

YOLOv1基于卷积神经网络（CNN），采用了一种简化的架构，类似于GoogLeNet，但针对目标检测任务进行了优化。模型输入为固定尺寸的图像（通常为448×448像素），输出是一个7×7的网格张量。每个网格单元负责预测多个边界框和类别信息。整个网络由24个卷积层和2个全连接层组成，结构紧凑，便于实时推理。
在这里插入图片描述

2. 网络层结构详解

YOLOv1的CNN部分主要用于特征提取，其层级结构如下：

卷积层：前20层使用卷积操作提取图像特征。这些层包括：
- 多个卷积块，每个块包含卷积、激活（ReLU）和池化操作。
- 卷积核尺寸逐渐减小，从7×7到3×3，以捕获多尺度特征。
- 使用步长（stride）和填充（padding）控制特征图尺寸。
全连接层：最后2层是全连接层，用于将特征图展平并生成最终预测。
- 第一全连接层：将特征图转换为4096维向量。
- 第二全连接层：输出7×7×30的张量（即1470维），这是模型的最终输出。

网络参数总结：

输入尺寸：448×448×3（RGB图像）。
输出尺寸：7×7×30（张量）。
总参数量：约45百万，模型轻量，适合实时应用。

3. 输出张量解释

YOLOv1的输出是一个7×7×30的三维张量，其中：

7×7网格：将输入图像划分为7×7的网格单元（grid cell）。每个单元对应图像中的一个区域（约64×64像素），负责检测中心点落在该区域的目标。
每个网格单元的预测：包含两部分：
- 边界框预测：每个网格单元预测2个边界框（bounding boxes）。每个边界框由5个值表示：
  - 中心坐标 $(x, y)$ ：相对于网格单元的相对位置，范围在[0,1]。
  - 宽度 $w$ 和高度 $h$ ：相对于整个图像的尺寸，归一化到[0,1]。
  - 置信度（confidence score）：表示该框包含目标的可能性，定义为 $P(object)×IOUP(\text{object}) \times \text{IOU}$ ，其中IOU（交并比）是预测框与真实框的重叠度。数学上，置信度公式为：
    $\text{confidence} = P(\text{object}) \cdot \text{IOU}_{\text{pred}}^{\text{truth}}$
    这里， $P(object)P(\text{object})$ 是目标存在的概率， $IOUpredtruth\text{IOU}_{\text{pred}}^{\text{truth}}$ 是预测框与真实框的IOU。
- 类别概率预测：每个网格单元预测20个类别的条件概率（基于PASCAL VOC数据集）。条件概率表示为 $P(classi∣object)P(\text{class}_i | \text{object})$ ，即在目标存在的前提下，该目标属于类别 $i$ 的概率。

因此，每个网格单元的输出维度为：2个框 × 5个值（x,y,w,h,confidence） + 20个类别概率 = 30维。整个输出张量可表示为：
$\text{输出} \in \mathbb{R}^{7 \times 7 \times 30}$

4. 预测机制工作流程

YOLOv1的预测过程分为三步：

图像划分：输入图像被划分为7×7网格。每个网格单元独立处理局部特征。
边界框生成：对于每个网格单元，模型预测2个边界框。这些框通过非极大值抑制（NMS）后处理去除冗余，保留置信度最高的框。
类别分配：每个网格单元计算类别概率分布。最终检测时，边界框的类别由网格单元的类别概率和置信度共同决定：
- 具体公式：某个边界框属于类别 $i$ 的得分为：
  $\text{score}_i = P(\text{class}_i | \text{object}) \times \text{confidence}$
  得分最高的类别被分配给该框。

5. 优势与局限性总结

YOLOv1的结构简单高效，实现了端到端训练，推理速度快（可达45帧/秒）。然而，其网格划分机制可能导致小目标检测精度较低，因为每个网格单元仅预测固定数量的框。后续版本（如YOLOv2/v3）通过改进锚框（anchor boxes）和多尺度预测优化了这些不足。

⚖️ 损失函数

YOLOv1损失函数详细介绍

YOLOv1（You Only Look Once version 1）是一种单阶段目标检测模型，其核心创新是将目标检测视为一个回归问题，直接在图像网格上预测边界框（bounding box）和类别概率。损失函数的设计是YOLOv1的关键，它通过加权组合多个误差项来平衡位置、置信度和分类任务，确保模型高效训练。损失函数采用平方误差（Sum-Squared Error）形式，因为它易于优化，但通过权重系数解决了不同任务间的不平衡问题。下面我将逐步分解YOLOv1损失函数的各个部分。

损失函数总体结构

YOLOv1损失函数是一个加权和，包含五个主要部分：

位置损失：用于预测边界框的坐标（中心点 $x, y$ 和尺寸 $w, h$ ）。
置信度损失：用于预测边界框是否包含对象（objectness）。
分类损失：用于预测对象所属类别。

整体损失函数公式如下：
$L_{\text{coord}} + L_{\text{conf}} + L_{\text{class}}$
其中：

$LcoordL_{\text{coord}}$ 是位置损失。
$LconfL_{\text{conf}}$ 是置信度损失。
$LclassL_{\text{class}}$ 是分类损失。

每个部分都涉及权重系数和指示函数，以处理不同情况（如有对象或无对象）。YOLOv1将图像划分为 $\times S$ 网格（通常 $S = 7$ ），每个网格单元预测 $B$ 个边界框（通常 $B = 2$ ）。下面详细解释每个组件。

1. 位置损失（ $LcoordL_{\text{coord}}$ ）

位置损失负责优化边界框的坐标预测，包括中心点 $(x, y)$ 和尺寸 $(w, h)$ 。为了平衡不同尺寸边界框的误差，YOLOv1对宽度和高度使用平方根变换，以减少大尺寸框的误差影响。位置损失仅应用于“负责”检测对象的边界框（即与真实框IoU最高的预测框）。

公式：
$Lcoord=λcoord∑i=0S2∑j=0B1ijobj[(xi−x^i)2+(yi−y^i)2]+λcoord∑i=0S2∑j=0B1ijobj[(wi−w^i)2+(hi−h^i)2]L_{\text{coord}} = \lambda_{\text{coord}} \sum_{i=0}^{S^2} \sum_{j=0}^{B} \mathbb{1}_{ij}^{\text{obj}} \left[ (x_i - \hat{x}_i)^2 + (y_i - \hat{y}_i)^2 \right] + \lambda_{\text{coord}} \sum_{i=0}^{S^2} \sum_{j=0}^{B} \mathbb{1}_{ij}^{\text{obj}} \left[ (\sqrt{w_i} - \sqrt{\hat{w}_i})^2 + (\sqrt{h_i} - \sqrt{\hat{h}_i})^2 \right]$

其中：

$1ijobj\mathbb{1}_{ij}^{\text{obj}}$ 是指示函数，当第 $i$ 个网格单元的第 $j$ 个边界框负责检测对象时值为1（即该框与真实框的IoU最大），否则为0。
$x_i, y_i, w_i, h_i$ 是预测值。
$x^i,y^i,w^i,h^i\hat{x}_i, \hat{y}_i, \hat{w}_i, \hat{h}_i$ 是真实值（ground truth）。
$λcoord\lambda_{\text{coord}}$ 是位置损失的权重系数，通常设为5，以增强坐标误差的重要性（因为位置精度对检测任务至关重要）。

关键点：

中心点误差 $(xi−x^i)2+(yi−y^i)2(x_i - \hat{x}_i)^2 + (y_i - \hat{y}_i)^2$ 直接使用平方误差。
尺寸误差 $(wi−w^i)2+(hi−h^i)2(\sqrt{w_i} - \sqrt{\hat{w}_i})^2 + (\sqrt{h_i} - \sqrt{\hat{h}_i})^2$ 通过平方根处理，使得小尺寸框的误差更敏感（例如，预测 $w_i=10$ 和真实 $w^i=1\hat{w}_i=1$ 时，误差较大；而 $w_i=100$ 和 $w^i=91\hat{w}_i=91$ 时，误差较小）。

2. 置信度损失（ $LconfL_{\text{conf}}$ ）

置信度损失用于预测边界框的“对象存在概率”（即置信度分数 $C_i$ ，范围[0,1]）。它分为两部分：

有对象损失：当边界框负责检测对象时，优化置信度接近1。
无对象损失：当边界框不负责对象时，优化置信度接近0（减少负样本的影响）。

公式：
$Lconf=∑i=0S2∑j=0B1ijobj(Ci−C^i)2+λnoobj∑i=0S2∑j=0B1ijnoobj(Ci−C^i)2L_{\text{conf}} = \sum_{i=0}^{S^2} \sum_{j=0}^{B} \mathbb{1}_{ij}^{\text{obj}} (C_i - \hat{C}_i)^2 + \lambda_{\text{noobj}} \sum_{i=0}^{S^2} \sum_{j=0}^{B} \mathbb{1}_{ij}^{\text{noobj}} (C_i - \hat{C}_i)^2$

其中：

$1ijnoobj\mathbb{1}_{ij}^{\text{noobj}}$ 是指示函数，当第 $i$ 个网格单元的第 $j$ 个边界框不负责对象时值为1，否则为0（注意： $1ijnoobj=1−1ijobj\mathbb{1}_{ij}^{\text{noobj}} = 1 - \mathbb{1}_{ij}^{\text{obj}}$ ）。
$C_i$ 是预测置信度。
$C^i\hat{C}_i$ 是真实置信度（有对象时为1，无对象时为0）。
$λnoobj\lambda_{\text{noobj}}$ 是无对象损失的权重系数，通常设为0.5，以减少负样本的梯度影响（因为图像中大部分网格不包含对象）。

关键点：

第一项 $∑1ijobj(Ci−C^i)2\sum \mathbb{1}_{ij}^{\text{obj}} (C_i - \hat{C}_i)^2$ 强制有对象框的置信度接近1。
第二项 $λnoobj∑1ijnoobj(Ci−C^i)2\lambda_{\text{noobj}} \sum \mathbb{1}_{ij}^{\text{noobj}} (C_i - \hat{C}_i)^2$ 强制无对象框的置信度接近0，但权重较低（ $λnoobj=0.5\lambda_{\text{noobj}}=0.5$ ），避免无对象样本主导训练。

3. 分类损失（ $LclassL_{\text{class}}$ ）

分类损失用于预测对象所属类别概率。每个网格单元预测一个条件概率分布 $p(c∣object)p(c|\text{object})$ ，表示如果网格包含对象中心，则对象属于类别 $c$ 的概率。损失仅应用于包含对象中心的网格单元。

公式：
$Lclass=∑i=0S21iobj∑c=1C(pi(c)−p^i(c))2L_{\text{class}} = \sum_{i=0}^{S^2} \mathbb{1}_{i}^{\text{obj}} \sum_{c=1}^{C} (p_i(c) - \hat{p}_i(c))^2$

其中：

$1iobj\mathbb{1}_{i}^{\text{obj}}$ 是指示函数，当第 $i$ 个网格单元包含对象中心时值为1，否则为0。
$p_i(c)$ 是预测的第 $c$ 个类别的概率。
$p^i(c)\hat{p}_i(c)$ 是真实概率（one-hot编码，真实类别为1，其他为0）。
$C$ 是类别总数（如PASCAL VOC数据集有20类）。

关键点：

分类损失是平方误差，而非交叉熵，因为YOLOv1整体采用平方误差框架。
每个网格单元只预测一个类别分布（与边界框数 $B$ 无关），因此损失基于网格单元而非边界框。

权重系数的意义

$λcoord=5\lambda_{\text{coord}} = 5$ ：增加位置损失的权重，因为坐标误差对检测精度影响更大（例如，位置偏移可能导致误检）。
$λnoobj=0.5\lambda_{\text{noobj}} = 0.5$ ：降低无对象置信度损失的权重，因为图像中负样本（无对象区域）远多于正样本，防止负样本梯度淹没正样本。

损失函数特点总结

整体公式：结合上述部分，完整损失函数为：
$L=λcoord∑i=0S2∑j=0B1ijobj[(xi−x^i)2+(yi−y^i)2+(wi−w^i)2+(hi−h^i)2]+∑i=0S2∑j=0B1ijobj(Ci−C^i)2+λnoobj∑i=0S2∑j=0B1ijnoobj(Ci−C^i)2+∑i=0S21iobj∑c=1C(pi(c)−p^i(c))2L = \lambda_{\text{coord}} \sum_{i=0}^{S^2} \sum_{j=0}^{B} \mathbb{1}_{ij}^{\text{obj}} \left[ (x_i - \hat{x}_i)^2 + (y_i - \hat{y}_i)^2 + (\sqrt{w_i} - \sqrt{\hat{w}_i})^2 + (\sqrt{h_i} - \sqrt{\hat{h}_i})^2 \right] + \sum_{i=0}^{S^2} \sum_{j=0}^{B} \mathbb{1}_{ij}^{\text{obj}} (C_i - \hat{C}_i)^2 + \lambda_{\text{noobj}} \sum_{i=0}^{S^2} \sum_{j=0}^{B} \mathbb{1}_{ij}^{\text{noobj}} (C_i - \hat{C}_i)^2 + \sum_{i=0}^{S^2} \mathbb{1}_{i}^{\text{obj}} \sum_{c=1}^{C} (p_i(c) - \hat{p}_i(c))^2$
优点：通过权重平衡，解决了位置、置信度和分类任务的不平衡问题；平方误差简化了优化。
局限：平方误差对分类任务不是最优（后续版本如YOLOv2改用交叉熵），且对小对象检测不够鲁棒。

YOLOv1损失函数的设计体现了端到端回归的思想，使其在速度和精度上取得了平衡。训练时，该损失函数通过反向传播优化模型参数，实现高效的目标检测。

🚀 训练方法

优化器：SGD动量优化器（动量0.9）
学习率：分段衰减 $10^{-3} \to 10^{-2} \to 10^{-3} \to 10^{-4}$
批次大小：64
训练周期：135 epoch
正则化：Dropout (rate=0.5) + L2权重衰减(0.0005)

📈 实验效果

在PASCAL VOC 2007测试集：

指标	YOLOv1	Faster R-CNN
mAP	63.4%	70.0%
FPS	45	7
模型尺寸	约750MB	约1.2GB

核心优势：在保持 $AP_{50}$ 达88%的同时，推理速度提升6倍以上！

🔑 关键代码

以下展示YOLOv1的关键实现代码（基于PyTorch框架），包含模型架构和损失函数的核心部分：

import torch
import torch.nn as nnclass YOLOv1(nn.Module):def __init__(self, grid_size=7, num_boxes=2, num_classes=20):super().__init__()self.grid_size = grid_sizeself.num_boxes = num_boxesself.num_classes = num_classes# 特征提取网络（简化版，原文使用24层卷积）self.features = nn.Sequential(nn.Conv2d(3, 64, 7, stride=2, padding=3),nn.LeakyReLU(0.1),nn.MaxPool2d(2, stride=2),nn.Conv2d(64, 192, 3, padding=1),nn.LeakyReLU(0.1),nn.MaxPool2d(2, stride=2))# 检测头（输出层）self.detector = nn.Sequential(nn.Linear(192 * grid_size * grid_size, 4096),nn.LeakyReLU(0.1),nn.Linear(4096, grid_size * grid_size * (num_classes + num_boxes * 5)))def forward(self, x):x = self.features(x)x = torch.flatten(x, 1)x = self.detector(x)# 重塑为 [batch, S, S, (C + B*5)] 张量return x.view(-1, self.grid_size, self.grid_size, self.num_classes + 5 * self.num_boxes)

损失函数核心实现

def yolo_loss(preds, targets, lambda_coord=5, lambda_noobj=0.5):"""preds:  预测张量 [batch, S, S, C+B*5]targets: 标签张量 [batch, S, S, C+5]"""# 坐标损失权重coord_mask = targets[..., 20:21]  # 物体存在指示器noobj_mask = 1 - coord_mask# 边界框坐标损失box_pred = preds[..., 21:25]box_target = targets[..., 21:25]box_loss = lambda_coord * coord_mask * torch.sum((box_pred[..., :2] - box_target[..., :2])**2 + (torch.sqrt(box_pred[..., 2:4]) - torch.sqrt(box_target[..., 2:4]))**2,dim=-1)# 物体置信度损失conf_pred = preds[..., 20:21]conf_target = targets[..., 20:21]conf_loss = coord_mask * (conf_pred - conf_target)**2 + \lambda_noobj * noobj_mask * (conf_pred - conf_target)**2# 分类损失class_pred = preds[..., :20]class_target = targets[..., :20]class_loss = coord_mask * torch.sum((class_pred - class_target)**2, dim=-1)# 总损失total_loss = torch.sum(box_loss + conf_loss + class_loss)return total_loss