前缀和题目:元素和小于等于阈值的正方形的最大边长
文章目录
- 题目
- 标题和出处
- 难度
- 题目描述
- 要求
- 示例
- 数据范围
- 前言
- 解法
- 思路和算法
- 代码
- 复杂度分析
题目
标题和出处
标题:元素和小于等于阈值的正方形的最大边长
出处:1292. 元素和小于等于阈值的正方形的最大边长
难度
7 级
题目描述
要求
给定一个大小为 m×n\texttt{m} \times \texttt{n}m×n 的矩阵 mat\texttt{mat}mat 和一个整数 threshold\texttt{threshold}threshold,返回元素总和小于或等于 threshold\texttt{threshold}threshold 的正方形区域的最大边长,如果没有这样的正方形区域则返回 0\texttt{0}0。
示例
示例 1:
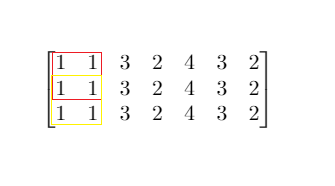
输入:mat=[[1,1,3,2,4,3,2],[1,1,3,2,4,3,2],[1,1,3,2,4,3,2]],threshold=4\texttt{mat = [[1,1,3,2,4,3,2],[1,1,3,2,4,3,2],[1,1,3,2,4,3,2]], threshold = 4}mat = [[1,1,3,2,4,3,2],[1,1,3,2,4,3,2],[1,1,3,2,4,3,2]], threshold = 4
输出:2\texttt{2}2
解释:总和小于或等于 4\texttt{4}4 的正方形的最大边长为 2\texttt{2}2,如图所示。
示例 2:
输入:mat=[[2,2,2,2,2],[2,2,2,2,2],[2,2,2,2,2],[2,2,2,2,2],[2,2,2,2,2]],threshold=1\texttt{mat = [[2,2,2,2,2],[2,2,2,2,2],[2,2,2,2,2],[2,2,2,2,2],[2,2,2,2,2]], threshold = 1}mat = [[2,2,2,2,2],[2,2,2,2,2],[2,2,2,2,2],[2,2,2,2,2],[2,2,2,2,2]], threshold = 1
输出:0\texttt{0}0
数据范围
- m=mat.length\texttt{m} = \texttt{mat.length}m=mat.length
- n=mat[i].length\texttt{n} = \texttt{mat[i].length}n=mat[i].length
- 1≤m,n≤300\texttt{1} \le \texttt{m, n} \le \texttt{300}1≤m, n≤300
- 0≤mat[i][j]≤104\texttt{0} \le \texttt{mat[i][j]} \le \texttt{10}^\texttt{4}0≤mat[i][j]≤104
- 0≤threshold≤105\texttt{0} \le \texttt{threshold} \le \texttt{10}^\texttt{5}0≤threshold≤105
前言
这道题要求返回矩阵 mat\textit{mat}mat 中的元素和不超过 threshold\textit{threshold}threshold 的正方形区域的最大边长。计算正方形区域的元素和需要通过二维前缀和实现,二维前缀和的实现可以使用「二维区域和检索 - 矩阵不可变」的做法。
解法
思路和算法
为了快速计算每个正方形区域的元素和,需要使用二维前缀和。
对于 m×nm \times nm×n 的矩阵 mat\textit{mat}mat,创建 (m+1)×(n+1)(m + 1) \times (n + 1)(m+1)×(n+1) 的前缀和矩阵 prefixSums\textit{prefixSums}prefixSums,对于 0≤i≤m0 \le i \le m0≤i≤m 和 0≤j≤n0 \le j \le n0≤j≤n,prefixSums[i][j]\textit{prefixSums}[i][j]prefixSums[i][j] 表示 mat\textit{mat}mat 的行数为 iii、列数为 jjj 的前缀和,即行下标范围 [0,i−1][0, i - 1][0,i−1]、列下标范围 [0,j−1][0, j - 1][0,j−1] 中的所有元素之和:
prefixSums[i][j]=∑0≤p<i,0≤q<jmat[p][q]\textit{prefixSums}[i][j] = \sum\limits_{0 \le p < i, 0 \le q < j} \textit{mat}[p][q] prefixSums[i][j]=0≤p<i,0≤q<j∑mat[p][q]
特别地,当 iii 和 jjj 中至少有一个值等于 000 时,prefixSums[i][j]=0\textit{prefixSums}[i][j] = 0prefixSums[i][j]=0。
对于 0≤i<m0 \le i < m0≤i<m 和 0≤j<n0 \le j < n0≤j<n,prefixSums[i+1][j+1]\textit{prefixSums}[i + 1][j + 1]prefixSums[i+1][j+1] 的值计算如下:
prefixSums[i+1][j+1]=prefixSums[i][j+1]+prefixSums[i+1][j]−prefixSums[i][j]+mat[i][j]\begin{aligned} &\textit{prefixSums}[i + 1][j + 1] \\ = &\textit{prefixSums}[i][j + 1] \\ &+ \textit{prefixSums}[i + 1][j] \\ &- \textit{prefixSums}[i][j] \\ &+ \textit{mat}[i][j] \end{aligned} =prefixSums[i+1][j+1]prefixSums[i][j+1]+prefixSums[i+1][j]−prefixSums[i][j]+mat[i][j]
得到前缀和矩阵 prefixSums\textit{prefixSums}prefixSums 之后,对于 0≤i<m0 \le i < m0≤i<m 和 0≤j<n0 \le j < n0≤j<n,当 side≤min(i+1,j+1)\textit{side} \le \min(i + 1, j + 1)side≤min(i+1,j+1) 时,以 (i,j)(i, j)(i,j) 为右下角且边长为 side\textit{side}side 的正方形区域的元素和为 prefixSums[i+1][j+1]−prefixSums[i+1−side][j+1]−prefixSums[i+1][j+1−side]+prefixSums[i+1−side][j+1−side]\textit{prefixSums}[i + 1][j + 1] - \textit{prefixSums}[i + 1 - \textit{side}][j + 1] - \textit{prefixSums}[i + 1][j + 1 - \textit{side}] + \textit{prefixSums}[i + 1 - \textit{side}][j + 1 - \textit{side}]prefixSums[i+1][j+1]−prefixSums[i+1−side][j+1]−prefixSums[i+1][j+1−side]+prefixSums[i+1−side][j+1−side]。
用 maxSide\textit{maxSide}maxSide 表示元素和小于等于 threshold\textit{threshold}threshold 的的正方形区域的最大边长,初始时 maxSide=0\textit{maxSide} = 0maxSide=0。从上到下、从左到右依次遍历矩阵 mat\textit{mat}mat 的每个元素,对于每个行下标 iii 和列下标 jjj,执行如下操作。
-
计算以当前位置为右下角的前缀和 prefixSums[i+1][j+1]\textit{prefixSums}[i + 1][j + 1]prefixSums[i+1][j+1]。
-
令 side=maxSide+1\textit{side} = \textit{maxSide} + 1side=maxSide+1,如果以 (i,j)(i, j)(i,j) 为右下角且边长为 side\textit{side}side 的正方形区域存在且该正方形区域的元素和小于等于 threshold\textit{threshold}threshold,则用 side\textit{side}side 更新 maxSide\textit{maxSide}maxSide,然后将 side\textit{side}side 加 111。重复该操作,直到以 (i,j)(i, j)(i,j) 为右下角且边长为 side\textit{side}side 的正方形区域不存在或该正方形区域的元素和大于 threshold\textit{threshold}threshold。
当遍历到位置 (i,j)(i, j)(i,j) 时,如果 maxSide\textit{maxSide}maxSide 的值更新,则当 maxSide\textit{maxSide}maxSide 更新结束时,一定存在以当前位置为右下角且边长为 maxSide\textit{maxSide}maxSide 的正方形区域的元素和小于等于 threshold\textit{threshold}threshold,且不存在以当前位置为右下角且边长为 maxSide+1\textit{maxSide} + 1maxSide+1 的正方形区域的元素和小于等于 threshold\textit{threshold}threshold。因此上述操作可以得到正确的结果。
由于在遍历矩阵的过程中,maxSide\textit{maxSide}maxSide 的值只会增加,且不会超过矩阵的行数和列数,因此 maxSide\textit{maxSide}maxSide 的总更新次数不会超过 min(m,n)\min(m, n)min(m,n)。
代码
class Solution {public int maxSideLength(int[][] mat, int threshold) {int maxSide = 0;int m = mat.length, n = mat[0].length;int[][] prefixSums = new int[m + 1][n + 1];for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {prefixSums[i + 1][j + 1] = prefixSums[i][j + 1] + prefixSums[i + 1][j] - prefixSums[i][j] + mat[i][j];int side = maxSide + 1;while (i + 1 - side >= 0 && j + 1 - side >= 0 && squareSum(prefixSums, i, j, side) <= threshold) {maxSide = side;side++;}}}return maxSide;}public int squareSum(int[][] prefixSums, int row, int col, int side) {return prefixSums[row + 1][col + 1] - prefixSums[row + 1 - side][col + 1] - prefixSums[row + 1][col + 1 - side] + prefixSums[row + 1 - side][col + 1 - side];}
}
复杂度分析
-
时间复杂度:O(m×n)O(m \times n)O(m×n),其中 mmm 和 nnn 分别是矩阵 mat\textit{mat}mat 的行数和列数。需要遍历矩阵一次,对于矩阵中的每个元素,计算前缀和、计算正方形区域的元素和以及更新正方形的最大边长的时间都是 O(1)O(1)O(1),且正方形的最大边长最多更新 min(m,n)\min(m, n)min(m,n) 次,因此时间复杂度是 O(m×n+min(m,n))=O(m×n)O(m \times n + \min(m, n)) = O(m \times n)O(m×n+min(m,n))=O(m×n)。
-
空间复杂度:O(m×n)O(m \times n)O(m×n),其中 mmm 和 nnn 分别是矩阵 mat\textit{mat}mat 的行数和列数。需要创建 (m+1)×(n+1)(m + 1) \times (n + 1)(m+1)×(n+1) 的前缀和矩阵。
