2024年ASOC SCI2区TOP,基于Jaya算法的粒子滤波器用于非线性模型贝叶斯更新,深度解析+性能实测
目录
- 1.摘要
- 2.Jaya算法原理
- 3.理论背景
- 4.PF-JAYA算法
- 5.结果展示
- 6.参考文献
- 7.算法辅导·应用定制·读者交流

1.摘要
粒子滤波器(PF)是一种常用的非线性系统状态和参数估计方法,但在实际应用中容易出现粒子退化和粒子贫乏的问题,尤其是在粒子数量有限的情况下,会影响估计精度。因此,本文提出了一种Jaya优化算法与粒子滤波器的混合方法(PF-JAYA),用于岩土工程中的状态与参数联合估计。研究结果表明,PF-JAYA在准确性、收敛速度、参数识别和粒子多样性等方面均优于传统的采样重要性重采样粒子滤波器(PF-SIR),且对先验分布的选择不敏感,能更好适应监测信息稀少的情形。
2.Jaya算法原理
【智能算法】JAYA算法原理及实现
3.理论背景
粒子滤波
粒子滤波器(PF) 是一种常用于解决非线性和高维系统的贝叶斯更新问题的方法。系统状态xkx_kxk由前向模型驱动,并通过观测值yky_kyk被观测。系统的状态演化由下式描述,
xk=F(xk−1)+qk−1yk=Hk(xk)+vk\begin{aligned} x_k & =F(x_{k-1})+q_{k-1} \\ y_k & =H_k(x_k)+v_k \end{aligned} xkyk=F(xk−1)+qk−1=Hk(xk)+vk
并通过观测方程与噪声进行耦合。通过所有可用的观测值,系统的状态在每个时刻通过贝叶斯更新:
p(xk∣y1:k)=p(yk∣xk)p(xk∣y1:k−1)p(yk∣y1:k−1)p(x_k|y_{1:k})=\frac{p(y_k|x_k)p(x_k|y_{1:k-1})}{p(y_k|y_{1:k-1})} p(xk∣y1:k)=p(yk∣y1:k−1)p(yk∣xk)p(xk∣y1:k−1)
由于直接求解上述贝叶斯方程通常不可行,粒子滤波器通过一组独立的粒子来近似解,粒子权重wk(i)w_k^{(i)}wk(i)反映了各粒子在时刻k−1k-1k−1的重要性。
p(xk−1∣y1:k−1)≈∑i=1Nwk−1(i)δ(xk−1−xk−1∣k−1(i))p(x_{k-1}|y_{1:k-1})\approx\sum_{i=1}^{N}w_{k-1}^{(i)}\delta(x_{k-1}-x_{k-1|k-1}^{(i)}) p(xk−1∣y1:k−1)≈i=1∑Nwk−1(i)δ(xk−1−xk−1∣k−1(i))
系统的预测步骤被近似为对粒子的加权预测:
p(xk∣y1:k−1)≈∑i=1N∫wk−1(i)δ(xk−1−xk−1∣k−1(i))p(xk∣xk−1)dxk−1=∑i=1Nwk−1(i)δ(xk−(F(xk−1∣k−1(i))+qk(i)))=∑i=1Nwk−1(i)δ(xk−xk∣k−1(i))\begin{aligned} p(x_{k}|y_{1:k-1}) & \approx\sum_{i=1}^{N}\int w_{k-1}^{(i)}\delta(x_{k-1}-x_{k-1|k-1}^{(i)})p(x_{k}|x_{k-1})dx_{k-1} \\ & =\sum_{i=1}^{N}w_{k-1}^{(i)}\delta(x_{k}-(F(x_{k-1|k-1}^{(i)})+q_{k}^{(i)})) \\ & =\sum_{i=1}^{N}w_{k-1}^{(i)}\delta(x_{k}-x_{k|k-1}^{(i)}) \end{aligned} p(xk∣y1:k−1)≈i=1∑N∫wk−1(i)δ(xk−1−xk−1∣k−1(i))p(xk∣xk−1)dxk−1=i=1∑Nwk−1(i)δ(xk−(F(xk−1∣k−1(i))+qk(i)))=i=1∑Nwk−1(i)δ(xk−xk∣k−1(i))
最终利用预测步骤和粒子权重,后验密度近似计算:
p(xk∣y1:k)≈∑i=1Nwk(i)δ(xk−xk∣k−1(i))p(x_k|y_{1:k})\approx\sum_{i=1}^Nw_k^{(i)}\delta(x_k-x_{k|k-1}^{(i)}) p(xk∣y1:k)≈i=1∑Nwk(i)δ(xk−xk∣k−1(i))
在粒子滤波中无法直接从目标分布中生成粒子,因此采用重要性采样(Importance Sampling)技术近似真实的滤波分布。粒子的权重通过与观测数据的匹配度来进行更新:
wk(i)∝wk−1(i)p(yk∣xk(i))p(xk(i)∣xk−1(i))q(xk(i)∣xk−1(i),yk)w_k^{(i)}\propto w_{k-1}^{(i)}\frac{p(y_k|x_k^{(i)})p(x_k^{(i)}|x_{k-1}^{(i)})}{q(x_k^{(i)}|x_{k-1}^{(i)},y_k)} wk(i)∝wk−1(i)q(xk(i)∣xk−1(i),yk)p(yk∣xk(i))p(xk(i)∣xk−1(i))

4.PF-JAYA算法
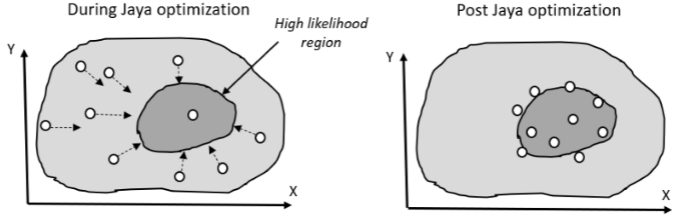
PF-JAYA算法核心思想是在粒子权重更新后,引入JAYA算法增加了粒子的多样性,并通过考虑最新观测的似然信息,帮助将粒子重新分布到高似然区域,从而不受当前粒子权重的影响。

5.结果展示
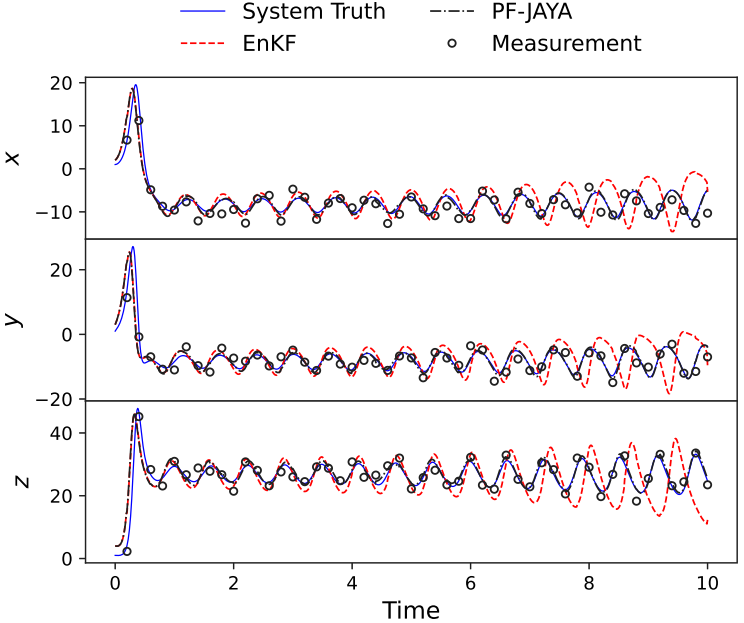
6.参考文献
[1] Amavasai A, Dijkstra J. Particle Filter based on Jaya optimisation for Bayesian updating of nonlinear models[J]. Applied Soft Computing, 2024, 158: 111429.
