Java分治算法题目练习(快速/归并排序)

颜色分类

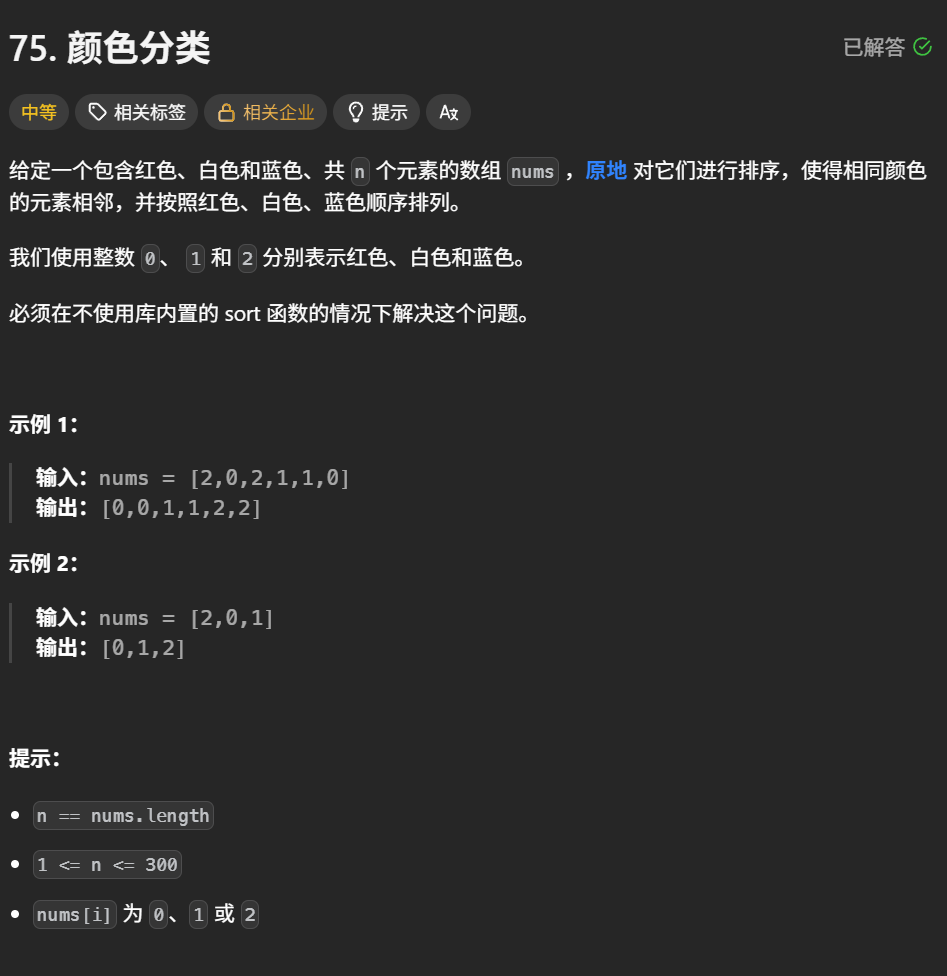
题目解析：将其数组中0放在左边，1放在中间，2放在右边
在双指针算法中有一个移动零的题目，就是将所有0元素移动到右边，但是非0元素相对位置不改变
那题使用双指针将其数组分为三部分，因此这题也可以将其数组分块
left表示为0区域最右侧，i遍历数组，right表示2区域最左侧
使用这三个指针将这个数组分为了4部分

class Solution {public void sortColors(int[] nums) {//可以将其数组分为三部分//[0,left]:全是0//[left+1,i-1]全都是1//[i,right-1]待扫描//[right,n-1]全是2int left = -1;int i = 0;int right = nums.length;while(i < right){if(nums[i] == 0){swap(nums,++left,i++);}else if(nums[i] == 1){i++;}else{swap(nums,--right,i);//此时会将right-1元素放到i下标，但是这个元素没有扫描过，所以这里不可以让i++}}}public void swap(int[] nums,int i , int j){int tem = nums[i];nums[i] = nums[j];nums[j] = tem;}
}

时间复杂度：O(n)
空间复杂度：O(1)

排序数组(快排)

题目解析：给一个数组让我们排序
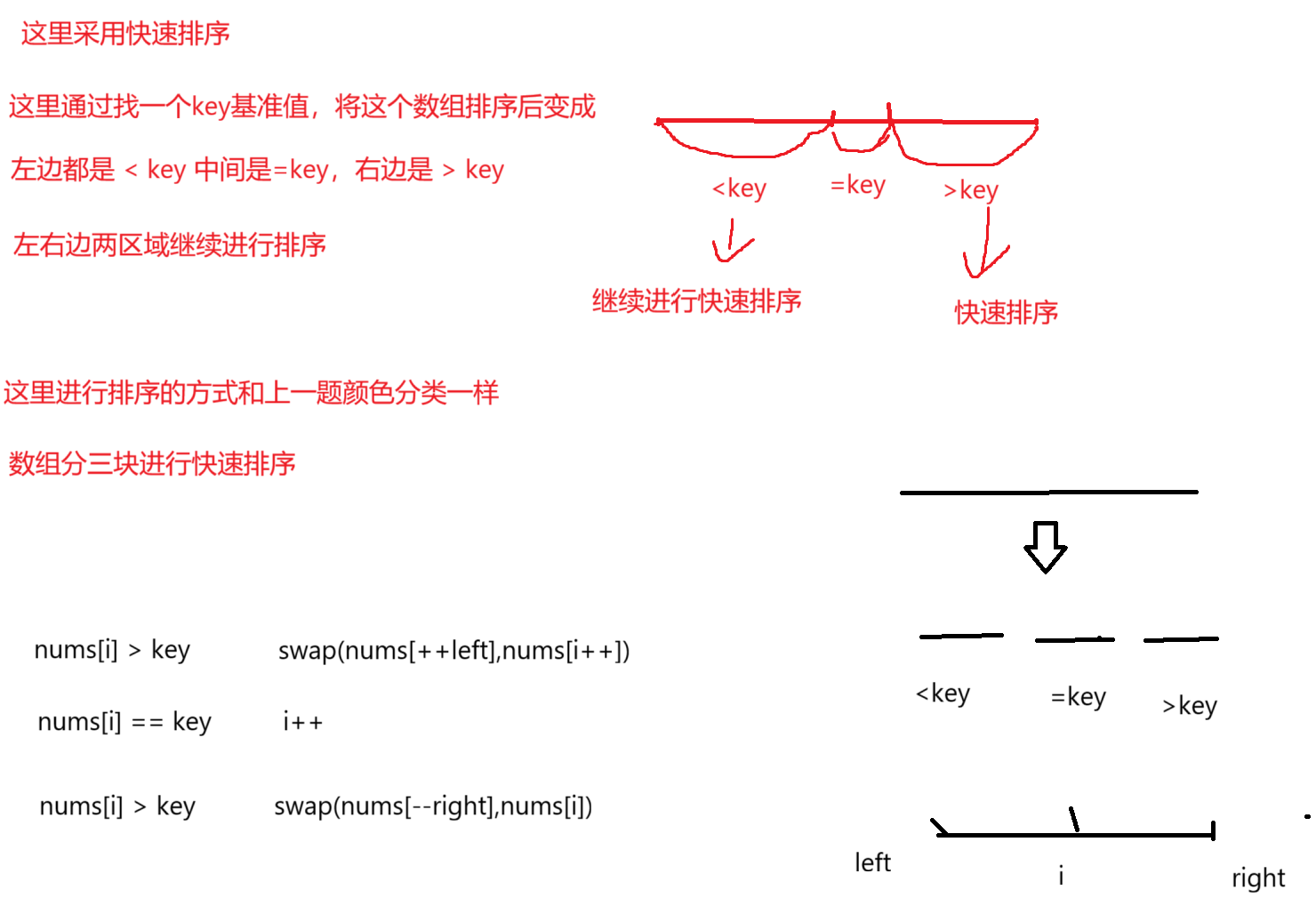
分治：使用快速排序，找一个key基准值，根据基准值，让其数组变成三个模块，左边模块<key，中间模块=key，右边模块>key，这时候在对左右两边的模块，分别进行找基准值进行排序，左右两边每一个模块又可以分为这三个部分，就这样不断排序最终结果就变成有序的了
key基准值如何取
这里采用随机取，随机其对应区间下标 r = new Random().nextInt( right - left + 1) + left，这样整个下标区间的取值就是[left,right]了

class Solution {public int[] sortArray(int[] nums) {qsort(nums,0,nums.length-1);return nums;}public void qsort(int[] nums,int l,int r){if(l >= r){return;}//这里采用随机获取key//随机的下标是[l,r];int key = nums[new Random().nextInt(r - l + 1) + l];//这里根据key将其数组分三块进行排序int left = l - 1;int right = r + 1;int i = l;while(i < right){if(nums[i] < key){swap(nums,++left,i++);}else if(nums[i] == key){i++;}else{swap(nums,--right,i);}}qsort(nums,l,left);qsort(nums,right,r);}public void swap(int[] nums,int i,int j){int tem = nums[i];nums[i] = nums[j];nums[j] = tem;}
}

数组中第K个最大元素

题目解析：给了一个数组，找出其中第K个大的元素
快速排序，根据上一题的快速排序，这里我们仍然使用快排，但是这里不一样的是，快速排序以后将数组分为三个模块，这里我们可以判断其第K个大的元素在那个模块，此时我们根据其每一个模块元素个数进行判断，在一个模块中，只需要在这一个模块中找即可，剩下的两个模块就不用管了

class Solution {public int findKthLargest(int[] nums, int k) {return qsort(nums,0,nums.length-1,k);}public int qsort(int[] nums,int l,int r,int k){if(l == r){return nums[l];}int key = nums[new Random().nextInt(r - l + 1)+l];int left = l - 1;int right = r + 1;int i = l;while(i < right){if(nums[i] < key){swap(nums,++left,i++);}else if(nums[i] == key){i++;}else{swap(nums,--right,i);}}//这里将其分为了[l,left] [left+1,right-1] [right,r]//判断其第k大的元素在那个模块int b = right - left - 1;int c = r - right + 1;if(c >= k){//只在右边找即可return  qsort(nums,right,r,k);}else if((b+c)>=k){return key;}else{return qsort(nums,l,left,k-b-c);}}public void swap(int[] nums,int i,int j){int tem = nums[i];nums[i] = nums[j];nums[j] = tem;}
}

最小的K个数

题目解析：返回数组中最小的k个数
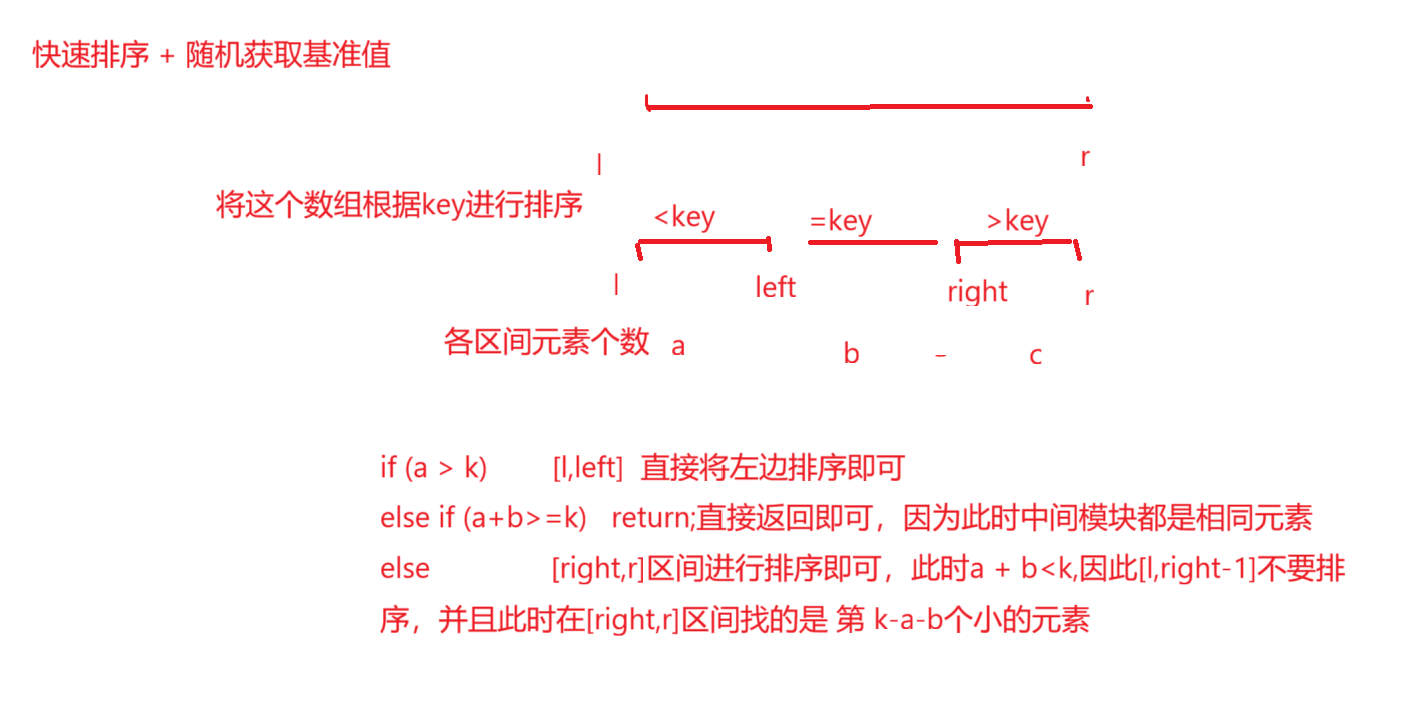
快速选择算法 + 随机获取key值
这题和上一题找出第k个最大的数类似，唯一不同的就是排序后三个模块如果处理，因为这里最小的k个数顺序是随机的，也是每次只需要调整一个模块即可，剩下的两个模块不用管了

class Solution {public int[] smallestK(int[] arr, int k) {//快速选择算法qsort(arr,0,arr.length-1,k);int[] ret = new int[k];for(int i = 0;i < k;i++){ret[i] = arr[i];}return ret;}public void qsort(int[] arr,int l ,int r ,int k){if(l >= r){return;}int key = arr[new Random().nextInt(r - l + 1) + l];int left = l - 1;int right = r + 1;int i = l;while(i < right){if(arr[i] < key){swap(arr,++left,i++);}else if(arr[i] == key){i++;}else{swap(arr,--right,i);}}//[l,left] [left + 1, right - 1],[right , r]int a = left - l + 1;int b = right - left -1;if(a > k){qsort(arr,l,left,k);}else if(a+b >= k){return;}else{qsort(arr,right,r,k-a-b);}}public void swap(int[] arr,int i,int j){int tem = arr[i];arr[i]  = arr[j];arr[j] = tem;}
}

时间复杂度：O(n)，因为随机存取key，所以渐进O(n)
空间复杂度：O(k)

排序数组(归并)

题目解析：排序
这里仍然是归并的思想，根据mid将其数组分为左右两部分，左右两部分分别进行排序，左边部分又可以分为左右两部分，右边同理，当左右两边分完以后，就可以进行合并，左边先合并，右边再合并，最后合并到一起，最终整个数组再进行一次排序即可

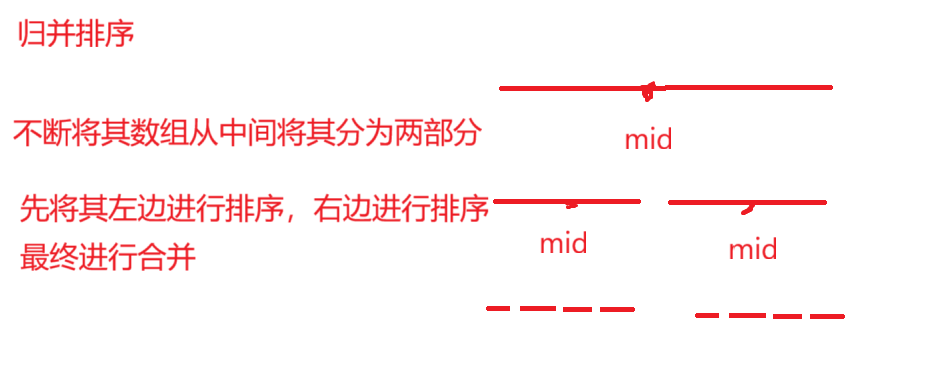
归并排序详细介绍

class Solution {int[] tem;public int[] sortArray(int[] nums) {tem = new int[nums.length];//归并排序mergeSort(nums,0,nums.length-1);return nums;}public void mergeSort(int[] nums,int left , int right){if(left >= right){return;}//根据中间点进行划分int mid = (left + right) / 2;//左右两边分别进行排序mergeSort(nums,left,mid);mergeSort(nums,mid+1,right);//int[] tem = new int[right - left + 1];//合并两个有序数组int cur1 = left;int cur2 = mid+1;int i = 0;while(cur1 <= mid && cur2 <= right){tem[i++] = nums[cur1] >= nums[cur2] ? nums[cur2++] : nums[cur1++];}//处理还没有遍历完的数组while(cur1 <= mid){tem[i++] = nums[cur1++];}while(cur2 <= right){tem[i++] = nums[cur2++];}//将排好序的数组放回去for(int j = left;j <= right;j++){nums[j] = tem[j - left];}}
}

交易逆序对的总数

题目解析：相对顺序不变，找出ai > aj , i < j，这样逆序对的总个数
算法原理：仍然采用分治的思想，采用

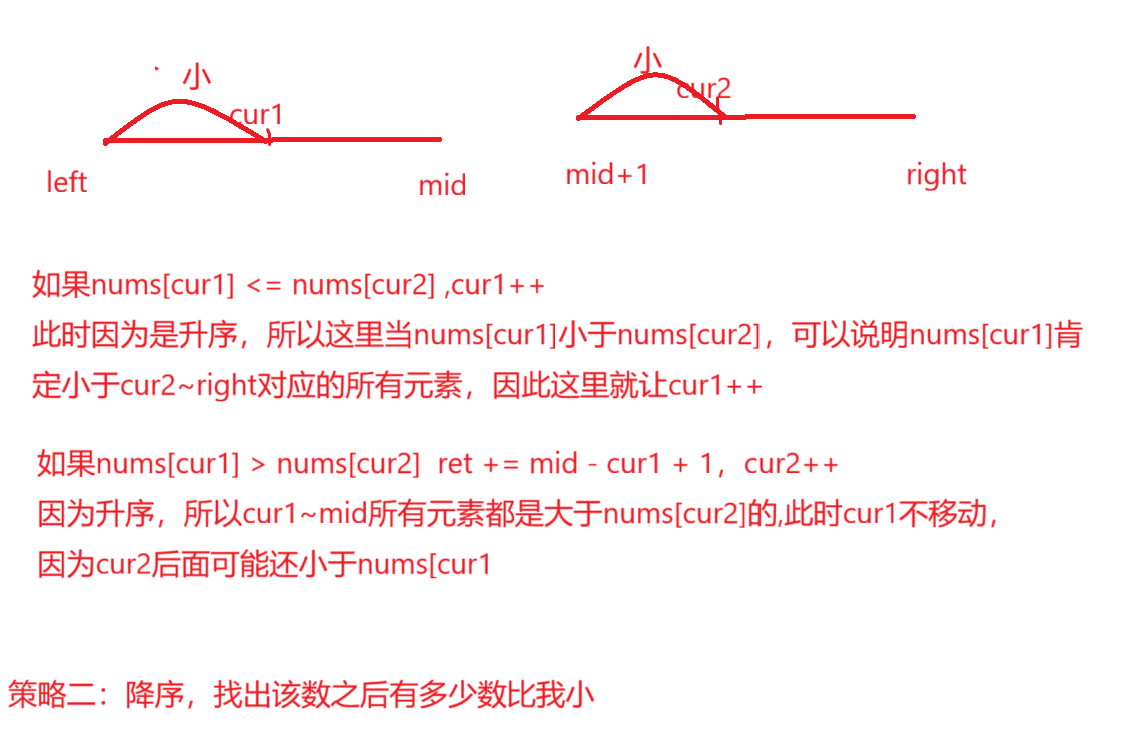
//升序
class Solution {int[] tem;public int reversePairs(int[] record) {tem = new int[record.length];//归并排序return mergeSort(record,0,record.length-1);}public int mergeSort(int[] record, int left, int right) {if (left >= right) {return 0 ;}//根据中间点进行划分int mid = (left + right) / 2;//左右两边统计分别进行排序int ret =  mergeSort(record, left, mid)+  mergeSort(record, mid + 1, right);//int[] tem = new int[right - left + 1];//一左一右的个数+排序//合并两个有序数组int cur1 = left;int cur2 = mid + 1;int i = 0;while (cur1 <= mid && cur2 <= right) {if (record[cur1] <= record[cur2]) {//cur1向后走，此时没有tem[i++] = record[cur1++];} else {ret += mid - cur1 + 1;tem[i++] = record[cur2++];}}//处理还没有遍历完的数组while (cur1 <= mid) {tem[i++] = record[cur1++];}while (cur2 <= right) {tem[i++] = record[cur2++];}//将排好序的数组放回去for (int j = left; j <= right; j++) {record[j] = tem[j - left];}return ret;}}

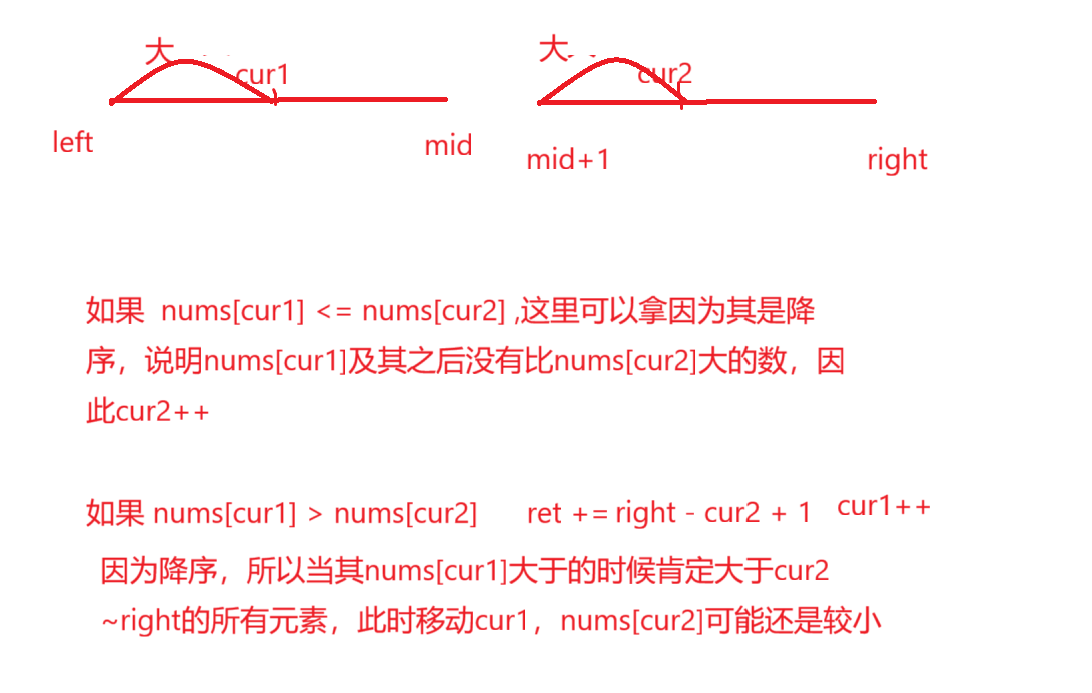
//降序
class Solution {//降序就是找后面又几个数比我小int[] tem;public int reversePairs(int[] record) {tem = new int[record.length];//归并排序return mergeSort(record,0,record.length-1);}public int mergeSort(int[] record, int left, int right) {if (left >= right) {return 0 ;}//根据中间点进行划分int mid = (left + right) / 2;//左右两边统计分别进行排序int ret =  mergeSort(record, left, mid)+  mergeSort(record, mid + 1, right);//int[] tem = new int[right - left + 1];//一左一右的个数+排序//合并两个有序数组int cur1 = left;int cur2 = mid + 1;int i = 0;while (cur1 <= mid && cur2 <= right) {if (record[cur1] <= record[cur2]) {//cur1向后走，此时没有tem[i++] = record[cur2++];} else {ret += right - cur2 + 1;tem[i++] = record[cur1++];}}//处理还没有遍历完的数组while (cur1 <= mid) {tem[i++] = record[cur1++];}while (cur2 <= right) {tem[i++] = record[cur2++];}//将排好序的数组放回去for (int j = left; j <= right; j++) {record[j] = tem[j - left];}return ret;}}

翻转对

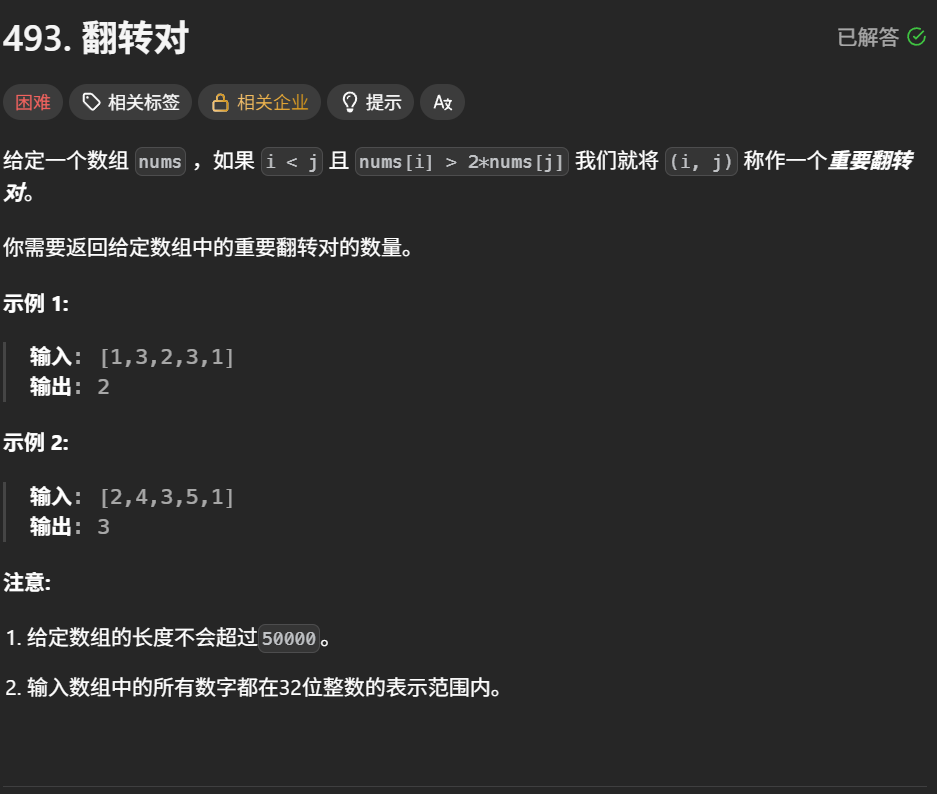
题目解析：找出前面一个元素大于后面元素2倍的总个数
归并：此题目和上题一样，只不过这里变成了2倍，上面我们将更新结果和合并数组放到一起，这里我们因为条件不同，所以要将其分分开写即可

这里2倍可能会溢出，因此直接让前一个数 / 2.0进行比较即可

//降序
class Solution {int[] tem;public int reversePairs(int[] nums) {int n = nums.length;tem = new int[n];return mergeSort(nums,0,n-1);}public int mergeSort(int[] nums,int left,int right){if(left >= right){return 0;}int ret = 0;int mid = (left + right) / 2;ret += mergeSort(nums,left,mid);ret += mergeSort(nums,mid+1,right);//先计算翻转对的个数int cur1 = left;int cur2 = mid+1;//降序while(cur1 <= mid){while(cur2 <= right && nums[cur1]/2.0 <= nums[cur2]){cur2++;}if(cur2 > right){break;}//更新结果ret += right - cur2 + 1;cur1++;}//合并两个有序数组cur1 = left;cur2 = mid+1;int i = left;while(cur1 <= mid && cur2<=right){tem[i++] = nums[cur1] >= nums[cur2] ? nums[cur1++] : nums[cur2++];}//处理剩余while(cur1 <= mid){tem[i++] = nums[cur1++];}while(cur2 <= right){tem[i++] = nums[cur2++];}for(int j = left;j <= right;j++){nums[j] = tem[j];}return ret;}
}

//升序
class Solution {int[] tem;public int reversePairs(int[] nums) {int n = nums.length;tem = new int[n];return mergeSort(nums,0,n-1);}public int mergeSort(int[] nums,int left,int right){if(left >= right){return 0;}int ret = 0;int mid = (left + right) / 2;ret += mergeSort(nums,left,mid);ret += mergeSort(nums,mid+1,right);//先计算翻转对的个数int cur1 = left;int cur2 = mid+1;//降序while(cur2 <= right){while(cur1 <= mid && nums[cur1]/2.0 <= nums[cur2]){cur1++;}if(cur1 > mid){break;}//更新结果ret += mid - cur1 + 1;cur2++;}//合并两个有序数组cur1 = left;cur2 = mid+1;int i = left;while(cur1 <= mid && cur2<=right){tem[i++] = nums[cur1] >= nums[cur2] ? nums[cur2++] : nums[cur1++];}//处理剩余while(cur1 <= mid){tem[i++] = nums[cur1++];}while(cur2 <= right){tem[i++] = nums[cur2++];}for(int j = left;j <= right;j++){nums[j] = tem[j];}return ret;}
}

计算右侧小于当前元素的个数

题目解析：返回一个新数组，对应下标的值是后面元素比当前下标元素小的个数
归并：这一题和上面一题非常类似，但是唯一问题，就是我们不断排序，不断更新结果，然而我们找不到其原本下标进行更新结果，因此这里我们就需要使用一个index数组进行存放原本下标，因此也需要一个临时数组存放临时下标

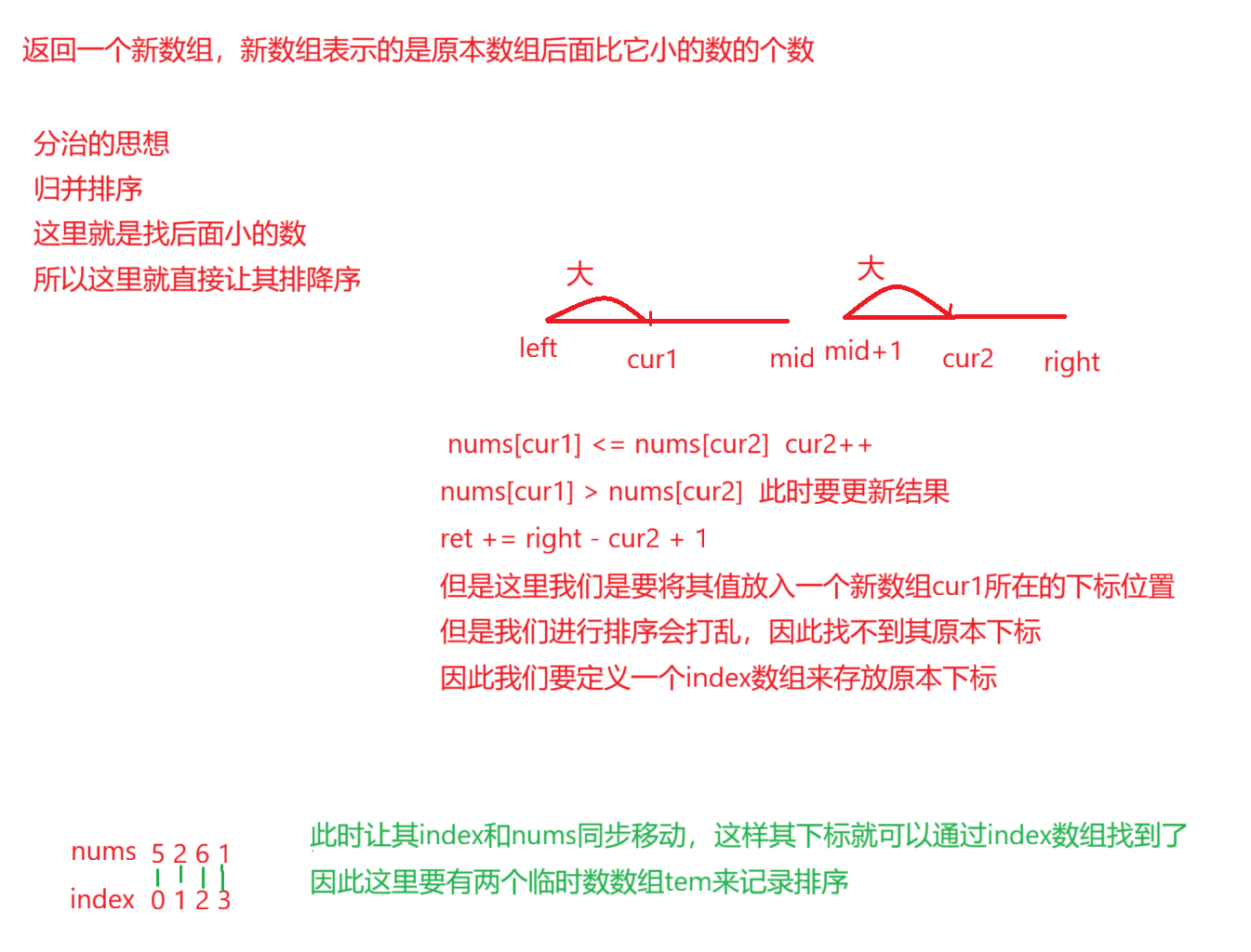
class Solution {int[] ret;//返回结果int[] index;//对应下标int[] temIndex;int[] temNums;public List<Integer> countSmaller(int[] nums) {int n = nums.length;ret = new int[n];index = new int[n];temIndex = new int[n];temNums = new int[n];//初始化对应下标for (int i = 0; i < n; i++) {index[i] = i;}mergeSort(nums, 0, n - 1);List<Integer> l = new ArrayList<>();for(int x : ret){l.add(x);}return l;}public void mergeSort(int[] nums, int left, int right) {if (left >= right) {return;}int mid = (left + right) / 2;mergeSort(nums, left, mid);mergeSort(nums, mid + 1, right);int cur1 = left;int cur2 = mid + 1;int i = 0;//进行排序while (cur1 <= mid && cur2 <= right) {//降序if (nums[cur1] <= nums[cur2]) {temNums[i] = nums[cur2];//这里要注意对应下标移动temIndex[i++] = index[cur2++];} else {//更新结果,此时找到cur1对应的下标进行赋值ret[index[cur1]] += right - cur2 + 1;temNums[i] = nums[cur1];temIndex[i++] = index[cur1++];//更新下标}}//剩余进行排序while (cur1 <= mid) {temNums[i] = nums[cur1];temIndex[i++] = index[cur1++];}while (cur2 <= right) {temNums[i] = nums[cur2];temIndex[i++] = index[cur2++];}//合并for (int j = left; j <= right; j++) {nums[j] = temNums[j - left];//下标也要更新index[j] = temIndex[j - left];}}
}