当前位置：首页 > news >正文

我爱学算法之—— 字符串

news 2025/11/17 7:19:15

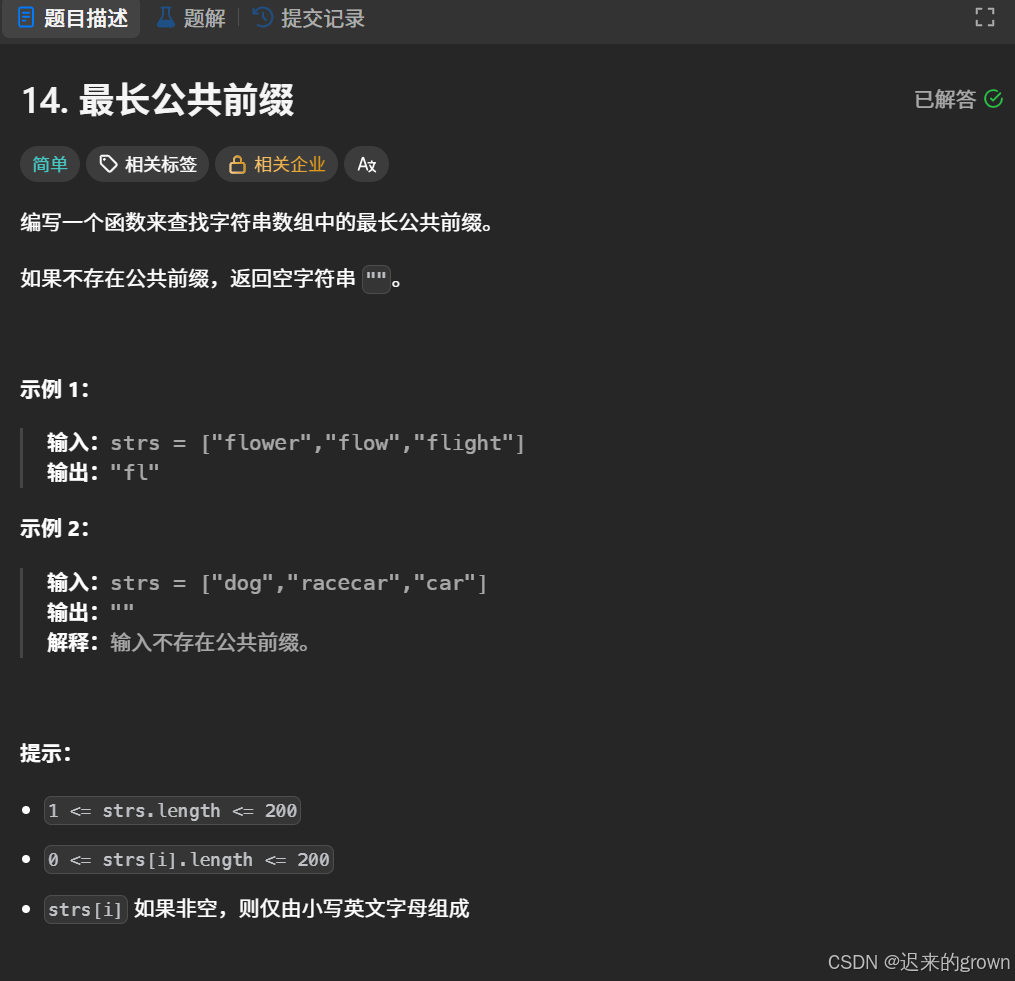
一、最长公共前缀

题目解析

在这里插入图片描述

算法思路

这里就可以直接拿第一个字符串当 “参照”，逐位检查所有字符串是不是都有相同的字符：

先以第一个字符串的长度为限，逐个看它的每个字符（从第 0 位开始）
对每一位（比如第 i 位），先记下第一个字符串在这一位的字符 ch
然后去检查其他所有字符串：
- 如果有哪个字符串的第 i 位和 ch不一样，说明公共前缀到第 i 位之前就结束了，直接返回第一个字符串从 0 到 i - 位的子串
- 如果所有字符串的第 i 位都和 ch 一样，就继续检查下一位
要是把第一个字符串的所有位都检查完了，所有字符串对应位置都相同，那整个第一个字符串就是最长公共前缀，直接返回它

这样一步步比对，直到找到不匹配的位置，就能快速确定最长的公共前缀了。

代码实现

class Solution {
public:string longestCommonPrefix(vector<string>& strs) {int n = strs[0].size();for (int i = 0; i < n; i++) {char ch = strs[0][i];for (int j = 1; j < strs.size(); j++) {if (strs[j][i] != ch)return strs[0].substr(0, i);}}return strs[0];}
};

二、最长回文子串

题目解析

在这里插入图片描述

算法思路

该算法采用中心扩展法求解最长回文子串，具体思路如下：

考虑回文子串的两种中心形式：
- 奇数长度的回文子串，中心为单个字符（如 “aba” 的中心是 ‘b’）。
- 偶数长度的回文子串，中心为两个相邻字符之间的位置（如 “abba” 的中心在两个 ‘b’ 之间）。
遍历每个可能的中心并扩展：
- 对字符串中的每个位置k，分别以两种中心形式进行扩展：
  - 以k为中心（奇数长度）：初始化左指针i = k - 1，右指针j = k + 1，在i和j的合法范围内（不越界），若i和j位置的字符相等，则继续向左、右移动指针扩展。
  - 以k和k+1之间为中心（偶数长度）：初始化左指针i = k，右指针j = k + 1，同样在合法范围内比对i和j位置的字符，相等则继续扩展。
记录最长回文子串的信息：
- 每次扩展结束后，计算当前回文子串的长度（j - i - 1）。
- 若该长度大于已记录的最大长度，则更新最大长度和对应的起始位置（i + 1）。
生成结果：
- 遍历结束后，根据记录的最长回文子串的起始位置和长度，从原字符串中截取并返回该子串。

通过遍历所有可能的中心并扩展检查，该算法可找出字符串中最长的回文子串。

代码实现

class Solution {
public:string longestPalindrome(string s) {int len = 0;int max_i = 0;int n = s.size();for (int k = 0; k < n; k++) {int i = k, j = k + 1;while (i >= 0 && j < n && s[i] == s[j]) {i--;j++;}if (j - i - 1 > len) {len = j - i - 1;max_i = i + 1;}i = k - 1;j = k + 1;while (i >= 0 && j < n && s[i] == s[j]) {i--;j++;}if (j - i - 1 > len) {len = j - i - 1;max_i = i + 1;}}return s.substr(max_i, len);}
};

三、二进制求和

题目解析

在这里插入图片描述

算法思路

整体来说，高精度计算就是模拟加法的整个过程，做好进位处理等细节问题即可。

从两个二进制字符串a和b的末尾（最低位）开始，用指针i和j遍历，同时维护进位tmp。
逐位计算对应位置的和（含进位），取当前位结果（和对 2 取余）存入结果字符串，更新进位（和除以 2）。
处理其中一个字符串剩余的高位，与进位继续计算。
若最终仍有进位，将其加入结果。
反转结果字符串（因计算时从低位到高位存储），得到最终和

代码实现

class Solution {
public:string addBinary(string a, string b) {string ret;int i = a.size() - 1, j = b.size() - 1;int tmp = 0;while (i >= 0 && j >= 0) {// 倒序计算int x = (a[i] - '0') + (b[j] - '0') + tmp;tmp = x / 2;x %= 2;ret.push_back(x + '0');i--;j--;}while (i >= 0) {int x = (a[i] - '0') + tmp;tmp = x / 2;x %= 2;ret.push_back(x + '0');i--;}while (j >= 0) {int x = (b[j] - '0') + tmp;tmp = x / 2;x %= 2;ret.push_back(x + '0');j--;}if (tmp != 0)ret.push_back(tmp + '0');reverse(ret.begin(), ret.end());return ret;}
};

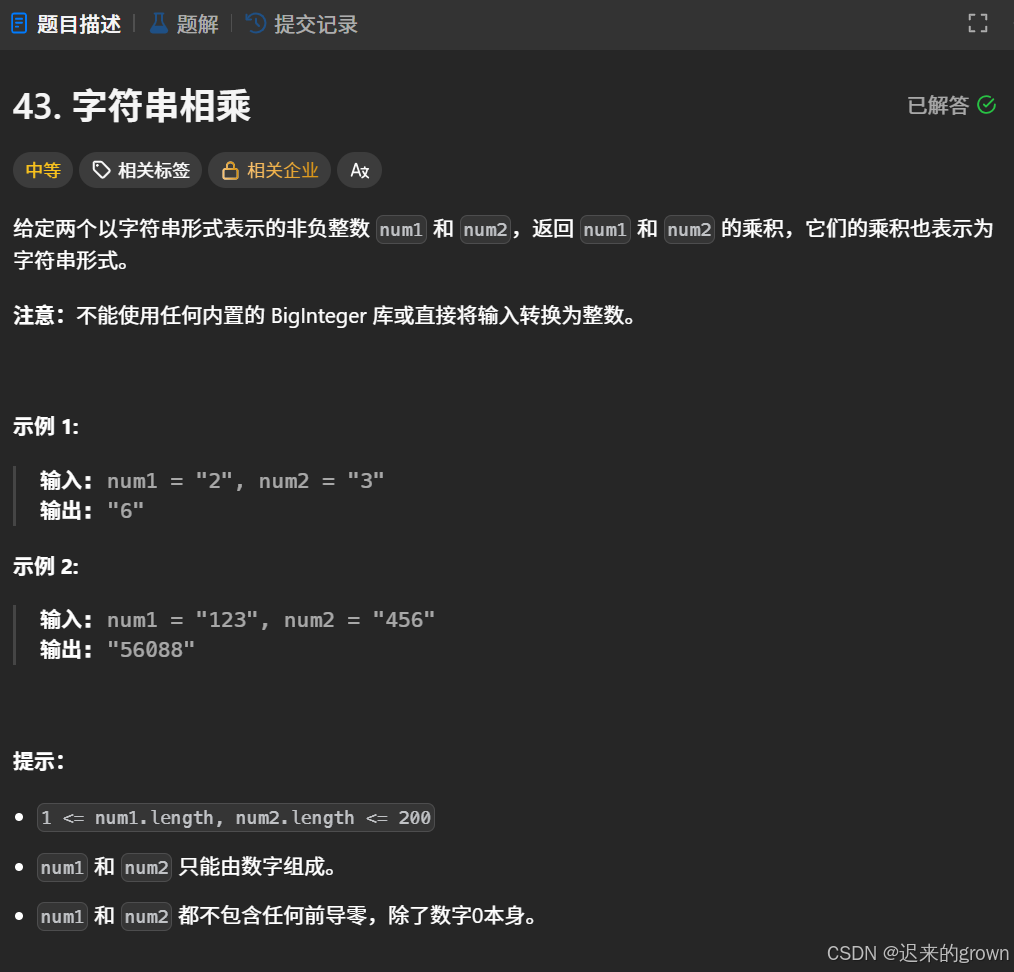
四、字符串相乘

题目解析

在这里插入图片描述

算法思路

初始化存储结果的数组：创建长度为两字符串长度之和的数组vt，用于暂存每一步的乘积。
逐位相乘并累加：

从两个字符串的低位（末尾）开始，将num1的第i位与num2的第j位相乘，结果累加到vt[i+j]中。
处理进位：遍历vt，将每一位的值加上进位后，更新当前位为对 10 取余的结果，进位为除以 10 的商。若最后仍有进位，追加到数组末尾。
转换为字符串：跳过数组末尾的无效 0，从有效最高位开始，将数组元素转换为字符并拼接，若结果为空则返回 “0”。

通过分步处理乘法和进位，实现大整数字符串的相乘。

代码实现

class Solution {
public:string multiply(string num1, string num2) {int n = num1.size(), m = num2.size();vector<int> vt(n + m, 0);// 先乘for (int i = 0; i < n; i++) {//for (int j = 0; j < m; j++) {int x = (num1[n - 1 - i] - '0') * (num2[m - 1 - j] - '0');vt[i + j] += x;}}// 处理进位int tmp = 0;for (int i = 0; i < n + m; i++) {int x = vt[i] + tmp;tmp = x / 10;vt[i] = x % 10;}if (tmp != 0)vt.push_back(tmp);// 转换成字符串string ret;int i = n + m - 1;while (i >= 0 && vt[i] == 0)i--;while (i >= 0) {ret.push_back(vt[i] + '0');i--;}if (ret.empty())ret.push_back('0');return ret;}
};