插值——Hermite 插值与分段三次 Hermite 插值
插值——Hermite 插值与分段三次 Hermite 插值
- 一、Hermite 插值
- 1. 插值目标
- 2. Hermite 插值多项式的构造(基函数法)
- 3. 插值余项(误差公式)
- 二、分段三次 Hermite 插值(PCHIP)
- 1. 动机
- 2. 插值设定
- 3. 分段三次 Hermite 多项式的显式表达
- 4. 导数估计(当 mim_imi 未知时)
- (1) 三点差商(简单估计):
- (2) Fritsch–Carlson 方法(保形 PCHIP):
- 5. 全局性质
- 三、Python 实现
- 四、结果
- 附:文章说明
Hermite 插值(Hermite Interpolation) 是一种在给定节点处不仅匹配函数值,还匹配一阶(或高阶)导数值的多项式插值方法。
一、Hermite 插值
1. 插值目标
设在区间 [a,b][a, b][a,b] 上给定 n+1n+1n+1 个互异节点:
x0,x1,…,xnx_0, x_1, \dots, x_n x0,x1,…,xn
并已知函数值 yi=f(xi)y_i = f(x_i)yi=f(xi) 和一阶导数值 mi=f′(xi)m_i = f'(x_i)mi=f′(xi),i=0,1,…,ni = 0, 1, \dots, ni=0,1,…,n。
目标:构造一个次数不超过 2n+12n+12n+1 的多项式 H2n+1(x)H_{2n+1}(x)H2n+1(x),满足:
{H2n+1(xi)=yiH2n+1′(xi)=mifor i=0,1,…,n\begin{cases} H_{2n+1}(x_i) = y_i \\ H_{2n+1}'(x_i) = m_i \end{cases} \quad \text{for } i = 0, 1, \dots, n {H2n+1(xi)=yiH2n+1′(xi)=mifor i=0,1,…,n
这样的插值条件共有 2(n+1)2(n+1)2(n+1) 个,因此存在唯一的次数 ≤2n+1\le 2n+1≤2n+1 的多项式满足上述条件。
2. Hermite 插值多项式的构造(基函数法)
定义两组 Hermite 基函数 {hi(x)}\{h_i(x)\}{hi(x)} 和 {h^i(x)}\{\hat{h}_i(x)\}{h^i(x)},满足:
- hi(xj)=δij,hi′(xj)=0h_i(x_j) = \delta_{ij}, \quad h_i'(x_j) = 0hi(xj)=δij,hi′(xj)=0
- h^i(xj)=0,h^i′(xj)=δij\hat{h}_i(x_j) = 0, \quad \hat{h}_i'(x_j) = \delta_{ij}h^i(xj)=0,h^i′(xj)=δij
则 Hermite 插值多项式为:
H2n+1(x)=∑i=0nyihi(x)+∑i=0nmih^i(x)H_{2n+1}(x) = \sum_{i=0}^{n} y_i \, h_i(x) + \sum_{i=0}^{n} m_i \, \hat{h}_i(x) H2n+1(x)=i=0∑nyihi(x)+i=0∑nmih^i(x)
其中基函数可由 Lagrange 基函数 Li(x)L_i(x)Li(x) 构造:
- Li(x)=∏j=0j≠inx−xjxi−xjL_i(x) = \prod_{\substack{j=0 \\ j \ne i}}^{n} \frac{x - x_j}{x_i - x_j}Li(x)=∏j=0j=inxi−xjx−xj
- 令 Ai(x)=[1−2(x−xi)Li′(xi)]Li2(x)A_i(x) = \left[1 - 2(x - x_i)L_i'(x_i)\right] L_i^2(x)Ai(x)=[1−2(x−xi)Li′(xi)]Li2(x)
- 令 Bi(x)=(x−xi)Li2(x)B_i(x) = (x - x_i) L_i^2(x)Bi(x)=(x−xi)Li2(x)
则:
hi(x)=Ai(x),h^i(x)=Bi(x)h_i(x) = A_i(x), \quad \hat{h}_i(x) = B_i(x) hi(x)=Ai(x),h^i(x)=Bi(x)
于是:
H2n+1(x)=∑i=0n[yiAi(x)+miBi(x)]H_{2n+1}(x) = \sum_{i=0}^{n} \left[ y_i A_i(x) + m_i B_i(x) \right] H2n+1(x)=i=0∑n[yiAi(x)+miBi(x)]
3. 插值余项(误差公式)
若 f∈C2n+2[a,b]f \in C^{2n+2}[a, b]f∈C2n+2[a,b],则对任意 x∈[a,b]x \in [a, b]x∈[a,b],存在 ξ∈(a,b)\xi \in (a, b)ξ∈(a,b) 使得:
f(x)−H2n+1(x)=f(2n+2)(ξ)(2n+2)!∏i=0n(x−xi)2f(x) - H_{2n+1}(x) = \frac{f^{(2n+2)}(\xi)}{(2n+2)!} \prod_{i=0}^{n} (x - x_i)^2 f(x)−H2n+1(x)=(2n+2)!f(2n+2)(ξ)i=0∏n(x−xi)2
注意:误差项中每个节点出现两次,这便体现出导数匹配带来的更高阶插值接触。
二、分段三次 Hermite 插值(PCHIP)
1. 动机
全局 Hermite 插值使用高次多项式,易产生 Runge 振荡,且对导数误差敏感。
分段三次 Hermite 插值将区间划分为子区间,在每个子区间上构造一个三次多项式,仅依赖该区间端点的函数值与导数值。
2. 插值设定
给定节点:
x0<x1<⋯<xn,yi=f(xi),mi=f′(xi)(或估计值)x_0 < x_1 < \cdots < x_n, \quad y_i = f(x_i), \quad m_i = f'(x_i) \ (\text{或估计值}) x0<x1<⋯<xn,yi=f(xi),mi=f′(xi) (或估计值)
在每个子区间 [xi,xi+1][x_i, x_{i+1}][xi,xi+1] 上构造三次多项式 Hi(x)H_i(x)Hi(x),满足:
{Hi(xi)=yiHi(xi+1)=yi+1Hi′(xi)=miHi′(xi+1)=mi+1\begin{cases} H_i(x_i) = y_i \\ H_i(x_{i+1}) = y_{i+1} \\ H_i'(x_i) = m_i \\ H_i'(x_{i+1}) = m_{i+1} \end{cases} ⎩⎨⎧Hi(xi)=yiHi(xi+1)=yi+1Hi′(xi)=miHi′(xi+1)=mi+1
3. 分段三次 Hermite 多项式的显式表达
令区间长度 hi=xi+1−xih_i = x_{i+1} - x_ihi=xi+1−xi,并令归一化参数:
t=x−xihi∈[0,1]t = \frac{x - x_i}{h_i} \in [0, 1] t=hix−xi∈[0,1]
则:
Hi(x)=yih00(t)+yi+1h10(t)+himih01(t)+himi+1h11(t)H_i(x) = y_i \, h_{00}(t) + y_{i+1} \, h_{10}(t) + h_i m_i \, h_{01}(t) + h_i m_{i+1} \, h_{11}(t) Hi(x)=yih00(t)+yi+1h10(t)+himih01(t)+himi+1h11(t)
其中 Hermite 基函数为:
h00(t)=2t3−3t2+1h10(t)=−2t3+3t2h01(t)=t3−2t2+th11(t)=t3−t2\begin{aligned} h_{00}(t) &= 2t^3 - 3t^2 + 1 \\ h_{10}(t) &= -2t^3 + 3t^2 \\ h_{01}(t) &= t^3 - 2t^2 + t \\ h_{11}(t) &= t^3 - t^2 \end{aligned} h00(t)h10(t)h01(t)h11(t)=2t3−3t2+1=−2t3+3t2=t3−2t2+t=t3−t2
这些基函数满足:
- h00(0)=1,h00(1)=0,h00′(0)=h00′(1)=0h_{00}(0)=1, h_{00}(1)=0, h_{00}'(0)=h_{00}'(1)=0h00(0)=1,h00(1)=0,h00′(0)=h00′(1)=0
- h10(0)=0,h10(1)=1,h10′(0)=h10′(1)=0h_{10}(0)=0, h_{10}(1)=1, h_{10}'(0)=h_{10}'(1)=0h10(0)=0,h10(1)=1,h10′(0)=h10′(1)=0
- h01(0)=0,h01(1)=0,h01′(0)=1,h01′(1)=0h_{01}(0)=0, h_{01}(1)=0, h_{01}'(0)=1, h_{01}'(1)=0h01(0)=0,h01(1)=0,h01′(0)=1,h01′(1)=0
- h11(0)=0,h11(1)=0,h11′(0)=0,h11′(1)=1h_{11}(0)=0, h_{11}(1)=0, h_{11}'(0)=0, h_{11}'(1)=1h11(0)=0,h11(1)=0,h11′(0)=0,h11′(1)=1
因此,Hi(x)H_i(x)Hi(x) 精确匹配端点函数值与导数值。
4. 导数估计(当 mim_imi 未知时)
若仅给定 yiy_iyi,需估计 mim_imi。常用方法包括:
(1) 三点差商(简单估计):
mi={y1−y0x1−x0,i=0yi+1−yi−1xi+1−xi−1,1≤i≤n−1yn−yn−1xn−xn−1,i=nm_i = \begin{cases} \displaystyle \frac{y_1 - y_0}{x_1 - x_0}, & i = 0 \\ \displaystyle \frac{y_{i+1} - y_{i-1}}{x_{i+1} - x_{i-1}}, & 1 \le i \le n-1 \\ \displaystyle \frac{y_n - y_{n-1}}{x_n - x_{n-1}}, & i = n \end{cases} mi=⎩⎨⎧x1−x0y1−y0,xi+1−xi−1yi+1−yi−1,xn−xn−1yn−yn−1,i=01≤i≤n−1i=n
(2) Fritsch–Carlson 方法(保形 PCHIP):
- 计算相邻区间长度:hi=xi+1−xih_i = x_{i+1} - x_ihi=xi+1−xi
- 计算割线斜率:di=yi+1−yihid_i = \dfrac{y_{i+1} - y_i}{h_i}di=hiyi+1−yi
- 对内部节点 i=1,2,…,n−1i = 1, 2, \dots, n-1i=1,2,…,n−1:
- 若 di−1di>0d_{i-1} d_i > 0di−1di>0(即单调区间),则设:
mi=3(hi−1+hi)2hidi−1+hi−1dim_i = \frac{3(h_{i-1} + h_i)}{ \displaystyle \frac{2h_i}{d_{i-1}} + \frac{h_{i-1}}{d_i} } mi=di−12hi+dihi−13(hi−1+hi)
(这是 di−1d_{i-1}di−1 和 did_idi 的加权调和平均,权重与区间长度相关); - 若 di−1di≤0d_{i-1} d_i \le 0di−1di≤0(即极值点附近),则设 mi=0m_i = 0mi=0。
- 若 di−1di>0d_{i-1} d_i > 0di−1di>0(即单调区间),则设:
该公式保证插值函数在数据单调区间内严格单调,且导数连续。
5. 全局性质
- 连续性:H(x)H(x)H(x) 在 [x0,xn][x_0, x_n][x0,xn] 上连续(C0C^0C0);
- 一阶导数连续:H′(xi−)=H′(xi+)=miH'(x_i^-) = H'(x_i^+) = m_iH′(xi−)=H′(xi+)=mi,故为 C1C^1C1;
- 非全局光滑:二阶导数一般不连续;
- 局部性:修改一个节点仅影响相邻两段;
- 保形性:若使用 PCHIP 导数估计,则能保持单调性、凸性等几何特征。
三、Python 实现
import os
import numpy as np
import matplotlib.pyplot as plt
import matplotlibmatplotlib.rcParams['font.sans-serif'] = ['SimHei']
matplotlib.rcParams['axes.unicode_minus'] = False# ========== 配置参数 ==========
INTERVAL = (-5.0, 5.0)
N = 10 # 节点数 = N + 1
RESULT_DIR = 输出目录# ========== 目标函数 ==========
def f(x):return np.sin(x) + np.cos(2 * x)def f_prime(x):return np.cos(x) - 2 * np.sin(2 * x)# ========== PCHIP 导数估计(标准 Fritsch–Carlson 方法) ==========
def estimate_derivatives(x, y):"""使用标准 Fritsch-Carlson 方法估计 PCHIP 的节点导数。Parameters:x : array-like, 节点坐标 (长度 n)y : array-like, 节点函数值 (长度 n)Returns:m : ndarray, 估计的导数值 (长度 n)"""n = len(x)if n < 2:return np.zeros(n)# 计算区间长度 h[i] = x[i+1] - x[i]h = np.diff(x)# 计算割线斜率 d[i] = (y[i+1] - y[i]) / h[i]d = np.diff(y) / hm = np.zeros(n)# 处理内部节点 i = 1, ..., n-2for i in range(1, n - 1):if d[i - 1] * d[i] > 0: # 同号,处于单调区间numerator = 3 * (h[i - 1] + h[i])denominator = (2 * h[i]) / d[i - 1] + (h[i - 1]) / d[i]m[i] = numerator / denominatorelse: # 异号或为零,设为极值点m[i] = 0.0# 边界点处理:使用单侧差商m[0] = d[0]m[-1] = d[-1]return m# ========== 分段三次 Hermite 求值 ==========
def pchip_interp(x_nodes, y_nodes, m_nodes, x_query):x_query = np.asarray(x_query)y_interp = np.empty_like(x_query, dtype=float)for idx, x in enumerate(x_query):# 找到 x 所在区间if x <= x_nodes[0]:i = 0elif x >= x_nodes[-1]:i = len(x_nodes) - 2else:i = np.searchsorted(x_nodes, x) - 1i = np.clip(i, 0, len(x_nodes) - 2)h = x_nodes[i + 1] - x_nodes[i]t = (x - x_nodes[i]) / hh00 = 2 * t**3 - 3 * t**2 + 1h10 = -2 * t**3 + 3 * t**2h01 = t**3 - 2 * t**2 + th11 = t**3 - t**2y_interp[idx] = (y_nodes[i] * h00 +y_nodes[i + 1] * h10 +h * m_nodes[i] * h01 +h * m_nodes[i + 1] * h11)return y_interp# ========== 主程序 ==========
def main():os.makedirs(RESULT_DIR, exist_ok=True)a, b = INTERVALx_nodes = np.linspace(a, b, N + 1)y_nodes = f(x_nodes)m_true = f_prime(x_nodes)m_est = estimate_derivatives(x_nodes, y_nodes)x_test = np.linspace(a, b, 1000)y_true = f(x_test)y_hermite_true = pchip_interp(x_nodes, y_nodes, m_true, x_test)y_hermite_est = pchip_interp(x_nodes, y_nodes, m_est, x_test)mae_true = np.mean(np.abs(y_hermite_true - y_true))mae_est = np.mean(np.abs(y_hermite_est - y_true))print(f"使用真实导数的 MAE: {mae_true:.6f}")print(f"使用估计导数的 MAE: {mae_est:.6f}")plt.figure(figsize=(12, 6))plt.plot(x_test, y_true, 'k-', label=r'真实函数 $f(x) = \sin x + \cos(2x)$')plt.plot(x_test, y_hermite_true, 'b--', label='Hermite(真实导数)')plt.plot(x_test, y_hermite_est, 'g-.', label='PCHIP(估计导数)')plt.scatter(x_nodes, y_nodes, color='red', zorder=5, label='插值节点')plt.grid(True, linestyle=':', alpha=0.7)plt.legend()plt.title(f'分段三次 Hermite 插值(节点数: {N + 1})')plt.xlabel('x')plt.ylabel('y')plt.tight_layout()plot_path = os.path.join(RESULT_DIR, 'hermite_pchip.png')plt.savefig(plot_path, dpi=300)print(f"结果图已保存至: {plot_path}")plt.show()if __name__ == '__main__':main()
四、结果
使用真实导数的 MAE: 0.001251
使用估计导数的 MAE: 0.055264
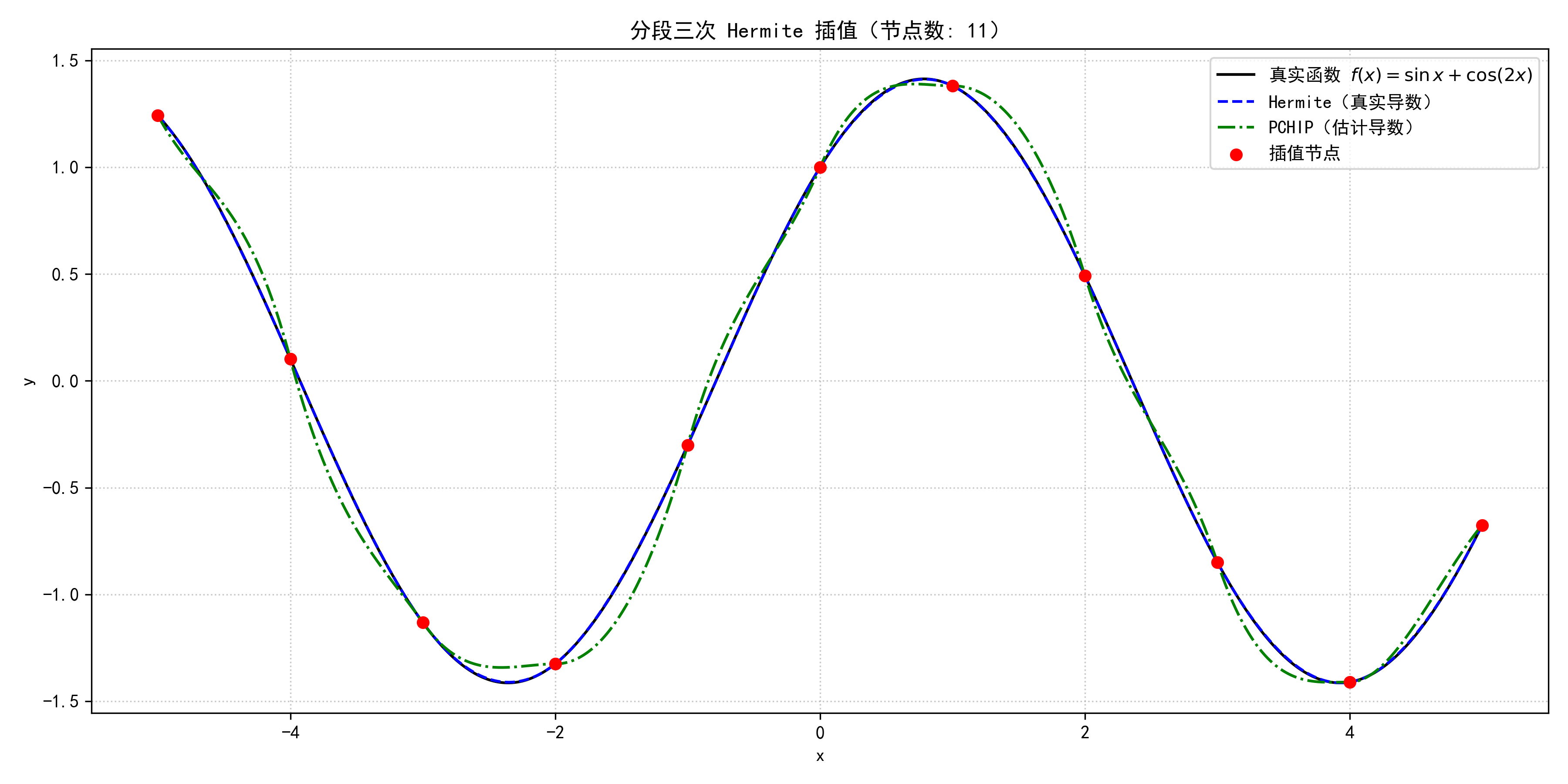
- 使用真实导数的 Hermite 插值精度极高;
- 使用 PCHIP 估计导数 仍能保持良好逼近;
当真实函数为
f(x)=sinx+cos2x,x∈[a,b]f(x) = \sin x + \cos 2x, \quad x \in [a, b] f(x)=sinx+cos2x,x∈[a,b]
时,输出为:
使用真实导数的 MAE: 0.014374
使用估计导数的 MAE: 0.156054
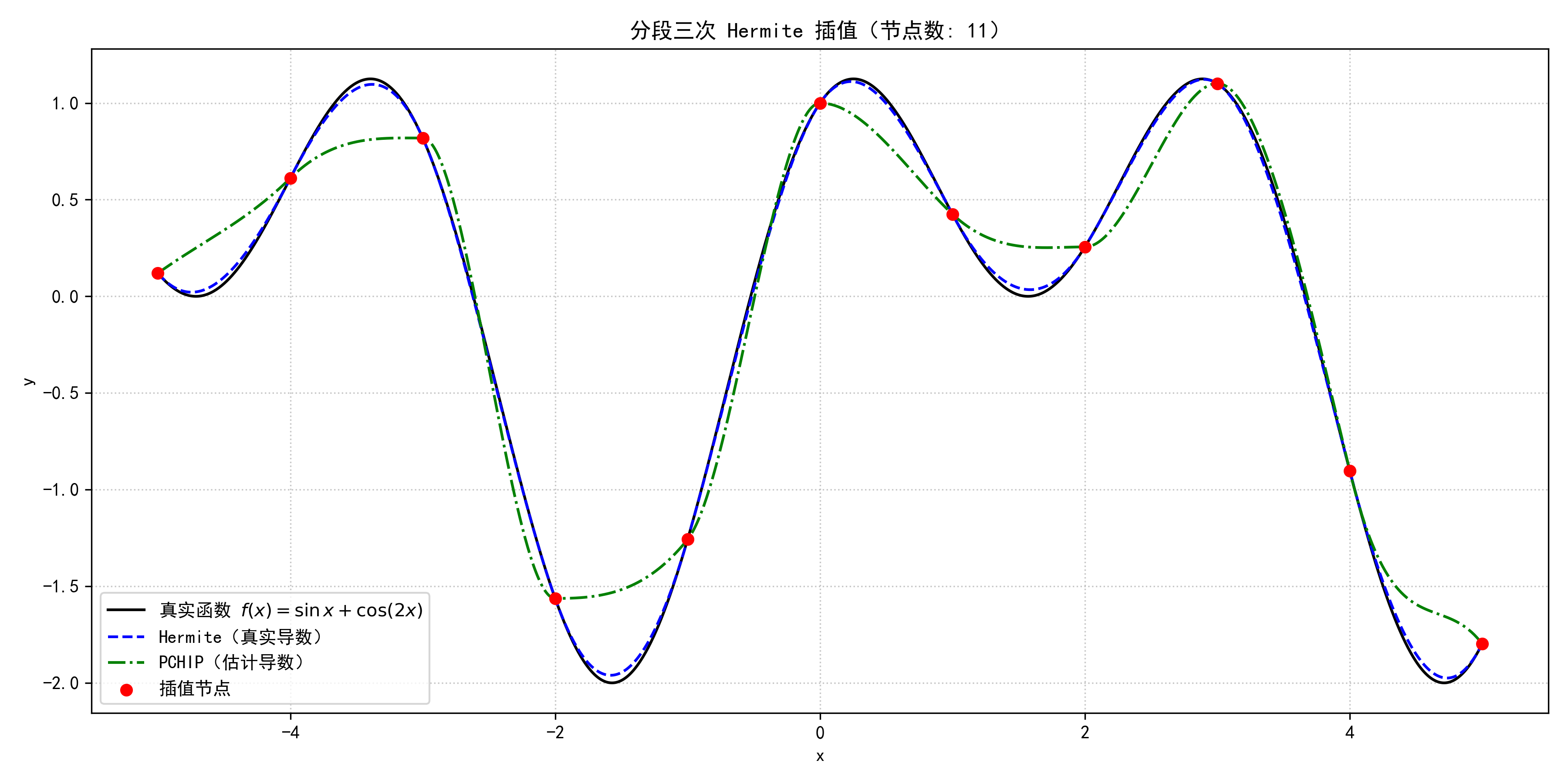
附:文章说明
本文仅为个人理解,若有不当之处,欢迎指正~
